Бифуркационная диаграмма

Определение

Определение 1. Бифуркационной диаграммой динамической системы называется разбиение пространства параметров на максимальные связные подмножества, которые определяются соотношениями топологической эквивалентности и рассматриваются вместе с фазовыми портретами для каждого элемента разбиения.

Смысл

\begin{gather*} \begin{cases} \dot{u}_1=f(u), ~ u \in \mathbb{R} \\ \dot{v}_2=g(v), ~ v \in \mathbb{R}. \end{cases} \end{gather*}

Зафиксируем некоторое значение вектора параметров $ a = a_0 $ и рассмотрим в пространстве параметров максимальное связное множество, содержащее $ a_0, $ такое, что во всех его точках вышеприведённая система топологически эквивалентна этой же системе при $ a = a_0. $ Рассматривая такие множества в пространстве параметров, получим так называемый параметрический портрет вышеприведённой системы. Параметрический портрет вместе с характерными для каждого множества параметров фазовыми портретами составляют бифуркационную диаграмму. При качественном анализе динамической системы желательно получить ее би- фуркационную диаграмму, так как в ней в сжатом виде содержатся все возможные модели поведения данной системы.

Примеры бифуркационных диаграмм

Пример.

Пусть задана динамическая система:

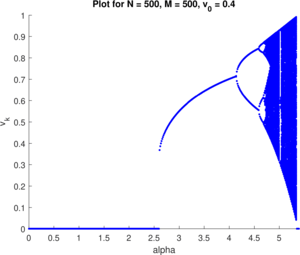
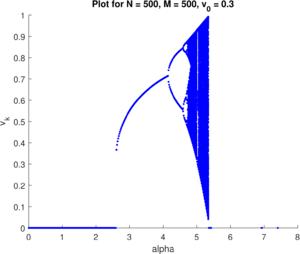
\begin{gather*} \dot{v_{t+1}}_2= \alpha {v_t}^{\frac{3}{2}} (1 - v_t). \end{gather*} Тогда бифуркационные диаграммы выглядят так:

Список литературы

1. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.