Дискретные системы с запаздыванием: различия между версиями
Ksenia23 (обсуждение | вклад) |
Ksenia23 (обсуждение | вклад) |
||
| (не показано 10 промежуточных версий этого же участника) | |||
| Строка 9: | Строка 9: | ||
| − | Для определения системы необходимо | + | Для определения конкретной траектории системы необходимо задать начальные значения: $$u_{0}, u_{1}, ..., u_{T}$$. |
| − | |||
== Преобразование модели == | == Преобразование модели == | ||
| Строка 34: | Строка 33: | ||
== Неподвижная точка системы с запаздыванием == | == Неподвижная точка системы с запаздыванием == | ||
| − | Неподвижной точкой системы с запаздыванием называются решения | + | [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B Неподвижной точкой] $$(v_{1}, ..., v_{T+1}) = (v^{*}, ..., v^{*})$$ системы с запаздыванием называются решения уравнения |
\begin{equation*} | \begin{equation*} | ||
| − | v^{*} = f(v^{*}, ..., v^{*}), v^{*} \in \mathbb{R} | + | v^{*} = f(v^{*}, ..., v^{*}), v^{*} \in \mathbb{R}. |
\end{equation*} | \end{equation*} | ||
| Строка 55: | Строка 54: | ||
\end{equation*} | \end{equation*} | ||
| − | '''Теорема 1.''' Характеристический многочлен матрицы $$ | + | '''Теорема 1.''' Характеристический многочлен матрицы $$A$$ имеет вид |
| − | $$\sum\limits_{i = 0}^{ | + | $$\sum\limits_{i = 0}^{T} a_{1(i+1)} \lambda^{T-i} - \lambda^{T+1} = 0.$$ |
''Доказательство.'' $$\\$$ | ''Доказательство.'' $$\\$$ | ||
| Строка 90: | Строка 89: | ||
Раскладывая матрицу по последнему столбцу: | Раскладывая матрицу по последнему столбцу: | ||
\begin{equation*} | \begin{equation*} | ||
| − | \vert A - \lambda E \vert = -\lambda \vert A_{n} - \lambda E \vert + a_{1(n+1)}\cdot 1 | + | \vert A - \lambda E \vert = -\lambda \vert A_{n} - \lambda E \vert + a_{1(n+1)}\cdot 1 = \sum\limits_{i = 0}^{n} a_{1(i+1)} \lambda^{n-i} - \lambda^{n+1}. |
\end{equation*} | \end{equation*} | ||
| + | Таким образом, шаг индукции доказан. | ||
$$\blacksquare$$ | $$\blacksquare$$ | ||
| Строка 101: | Строка 101: | ||
=== Обобщенная система Рикера === | === Обобщенная система Рикера === | ||
| + | Пусть численность популяции определяется уравнением Рикера с запаздыванием: | ||
\begin{equation*} | \begin{equation*} | ||
u_{t+1} = u_{t} e^{r(1 - u_{t-1})}, r > 0. | u_{t+1} = u_{t} e^{r(1 - u_{t-1})}, r > 0. | ||
\end{equation*} | \end{equation*} | ||
| + | В этом случае рассматривается относительная численность, так как используется отношение действительной численности и максимально возможной для данной экологической системы. | ||
Данное уравнение можно переписать в следующем виде: | Данное уравнение можно переписать в следующем виде: | ||
| Строка 122: | Строка 124: | ||
Найдем матрицу $$A$$ для данной модели: | Найдем матрицу $$A$$ для данной модели: | ||
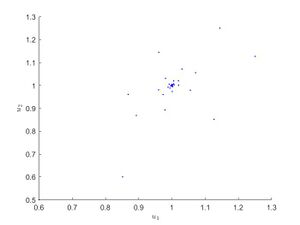
| − | [[Файл:Stable.jpg|мини|Устойчивая неподвижная точка при $$r = 0.7.$$ ]] | + | [[Файл:Stable.jpg|мини|Устойчивая неподвижная точка системы при значении параметра $$r = 0.7 < 1$$. Точки сосредотачиваются около $$(1; 1)$$. ]] |
\begin{equation*} | \begin{equation*} | ||
A = \left( | A = \left( | ||
| Строка 143: | Строка 145: | ||
\end{equation*} | \end{equation*} | ||
| − | Характеристический многочлен данной матрицы равен $$\lambda(e^{r} - \lambda) = 0 \leftrightarrow \lambda_{1} = 0, \lambda_{2} = e^{r}.$$ Так как $$\lambda_{2} \ | + | Характеристический многочлен данной матрицы равен $$\lambda(e^{r} - \lambda) = 0 \leftrightarrow \lambda_{1} = 0, \lambda_{2} = e^{r}.$$ Так как $$\lambda_{2} \geqslant 1$$, то точка является неустойчивой. |
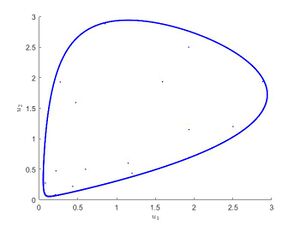
| − | [[Файл:Unstable1.jpg|мини|Неустойчивая неподвижная точка при $$r = 1.3 | + | [[Файл:Unstable1.jpg|мини|Неустойчивая неподвижная точка системы при значении параметра $$r = 1.3 \geqslant 1$$. Точки разбросаны внутри замкнутой кривой.]] |
Аналогично исследуем точку $$v_{2}^{*}$$: | Аналогично исследуем точку $$v_{2}^{*}$$: | ||
| Строка 159: | Строка 161: | ||
\begin{equation*} | \begin{equation*} | ||
| − | \lambda_{1,2} = \dfrac{\pm \sqrt{1-4r} + 1}{2}, r \ | + | \lambda_{1,2} = \dfrac{\pm \sqrt{1-4r} + 1}{2}, r \leqslant \dfrac{1}{4},\\ |
\lambda_{1,2} = \sqrt{r} e^{\pm i \arctan{\sqrt{4r-1}}}, r > \dfrac{1}{4}. | \lambda_{1,2} = \sqrt{r} e^{\pm i \arctan{\sqrt{4r-1}}}, r > \dfrac{1}{4}. | ||
\end{equation*} | \end{equation*} | ||
| − | При $$0< r < \dfrac{1}{4}$$ корни характеристического многочлена вещественны и по модулю меньше $$1$$. Следовательно, точка является устойчивой. Если $$r \ | + | При $$0< r < \dfrac{1}{4}$$ корни характеристического многочлена вещественны и по модулю меньше $$1$$. Следовательно, точка является устойчивой. Если $$r \geqslant \dfrac{1}{4}$$, то корни характеристического многочлена являются комплексно сопряженными числами, причем $$\vert \lambda_{1} \vert \cdot \vert \lambda_{1} \vert = r$$. Тогда при $$\dfrac{1}{4} < r < 1$$ точка устойчива, так как $$\vert \lambda_{1} \vert < 1, \vert \lambda_{2} \vert < 1.$$ При $$r > 1$$ точка является неустойчивой. |
==Список литературы== | ==Список литературы== | ||
Текущая версия на 21:45, 17 октября 2023
Содержание
Модель с запаздыванием
Динамической моделью с дискретным временем с учетом эффекта запаздывания называется модель следующего вида:
\begin{equation*} u_{t+1} = f(u_{t}, u_{t-1}, ..., u_{t - T}), F: \mathbb{R}^{(T+1)} \rightarrow \mathbb{R}, T \in \mathbb{N}, T \geqslant 1. \end{equation*}
Для определения конкретной траектории системы необходимо задать начальные значения: $$u_{0}, u_{1}, ..., u_{T}$$.
Преобразование модели
Модель с запаздыванием можно переписать в виде дискретной системы из $$(T + 1)$$-го уравнения. Для этого введем следующие обозначения: \begin{equation*} v_{1}(t) = u(t), v_{2}(t) = u(t-1), ..., v_{T + 1}(t) = u(t-T). \end{equation*}
Тогда получаем:
\begin{equation*} \begin{cases} v_{1}(t + 1) = f(v_{1}(t), v_{2}(t),..., v_{T+1}(t)),\\ v_{2}(t+1) = v_{1}(t),\\ ...\\ v_{T+1}(t+1) = v_{T}(t). \end{cases} \end{equation*}
Таким образом, системы с запаздыванием являются частным случаем многомерных дискретных систем.
Неподвижная точка системы с запаздыванием
Неподвижной точкой $$(v_{1}, ..., v_{T+1}) = (v^{*}, ..., v^{*})$$ системы с запаздыванием называются решения уравнения \begin{equation*} v^{*} = f(v^{*}, ..., v^{*}), v^{*} \in \mathbb{R}. \end{equation*}
Устойчивость неподвижных точек
Рассмотрим уравнение $$v^{t+ 1} = f(v^{t}_{1}, v^{t}_{2},..., v^{t}_{T+1})$$. Для исследования неподвижных точек удобно воспользоваться линеаризацией и рассмотреть матрицу
\begin{equation*} A = \Vert a_{ij} \Vert_{(T+1)\times (T+1)} = \left( \begin{array}{ccccc} \dfrac{\partial f}{\partial v_{1}} & \dfrac{\partial f}{\partial v_{2}} & \ldots & \dfrac{\partial f}{\partial v_{T}} & \dfrac{\partial f}{\partial v_{T+1}}\\ 1 & 0 & \ldots & 0 & 0\\ 0 & 1 & \ldots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & \ldots & 1 & 0\\ \end{array} \right) \end{equation*}
Теорема 1. Характеристический многочлен матрицы $$A$$ имеет вид $$\sum\limits_{i = 0}^{T} a_{1(i+1)} \lambda^{T-i} - \lambda^{T+1} = 0.$$
Доказательство. $$\\$$ Докажем по индукции. База индукции:
\begin{equation*} A = \left( \begin{array}{cc} a_{11} & a_{12}\\ 1 & 0\\ \end{array} \right) \end{equation*}
\begin{equation*} \left| A - \lambda E \right| = \lambda^{2} - a_{11} \lambda -a_{12} = 0 \Leftrightarrow a_{11} \lambda^{1} + a_{12} \lambda^{0} - \lambda^{2} = 0. \end{equation*}
Сделаем переход от $$n$$ к $$(n+1)$$:
\begin{equation*} \vert A - \lambda E \vert = \left| \begin{array}{ccccc} a_{11} - \lambda & a_{12} & \ldots & a_{1n} & a_{1(n+1)}\\ 1 & -\lambda & \ldots & 0 & 0\\ 0 & 1 & \ldots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots\\ 0 & 0 & \ldots & 1 & -\lambda\\ \end{array} \right| \end{equation*}
Раскладывая матрицу по последнему столбцу: \begin{equation*} \vert A - \lambda E \vert = -\lambda \vert A_{n} - \lambda E \vert + a_{1(n+1)}\cdot 1 = \sum\limits_{i = 0}^{n} a_{1(i+1)} \lambda^{n-i} - \lambda^{n+1}. \end{equation*} Таким образом, шаг индукции доказан.
$$\blacksquare$$
Следствие 1. Собственные значения матрицы $$A$$ являются корнями характеристического многочлена. Если все $$\vert \lambda_{i} \vert < 1$$, то точка является асимптотически устойчивой.
Примеры биологических моделей
Обобщенная система Рикера
Пусть численность популяции определяется уравнением Рикера с запаздыванием: \begin{equation*} u_{t+1} = u_{t} e^{r(1 - u_{t-1})}, r > 0. \end{equation*}
В этом случае рассматривается относительная численность, так как используется отношение действительной численности и максимально возможной для данной экологической системы. Данное уравнение можно переписать в следующем виде:
\begin{equation*} \begin{cases} v_{1}(t+1) = v_{1}(t) e^{r(1 - v_{2}(t))},\\ v_{2}(t+1) = v_{1}(t). \end{cases} \end{equation*}
Неподвижные точки системы определяются из уравнения: \begin{equation*} v^{*} = v^{*} e^{r(1 - v^{*})}. \end{equation*}
Решением данной системы являются точки $$v_{1}^{*} = (0,0), v_{2}^{*} = (1,1).\\$$
Найдем матрицу $$A$$ для данной модели:
\begin{equation*} A = \left( \begin{array}{cc} e^{r(1 - v_{2})} & -rv_{1}v_{2} e^{r(1 - v_{2})}\\ 1 & 0\\ \end{array} \right) \end{equation*}
Подставим $$v_{1}^{*}$$:
\begin{equation*} A = \left( \begin{array}{cc} e^{r} & 0\\ 1 & 0\\ \end{array} \right) \end{equation*}
Характеристический многочлен данной матрицы равен $$\lambda(e^{r} - \lambda) = 0 \leftrightarrow \lambda_{1} = 0, \lambda_{2} = e^{r}.$$ Так как $$\lambda_{2} \geqslant 1$$, то точка является неустойчивой.
Аналогично исследуем точку $$v_{2}^{*}$$:
\begin{equation*} A = \left( \begin{array}{cc} 1 & -r\\ 1 & 0\\ \end{array} \right) \end{equation*}
Характеристический многочлен данной матрицы равен $$-\lambda(1 - \lambda) + r = 0 \leftrightarrow \lambda^{2} - \lambda + r = 0$$. Решением уравнения являются точки:
\begin{equation*} \lambda_{1,2} = \dfrac{\pm \sqrt{1-4r} + 1}{2}, r \leqslant \dfrac{1}{4},\\ \lambda_{1,2} = \sqrt{r} e^{\pm i \arctan{\sqrt{4r-1}}}, r > \dfrac{1}{4}. \end{equation*}
При $$0< r < \dfrac{1}{4}$$ корни характеристического многочлена вещественны и по модулю меньше $$1$$. Следовательно, точка является устойчивой. Если $$r \geqslant \dfrac{1}{4}$$, то корни характеристического многочлена являются комплексно сопряженными числами, причем $$\vert \lambda_{1} \vert \cdot \vert \lambda_{1} \vert = r$$. Тогда при $$\dfrac{1}{4} < r < 1$$ точка устойчива, так как $$\vert \lambda_{1} \vert < 1, \vert \lambda_{2} \vert < 1.$$ При $$r > 1$$ точка является неустойчивой.
Список литературы
1. Братусь А. С., Новожилов А. С., Платонов А. П. Динамические системы и модели биологии. М.: ФИЗМАТЛИТ, 2010.
2. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.