Система Лотки-Вольтерры. Принцип Вольтерры: различия между версиями
Michael23 (обсуждение | вклад) |
Michael23 (обсуждение | вклад) |
||
| Строка 2: | Строка 2: | ||
В данном разделе нами рассматриваются межвидовые отношения типа "хищник - жертва". Опишем формально динамическую систему с непрерывным временем, моделирующую динамику численностей взаимодействующих популяций. Пусть динамика отдельной изолированной популяции задается уравнением: | В данном разделе нами рассматриваются межвидовые отношения типа "хищник - жертва". Опишем формально динамическую систему с непрерывным временем, моделирующую динамику численностей взаимодействующих популяций. Пусть динамика отдельной изолированной популяции задается уравнением: | ||
<math>\dot u = uf(u).</math> | <math>\dot u = uf(u).</math> | ||
| − | Здесь $$u(t)$$ | + | Здесь $$u(t)$$ — численность популяции в момент времени $$t$$, $$f(u)$$ — коэффициент прироста, который зависит от текущей численности. Если имеется несколько взаимодействующих популяций, то коэффициент прироста каждой их них в самой общей ситуации зависит от численностей всех рассматриваемых популяций, и мы получаем систему дифференциальных уравнений: |
\begin{equation}\label{syst1} | \begin{equation}\label{syst1} | ||
\begin{cases} | \begin{cases} | ||
| Строка 11: | Строка 11: | ||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | где $$u = (u_1, u_2, \dots, u_n)$$ | + | где $$u = (u_1, u_2, \dots, u_n)$$ — вектор численностей (или плотностей) взаимодействующих популяций, а $$f(u)$$ — вектор-функция, описывающая систему, каждая компонента которой представляет собой коэффициент прироста соответствующего вида. Динамическую систему \eqref{syst1} будем называть '''системой популяционной динамики''', либо, как на неё часто ссылаются, '''популяционной системой Колмогорова'''. |
== Система Лотки-Вольтерры "хищник-жертва" == | == Система Лотки-Вольтерры "хищник-жертва" == | ||
| − | Одной из первых математических моделей взаимодействующих популяций является система ОДУ, | + | Одной из первых рассмотренных математических моделей взаимодействующих популяций является система ОДУ, именуемая '''моделью Лотки-Вольтерры''' (1925 и 1926 годы соответственно), которая описывает вазимодействие двух видов, один из которых является хищником, а другой — жертвой (например, экологическая система волки-зайцы) |
[[Файл:Заяц-волк.png|обрамить|центр|'''рис.1''' Модель Заяц-Волк попадалась в художественных произведениях уже полвека тому назад]] | [[Файл:Заяц-волк.png|обрамить|центр|'''рис.1''' Модель Заяц-Волк попадалась в художественных произведениях уже полвека тому назад]] | ||
| − | Если $$N(t)$$ | + | Если $$N(t)$$ — численность жертв, $$P(t)$$ — численность хищников в момент времени $$t$$, то модель Лотки-Вольтерры имеет вид: |
\begin{equation}\label{syst2} | \begin{equation}\label{syst2} | ||
| Строка 27: | Строка 27: | ||
\end{equation} | \end{equation} | ||
| − | где a, b, c, d | + | где a, b, c, d — положительные постоянные. |
| − | + | В основу системы \eqref{syst2} положены предположения, характеризующиеся следующими гипотезами: | |
| + | #в отсутствиии хищников жертвы размножаются неограниченно ($$\dot N = aN$$); | ||
| + | #хищники в отсутствии жертв вымирают ($$\dot P = -dP$$); | ||
| + | #слагаемые, пропорциональные NP, рассматриваются как превращение энергии одного источника в энергию другого (эффект влияния популяции хищников на популяцию жертв заключается в уменьшении относительной скорости прироста численности жертв на величину, пропорциональную численности хищников). | ||
| − | + | Так как мы смотрим на систему \eqref{syst2} как на математическую модель взаимодействущих популяций, естественно будет считать фазовым пространством множество $$\mathbb{R}^2_+$$, которое является инвариантным, так как любая траектория, начинающаяся в $$\mathbb{R}^2_+$$ не может пересечь линии $$N = 0$$ и $$P = 0$$, являющиеся фазовыми кривыми. | |
В безразмерных переменных система принимает вид: | В безразмерных переменных система принимает вид: | ||
| Строка 44: | Строка 47: | ||
где: | где: | ||
<math>u(\tau) = \frac{d}{c}N(t), ~v(\tau) = \frac{bP(t)}{a}, ~\tau = at, ~\gamma = \frac{c}{a}.</math> | <math>u(\tau) = \frac{d}{c}N(t), ~v(\tau) = \frac{bP(t)}{a}, ~\tau = at, ~\gamma = \frac{c}{a}.</math> | ||
| − | Система \eqref{syst3} имеет две неподвижные точки: (0,0) | + | Система \eqref{syst3} имеет две неподвижные точки: $$A(0,0)$$ и $$B(1,1)$$. Стандартный линейный анализ показывает, что точка $$A(0,0)$$ - седло, а для $$B(1,1)$$ матрица Якоби имеет вид: |
\begin{equation*} | \begin{equation*} | ||
| − | J = \left( | + | J\vert_{(1,1)}= \left( |
\begin{array}{cc} | \begin{array}{cc} | ||
0 & -1 \\ | 0 & -1 \\ | ||
| Строка 62: | Строка 65: | ||
<math>\frac{dv}{dv} = \gamma\frac{v(u-1)}{u(1-v)}, </math> | <math>\frac{dv}{dv} = \gamma\frac{v(u-1)}{u(1-v)}, </math> | ||
решение которого: | решение которого: | ||
| − | |||
| − | где $$H > H_{min} = 1 + \gamma$$, где $$H_{min}$$ достигается в точке $$u=1, ~v=1$$. Действительно, | + | \begin{equation}\label{eq4} |
| + | \gamma u + v - \ln{u^\gamma v} = H = H(u,v), | ||
| + | \end{equation} | ||
| + | |||
| + | где $$H > H_{min} = 1 + \gamma$$, где $$H_{min}$$ достигается в точке $$u=1, ~v=1$$. | ||
| + | |||
| + | Действительно, | ||
| + | \[H_u(1,1) = 0, ~H_v(1,1) = 0, ~\text{и} ~H_{uu}(1,1) < 0, ~H_{uv}(1,1) = 0, ~H_{vv}(1,1) < 0.\] | ||
| + | Легко проверить, что $$L_tH(u,v) = 0$$, и, следовательно, функция $$H(u,v)$$ задает первый интеграл системы \eqref{syst3}. Анализируя линии уровня фукции $$H(u,v)$$ можно показать, что для любых $$H > H_{min}$$ они являются замкнутыми кривыми (см. '''рис.2'''), в общем случае анализ линий уровня функции $$H(u, v)$$ достаточно сложен. | ||
| + | |||
| + | Если разложить в окрестности точки $$B(1,1)$$ функцию $$H(u, v)$$ в ряд Тейлора, то получим: | ||
<math> H(u,v) = 1 + \gamma + \gamma\frac{(u-1)^2}{2} + \gamma\frac{(v-1)^2}{2} + \o\left((v-1)^2\right) + \o\left((u-1)^2\right).</math> | <math> H(u,v) = 1 + \gamma + \gamma\frac{(u-1)^2}{2} + \gamma\frac{(v-1)^2}{2} + \o\left((v-1)^2\right) + \o\left((u-1)^2\right).</math> | ||
| Строка 70: | Строка 82: | ||
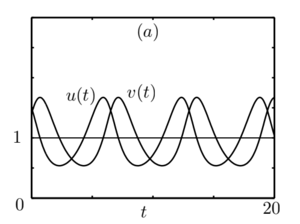
[[Файл:Solution 1.png|мини|'''рис.3''' Решение системы (3), начальные условия взяты близко к положению равновесия.]] | [[Файл:Solution 1.png|мини|'''рис.3''' Решение системы (3), начальные условия взяты близко к положению равновесия.]] | ||
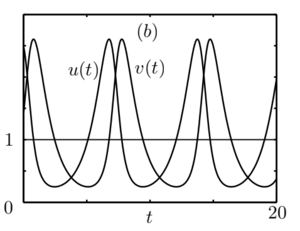
[[Файл:Solution 2.png|мини|'''рис.4''' Решение системы (3), начальные условия взяты далеко от положения равновесия.]] | [[Файл:Solution 2.png|мини|'''рис.4''' Решение системы (3), начальные условия взяты далеко от положения равновесия.]] | ||
| − | Последнее равенство означает, что в окрестности точки $$(1, 1)$$ существует обратимая дифференцируемая замена переменных, которая переводит $$H(u,v)$$ в функцию: | + | Последнее равенство означает, что в окрестности точки $$B(1,1)$$ существует обратимая дифференцируемая замена переменных, которая переводит $$H(u,v)$$ в функцию: |
<math> G(u,v) = 1 + \gamma + \frac{(x-1)^2}{2} + \frac{(y-1)^2}{2},</math> | <math> G(u,v) = 1 + \gamma + \frac{(x-1)^2}{2} + \frac{(y-1)^2}{2},</math> | ||
линии уровня которой - окружности. Следовательно, по крайней мере в окрестности точки $$(1,1)$$ линии уровня иисходной функции $$H(u,v)$$ представляют собой замкнутые кривые. Замкнутые фазовые траектории на плоскости $$u,~v$$ отвечают периодическим решениям системы \eqref{syst3}. Начальные условия $$u(0) = u_0, ~v(0) = v_0$$ определяют константу H в выражении \eqref{eq4}. Типичные решения системы \eqref{syst3} приведены на '''рис.3''' и '''рис.4'''. | линии уровня которой - окружности. Следовательно, по крайней мере в окрестности точки $$(1,1)$$ линии уровня иисходной функции $$H(u,v)$$ представляют собой замкнутые кривые. Замкнутые фазовые траектории на плоскости $$u,~v$$ отвечают периодическим решениям системы \eqref{syst3}. Начальные условия $$u(0) = u_0, ~v(0) = v_0$$ определяют константу H в выражении \eqref{eq4}. Типичные решения системы \eqref{syst3} приведены на '''рис.3''' и '''рис.4'''. | ||
| − | + | Главным же недостатком системы \eqref{syst3} как математической модели экологической системы принято считать её '''структурную неустойчивость''': малое изменение правых частей \eqref{syst3} в метрике соответствующего пространства функций может приводить к качественному изменению поведения решений. | |
| − | + | Одой из причин того, что система \eqref{syst3} является структурно неустойчивой, является существование первого интеграла. Системы, обладающие первым интегралом, называются '''консервативными''', и в силу своей структурной неустойчивости редко используются в качестве математических моделей такого рода. Считается, что первые интегралы таких систем описывают некоторые «законы сохранения». | |
| − | + | Изучение консервативности динамической системы неразделимо со свойством сохранения фазового объема. Любая консервативная система сохраняет фазовый объем (быть может после умножения правых частей на общий скалярный множитель). | |
| − | |||
| − | |||
Сделав замену переменных $$u = \ln{N}, ~v = \ln{P}$$ в системе \eqref{syst2}, получим: | Сделав замену переменных $$u = \ln{N}, ~v = \ln{P}$$ в системе \eqref{syst2}, получим: | ||
\begin{equation}\label{syst5} | \begin{equation}\label{syst5} | ||
| Строка 90: | Строка 100: | ||
\end{equation} | \end{equation} | ||
| − | + | Можно проверить, что для правых частей системы выполняется условие $$\div{f} = 0$$, т.е. система Лотки-Вольтерры сохраняет фазовый объем в $$\mathbb{R}^2_+$$. | |
| − | |||
| − | |||
| − | |||
'''Утверждение 1 '''(Принцип Вольтерры) Если в системе хищник–жертва, описываемой моделью \eqref{syst2}, оба вида истребляются равномерно и пропорционально числу их индивидуумов, то среднее число жертв возрастает, а среднее число хищников убывает. | '''Утверждение 1 '''(Принцип Вольтерры) Если в системе хищник–жертва, описываемой моделью \eqref{syst2}, оба вида истребляются равномерно и пропорционально числу их индивидуумов, то среднее число жертв возрастает, а среднее число хищников убывает. | ||
| Строка 105: | Строка 112: | ||
так как $$N(T) = N(0), ~P(T) = P(0)$$. То есть среднее число жертв и хищников остается постоянным и равным координатам нетривиального положения равновесия \eqref{syst2}. | так как $$N(T) = N(0), ~P(T) = P(0)$$. То есть среднее число жертв и хищников остается постоянным и равным координатам нетривиального положения равновесия \eqref{syst2}. | ||
| − | Если оба вида истребляются равномерно и пропорционально числу их индивидуумов, то у жертв уменьшается коэффициент рождаемости $$a$$, который становится равным $$a - \delta_2$$, а у хищников увеличивается коэффциент смертности $$d$$, который становится равен $$d+\delta_1$$, другими словами, среднее число жертв равно $$\frac{d+\delta_1}{c}$$, а среднее число хищников | + | Если оба вида истребляются равномерно и пропорционально числу их индивидуумов, то у жертв уменьшается коэффициент рождаемости $$a$$, который становится равным $$a - \delta_2$$, а у хищников увеличивается коэффциент смертности $$d$$, который становится равен $$d+\delta_1$$, другими словами, среднее число жертв равно $$\frac{d+\delta_1}{c}$$, а среднее число хищников — $$\frac{a-\delta_2}{b}$$.<math>\blacksquare</math> |
Описанный выше эффект наблюдается в природе. Например, во время первой мировой войны лов рыбы в Адриатическом море был сильно сокращен, что, к удивлению биологов, привело к увеличению числа хищников и уменьшению числа жертв (указанный факт стал одним из побудительных мотивов записать и проанализировать модель \eqref{syst2}). Кроме всего прочего, принцип Вольтерры показывает двойственный характер применения средств от насекомых (инсектицидов) для сохранения урожая на полях. Почти все такие химические вещества действуют не только на вредителей, но и на их естественных врагов, что зачастую приводит к увеличению числа вредителей и уменьшению, например, числа птиц, питающихся этими вредителями. Отметим также, что принцип Вольтерры впервые теоретически показал, что в экосистеме "хищник–жертва" популяция жертв более чувствительна к процессу пропорционального уменьшения особей в популяции. | Описанный выше эффект наблюдается в природе. Например, во время первой мировой войны лов рыбы в Адриатическом море был сильно сокращен, что, к удивлению биологов, привело к увеличению числа хищников и уменьшению числа жертв (указанный факт стал одним из побудительных мотивов записать и проанализировать модель \eqref{syst2}). Кроме всего прочего, принцип Вольтерры показывает двойственный характер применения средств от насекомых (инсектицидов) для сохранения урожая на полях. Почти все такие химические вещества действуют не только на вредителей, но и на их естественных врагов, что зачастую приводит к увеличению числа вредителей и уменьшению, например, числа птиц, питающихся этими вредителями. Отметим также, что принцип Вольтерры впервые теоретически показал, что в экосистеме "хищник–жертва" популяция жертв более чувствительна к процессу пропорционального уменьшения особей в популяции. | ||
Версия 16:34, 13 декабря 2023
Популяционная система Коломогорова
В данном разделе нами рассматриваются межвидовые отношения типа "хищник - жертва". Опишем формально динамическую систему с непрерывным временем, моделирующую динамику численностей взаимодействующих популяций. Пусть динамика отдельной изолированной популяции задается уравнением\[\dot u = uf(u).\] Здесь $$u(t)$$ — численность популяции в момент времени $$t$$, $$f(u)$$ — коэффициент прироста, который зависит от текущей численности. Если имеется несколько взаимодействующих популяций, то коэффициент прироста каждой их них в самой общей ситуации зависит от численностей всех рассматриваемых популяций, и мы получаем систему дифференциальных уравнений: \begin{equation}\label{syst1} \begin{cases} \dot u_1 = u_1f_1(u_1, u_2, \dots, u_n),\\ \dot u_2 = u_2f_2(u_1, u_2, \dots, u_n),\\ \dots\\ \dot u_n = u_nf_n(u_1, u_2, \dots, u_n),\\ \end{cases} \end{equation} где $$u = (u_1, u_2, \dots, u_n)$$ — вектор численностей (или плотностей) взаимодействующих популяций, а $$f(u)$$ — вектор-функция, описывающая систему, каждая компонента которой представляет собой коэффициент прироста соответствующего вида. Динамическую систему \eqref{syst1} будем называть системой популяционной динамики, либо, как на неё часто ссылаются, популяционной системой Колмогорова.
Система Лотки-Вольтерры "хищник-жертва"
Одной из первых рассмотренных математических моделей взаимодействующих популяций является система ОДУ, именуемая моделью Лотки-Вольтерры (1925 и 1926 годы соответственно), которая описывает вазимодействие двух видов, один из которых является хищником, а другой — жертвой (например, экологическая система волки-зайцы)
Если $$N(t)$$ — численность жертв, $$P(t)$$ — численность хищников в момент времени $$t$$, то модель Лотки-Вольтерры имеет вид:
\begin{equation}\label{syst2} \begin{cases} \dot N = aN - bNP,\\ \dot P = -dP + cNP,\\ \end{cases} \end{equation}
где a, b, c, d — положительные постоянные.
В основу системы \eqref{syst2} положены предположения, характеризующиеся следующими гипотезами:
- в отсутствиии хищников жертвы размножаются неограниченно ($$\dot N = aN$$);
- хищники в отсутствии жертв вымирают ($$\dot P = -dP$$);
- слагаемые, пропорциональные NP, рассматриваются как превращение энергии одного источника в энергию другого (эффект влияния популяции хищников на популяцию жертв заключается в уменьшении относительной скорости прироста численности жертв на величину, пропорциональную численности хищников).
Так как мы смотрим на систему \eqref{syst2} как на математическую модель взаимодействущих популяций, естественно будет считать фазовым пространством множество $$\mathbb{R}^2_+$$, которое является инвариантным, так как любая траектория, начинающаяся в $$\mathbb{R}^2_+$$ не может пересечь линии $$N = 0$$ и $$P = 0$$, являющиеся фазовыми кривыми.
В безразмерных переменных система принимает вид:
\begin{equation}\label{syst3} \begin{cases} \dot u = u(1-v),\\ \dot v = \gamma v(u-1),\\ \end{cases} \end{equation}
где\[u(\tau) = \frac{d}{c}N(t), ~v(\tau) = \frac{bP(t)}{a}, ~\tau = at, ~\gamma = \frac{c}{a}.\] Система \eqref{syst3} имеет две неподвижные точки: $$A(0,0)$$ и $$B(1,1)$$. Стандартный линейный анализ показывает, что точка $$A(0,0)$$ - седло, а для $$B(1,1)$$ матрица Якоби имеет вид:
\begin{equation*} J\vert_{(1,1)}= \left( \begin{array}{cc} 0 & -1 \\ \gamma & 0 \end{array} \right) \end{equation*}
а её собственные значения $$\lambda_{1,2} = \pm i \sqrt{\gamma}.$$ Другими словами, положение равновесия (1,1) негиперболическое, и линейный анализ не позволяет сделать вывод об его устойчивости.
Фазовые кривые системы \eqref{syst3} являются интегральными кривыми уравнения\[\frac{dv}{dv} = \gamma\frac{v(u-1)}{u(1-v)}, \] решение которого:
\begin{equation}\label{eq4} \gamma u + v - \ln{u^\gamma v} = H = H(u,v), \end{equation}
где $$H > H_{min} = 1 + \gamma$$, где $$H_{min}$$ достигается в точке $$u=1, ~v=1$$.
Действительно, \[H_u(1,1) = 0, ~H_v(1,1) = 0, ~\text{и} ~H_{uu}(1,1) < 0, ~H_{uv}(1,1) = 0, ~H_{vv}(1,1) < 0.\] Легко проверить, что $$L_tH(u,v) = 0$$, и, следовательно, функция $$H(u,v)$$ задает первый интеграл системы \eqref{syst3}. Анализируя линии уровня фукции $$H(u,v)$$ можно показать, что для любых $$H > H_{min}$$ они являются замкнутыми кривыми (см. рис.2), в общем случае анализ линий уровня функции $$H(u, v)$$ достаточно сложен.
Если разложить в окрестности точки $$B(1,1)$$ функцию $$H(u, v)$$ в ряд Тейлора, то получим\[ H(u,v) = 1 + \gamma + \gamma\frac{(u-1)^2}{2} + \gamma\frac{(v-1)^2}{2} + \o\left((v-1)^2\right) + \o\left((u-1)^2\right).\]
Последнее равенство означает, что в окрестности точки $$B(1,1)$$ существует обратимая дифференцируемая замена переменных, которая переводит $$H(u,v)$$ в функцию\[ G(u,v) = 1 + \gamma + \frac{(x-1)^2}{2} + \frac{(y-1)^2}{2},\] линии уровня которой - окружности. Следовательно, по крайней мере в окрестности точки $$(1,1)$$ линии уровня иисходной функции $$H(u,v)$$ представляют собой замкнутые кривые. Замкнутые фазовые траектории на плоскости $$u,~v$$ отвечают периодическим решениям системы \eqref{syst3}. Начальные условия $$u(0) = u_0, ~v(0) = v_0$$ определяют константу H в выражении \eqref{eq4}. Типичные решения системы \eqref{syst3} приведены на рис.3 и рис.4.
Главным же недостатком системы \eqref{syst3} как математической модели экологической системы принято считать её структурную неустойчивость: малое изменение правых частей \eqref{syst3} в метрике соответствующего пространства функций может приводить к качественному изменению поведения решений.
Одой из причин того, что система \eqref{syst3} является структурно неустойчивой, является существование первого интеграла. Системы, обладающие первым интегралом, называются консервативными, и в силу своей структурной неустойчивости редко используются в качестве математических моделей такого рода. Считается, что первые интегралы таких систем описывают некоторые «законы сохранения».
Изучение консервативности динамической системы неразделимо со свойством сохранения фазового объема. Любая консервативная система сохраняет фазовый объем (быть может после умножения правых частей на общий скалярный множитель). Сделав замену переменных $$u = \ln{N}, ~v = \ln{P}$$ в системе \eqref{syst2}, получим: \begin{equation}\label{syst5} \begin{cases} \dot u = a - be^v,\\ \dot v = -d + ce^u.\\ \end{cases} \end{equation}
Можно проверить, что для правых частей системы выполняется условие $$\div{f} = 0$$, т.е. система Лотки-Вольтерры сохраняет фазовый объем в $$\mathbb{R}^2_+$$.
Утверждение 1 (Принцип Вольтерры) Если в системе хищник–жертва, описываемой моделью \eqref{syst2}, оба вида истребляются равномерно и пропорционально числу их индивидуумов, то среднее число жертв возрастает, а среднее число хищников убывает.
Доказательство. Пусть $$N(t), ~P(t)$$ — периодические решения системы \eqref{syst2} с периодом $$T$$. Из \eqref{syst2} следует, что\[ \frac{d}{dt}\ln{N} = a - bP, \quad \frac{d}{dt}\ln{P} = -d + cN.\]
Интегрируя последние равенства по $$t$$ в промежутке от $$0$$ до $$T$$, получим\[ \frac{1}{T}\int_{0}^{T} P(t)dt= \frac{a}{b}, \quad \frac{1}{T}\int_{0}^{T} N(t)dt= \frac{d}{c},\]
так как $$N(T) = N(0), ~P(T) = P(0)$$. То есть среднее число жертв и хищников остается постоянным и равным координатам нетривиального положения равновесия \eqref{syst2}.
Если оба вида истребляются равномерно и пропорционально числу их индивидуумов, то у жертв уменьшается коэффициент рождаемости $$a$$, который становится равным $$a - \delta_2$$, а у хищников увеличивается коэффциент смертности $$d$$, который становится равен $$d+\delta_1$$, другими словами, среднее число жертв равно $$\frac{d+\delta_1}{c}$$, а среднее число хищников — $$\frac{a-\delta_2}{b}$$.\(\blacksquare\)
Описанный выше эффект наблюдается в природе. Например, во время первой мировой войны лов рыбы в Адриатическом море был сильно сокращен, что, к удивлению биологов, привело к увеличению числа хищников и уменьшению числа жертв (указанный факт стал одним из побудительных мотивов записать и проанализировать модель \eqref{syst2}). Кроме всего прочего, принцип Вольтерры показывает двойственный характер применения средств от насекомых (инсектицидов) для сохранения урожая на полях. Почти все такие химические вещества действуют не только на вредителей, но и на их естественных врагов, что зачастую приводит к увеличению числа вредителей и уменьшению, например, числа птиц, питающихся этими вредителями. Отметим также, что принцип Вольтерры впервые теоретически показал, что в экосистеме "хищник–жертва" популяция жертв более чувствительна к процессу пропорционального уменьшения особей в популяции.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.