Неподвижные точки системы: различия между версиями
Kirich23 (обсуждение | вклад) |
Kirich23 (обсуждение | вклад) |
||
| (не показано 127 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | ==Случай динамических систем с дискретным временем== |
| − | Пусть задана динамическая система | + | |
| + | Пусть задана динамическая система: | ||
\begin{equation} \label{sist1} | \begin{equation} \label{sist1} | ||
| − | + | u_{t+1} = f(u_t), u_{t=0}=u_0,\ u_t \in \mathbb{R}^n,\ f : \mathbb{R}^n → \mathbb{R}^n. | |
\end{equation} | \end{equation} | ||
'''Определение 1.''' | '''Определение 1.''' | ||
| − | + | '''Неподвижными точками''' | |
| − | + | [https://sawiki.cs.msu.ru/index.php/%D0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0 динамической системы] | |
| + | (\ref{sist1}) называются такие точки пространства состояний $$u^{∗}$$, что $$f(u^{∗}) = u^{∗}$$. | ||
| + | |||
| + | Кроме термина ''неподвижная точка'' используют иногда термины ''стационарная точка'' или ''положение равновесия''. | ||
| − | + | ===Устойчивость неподвижных точек=== | |
| − | |||
| − | + | Реальная система подвержена внешним воздействиям, она не может находиться все время в одном и том же состоянии. | |
| − | + | Если немного возмутить состояние системы так, что | |
| − | + | ее состояние окажется в некоторой окрестности положения равновесия, то возможны следующие сценарии: траектории | |
| + | могут покинуть эту окрестность, остаться в этой окрестности, или приблизиться к | ||
| + | положению равновесия. Естественно назвать положение равновесия ''неустойчивым'' | ||
| + | в первом случае и ''устойчивым'' в двух других. | ||
'''Определение 2.''' | '''Определение 2.''' | ||
| − | Неподвижная точка $$ | + | Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется '''устойчивой по Ляпунову''', |
| − | для любых начальных данных $$ | + | если для любого $$\varepsilon > 0$$ существует такое $$\delta > 0$$, |
| + | что для любых начальных данных $$u(t_0)$$ из $$\delta$$-окрестности точки $$u^{*}$$ вся траектория системы $$u(t)$$ | ||
| + | содержится в $$\varepsilon$$-окрестности точки $$u^{*}$$. | ||
| − | + | $$\forall \varepsilon > 0 ~ \exists \delta(\varepsilon)>0 ~ \forall u(t_0) \in \mathcal{U}_{\delta}(u^{*})$$, $$|u^{*}-u(t)|< \varepsilon, ~\forall t \geqslant t_0$$. | |
| − | ''' | + | '''Определение 3.''' |
| − | $$ | + | Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется '''асимптотически устойчивой''', если она является |
| + | устойчивой по Ляпунову и $$\displaystyle{\lim_{t\to\infty}} u(t) = u^{*}$$. | ||
| − | Если | + | Если положение равновесия не является ''устойчивым'', то говорят, что оно ''неустойчиво''. |
| − | Асимптотически устойчивые неподвижные точки иногда называют аттракторами, а неустойчивые неподвижные точки иногда называют репеллерами. | + | Асимптотически устойчивые неподвижные точки иногда называют |
| + | [https://ru.wikipedia.org/wiki/%D0%90%D1%82%D1%82%D1%80%D0%B0%D0%BA%D1%82%D0%BE%D1%80 ''аттракторами''], | ||
| + | а неустойчивые неподвижные точки иногда называют ''репеллерами''. | ||
'''Теорема 1.''' | '''Теорема 1.''' | ||
| − | Пусть $$ | + | Пусть $$u^{*}$$ — неподвижная точка отображения (\ref{sist1}), т.е. $$u^{*}$$ = $$f(u^{*})$$, и пусть $$f$$ [https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%B8%D0%BC%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F обратима] |
| − | $$|f^{'}( | + | в малой окрестности $$u^{*}$$. Тогда $$u^{*}$$ асимптотически устойчива, если |
| + | $$|f^{'}(u^{*})| < 1$$, | ||
и неустойчива, если | и неустойчива, если | ||
| − | $$|f^{'}( | + | $$|f^{'}(u^{*})| > 1$$. |
| − | Если $$ |f^{'}( | + | Если $$ |f^{'}(u^{*})| = 1$$, то требуются дополнительные исследования. |
| − | ''Доказательство | + | '''Доказательство:''' |
| − | Пусть $$|f^{'}( | + | Пусть $$|f^{'}(u^{*})| < 1$$ и пусть $$u$$ принадлежит малой окрестности $$u^{*}$$. |
Так как | Так как | ||
\[ | \[ | ||
| − | \displaystyle{\lim_{t\to\infty}} \frac{|f( | + | \displaystyle{\lim_{t\to\infty}} \frac{|f(u)-f(u^{*})|}{|u-u^{*}|}=|f^{'}(u^{*})|, |
\] | \] | ||
| − | поэтому существует такая окрестность $$ | + | поэтому существует такая окрестность $$u^{*}$$, что |
\[ | \[ | ||
| − | \frac{|f( | + | \frac{|f(u)-f(u^{*})|}{|u-u^{*}|} \leqslant a, |
\] | \] | ||
| − | для всех $$ | + | для всех $$u$$ из этой окрестности; здесь $$a$$ — некоторое число, такое что $$|f^{'}(u^{*})| \leqslant a < 1$$. |
| − | Таким образом, $$f( | + | Таким образом, $$f(u)$$ остается в той же окрестности, что и $$u$$, и, кроме того, ближе к |
| − | неподвижной точке $$ | + | неподвижной точке $$u^{*}$$, по крайней мере, на множитель $$a$$. Отсюда следует, что |
| − | \[|f(f( | + | \[|f(f(u)) − f(f(u^{*}))| \leqslant a |f(u) − f(u^{*})| \leqslant a^2|u − u^{*}|, |
\] | \] | ||
или, по индукции, | или, по индукции, | ||
| − | \[|f^{k}( | + | \[|f^{k}(u) − u^{*}| \leqslant a^{k}|u − u^{*}|, |
\] | \] | ||
| − | где $$f^{k}$$ обозначает $$k$$-ую суперпозицию отображения $$f$$. Таким образом мы доказали,что последовательность $$f^{k}( | + | где $$f^{k}$$ обозначает $$k$$-ую суперпозицию отображения $$f$$. Таким образом мы доказали, что последовательность $$f^{k}(u)$$ будет сходиться к $$u^{*}$$, то есть является асимптотически устойчивой. |
Вторая часть утверждения доказывается сходным образом. | Вторая часть утверждения доказывается сходным образом. | ||
$$\blacksquare$$ | $$\blacksquare$$ | ||
| − | == Пример поиска неподвижных точек с помощью графического метода == | + | ===Пример поиска неподвижных точек с помощью графического метода=== |
| − | |||
| − | |||
| − | |||
Пусть задана система $$v_{t+1} = \frac{r v_t}{(1+ v_t)^b}$$. | Пусть задана система $$v_{t+1} = \frac{r v_t}{(1+ v_t)^b}$$. | ||
| − | Графически неподвижные точки — это точки пересечения графика функции $$f( | + | Графически неподвижные точки — это точки пересечения графика функции $$f(v)$$ и биссектрисы первого координатного угла |
| − | $$ | + | $$v_{t+1} = v_{t}$$ (нас интересуют только неотрицательные решения). |
Для нахождения неподвижных точек заданной системы рассмотрим возможные пересечения графика функции $$f(v)=\frac{rv}{(1+v)^b}$$ с прямой $$g(v)=v$$. | Для нахождения неподвижных точек заданной системы рассмотрим возможные пересечения графика функции $$f(v)=\frac{rv}{(1+v)^b}$$ с прямой $$g(v)=v$$. | ||
| Строка 82: | Строка 91: | ||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | при любых $$v \geqslant 0, ~r,b > 0$$ имеет хотя бы один корень, а именно $$v=0$$. Второй корень $$v=r^{1/b}-1$$ система может иметь только при значении параметра $$r> 1$$. Больше двух неотрицательных корней система (\ref{sist2}) не имеет. | + | при любых $$v \geqslant 0, ~r,b > 0$$ имеет хотя бы один корень, а именно $$v=0$$. Второй корень $$v=r^{1/b}-1$$ система может иметь только при значении параметра $$r>1$$. Больше двух неотрицательных корней система (\ref{sist2}) не имеет. |
| + | [[Файл:mergedstaticpoints1.png|мини|центр|750px|$$r=30, b=3$$, система имеет два различных неотрицательных корня. $$r=0.9, b=7$$, система имеет единственный корень $$v=0$$.]] | ||
| − | + | ===Пример исследования неподвижных точек на устойчивость=== | |
| − | |||
| − | == | + | Исследуем на устойчивость неподвижные точки $$v^{*}=r^{1/b}-1$$ и $$v^{*}=0$$ для системы (\ref{sist2}). |
| − | + | \[ | |
| − | |||
| − | |||
f_v(v^{*})=\frac{r((1+v)^b-bv(1+v)^{b-1})}{(1+v)^{2b}}. | f_v(v^{*})=\frac{r((1+v)^b-bv(1+v)^{b-1})}{(1+v)^{2b}}. | ||
| − | \ | + | \] |
| − | ''' | + | '''1. Исследование первой точки $$v^{*}=r^{1/b}-1$$:''' |
| − | Подставим $$ | + | Подставим $$v^{*}=r^{1/b}-1$$ в выражение (\ref{sist2}) и с учетом наложенных ограничений $$r>1, b>0$$ для существования точки получим |
\[ | \[ | ||
| − | f_v( | + | f_v(v^{*})=b(r^{-1/b}-1)+1. |
\] | \] | ||
| − | Согласно теореме 1 точка $$v^{*} | + | Согласно теореме 1 точка $$v^{*}=r^{1/b}-1$$ будет: |
| + | |||
| + | ''Асимптотически устойчивой'', при $$r^{-1/b}<1$$. | ||
| + | |||
| + | ''Неустойчивой'', при $$r^{-1/b}>1$$. | ||
| + | |||
| + | Отметим, что точка $$v^{*}=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, | ||
| + | таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, | ||
| + | точка $$v^{*}=r^{1/b}-1$$ ''асимптотически устойчива'' всегда, если она существует. | ||
| + | |||
| + | [[Файл:mergedstaticpoints2.png|мини|центр|750px|''Аттрактор'' в точке $$v^{*}=r^{1/b}-1$$ при параметрах $$r=10, b=2, v_0=1$$. ''Аттрактор'' в точке $$v^{*}=r^{1/b}-1$$ при параметрах $$r=3, b=0.9, v_0=4.5$$.]] | ||
| − | ''' | + | '''2. Исследование второй точки $$v^{*}=0$$:''' |
| − | Подставим $$ | + | Подставим $$v^{*}=0$$ в выражение (\ref{sist2}) и получим |
\[ | \[ | ||
| − | f_v( | + | f_v(v^{*})=r. |
\] | \] | ||
| − | Таким образом, по теореме 1, точка $$v^{*} | + | Таким образом, по теореме 1, точка $$v^{*}=0$$ будет: |
| − | + | ''Асимптотически устойчивой'', при $$r<1$$. | |
| − | ''' | + | ''Неустойчивой'', при $$r>1$$. |
| − | + | [[Файл:mergedstaticpoints3.png|мини|центр|750px|''Аттрактор'' в точке $$v^*=0$$ при параметрах $$r=0.9, b=0.7, v_0=4.$$ ''Репеллер'' в точке $$v^*=0$$ при параметрах $$r=2, b=0.9, v_0=2.$$]] | |
| − | Пусть задана динамическая система | + | ==Случай динамических систем с непрерывным временем== |
| + | Пусть задана динамическая система: | ||
| − | \begin{equation} \label{ | + | \begin{equation} \label{sistnepr} |
| − | \dot u=f(u), u \in U \subseteq \mathbb{R}^ | + | \dot{u} = f(u),\ u \in U \subseteq \mathbb{R}^n,\ f : U → \mathbb{R}^n. |
\end{equation} | \end{equation} | ||
'''Определение 4.''' | '''Определение 4.''' | ||
| − | + | '''Неподвижными точками''' | |
| − | + | [https://sawiki.cs.msu.ru/index.php/%D0%94%D0%B8%D0%BD%D0%B0%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0 динамической системы] | |
| − | + | (\ref{sistnepr}) называются такие точки пространства состояний $$u^{∗}$$, что $$f(u^{∗}) = 0$$. | |
| − | + | ||
| − | + | ===Устойчивость неподвижных точек=== | |
| − | |||
| − | |||
| − | + | Определения для устойчивости по Ляпунову и асимптотической устойчивости полностью повторяют определения из раздела, посвященному динамическим системам с дискретным временем. | |
| − | + | '''Теорема 2.''' | |
| − | + | Пусть $$u^*$$ — положение равновесия системы (\ref{sistnepr}). Функция $$f(u)$$ и ее производная $$f'(u)$$ определены и непрерывны для любых $$u \in \mathcal{U}$$. Тогда | |
| − | + | ||
| − | + | 1) если $$f'(u^*)<0$$, то $$u^*$$ — асимптотически устойчиво. | |
| − | + | 2) если $$f'(u^*)>0$$, то $$u^*$$ — неустойчиво. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | '''Доказательство:''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Пусть $$u^*$$ — положение равновесия системы (\ref{sistnepr}). | |
| + | Зададим небольшое отклонение $$\xi$$ переменной $$u$$ от ее стационарного значения $$u^*$$ : $$u=u^*+\xi$$, такое, что $$\frac{\xi}{u^*} \ll 1$$. Таким образом получим: | ||
| − | \begin{equation | + | \begin{equation} |
| − | \ | + | \frac{d(u^* + \xi)}{dt} = f(u^* + \xi) |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\end{equation} | \end{equation} | ||
| − | + | Так как $$\frac{d u^*}{d t}=0$$, перейдем от переменной $$u$$ к переменной $$\xi$$: | |
| − | + | \begin{equation} \label{ur1} | |
| − | + | \frac{d\xi}{dt} = f(u^* + \xi) | |
| − | + | \end{equation} | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Уравнение (\ref{ur1}) определяет поведение во времени отклонения $$\xi=u-u^*$$ от стационарного состояния. Решение уравнения (\ref{ur1}) $$\xi(t)$$ вблизи нулевой точки $$\xi = 0$$ будет совпадать с решением $$u(t)$$ динамической системы (\ref{sistnepr}) вблизи стационарного состояния $$u^*$$. | |
| + | Правая часть уравнения (\ref{ur1}) указывает величину скорости, с которой отклонение $$\xi(t)$$ будет увеличиваться или уменьшаться с течением времени. | ||
| − | + | В терминах новой переменной $$\xi(t)$$ стационарное состояние | |
| + | будет ''устойчивым по Ляпунову'', если, задав любое сколь угодно | ||
| + | малое $$\varepsilon>0$$, всегда можно найти такое $$\delta>0$$, что | ||
| + | $$\xi(t)<\varepsilon$$ для $$t_0 \leqslant t$$, если $$|\xi(t_0)|<\delta$$, | ||
| + | и ''асимптотически устойчивым'', если отклонение $$\xi(t)$$ стремится | ||
| + | к нулю, т.е. $$\displaystyle{\lim_{t\to\infty}}|\xi(t)|=0$$. | ||
| − | + | Разложим функцию $$f(u^*+\xi)$$ в | |
| − | + | [https://ru.wikipedia.org/wiki/%D0%A0%D1%8F%D0%B4_%D0%A2%D0%B5%D0%B9%D0%BB%D0%BE%D1%80%D0%B0 ряд Тейлора] | |
| + | в точке $$\xi_0=0$$: | ||
\[ | \[ | ||
| − | + | \frac{d \xi}{dt}=f(u^*)+f'(u^*)\xi+\frac{1}{2}f''(u^*)\xi^2+... | |
| − | |||
| − | |||
| − | |||
\] | \] | ||
| − | + | Учитывая, что $$f(u^*)=0$$, получим | |
| − | |||
\[ | \[ | ||
| − | + | \frac{d \xi}{dt}=a_1 \xi+a_2\xi^2+..., | |
| − | |||
| − | |||
| − | |||
\] | \] | ||
| + | где $$a_1=f'_u(u^*), a_2=\frac{1}{2}f'_{uu}(u^*),...$$ . | ||
| − | + | Поскольку вблизи точки $$\xi_0=0$$ всегда можно выделить достаточно малую окрестность, где вклад нелинейных членов разложения | |
| − | + | становится пренебрежимо малым по сравнению с вкладом линейных членов, можно отбросить члены порядка 2 и | |
| − | + | выше. Получим линеаризованное уравнение, или уравнение первого приближения, которое, опуская нижний индекс, можно записать как: | |
| − | |||
\[ | \[ | ||
| − | + | \frac{d \xi}{dt}=a \xi, | |
| − | |||
| − | |||
| − | |||
\] | \] | ||
| + | где $$a=f'_u(u^*)$$. | ||
| − | + | Решим полученное линейное уравнение. Разделяя переменные, | |
| + | проинтегрируем обе части уравнения: | ||
\[ | \[ | ||
| − | \ | + | \int \frac{d \xi}{d \xi}=a \int dt, |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
\] | \] | ||
\[ | \[ | ||
| − | + | \ln|\xi|=at + C, | |
\] | \] | ||
| − | + | Переходя от логарифмов к значениям переменной $$\xi$$ и определяя произвольную постоянную $$С$$ из начальных условий, получим: | |
| − | + | ||
\[ | \[ | ||
| − | + | \xi(t) = \xi(t_0) e^{at}, | |
\] | \] | ||
| + | где $$\xi(t_0)$$ — значение переменной $$\xi(t)$$ в начальный момент времени. | ||
| + | |||
| − | + | Если $$a<0$$, то $$\xi \to \infty$$ при $$t \to \infty$$, следовательно, отклонение от | |
| − | + | стационарного состояния $$u^*$$ со временем затухает, тогда стационарное состояние $$u^*$$ по определению устойчиво. | |
| − | |||
| − | |||
| − | |||
| − | + | Если $$a>0$$, то $$\xi \to \infty$$ при $$t \to \infty$$, то есть отклонение от стационарного состояния $$u^*$$ будет со временем возрастать, тогда стационарное состояние $$u^*$$ неустойчиво. | |
| − | + | Если $$a=0$$, то анализ уравнения первого приближения не может дать ответа на вопрос об устойчивости стационарного состояния системы. | |
| + | $$\blacksquare$$ | ||
| − | + | == Связанные теоремы == | |
| − | + | '''Теорема 3. (Банах)''' | |
| − | + | Пусть $$(X, d)$$ — полное [https://sawiki.cs.msu.ru/index.php/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE метрическое пространство] с метрикой $$d$$. | |
| − | + | Пусть задано отображение $$f : X \rightarrow X$$ и существует число | |
| + | $$a, 0 \leqslant a < 1$$, такое, что для любых $$x, y \in X: d(f(x), f(y)) \leqslant a \cdot d(x, y)$$. | ||
| − | + | Тогда существует единственная точка $$\xi \in X$$ такая, что $$f(\xi) = \xi$$, и начиная | |
| + | с любой точки $$x_0 \in X$$, последовательность итераций $${f_n(x_0)}_{n=1,2,...}$$ сходится к | ||
| + | точке $$\xi$$. | ||
| − | + | '''Теорема 4. (Брауэр)''' | |
| − | + | Любое непрерывное отображение замкнутого шара в себя в конечномерном | |
| − | + | [https://ru.wikipedia.org/wiki/%D0%95%D0%B2%D0%BA%D0%BB%D0%B8%D0%B4%D0%BE%D0%B2%D0%BE_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE евклидовом] | |
| + | пространстве имеет неподвижную точку. | ||
| − | + | Более подробно, рассмотрим замкнутый шар в $$n$$-мерном пространстве <math>B^n\subset \mathbb R^n</math>. Пусть <math>f \colon B^n\to B^n</math> — некоторое непрерывное отображение этого шара в себя (не обязательно строго внутрь себя, не обязательно биективное, т.е. даже не обязательно сюръективное). Тогда найдется такая точка <math>x\in B^n</math>, что <math>f(x)=x</math>. | |
| − | '''Теорема | + | '''Теорема 5. (Шаудер — Тихонов)''' |
| − | + | В локально выпуклом топологическом векторном пространстве любое непрерывное отображение $$f : K\to K$$ выпуклого | |
| − | + | [https://sawiki.cs.msu.ru/index.php/%D0%9A%D0%BE%D0%BC%D0%BF%D0%B0%D0%BA%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%B8_%D0%BF%D1%80%D0%B5%D0%B4%D0%BA%D0%BE%D0%BC%D0%BF%D0%B0%D0%BA%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C компактного множества] | |
| − | + | $$K$$ в себя имеет неподвижную точку. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Список литературы== | ==Список литературы== | ||
| − | 1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011. | + | 1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии, 2011. |
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023. | 2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023. | ||
3. Banach S. Sur les opérations dans les ensembles abstraits et leur applications aux | 3. Banach S. Sur les opérations dans les ensembles abstraits et leur applications aux | ||
| − | équations integrales, Fund. Math. | + | équations integrales, Fund. Math, 1922 |
| + | |||
| + | 4. Шашкин Ю.А. Неподвижные точки, М.: Наука, 1989 | ||
| + | |||
| + | 5. J. Schauder, Der Fixpunktsatz in Funktionalräumen, Studia Math. 2, 1930 | ||
Текущая версия на 22:54, 20 декабря 2023
Содержание
Случай динамических систем с дискретным временем
Пусть задана динамическая система:
\begin{equation} \label{sist1} u_{t+1} = f(u_t), u_{t=0}=u_0,\ u_t \in \mathbb{R}^n,\ f : \mathbb{R}^n → \mathbb{R}^n. \end{equation}
Определение 1.
Неподвижными точками динамической системы (\ref{sist1}) называются такие точки пространства состояний $$u^{∗}$$, что $$f(u^{∗}) = u^{∗}$$.
Кроме термина неподвижная точка используют иногда термины стационарная точка или положение равновесия.
Устойчивость неподвижных точек
Реальная система подвержена внешним воздействиям, она не может находиться все время в одном и том же состоянии. Если немного возмутить состояние системы так, что ее состояние окажется в некоторой окрестности положения равновесия, то возможны следующие сценарии: траектории могут покинуть эту окрестность, остаться в этой окрестности, или приблизиться к положению равновесия. Естественно назвать положение равновесия неустойчивым в первом случае и устойчивым в двух других.
Определение 2.
Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется устойчивой по Ляпунову, если для любого $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что для любых начальных данных $$u(t_0)$$ из $$\delta$$-окрестности точки $$u^{*}$$ вся траектория системы $$u(t)$$ содержится в $$\varepsilon$$-окрестности точки $$u^{*}$$.
$$\forall \varepsilon > 0 ~ \exists \delta(\varepsilon)>0 ~ \forall u(t_0) \in \mathcal{U}_{\delta}(u^{*})$$, $$|u^{*}-u(t)|< \varepsilon, ~\forall t \geqslant t_0$$.
Определение 3.
Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется асимптотически устойчивой, если она является устойчивой по Ляпунову и $$\displaystyle{\lim_{t\to\infty}} u(t) = u^{*}$$.
Если положение равновесия не является устойчивым, то говорят, что оно неустойчиво.
Асимптотически устойчивые неподвижные точки иногда называют аттракторами, а неустойчивые неподвижные точки иногда называют репеллерами.
Теорема 1.
Пусть $$u^{*}$$ — неподвижная точка отображения (\ref{sist1}), т.е. $$u^{*}$$ = $$f(u^{*})$$, и пусть $$f$$ обратима в малой окрестности $$u^{*}$$. Тогда $$u^{*}$$ асимптотически устойчива, если $$|f^{'}(u^{*})| < 1$$, и неустойчива, если $$|f^{'}(u^{*})| > 1$$. Если $$ |f^{'}(u^{*})| = 1$$, то требуются дополнительные исследования.
Доказательство:
Пусть $$|f^{'}(u^{*})| < 1$$ и пусть $$u$$ принадлежит малой окрестности $$u^{*}$$. Так как \[ \displaystyle{\lim_{t\to\infty}} \frac{|f(u)-f(u^{*})|}{|u-u^{*}|}=|f^{'}(u^{*})|, \] поэтому существует такая окрестность $$u^{*}$$, что \[ \frac{|f(u)-f(u^{*})|}{|u-u^{*}|} \leqslant a, \] для всех $$u$$ из этой окрестности; здесь $$a$$ — некоторое число, такое что $$|f^{'}(u^{*})| \leqslant a < 1$$. Таким образом, $$f(u)$$ остается в той же окрестности, что и $$u$$, и, кроме того, ближе к неподвижной точке $$u^{*}$$, по крайней мере, на множитель $$a$$. Отсюда следует, что \[|f(f(u)) − f(f(u^{*}))| \leqslant a |f(u) − f(u^{*})| \leqslant a^2|u − u^{*}|, \] или, по индукции, \[|f^{k}(u) − u^{*}| \leqslant a^{k}|u − u^{*}|, \] где $$f^{k}$$ обозначает $$k$$-ую суперпозицию отображения $$f$$. Таким образом мы доказали, что последовательность $$f^{k}(u)$$ будет сходиться к $$u^{*}$$, то есть является асимптотически устойчивой.
Вторая часть утверждения доказывается сходным образом. $$\blacksquare$$
Пример поиска неподвижных точек с помощью графического метода
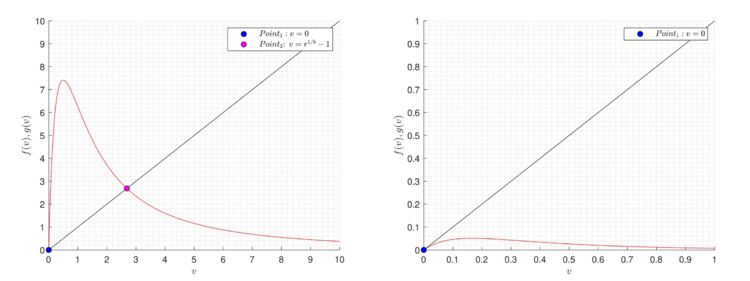
Пусть задана система $$v_{t+1} = \frac{r v_t}{(1+ v_t)^b}$$.
Графически неподвижные точки — это точки пересечения графика функции $$f(v)$$ и биссектрисы первого координатного угла $$v_{t+1} = v_{t}$$ (нас интересуют только неотрицательные решения). Для нахождения неподвижных точек заданной системы рассмотрим возможные пересечения графика функции $$f(v)=\frac{rv}{(1+v)^b}$$ с прямой $$g(v)=v$$.
Заметим, что система \begin{equation} \label{sist2} \begin{cases} f(v)=\frac{rv}{(1+v)^b},\\g(v)=v. \end{cases} \end{equation} при любых $$v \geqslant 0, ~r,b > 0$$ имеет хотя бы один корень, а именно $$v=0$$. Второй корень $$v=r^{1/b}-1$$ система может иметь только при значении параметра $$r>1$$. Больше двух неотрицательных корней система (\ref{sist2}) не имеет.
Пример исследования неподвижных точек на устойчивость
Исследуем на устойчивость неподвижные точки $$v^{*}=r^{1/b}-1$$ и $$v^{*}=0$$ для системы (\ref{sist2}).
\[ f_v(v^{*})=\frac{r((1+v)^b-bv(1+v)^{b-1})}{(1+v)^{2b}}. \]
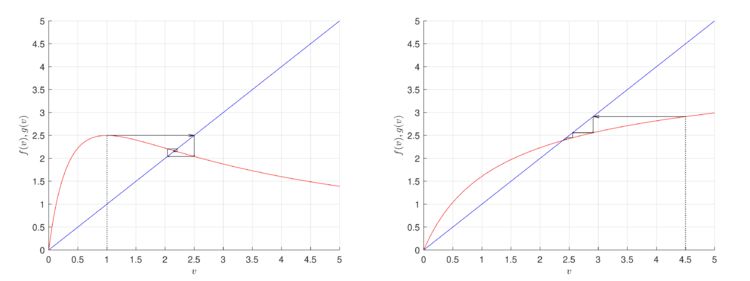
1. Исследование первой точки $$v^{*}=r^{1/b}-1$$:
Подставим $$v^{*}=r^{1/b}-1$$ в выражение (\ref{sist2}) и с учетом наложенных ограничений $$r>1, b>0$$ для существования точки получим
\[ f_v(v^{*})=b(r^{-1/b}-1)+1. \]
Согласно теореме 1 точка $$v^{*}=r^{1/b}-1$$ будет:
Асимптотически устойчивой, при $$r^{-1/b}<1$$.
Неустойчивой, при $$r^{-1/b}>1$$.
Отметим, что точка $$v^{*}=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, точка $$v^{*}=r^{1/b}-1$$ асимптотически устойчива всегда, если она существует.
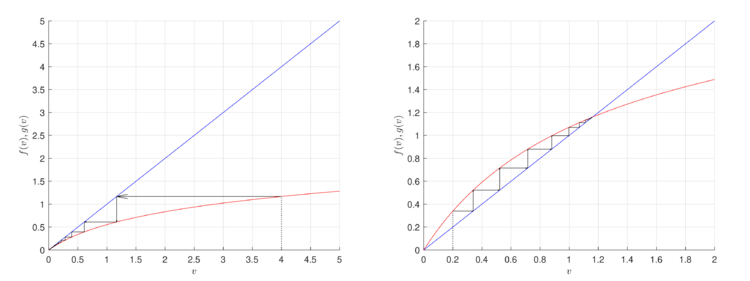
2. Исследование второй точки $$v^{*}=0$$:
Подставим $$v^{*}=0$$ в выражение (\ref{sist2}) и получим \[ f_v(v^{*})=r. \] Таким образом, по теореме 1, точка $$v^{*}=0$$ будет:
Асимптотически устойчивой, при $$r<1$$.
Неустойчивой, при $$r>1$$.
Случай динамических систем с непрерывным временем
Пусть задана динамическая система:
\begin{equation} \label{sistnepr} \dot{u} = f(u),\ u \in U \subseteq \mathbb{R}^n,\ f : U → \mathbb{R}^n. \end{equation}
Определение 4.
Неподвижными точками динамической системы (\ref{sistnepr}) называются такие точки пространства состояний $$u^{∗}$$, что $$f(u^{∗}) = 0$$.
Устойчивость неподвижных точек
Определения для устойчивости по Ляпунову и асимптотической устойчивости полностью повторяют определения из раздела, посвященному динамическим системам с дискретным временем.
Теорема 2.
Пусть $$u^*$$ — положение равновесия системы (\ref{sistnepr}). Функция $$f(u)$$ и ее производная $$f'(u)$$ определены и непрерывны для любых $$u \in \mathcal{U}$$. Тогда
1) если $$f'(u^*)<0$$, то $$u^*$$ — асимптотически устойчиво.
2) если $$f'(u^*)>0$$, то $$u^*$$ — неустойчиво.
Доказательство:
Пусть $$u^*$$ — положение равновесия системы (\ref{sistnepr}). Зададим небольшое отклонение $$\xi$$ переменной $$u$$ от ее стационарного значения $$u^*$$ : $$u=u^*+\xi$$, такое, что $$\frac{\xi}{u^*} \ll 1$$. Таким образом получим:
\begin{equation} \frac{d(u^* + \xi)}{dt} = f(u^* + \xi) \end{equation}
Так как $$\frac{d u^*}{d t}=0$$, перейдем от переменной $$u$$ к переменной $$\xi$$:
\begin{equation} \label{ur1} \frac{d\xi}{dt} = f(u^* + \xi) \end{equation}
Уравнение (\ref{ur1}) определяет поведение во времени отклонения $$\xi=u-u^*$$ от стационарного состояния. Решение уравнения (\ref{ur1}) $$\xi(t)$$ вблизи нулевой точки $$\xi = 0$$ будет совпадать с решением $$u(t)$$ динамической системы (\ref{sistnepr}) вблизи стационарного состояния $$u^*$$. Правая часть уравнения (\ref{ur1}) указывает величину скорости, с которой отклонение $$\xi(t)$$ будет увеличиваться или уменьшаться с течением времени.
В терминах новой переменной $$\xi(t)$$ стационарное состояние будет устойчивым по Ляпунову, если, задав любое сколь угодно малое $$\varepsilon>0$$, всегда можно найти такое $$\delta>0$$, что $$\xi(t)<\varepsilon$$ для $$t_0 \leqslant t$$, если $$|\xi(t_0)|<\delta$$, и асимптотически устойчивым, если отклонение $$\xi(t)$$ стремится к нулю, т.е. $$\displaystyle{\lim_{t\to\infty}}|\xi(t)|=0$$.
Разложим функцию $$f(u^*+\xi)$$ в ряд Тейлора в точке $$\xi_0=0$$:
\[ \frac{d \xi}{dt}=f(u^*)+f'(u^*)\xi+\frac{1}{2}f''(u^*)\xi^2+... \]
Учитывая, что $$f(u^*)=0$$, получим \[ \frac{d \xi}{dt}=a_1 \xi+a_2\xi^2+..., \] где $$a_1=f'_u(u^*), a_2=\frac{1}{2}f'_{uu}(u^*),...$$ .
Поскольку вблизи точки $$\xi_0=0$$ всегда можно выделить достаточно малую окрестность, где вклад нелинейных членов разложения становится пренебрежимо малым по сравнению с вкладом линейных членов, можно отбросить члены порядка 2 и выше. Получим линеаризованное уравнение, или уравнение первого приближения, которое, опуская нижний индекс, можно записать как: \[ \frac{d \xi}{dt}=a \xi, \] где $$a=f'_u(u^*)$$.
Решим полученное линейное уравнение. Разделяя переменные, проинтегрируем обе части уравнения:
\[ \int \frac{d \xi}{d \xi}=a \int dt, \]
\[ \ln|\xi|=at + C, \]
Переходя от логарифмов к значениям переменной $$\xi$$ и определяя произвольную постоянную $$С$$ из начальных условий, получим:
\[ \xi(t) = \xi(t_0) e^{at}, \] где $$\xi(t_0)$$ — значение переменной $$\xi(t)$$ в начальный момент времени.
Если $$a<0$$, то $$\xi \to \infty$$ при $$t \to \infty$$, следовательно, отклонение от
стационарного состояния $$u^*$$ со временем затухает, тогда стационарное состояние $$u^*$$ по определению устойчиво.
Если $$a>0$$, то $$\xi \to \infty$$ при $$t \to \infty$$, то есть отклонение от стационарного состояния $$u^*$$ будет со временем возрастать, тогда стационарное состояние $$u^*$$ неустойчиво.
Если $$a=0$$, то анализ уравнения первого приближения не может дать ответа на вопрос об устойчивости стационарного состояния системы. $$\blacksquare$$
Связанные теоремы
Теорема 3. (Банах)
Пусть $$(X, d)$$ — полное метрическое пространство с метрикой $$d$$.
Пусть задано отображение $$f : X \rightarrow X$$ и существует число $$a, 0 \leqslant a < 1$$, такое, что для любых $$x, y \in X: d(f(x), f(y)) \leqslant a \cdot d(x, y)$$.
Тогда существует единственная точка $$\xi \in X$$ такая, что $$f(\xi) = \xi$$, и начиная с любой точки $$x_0 \in X$$, последовательность итераций $${f_n(x_0)}_{n=1,2,...}$$ сходится к точке $$\xi$$.
Теорема 4. (Брауэр)
Любое непрерывное отображение замкнутого шара в себя в конечномерном евклидовом пространстве имеет неподвижную точку.
Более подробно, рассмотрим замкнутый шар в $$n$$-мерном пространстве \(B^n\subset \mathbb R^n\). Пусть \(f \colon B^n\to B^n\) — некоторое непрерывное отображение этого шара в себя (не обязательно строго внутрь себя, не обязательно биективное, т.е. даже не обязательно сюръективное). Тогда найдется такая точка \(x\in B^n\), что \(f(x)=x\).
Теорема 5. (Шаудер — Тихонов)
В локально выпуклом топологическом векторном пространстве любое непрерывное отображение $$f : K\to K$$ выпуклого компактного множества $$K$$ в себя имеет неподвижную точку.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии, 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.
3. Banach S. Sur les opérations dans les ensembles abstraits et leur applications aux équations integrales, Fund. Math, 1922
4. Шашкин Ю.А. Неподвижные точки, М.: Наука, 1989
5. J. Schauder, Der Fixpunktsatz in Funktionalräumen, Studia Math. 2, 1930