Фазовые и интегральные кривые. Фазовое пространство: различия между версиями
Akbar23 (обсуждение | вклад) |
Akbar23 (обсуждение | вклад) |
||
| Строка 93: | Строка 93: | ||
| − | ==Список литературы== | + | == Список литературы == |
| − | + | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | |
| − | + | # Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011. | |
| − | |||
| − | |||
Текущая версия на 11:16, 29 декабря 2023
Множество всевозможных состояний динамической системы называется фазовым пространством этой системы.
Пусть дана динамическая система: \begin{equation} \label{eq:0} \frac{du}{dt} = f(u),\ u \in U \subseteq \mathbb{R}^n,\ f:U \rightarrow \mathbb{R}^n,\ f \in C^1(U). \end{equation} Множество $$U$$ возможных состояний $$u$$ — фазовое пространство системы \eqref{eq:0}.
Обозначим за $$u = u(t, u_0)$$ решение системы \eqref{eq:0} с начальным условием $$u(0) = u_0$$. Множество точек $$\{ t, u(t, u_0) \}$$ называется интегральной кривой системы \eqref{eq:0}, а множество точек $$\{ u(t, u_0)\}$$ называется фазовой кривой системы \eqref{eq:0}.
Интегральные кривые дают полную информацию о поведении решений системы \eqref{eq:0}, а вот фазовые кривые эту информацию не дают, так как являются лишь проекциями интегральных кривых на фазовое пространство. Но в большинстве случаев достаточно изучить фазовые кривые.
Свойства фазовых кривых
Свойство 1. Пусть $$u = u(t)$$ — решение задачи \eqref{eq:0}. Тогда $$u = u(t + c)$$, где $$c$$ — любая постоянная, — также решение задачи \eqref{eq:0}.
Доказательство. Доказательство следует из следующей цепочки равенств: \begin{equation} \frac{du(t + c)}{dt} = \frac{du(t + c)}{d(t + c)} = f(u(t + c)). \end{equation} Свойство 2. Две фазовые кривые либо не имеют общих точек, либо совпадают. Это свойство означает, что фазовое пространство расслаивается на непересекающиеся фазовые кривые.
Доказательство. Пусть $$\phi , \psi$$ — интегральные кривые, и соответствующие им фазовые кривые пересекаются в точке $$u_0$$. Это означает, что существуют такие решения $$u_1 = \phi(t, u_0)$$ и $$u_2 = \psi(t, u_0)$$ и такие $$t_1$$ и $$t_2$$, что $$\phi (t_1,u_0) = \psi (t_2,u_0).$$ Пусть $$\chi (t, u_0) = \psi (t + (t_1 − t_2), u_0).$$ Из первого свойства следует, что $$u = \chi (t, u_0)$$ есть решение системы \eqref{eq:0}. С другой стороны, $$\chi (t_2, u_0) = \phi(t_1, u_0) = \psi(t_2, u_0)$$. Следовательно, две интегральные кривые $$\chi$$ и $$\psi$$ проходят через одну и ту же точку $$u_0$$ в момент времени $$t_2$$. Из теоремы существования и единственности решения задачи Коши для системы \eqref{eq:0}, следует, что эти кривые совпадают. Но фазовая траектория, соответствующая интегральной кривой $$\chi$$, та же самая, что и соответствующая интегральной кривой $$\phi$$. Следовательно, фазовые траектории $$\phi$$ и $$\psi$$ совпадают.
Свойство 3. Если точка $$u^*$$ — неподвижная точка системы \eqref{eq:0}, то точка $$u = u^*$$ есть фазовая кривая.
Доказательство. $$u^*$$ — неподвижная точка системы \eqref{eq:0}, значит, что $$f(u^*) = 0$$. Тогда система \eqref{eq:0} преобразуется в вид $$\frac{du}{dt} = 0$$. Решением этого дифференциального уравнения является $$u(t) =$$ const, возьмем const $$= u^*$$. Получается, что $$u = u^*$$ является решением системы \eqref{eq:0}, а значит и фазовой кривой.
Свойство 4. Фазовая кривая, отличная от точки, есть гладкая кривая, то есть в каждой точке имеется ненулевой касательный вектор, непрерывно зависящий от длины дуги.
Доказательство. Предположим, что фазовая траектория удовлетворяет системе \eqref{eq:0} с начальным условием $$u(0) = u_0$$. Теорема о существовании и единственности решений задачи Коши утверждает, что если $$f(u)$$ является непрерывной функцией, то существует единственное решение этого уравнения, проходящее через точку $$u_0$$. Более того, это решение будет гладким, дифференцируемым и иметь непрерывно зависящий касательный вектор в каждой точке. Таким образом, фазовая траектория, отличная от точки, будет представлена гладкой кривой, так как она будет являться решением дифференциального уравнения и удовлетворять условиям теоремы о существовании и единственности решений обыкновенных дифференциальных уравнений.
Свойство 5. Всякая фазовая кривая принадлежит одному из трех типов: гладкая кривая без самопересечений; замкнутая гладкая кривая (цикл); точка.
Цикл — периодическая траектория, не являющаяся положением равновесия, каждая точка которой удовлетворяет условию $$u(t + T_0, u_0) = u(t, u_0)$$ для некоторого $$T_0 > 0$$ и всех $$t \in \mathbb{R}$$.
Доказательство. Если фазовая траектория не есть точка, то она, в силу предыдущего пункта, является гладкой кривой, гладкая кривая либо замкнута, либо незамкнута.
Примеры
Для рассмотрения примеров нам понадобится определение фазового потока.
Пусть фазовое пространство $$U$$ представляет собой многомерное пространство или область в нем, а время непрерывно. Допустим, что нам известно, с какой скоростью движется каждая точка $$u$$ фазового пространства. Иными словами, известна вектор-функция скорости $$f(u)$$. Тогда траектория точки $$u_0\in U$$ будет решением автономного дифференциального уравнения $$\frac{du}{dt}=f(u)$$ с начальным условием $$u(0) = u_0$$. Заданная таким образом динамическая система называется фазовым потоком для автономного дифференциального уравнения.
Пример 1.
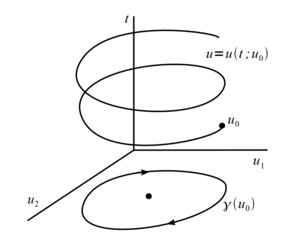
Рассмотрим следующую динамическую систему \begin{equation} \label{eq:1} \begin{cases} \dot{u}_1 = u_2 ,\\ \dot{u}_2 = -u_1. \end{cases} \end{equation} Общее решение имеет вид $$u_1(t) = C\ \sin(t + \alpha_0), u_2(t) = C\ \cos(t + \alpha_0)$$, где $$C$$ и $$\alpha_0$$ — постоянные, определяемые начальными условиями. Интегральная кривая представляет собой винтовую линию, намотанную на цилиндр $$u_1^2+u_2^2 = C^2$$ в пространстве $$(u_1, u_2, t)$$. Фазовые кривые системы \eqref{eq:1} являются окружностями $$u_1^2+u_2^2 = C^2$$ в фазовом пространстве $$(u_1, u_2)$$.
Пример 2.
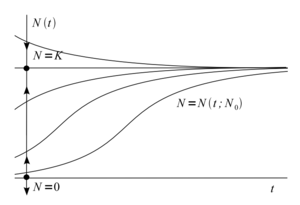
Рассмотрим одномерную динамическую систему, задаваемую логистическим уравнением \begin{equation} \label{eq:2} \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right). \end{equation} Решение системы при начальном условии $$N=N_0$$ представляется следующим образом: \begin{equation} \label{eq:3} N(t) = \dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . \end{equation} Фазовое пространство в этом случае одномерно. Стрелками отмечено направление движения фазового потока на оси $$N$$. Фазовые траектории системы представляют собой отрезки прямой $$N$$, движение по которым происходит в направлении точки с координатой $$K$$.
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.