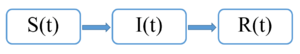Математическая модель распространения эпидемий: различия между версиями
Taisia23 (обсуждение | вклад) |
Taisia23 (обсуждение | вклад) м |
||
| (не показано 11 промежуточных версий этого же участника) | |||
| Строка 9: | Строка 9: | ||
<br> | <br> | ||
<br> | <br> | ||
| − | [[Файл:SIR-model.png|мини|Диаграмма эволюции особи популяции в SIR-модели]] | + | [[Файл:SIR-model.png|мини|Рис. 1. Диаграмма эволюции особи популяции в SIR-модели]] |
В SIR-модели все особи поделены на 3 группы: | В SIR-модели все особи поделены на 3 группы: | ||
# <math>S(t)</math> — подверженные заболеванию особи (от англ. ''susceptible'') | # <math>S(t)</math> — подверженные заболеванию особи (от англ. ''susceptible'') | ||
| Строка 37: | Строка 37: | ||
</math> | </math> | ||
| − | Здесь <math>p</math> — вероятность заражения, а <math>c</math> — среднее число контактов в единицу времени. Промежуток времени <math>t \in [T_1,\ T_2]</math> — окно, в течение которого | + | Здесь <math>p</math> — вероятность заражения, а <math>c</math> — среднее число контактов в единицу времени. Промежуток времени <math>t \in [T_1,\ T_2]</math> — окно, в течение которого индивид заразен. |
<br> | <br> | ||
<br> | <br> | ||
Таким образом, в частном случае <math>A(\tau)</math> можно ввести так:: | Таким образом, в частном случае <math>A(\tau)</math> можно ввести так:: | ||
| − | <math> A(\tau) = \underbrace{\beta N}_{c} \cdot \underbrace{\exp\{ -\gamma\tau \} }_{p},\ \ \beta=const,</math> | + | <math> A(\tau) = \underbrace{\beta N}_{c} \cdot \underbrace{\exp\{ -\gamma\tau \} }_{p},\ \ \beta=const>0,</math> |
| − | то есть | + | то есть промежуток времени для заражения других особей [https://ru.wikipedia.org/wiki/%D0%AD%D0%BA%D1%81%D0%BF%D0%BE%D0%BD%D0%B5%D0%BD%D1%86%D0%B8%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B5_%D1%80%D0%B0%D1%81%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5 распределен экспоненциально] со средним <math>\frac{1}{\gamma}</math>. Следовательно, средняя длина промежутка времени, в течение которого индивид заразен, равна <math>\frac{1}{\gamma}</math>. |
<br> | <br> | ||
<br> | <br> | ||
| − | '''''Замечание.''''' Введя подобным образом функцию инфективности, получают, что число контактов растёт линейно с общим объёмом популяции <math>N</math>, что, вообще говоря, является довольно грубым допущением. Однако оно необходимо для упрощения и наглядности | + | '''''Замечание.''''' Введя подобным образом функцию инфективности, получают, что число контактов растёт линейно с общим объёмом популяции <math>N</math>, что, вообще говоря, является довольно грубым допущением. Однако оно необходимо для упрощения исследования и его наглядности. |
===Получение аналитического вида SIR-модели=== | ===Получение аналитического вида SIR-модели=== | ||
| Строка 53: | Строка 53: | ||
<math>i(t) = \frac{S(t)}{N} \int\limits_0^{\infty} A(\tau) i(t-\tau) d\tau.</math> | <math>i(t) = \frac{S(t)}{N} \int\limits_0^{\infty} A(\tau) i(t-\tau) d\tau.</math> | ||
| − | + | Интеграл в правой части можно трактовать как среднее число "удачных" контактов (т.е. таких, при которых заражение произошло). Причём, в силу выведенной связи на <math>i(t)</math> и <math>S(t)</math> можно получить следующее:: | |
| + | <math> | ||
| + | \begin{equation} | ||
| + | \dot{S}(t) = \frac{S(t)}{N} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau. \label{sys2} | ||
| + | \end{equation} | ||
| + | </math> | ||
| + | <br> | ||
| + | <br> | ||
| + | Далее вводится <math>I(t)</math> следующим образом:: | ||
| + | <math> I(t) = -\frac{1}{\beta} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau\ =\ \{s:=t-\tau\}\ =\ | ||
| + | -\frac{1}{\beta} \int\limits_{-\infty}^t A(t-s) \dot{S}(s) ds\ =\ \{ \tau:=s\}\ =\ -\frac{1}{\beta} \int\limits_{-\infty}^t A(t-\tau) \dot{S}(\tau) d\tau.</math> | ||
| + | С учётом того, что функция инфективности <math> A(\tau) </math> введена так, что <math> \dot{A}(\tau) = -\gamma A(\tau)</math>, [https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%9B%D0%B5%D0%B9%D0%B1%D0%BD%D0%B8%D1%86%D0%B0_(%D0%BF%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D0%BD%D0%BE%D0%B9_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D0%B0_%D1%81_%D0%BF%D0%B0%D1%80%D0%B0%D0%BC%D0%B5%D1%82%D1%80%D0%BE%D0%BC) продифференцируем полученное равенство по параметру] <math>t</math>:: | ||
| + | <math> | ||
| + | \dot{I}(t) = -\frac{1}{\beta} A(0) \dot{S}(t) + \frac{1}{\beta} \underbrace{A(\infty)}_{= 0}\dot{S}(-\infty) - \frac{1}{\beta} \int\limits_{-\infty}^t \left( -\gamma A(t-\tau) \dot{S}(\tau) \right) d\tau = | ||
| + | </math> | ||
| + | : | ||
| + | <math> | ||
| + | = -\frac{\beta N}{\beta}\dot{S}(t) + \gamma\cdot \underbrace{ \frac{1}{\beta} \int\limits_{-\infty}^t A(t-\tau) \dot{S}(\tau) d\tau}_{= - I(t)} = \{ \text{в силу } (\ref{sys2}) \} = \underbrace{-\frac{N S(t)}{N} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau}_{=\beta SI} - \gamma I(t) = \beta S(t)I(t) - \gamma I(t). | ||
| + | </math> | ||
| + | |||
| + | Таким образом, для <math>I(t)</math> получается следующее уравнение динамики — <math> \dot{I}(t) = \beta S(t) I(t) - \gamma I(t) = I(t) \left( \beta S(t) - \gamma \right)</math>. | ||
| + | <br> | ||
| + | <br> | ||
| + | Итоговая динамическая система, описывающая SIR-модель, выглядит следующим образом:: | ||
| + | <math> | ||
| + | \begin{equation} | ||
| + | \begin{cases} | ||
| + | \dot{S}(t) = - \beta S(t) I(t),\\ | ||
| + | \dot{I}(t) = I(t)\left( \beta S(t) - \gamma \right),\\ | ||
| + | \dot{S}(t) + \dot{I}(t) + \dot{R}(t) = 0. | ||
| + | \end{cases} \label{sys3} | ||
| + | \end{equation} | ||
| + | </math> | ||
| + | Последнее уравнение системы следует из её замкнутости, упомянутой выше. Причём из системы <math>(\ref{sys3})</math> можно выразить и динамику класса переболевших — <math> \dot{R}(t) = \gamma I(t)</math>. | ||
| + | |||
| + | ===Анализ SIR-модели=== | ||
| + | Исследуя полученную динамическую систему <math>(\ref{sys3})</math> SIR-модели, можно заметить, что по переменной <math>I</math> существует [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B особая точка] при <math>S = \frac{\gamma}{\beta} := \sigma</math>. При <math> S(t) > \sigma</math> число инфицированных растёт, и, наоборот, при <math> S(t) < \sigma</math> — убывает. | ||
| + | <br> | ||
| + | <br> | ||
| + | Однако из первого уравнения системы <math>(\ref{sys3})\ \ \dot{S}(t)\leqslant 0</math>, поэтому поведение системы разделяется на два существенно разных случая в зависимости от начального количества подверженных заболеванию <math> S_0 </math>: | ||
| + | # <math> S_0 < \sigma\ \Longrightarrow</math> эпидемии в системе нет, поскольку число заражённых монотонно уменьшается до нуля; | ||
| + | # <math> S_0 > \sigma\ \Longrightarrow</math> происходит эпидемия в системе. | ||
| + | <br> | ||
| + | [[Файл:SIR-s0.png|700px|центр|мини|Рис. 2. Временная эволюция численностей здоровых, заболевших и переболевших особей для SIR-модели. <br> (а) В системе есть эпидемия с максимальным числом заболевших <math>I_{max}</math>. Параметры <math>\sigma = 500,\ \gamma = 5,</math> <math>N=1000,\ S_0=994,\ I_0=2.</math> | ||
| + | <br> (б) В системе не возникает эпидемия, так как <math>S_0<\sigma</math>. Параметры <math>\sigma = 800,\ \gamma = 5,\ N=1000,\ S_0=700.</math>]] | ||
| + | |||
| + | Рассмотрим далее случай, когда в системе возникает эпидемия. Важным прикладным результатом исследования такой системы является, например, '''максимальное количество инфицированных''', поскольку это помогает рассчитать эффективное число койко-мест в больницах во время пика эпидемии. На рис. 2 (а) можно наблюдать этот пик, обозначенный за <math>I_{max}</math>. Можно найти его значение аналитически, исследовав <math>\frac{dI}{dS}</math>:: | ||
| + | |||
| + | <math> | ||
| + | \frac{dI}{dS} = \frac{\beta SI - \gamma I}{-\beta SI} = -1 + \frac{\sigma}{S}\ \ \Longrightarrow\ \ I+S-\sigma\ln S = const. | ||
| + | </math> | ||
| + | Последнее выражение является [https://ru.wikipedia.org/wiki/%D0%9F%D0%B5%D1%80%D0%B2%D1%8B%D0%B9_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB первым интегралом] системы <math>(\ref{sys3})</math>, поэтому, учитывая начальные условия <math>S(0) = S_0,\ I(0) = I_0</math>, получается следующее:: | ||
| + | |||
| + | <math> | ||
| + | I + S - \sigma\ln S = I_0 + S_0 - \sigma\ln S_0\ \ \Longrightarrow\ \ I_{max} = I_0 + S_0 - \sigma - \sigma \ln \frac{S_0}{\sigma}. | ||
| + | </math> | ||
| + | <br> | ||
| + | <br> | ||
| + | Помимо максимального числа заражённых полезно знать количество особей, '''так и не переболевших''' за всё время эпидемии. Для этого рассматривается отношение <math>\frac{dS}{dR}</math>:: | ||
| + | <math> | ||
| + | \frac{dS}{dR} = \frac{-\beta SI}{\gamma I} = -\frac{1}{\gamma}S\ \ \Longrightarrow\ \ \sigma\frac{dS}{S}=-dR\ \ \Longrightarrow\ \ \sigma \ln |S| = -R+C\ \ \Longrightarrow\ \ S(t)=C_0 \exp \{-\sigma R\}. | ||
| + | </math> | ||
| + | |||
| + | Как уже было замечено выше, в силу замкнутости популяции <math>I(t)\xrightarrow[t\to\infty]{} 0\ \ \Longrightarrow\ \ S(\infty) + R(\infty) = N.</math> | ||
| + | |||
| + | Тогда можно составить [https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B0%D0%BD%D1%81%D1%86%D0%B5%D0%BD%D0%B4%D0%B5%D0%BD%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5 трансцендентное уравнение]:: | ||
| + | <math>S(\infty) = C_0 \exp \left\{ \frac{S(\infty)-N}{\sigma} \right\},</math> | ||
| + | у которого существует единственное решение, и оно положительно. На рис. 2 можно наблюдать, что со временем количество так и не переболевших особей <math>S(\infty)</math> действительно стабилизируется. | ||
| + | |||
| + | ==Формулировка SEIR-модели== | ||
| + | Существуют более продвинутые модели, учитывающие различные аспекты протекания болезни. Например, '''SEIR-модель''' включает в себя новый, четвёртый ящик <math>E(t)</math> — особи, находящиеся в латентном периоде заболевания, то есть уже заболевшие, но ещё не заразные (англ. ''exposed''). | ||
| + | [[Файл:SEIR-model.png|мини|Рис. 3. Диаграмма эволюции особи популяции в SEIR-модели]] | ||
| + | Описывающая такую динамику система выглядит следующим образом:: | ||
| + | <math> | ||
| + | \begin{equation} | ||
| + | \begin{cases} | ||
| + | \dot{S}(t) = - \beta S(t) I(t),\\ | ||
| + | \dot{E}(t) = \beta S(t) I(t) - \alpha E(t),\\ | ||
| + | \dot{I}(t) = \alpha E(t) - \gamma I(t),\\ | ||
| + | \dot{R}(t) = \gamma I(t). | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | </math> | ||
| + | |||
| + | <br> | ||
| + | ==Список литературы== | ||
| + | # Абрамова В.В. "Лекции по прикладным задачам системного анализа: задачам биоматематики", 2024. | ||
| + | # Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011. | ||
Текущая версия на 01:58, 23 января 2025
Содержание
Математические модели эпидемиологии — динамические системы, описывающие распространение инфекционных популяций среди здоровых.
Не все заболевания рассматриваются в рамках такого исследования: моделируются инфекции, вызываемые микропаразитами. В таком случае можно пренебречь динамикой каждого паразита (в отличие от случая макропаразитов), поскольку заболевание протекает у инфицированных с одинаковым характером. Поэтому обладания информацией о динамике здоровой популяции и заражённой достаточно для анализа модели.
Общая формулировка SIR-модели
Одна из простейших моделей распространения эпидемий — SIR-модель. Это модель ящикового вида, в которой все особи популяции разделяются на группы — "ящики", — внутри которых особи неразличимы.
В SIR-модели все особи поделены на 3 группы:
- \(S(t)\) — подверженные заболеванию особи (от англ. susceptible)
- \(I(t)\) — заражённые особи (от англ. infected)
- \(R(t)\) — переболевшие (от англ. resistant)
Важно отметить, что ящиковая модель, в том числе и SIR-модель, подразумевает собой замкнутую популяцию, в которой не происходят процессы рождаемости и смертности. Поэтому на введённые классы можно выписать ограничение\[ S + I + R = N, \]
где \( N \) — общее число особей популяции.
Замечание. Из замкнутости популяции и характера эволюции особи можно сделать вывод, что с течением времени "ящик" \(I\) заражённых особей станет пустым.
Исследование SIR-модели
Функция инфективности
Для анализа сформулированной модели вводится функция инфективности \(A(\tau)\), которая характеризует вероятность того, что произойдёт заражение индивида при контакте с заражённым индивидом \(\tau\) единиц времени назад.
В общем виде функция инфективности выглядит следующим образом:\[ A(\tau) = \begin{equation} \begin{cases} c \cdot p,\ \ t \in [T_1,\ T_2]\\ 0,\ \ \text{иначе}. \end{cases} \label{sys1} \end{equation} \]
Здесь \(p\) — вероятность заражения, а \(c\) — среднее число контактов в единицу времени. Промежуток времени \(t \in [T_1,\ T_2]\) — окно, в течение которого индивид заразен.
Таким образом, в частном случае \(A(\tau)\) можно ввести так:\[ A(\tau) = \underbrace{\beta N}_{c} \cdot \underbrace{\exp\{ -\gamma\tau \} }_{p},\ \ \beta=const>0,\]
то есть промежуток времени для заражения других особей распределен экспоненциально со средним \(\frac{1}{\gamma}\). Следовательно, средняя длина промежутка времени, в течение которого индивид заразен, равна \(\frac{1}{\gamma}\).
Замечание. Введя подобным образом функцию инфективности, получают, что число контактов растёт линейно с общим объёмом популяции \(N\), что, вообще говоря, является довольно грубым допущением. Однако оно необходимо для упрощения исследования и его наглядности.
Получение аналитического вида SIR-модели
Рассмотрим ещё одну величину \(i(t)\) — число новых заболевших в момент времени \(t\). Таким образом, \(i(t) = -\dot{S}(t)\).
При этом \(i(t)\) можно выразить через уже введённую функцию инфективности:\[i(t) = \frac{S(t)}{N} \int\limits_0^{\infty} A(\tau) i(t-\tau) d\tau.\]
Интеграл в правой части можно трактовать как среднее число "удачных" контактов (т.е. таких, при которых заражение произошло). Причём, в силу выведенной связи на \(i(t)\) и \(S(t)\) можно получить следующее:\[
\begin{equation}
\dot{S}(t) = \frac{S(t)}{N} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau. \label{sys2}
\end{equation}
\]
Далее вводится \(I(t)\) следующим образом:\[ I(t) = -\frac{1}{\beta} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau\ =\ \{s:=t-\tau\}\ =\
-\frac{1}{\beta} \int\limits_{-\infty}^t A(t-s) \dot{S}(s) ds\ =\ \{ \tau:=s\}\ =\ -\frac{1}{\beta} \int\limits_{-\infty}^t A(t-\tau) \dot{S}(\tau) d\tau.\]
С учётом того, что функция инфективности \( A(\tau) \) введена так, что \( \dot{A}(\tau) = -\gamma A(\tau)\), продифференцируем полученное равенство по параметру \(t\):\[
\dot{I}(t) = -\frac{1}{\beta} A(0) \dot{S}(t) + \frac{1}{\beta} \underbrace{A(\infty)}_{= 0}\dot{S}(-\infty) - \frac{1}{\beta} \int\limits_{-\infty}^t \left( -\gamma A(t-\tau) \dot{S}(\tau) \right) d\tau =
\]
\[
= -\frac{\beta N}{\beta}\dot{S}(t) + \gamma\cdot \underbrace{ \frac{1}{\beta} \int\limits_{-\infty}^t A(t-\tau) \dot{S}(\tau) d\tau}_{= - I(t)} = \{ \text{в силу } (\ref{sys2}) \} = \underbrace{-\frac{N S(t)}{N} \int\limits_0^{\infty} A(\tau) \dot{S}(t-\tau) d\tau}_{=\beta SI} - \gamma I(t) = \beta S(t)I(t) - \gamma I(t).
\]
Таким образом, для \(I(t)\) получается следующее уравнение динамики — \( \dot{I}(t) = \beta S(t) I(t) - \gamma I(t) = I(t) \left( \beta S(t) - \gamma \right)\).
Итоговая динамическая система, описывающая SIR-модель, выглядит следующим образом:\[
\begin{equation}
\begin{cases}
\dot{S}(t) = - \beta S(t) I(t),\\
\dot{I}(t) = I(t)\left( \beta S(t) - \gamma \right),\\
\dot{S}(t) + \dot{I}(t) + \dot{R}(t) = 0.
\end{cases} \label{sys3}
\end{equation}
\]
Последнее уравнение системы следует из её замкнутости, упомянутой выше. Причём из системы \((\ref{sys3})\) можно выразить и динамику класса переболевших — \( \dot{R}(t) = \gamma I(t)\).
Анализ SIR-модели
Исследуя полученную динамическую систему \((\ref{sys3})\) SIR-модели, можно заметить, что по переменной \(I\) существует особая точка при \(S = \frac{\gamma}{\beta} := \sigma\). При \( S(t) > \sigma\) число инфицированных растёт, и, наоборот, при \( S(t) < \sigma\) — убывает.
Однако из первого уравнения системы \((\ref{sys3})\ \ \dot{S}(t)\leqslant 0\), поэтому поведение системы разделяется на два существенно разных случая в зависимости от начального количества подверженных заболеванию \( S_0 \):
- \( S_0 < \sigma\ \Longrightarrow\) эпидемии в системе нет, поскольку число заражённых монотонно уменьшается до нуля;
- \( S_0 > \sigma\ \Longrightarrow\) происходит эпидемия в системе.

(а) В системе есть эпидемия с максимальным числом заболевших \(I_{max}\). Параметры \(\sigma = 500,\ \gamma = 5,\) \(N=1000,\ S_0=994,\ I_0=2.\)
(б) В системе не возникает эпидемия, так как \(S_0<\sigma\). Параметры \(\sigma = 800,\ \gamma = 5,\ N=1000,\ S_0=700.\)
Рассмотрим далее случай, когда в системе возникает эпидемия. Важным прикладным результатом исследования такой системы является, например, максимальное количество инфицированных, поскольку это помогает рассчитать эффективное число койко-мест в больницах во время пика эпидемии. На рис. 2 (а) можно наблюдать этот пик, обозначенный за \(I_{max}\). Можно найти его значение аналитически, исследовав \(\frac{dI}{dS}\):\[
\frac{dI}{dS} = \frac{\beta SI - \gamma I}{-\beta SI} = -1 + \frac{\sigma}{S}\ \ \Longrightarrow\ \ I+S-\sigma\ln S = const.
\]
Последнее выражение является первым интегралом системы \((\ref{sys3})\), поэтому, учитывая начальные условия \(S(0) = S_0,\ I(0) = I_0\), получается следующее:\[
I + S - \sigma\ln S = I_0 + S_0 - \sigma\ln S_0\ \ \Longrightarrow\ \ I_{max} = I_0 + S_0 - \sigma - \sigma \ln \frac{S_0}{\sigma}.
\]
Помимо максимального числа заражённых полезно знать количество особей, так и не переболевших за всё время эпидемии. Для этого рассматривается отношение \(\frac{dS}{dR}\):\[
\frac{dS}{dR} = \frac{-\beta SI}{\gamma I} = -\frac{1}{\gamma}S\ \ \Longrightarrow\ \ \sigma\frac{dS}{S}=-dR\ \ \Longrightarrow\ \ \sigma \ln |S| = -R+C\ \ \Longrightarrow\ \ S(t)=C_0 \exp \{-\sigma R\}.
\]
Как уже было замечено выше, в силу замкнутости популяции \(I(t)\xrightarrow[t\to\infty]{} 0\ \ \Longrightarrow\ \ S(\infty) + R(\infty) = N.\)
Тогда можно составить трансцендентное уравнение:\[S(\infty) = C_0 \exp \left\{ \frac{S(\infty)-N}{\sigma} \right\},\] у которого существует единственное решение, и оно положительно. На рис. 2 можно наблюдать, что со временем количество так и не переболевших особей \(S(\infty)\) действительно стабилизируется.
Формулировка SEIR-модели
Существуют более продвинутые модели, учитывающие различные аспекты протекания болезни. Например, SEIR-модель включает в себя новый, четвёртый ящик \(E(t)\) — особи, находящиеся в латентном периоде заболевания, то есть уже заболевшие, но ещё не заразные (англ. exposed).
Описывающая такую динамику система выглядит следующим образом:\[ \begin{equation} \begin{cases} \dot{S}(t) = - \beta S(t) I(t),\\ \dot{E}(t) = \beta S(t) I(t) - \alpha E(t),\\ \dot{I}(t) = \alpha E(t) - \gamma I(t),\\ \dot{R}(t) = \gamma I(t). \end{cases} \end{equation} \]
Список литературы
- Абрамова В.В. "Лекции по прикладным задачам системного анализа: задачам биоматематики", 2024.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.