Преобразование Лапласа: различия между версиями
Janus (обсуждение | вклад) м |
Tochilin (обсуждение | вклад) |
||
| (не показано 25 промежуточных версий 2 участников) | |||
| Строка 8: | Строка 8: | ||
\begin{equation}\label{intLapl} | \begin{equation}\label{intLapl} | ||
| − | \boxed{F(p) = \int\limits^{+\infty}_0 f(t) e^{-pt} dt, \quad p \in \mathbb | + | \boxed{F(p) = \int\limits^{+\infty}_0 f(t) e^{-pt} dt, \quad p=\mu+i \lambda \in \mathbb{C}.} |
\end{equation} | \end{equation} | ||
Правая часть этого выражения называется ''интегралом Лапласа''. | Правая часть этого выражения называется ''интегралом Лапласа''. | ||
| − | Для преобразования Лапласа используется обозначение $$f(t) \supset F(t | + | Для преобразования Лапласа используется обозначение $$f(t) \supset F(t)$$. |
| − | |||
| − | |||
| + | Выясним, при каких условиях существует интеграл Лапласа для заданной функции $$f(t)$$. Будем рассматривать функцию $$f_\mu(t) = e^{-\mu t} f(t)$$, $$\mu \in \mathbb{R}$$. Пусть существуют константы $$A$$, $$\mu_0$$ такие, что $$|f(t)| \le Ae^{\mu_0 t}$$ $$\forall t\ge T$$. Тогда для любого $$\mu > \mu_0$$ $$\exists \int\limits_0^{+\infty} |e^{-\mu t} f(t)|dt < \infty$$. Поставим в соответствие функции $$f_\mu(t)$$ функцию $$F_\mu(t)$$, определяемую как [https://sawiki.cs.msu.ru/index.php/Интегральное_преобразование_Фурье прямое преобразование Фурье] функции $$f_\mu(t)$$: | ||
| + | \[ | ||
| + | F_\mu(t) = \int\limits_0^{+\infty} f_\mu(t) e^{-i\lambda t} dt = \int\limits_0^{+\infty} f(t) e^{-\mu t} e^{-i\lambda t} dt = \left\{\text{обозначим } p = \mu + i\lambda\in \mathbb{C}\right\} = \int\limits_0^{+\infty} f(t) e^{-pt} dt \equiv F(p). | ||
| + | \] | ||
Получаем следующие достаточные условия существования прямого преобразования Лапласа: | Получаем следующие достаточные условия существования прямого преобразования Лапласа: | ||
| − | # | + | # Функция $$f$$ растёт не быстрее показательной функции, т.е. <br/>\begin{equation}\label{growth_cond} |
| − | \begin{equation}\label{growth_cond} | + | \exists A, \mu_0 \text{ такие, что } |f(t)|\le Ae^{\mu_0 t} \quad \forall t\ge T.\end{equation}<br/> |
| − | \exists A, \mu_0 \text{ такие, что } |f(t)|\le Ae^{ | + | # Интеграл $$\int\limits_0^{+\infty}|f(t)| dt$$ существует и конечен. |
| − | \end{equation} | ||
| − | # | ||
=== Обратное преобразование === | === Обратное преобразование === | ||
| Строка 39: | Строка 39: | ||
Рассмотрим обратное преобразование Фурье от функции $$F_\mu(\omega)$$: | Рассмотрим обратное преобразование Фурье от функции $$F_\mu(\omega)$$: | ||
\[ | \[ | ||
| − | f(t) e^{-\mu t} \chi(t) = f_\mu(t) \chi(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F_\mu(\ | + | f(t) e^{-\mu t} \chi(t) = f_\mu(t) \chi(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F_\mu(\lambda) e^{i\lambda t} d\lambda = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F(p) e^{i\lambda t} d\lambda. |
\] | \] | ||
| − | Сделаем замену $$p = \mu + i\ | + | Сделаем замену $$p = \mu + i\lambda$$. Тогда $$d\lambda = \frac{dp}{i}$$, а верхний и нижний пределы интегрирования равны: $$\lambda = +\infty \Rightarrow p = \mu + i\infty$$, $$\lambda = -\infty \Rightarrow p = \mu - i\infty$$. Получаем: |
\[ | \[ | ||
| Строка 50: | Строка 50: | ||
Домножив обе части равенства на $$e^{\mu t}$$, окончательно получим формулу '''обратного преобразования Лапласа''': | Домножив обе части равенства на $$e^{\mu t}$$, окончательно получим формулу '''обратного преобразования Лапласа''': | ||
| − | \ | + | \begin{equation}\label{Mellins_formula} |
\boxed{f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p)e^{pt} dp.} | \boxed{f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p)e^{pt} dp.} | ||
| − | \ | + | \end{equation} |
Правая часть этого выражения называется ''формулой Меллина''. | Правая часть этого выражения называется ''формулой Меллина''. | ||
| Строка 61: | Строка 61: | ||
Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости <math>\mathrm{Re} p > \mu_0</math> и является в этой области аналитической функцией. | Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости <math>\mathrm{Re} p > \mu_0</math> и является в этой области аналитической функцией. | ||
| − | '''Доказательство'''. Докажем, сначала, что интеграл Лапласа \eqref{intLapl} сходится абсолютно в области $$\mathrm{Re} p = \mu > \mu_0$$. В силу общего признака сравнения и условия роста \eqref{growth_cond} получаем, что | + | '''Доказательство'''. Докажем, сначала, что интеграл Лапласа \eqref{intLapl} сходится абсолютно в области $$\mathrm{Re} p = \mu > \mu_0$$. Наименьшее такое число $$\mu_0$$ называют \textit{абсциссой сходимости} преобразования Лапласа. |
| + | |||
| + | В силу общего признака сравнения и условия роста \eqref{growth_cond} получаем, что | ||
\[ | \[ | ||
| Строка 73: | Строка 75: | ||
то есть интеграл Лапласа сходится абсолютно. | то есть интеграл Лапласа сходится абсолютно. | ||
| − | Докажем теперь существование производной несобственного интеграла \eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$\mathrm{Re}\,p > \mu_0$$ интеграла | + | Докажем теперь существование производной несобственного интеграла \eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$\mathrm{Re}\,p \ge \mu_1$$ (для любого $$\mu_1 > \mu_0$$) интеграла |
\[ | \[ | ||
| − | F'(p) = J(p) = \int\limits_0^{+\infty} (-t) f(t) e^{(\mu + i\omega)t} dt | + | F'(p) = J(p) = \int\limits_0^{+\infty} (-t) f(t) e^{(\mu + i\omega)t} dt. |
\] | \] | ||
| Строка 87: | Строка 89: | ||
<u>Замечание</u>. Из неравенства \eqref{int_bounds} вытекает, что $$\lim\limits_{\mu \to +\infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)\to 0$$ при $$p \to \infty$$, оставаясь внутри угла $$-\frac{\pi}{2} + \delta < \arg p < \frac{\pi}{2} - \delta$$, где $$\delta$$ — сколь угодно малое положительное число. | <u>Замечание</u>. Из неравенства \eqref{int_bounds} вытекает, что $$\lim\limits_{\mu \to +\infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)\to 0$$ при $$p \to \infty$$, оставаясь внутри угла $$-\frac{\pi}{2} + \delta < \arg p < \frac{\pi}{2} - \delta$$, где $$\delta$$ — сколь угодно малое положительное число. | ||
| − | |||
== Элементарные преобразования == | == Элементарные преобразования == | ||
| + | |||
| + | Будем обозначать за $$F(p),\ G(p)$$ изображение по Лапласу функций $$f(t),\ g(t)$$. Выпишем таблицу основных преобразований: | ||
{| class="wikitable" style="margin: auto;" | {| class="wikitable" style="margin: auto;" | ||
|- | |- | ||
| − | ! scope="col"| $$f | + | ! scope="col"| $$f(t)$$ |
! scope="col"| $$F(t)$$ | ! scope="col"| $$F(t)$$ | ||
|- | |- | ||
| − | | \[ | + | | \[\chi(t)\] |
| \[\frac{1}{p}\] | | \[\frac{1}{p}\] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ e^{\beta t} \] | + | | \[ \chi(t) e^{\beta t} \] |
| \[ \frac{1}{p-\beta} \] | | \[ \frac{1}{p-\beta} \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ | + | | \[ \chi(t) g(t)e^{\beta t} \] |
| − | | \[ | + | | \[ G(p-\beta) \] |
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ | + | | \[ \chi(t) g(t)e^{-\beta t} \] |
| − | | \[ | + | | \[ G(p+\beta) \] |
|- | |- | ||
| − | | \[ t^\alpha e^{\beta t} \] | + | | \[ \chi(t) t^\alpha e^{\beta t} \] |
| \[ \frac{\Gamma(\alpha + 1)}{(p-\beta)^{\alpha + 1}} \] | | \[ \frac{\Gamma(\alpha + 1)}{(p-\beta)^{\alpha + 1}} \] | ||
|- | |- | ||
| − | | \[ t^n, n\in\mathbb{N} \] | + | | \[ \chi(t) t^n, n\in\mathbb{N} \] |
| \[ \frac{n!}{p^{n+1}} \] | | \[ \frac{n!}{p^{n+1}} \] | ||
|- | |- | ||
| − | | \[ t^\alpha, \alpha\in\mathbb{R} \] | + | | \[ \chi(t) t^\alpha, \alpha\in\mathbb{R} \] |
| \[ \frac{\Gamma(\alpha+1)}{p^{\alpha+1}} \] | | \[ \frac{\Gamma(\alpha+1)}{p^{\alpha+1}} \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ \sin \beta t \] | + | | \[ \chi(t) \sin \beta t \] |
| \[ \frac{\beta}{p^2+\beta^2} \] | | \[ \frac{\beta}{p^2+\beta^2} \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ \cos \beta t \] | + | | \[ \chi(t) \cos \beta t \] |
| \[ \frac{p}{p^2+\beta^2} \] | | \[ \frac{p}{p^2+\beta^2} \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ t^\alpha \sin \beta t \] | + | | \[ \chi(t) t^\alpha \sin \beta t \] |
| \[ \frac{\Gamma(\alpha + 1)}{2i}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} - \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] | | \[ \frac{\Gamma(\alpha + 1)}{2i}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} - \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ t^\alpha \cos \beta t \] | + | | \[ \chi(t) t^\alpha \cos \beta t \] |
| \[ \frac{\Gamma(\alpha + 1)}{2}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} + \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] | | \[ \frac{\Gamma(\alpha + 1)}{2}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} + \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] | ||
|- | |- | ||
| − | | \[ \ | + | | \[ \chi(t) \mathrm{sh} t \] |
| \[ \frac{\beta}{p^2-\beta^2} \] | | \[ \frac{\beta}{p^2-\beta^2} \] | ||
|- | |- | ||
| − | | \[ \ | + | | \[ \chi(t) \mathrm{ch} t \] |
| \[ \frac{p}{p^2-\beta^2} \] | | \[ \frac{p}{p^2-\beta^2} \] | ||
|- | |- | ||
| − | | \[ t^\alpha \ | + | | \[ \chi(t) t^\alpha \mathrm{sh} t \] |
| \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} - \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] | | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} - \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] | ||
|- | |- | ||
| − | | \[ t^\alpha \ | + | | \[ \chi(t) t^\alpha \mathrm{ch} t \] |
| \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} + \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] | | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} + \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] | ||
|-bgcolor="#D3D3D3" | |-bgcolor="#D3D3D3" | ||
| − | | \[ \delta \] | + | | \[ \delta(t) \] |
| \[ 1 \] | | \[ 1 \] | ||
|} | |} | ||
| Строка 149: | Строка 152: | ||
# Пусть $$f(t)=1$$.<br/> \[ | # Пусть $$f(t)=1$$.<br/> \[ | ||
\int\limits_0^{+\infty} t e^{-pt} dt = \left. -\frac{1}{p} e^{-pt} \right|^{+\infty}_0 = \frac{1}{p}. | \int\limits_0^{+\infty} t e^{-pt} dt = \left. -\frac{1}{p} e^{-pt} \right|^{+\infty}_0 = \frac{1}{p}. | ||
| − | \] <br/> Легко видеть, что данный интеграл сходится при любом $$\mu>0$$ | + | \] <br/> Легко видеть, что данный интеграл сходится при любом $$\mu>0$$. |
# Пусть теперь $$f(t) \supset F(p)$$. <br/> \[ | # Пусть теперь $$f(t) \supset F(p)$$. <br/> \[ | ||
\int\limits_0^{+\infty} f(t) e^{(\beta-p)t} dt = F(p-\beta). | \int\limits_0^{+\infty} f(t) e^{(\beta-p)t} dt = F(p-\beta). | ||
| Строка 159: | Строка 162: | ||
\] | \] | ||
# Рассмотрим функции $$\chi(t) t^\alpha \cos \beta t$$ и $$\chi(t) t^\alpha \sin \beta t$$. По формуле Эйлера: \[ | # Рассмотрим функции $$\chi(t) t^\alpha \cos \beta t$$ и $$\chi(t) t^\alpha \sin \beta t$$. По формуле Эйлера: \[ | ||
| − | \cos \beta t = \frac{e^{i\beta t} + e^{-i\beta t}}{2}, \quad \sin \beta t = \frac{e^{i\beta t} - e^{-i\beta t}}{2} | + | \cos \beta t = \frac{e^{i\beta t} + e^{-i\beta t}}{2}, \quad \sin \beta t = \frac{e^{i\beta t} - e^{-i\beta t}}{2}. |
\] <br/> Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций. <br/> Аналогично выводятся формулы для гиперболических тригонометрических функций: \[ | \] <br/> Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций. <br/> Аналогично выводятся формулы для гиперболических тригонометрических функций: \[ | ||
| − | \ | + | \mathrm{sh} x = \frac{e^x - e^{-x}}{2}, \quad \mathrm{ch} x = \frac{e^x + e^{-x}}{2}. |
\] | \] | ||
| Строка 167: | Строка 170: | ||
Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд. | Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд. | ||
| + | |||
| + | === Линейность === | ||
| + | |||
| + | Для любых $$\alpha,\ \beta \in \mathbb{C}$$ справедливо: | ||
| + | |||
| + | \[ | ||
| + | \alpha f(t) + \beta g(t) \supset \alpha F(p) + \beta G(p). | ||
| + | \] | ||
| + | |||
| + | Это соотношение является прямым следствием линейности преобразования Фурье. | ||
| + | |||
| + | === Масштабируемость === | ||
| + | \[ | ||
| + | \begin{matrix} \dfrac{1}{a} f\left( \dfrac{t}{a} \right) \supset F(pa) \\ | ||
| + | f(ta) \supset \dfrac{1}{a} F\left( \dfrac{p}{a} \right) \end{matrix} | ||
| + | \quad \forall a>0. | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Рассмотрим преобразование Лапласа функции $$f\left( \frac{t}{a} \right)$$: | ||
| + | \[ | ||
| + | \int\limits_0^{+\infty} f\left( \dfrac{t}{a} \right) e^{-pt} dt = \left\{ \begin{matrix} z = at \\ dz = adt \end{matrix} \right\} = \int\limits_0^{+\infty} f(z) e^{-paz} a\,dz = aF(pa). | ||
| + | \] | ||
| + | |||
| + | Аналогично доказывается вторая формула. $$\blacksquare$$ | ||
| + | |||
| + | === Сдвиг №1 === | ||
| + | [[File:LT_ShiftNo1.png|frame|left|Запаздывающий сигнал.]] | ||
| + | |||
| + | Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо: | ||
| + | \[ | ||
| + | \chi(t-\tau)f(t-\tau) \supset e^{-p\tau}F(p). | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Применим преобразование Лапласа к функции $$\chi(t-\tau) f(t-\tau)$$. Сделав замену переменной $$\xi = t-a$$, получим | ||
| + | \[ | ||
| + | \int\limits_\tau^{+\infty} f(t-\tau) e^{-pt} dt = \int_0^{+\infty} f(\xi) e^{-p(\tau+\xi)} d\xi = e^{-p\tau} F(\xi). \quad \blacksquare | ||
| + | \] | ||
| + | |||
| + | === Сдвиг №2 === | ||
| + | [[File:LT_ShiftNo2.png|frame|right|Оригинальный и сдвинутый сигналы.]] | ||
| + | |||
| + | Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо: | ||
| + | |||
| + | \[ | ||
| + | \chi(t) f(t+a) \supset e^{pa} \left( F(p) - \int\limits_0^a f(\xi) e^{-p\xi} d\xi \right). | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Найдём преобразование Лапласа для функции $$\chi(t) f(t+a)$$: | ||
| + | \[ | ||
| + | \int\limits_0^{+\infty} f(t+a)e^{-pt} dt = \int\limits_0^{+\infty} e^{-p(\xi-a)} d\xi - \int\limits_0^a f(\xi) e^{-p(\xi-a)} d\xi. \quad \blacksquare | ||
| + | \] | ||
| + | |||
| + | Заметим, что вычитаемое в этой формуле соответствует утерянной части сигнала. | ||
| + | |||
| + | === Дифференцирование оригинала === | ||
| + | Если функция $$f(t) \in C'(0, +\infty)$$ и она удовлетворяет достаточным условиям существования прямого преобразования Лапласа, тогда выполнено следующее соотношение: | ||
| + | \begin{equation}\label{LT_Deriv} | ||
| + | f'(t) \supset pF(p) -f(0+0). | ||
| + | \end{equation} | ||
| + | |||
| + | В общем случае: если $$f(t) \in C^{(k)}(0,+\infty)$$ и выполнены достаточные условия существования прямого преобразования, то | ||
| + | \begin{equation}\label{LT_Derivk} | ||
| + | f^{(k)}(t) \supset p^k F(p) - p^{k-1} f(0+0) - p^{k-2} f'(0+0) - \dots - pf^{(k-2)}(0+0) - f^{(k-1)}(0+0). | ||
| + | \end{equation} | ||
| + | |||
| + | '''Доказательство'''. Посчитаем преобразование Лапласа от функции $$f'(t)$$. Используя интегрирование по частям, получаем: | ||
| + | \[ | ||
| + | \int\limits_0^{+\infty} f'(t) e^{-pt} dt = f(t) e^{-pt} \bigg|_0^{+\infty} - \int\limits_0^{+\infty} f(t) (-p) e^{-pt} dt = 0 - f(0+0) + pF(p). | ||
| + | \] | ||
| + | |||
| + | Далее найдём изображение второй производной, дважды применив формулу \eqref{LT_Deriv}: | ||
| + | \[ | ||
| + | f''(t) = \left( f(t) \right)' \supset p\Bigl( pF(p) - f(0+0) \Bigr) - f'(0+0) = p^2 F(p) - pf(0+0) - f'(0+0). | ||
| + | \] | ||
| + | |||
| + | Далее, по методу математической индукции, находим: | ||
| + | \[ | ||
| + | f^{(k)} = \left( f^{(k-1)}(t) \right) \supset p \left( p^{k-1} F(p) -\sum\limits_{l=1}^{k-2} p^{k-2-l} f^{(l)}(0+0) \right) - f^{(k-1)}(0+0). | ||
| + | \] | ||
| + | |||
| + | Раскрывая скобки, перейдём к выражению \eqref{LT_Derivk}. $$\blacksquare$$ | ||
| + | |||
| + | === Дифференцирование изображения === | ||
| + | \[ | ||
| + | (-t)^k f(t) \supset F^{(k)} (p). | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Как уже было установлено, изображение $$F(p)$$ является аналитической функцией в полуплоскости $$\mathrm{Re}\,p = \mu > \mu_0$$, а значит её можно дифференцировать по $$p$$ как интеграл, зависящий от параметра. Применим к формуле \eqref{intLapl} $$k$$-кратное дифференцирование: | ||
| + | \[ | ||
| + | F^{(k)}(p) = \int\limits_0^{+\infty} (-t)^k f(t) e^{-pt} dt. \quad \blacksquare | ||
| + | \] | ||
| + | |||
| + | === Интегрирование оригинала === | ||
| + | |||
| + | \[ | ||
| + | \int\limits_0^t f(\tau) d\tau \supset \dfrac{F(p)}{p}. | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. По формуле \eqref{intLapl} получаем, что | ||
| + | \[ | ||
| + | F(p) = \int\limits_0^{+\infty} e^{-pt} f(t) dt = \int\limits_0^{+\infty} e^{-pt} d\left( \int\limits_0^t f(\tau) d\tau \right). | ||
| + | \] | ||
| + | Далее применим формулу интегрирования по частям: | ||
| + | \[ | ||
| + | \int\limits_0^{+\infty} e^{-pt} d\left( \int\limits_0^t f(\tau) d\tau \right) = e^{-pt} \int\limits_0^t f(t) dt \Bigg|_{t=0}^{+\infty} + p\int_0^{+\infty} e^{-pt} dt \int\limits_0^t f(\tau) d\tau = p\int\limits_0^{+\infty} e^{-pt} dt\int\limits_0^t f(\tau) d\tau. | ||
| + | \] | ||
| + | Так как функция $$f(t)$$ возрастает не быстрее показательной, то мы можем избавиться от первого слагаемого. $$\blacksquare$$ | ||
| + | |||
| + | === Интегрирование образа === | ||
| + | |||
| + | Если интеграл $$\int_p^\infty F(\xi) d\xi$$ сходится по любому пути, целиком лежащему в области $$\mathrm{Re}\,p > \mu_0$$, то он является изображением функции $$f(t)/t$$, т.е. | ||
| + | \[ | ||
| + | \dfrac{f(t)}{t} \supset \int\limits_p^\infty F(\xi) d\xi. | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Согласно \eqref{intLapl}: | ||
| + | \begin{equation}\label{double_int} | ||
| + | \int_p^\infty F(\xi) d\xi = \int_p^\infty d\xi \int\limits_0^{+\infty} f(t) e^{-\xi t} dt. | ||
| + | \end{equation} | ||
| + | |||
| + | Предположим, что путь интегрирования $$(p,\infty)$$ целиком лежит в полуплоскости $$\mathrm{Re}\,\xi \ge \mu > \mu_0$$. Дадим оценку внутреннего интеграла: | ||
| + | \[ | ||
| + | \left| \int\limits_0^{+\infty} f(t) e^{-qt} dt \right| < A \int\limits_0^{+\infty} e^{-(\mu-\mu_0)t} dt = \dfrac{M}{\mu-\mu_0} < \infty. | ||
| + | \] | ||
| + | |||
| + | Отсюда по достаточному признаку Вейерштрасса следует равномерная сходимость данного интеграла по параметру $$\xi$$ в области $$\mathrm{Re}\,p > \mu_0$$. Тогда в интеграле \eqref{double_int} можно сменить порядок интегрирования: | ||
| + | \[ | ||
| + | \int\limits_p^\infty F(\xi) d\xi = \int\limits_0^{+\infty} f(t) dt \int\limits_p^\infty e^{-\xi t} d\xi = \int_0^{+\infty} f(t) \dfrac{e^{-pt}}{t} dt. \quad \blacksquare | ||
| + | \] | ||
| + | |||
| + | === Свёртка === | ||
| + | |||
| + | Напомним, что свёрткой функций $$f(t)$$ и $$g(t)$$ называют функцию вида: | ||
| + | \[ | ||
| + | f(t)*g(t) \equiv \int\limits_{-\infty}^{+\infty} f(\tau)g(t-\tau) d\tau = \int\limits_{-\infty}^{+\infty} g(\tau) f(t-\tau) d\tau. | ||
| + | \] | ||
| + | Для функций-оригиналов с учётом того, что $$f(t)\equiv 0$$ и $$g(t)\equiv 0$$ при $$t<0$$ получаем, что | ||
| + | \begin{equation}\label{convolution} | ||
| + | f(t)*g(t) \equiv \int\limits_0^t f(\tau)g(t-\tau) d\tau. | ||
| + | \end{equation} | ||
| + | |||
| + | Свёртка оригиналов соответствует произведению изображений: | ||
| + | \[ | ||
| + | (f*g)(t) \supset F(p) \cdot G(p). | ||
| + | \] | ||
| + | |||
| + | '''Доказательство'''. Сначала покажем, что свёртка оригиналов \eqref{convolution} является оригиналом, то есть выполняются достаточные условия существования прямого образования Лапласа. Очевидно, что $$f(t)*g(t) \equiv 0$$ при $$t<0$$. Покажем, что свёртка имеет скорость сходимости не выше экспоненциальной. Так как оригиналы удовлетворяют следующим условиям: | ||
| + | \[ | ||
| + | |f(t)| < A e^{\mu_0 t}, \quad |g(t)| < B e^{\mu_1 t}, | ||
| + | \] | ||
| + | то мы имеем следующую оценку абсолютной величины свёртки: | ||
| + | \[ | ||
| + | |f(t) * g(t)| = \left| \int\limits_0^t f(\tau) g(t-\tau) d\tau \right| < AB \int\limits_0^t e^{\mu_0 \tau} e^{\mu_1 (t-\tau)} d\tau \le AB te^{\mu t}, | ||
| + | \] | ||
| + | где $$\mu = \max\{ \mu_0, \mu_1 \}$$. Отсюда получаем, что $$|f(t) * g(t)| < C e^{(\mu + \varepsilon) t}$$. | ||
| + | |||
| + | Докажем теперь справедливость формулы для образа свёртки. Согласно \eqref{intLapl}: | ||
| + | \[ | ||
| + | f(t) * g(t) \supset \int\limits_0^{+\infty} e^{-pt} dt \int_0^t f(\tau) g(t-\tau) d\tau. | ||
| + | \] | ||
| + | |||
| + | Поменяем порядок интегрирования в двойном интеграле: | ||
| + | \[ | ||
| + | \int\limits_0^{+\infty} e^{-pt} dt \int_0^t f(\tau) g(t-\tau) d\tau = \int_0^{+\infty} f(\tau) d\tau \int\limits_\tau^{+\infty}g(t-\tau) e^{-pt} dt = \Bigl\{ t-\tau = \theta \Bigr\} = \int\limits_0^{\infty} f(\tau) d\tau \int\limits_0^{+\infty} g(\theta) e^{-p(\theta + \tau)} d\theta. \quad \blacksquare | ||
| + | \] | ||
| + | |||
| + | === Периодическая функция === | ||
| + | |||
| + | Пусть $$f(t)$$ — периодическая функция с периодом $$T>0$$. | ||
| + | |||
| + | \[ | ||
| + | \int\limits_0^{+\infty} f(t) e^{-pt} dt = \sum\limits_{k=1}^{+\infty} \int_{(k-1)T}^{kT} f(t) e^{-pt} dt = \left\{ t = (k-1)T + s \right\} = \sum\limits_{k=1}^{+\infty} \int_0^T f(s) e^{-ps} e^{-p(k-1)T} ds = \left( \sum\limits_{k=1}^{+\infty} e^{-p(k-1)T} \right) \int\limits_0^T f(s) e^{-ps} ds = \dfrac{1}{1-e^{-pT}} \int\limits_0^T f(s) e^{-ps} ds, | ||
| + | \] | ||
| + | то есть в случае периодической функции достаточно посчитать интеграл Лапласа на одном периоде. | ||
| + | |||
| + | == Вычисление обратного преобразования Лапласа == | ||
| + | |||
| + | === Общий случай === | ||
| + | [[File:Analit_pict.PNG|300px|thumb|right|.]] | ||
| + | |||
| + | Рассмотрим формулу Меллина \eqref{Mellins_formula}: | ||
| + | \[ | ||
| + | f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp. | ||
| + | \] | ||
| + | |||
| + | В области $$\mu > \mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, \dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} \overset{\Omega_R}{\underset{\R \to +\infty}{\rightrightarrows}} 0$$. Отсюда получаем: | ||
| + | \[ | ||
| + | f(t)\chi(t) = \frac{1}{2\pi i } \cdot 2\pi i \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) = \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i). | ||
| + | \] | ||
| + | |||
| + | === Рациональный образ === | ||
| + | |||
| + | Напомним, что $$\delta(t) \supset 1$$. Используя элементарные преобразования и свойства преобразования Лапласа можем выписать следующие выражения: | ||
| + | \begin{equation}\label{delta} | ||
| + | \delta^{(k)}(t) \supset p^k, \quad \delta(t-\alpha) \supset e^{-p\alpha}, \quad \delta^{(k)}(t-\alpha) \supset e^{-p\alpha} p^k. | ||
| + | \end{equation} | ||
| + | |||
| + | Пусть функция $$F(p)$$ — рациональная, то есть она имеет вид $$F(p) = \dfrac{Q(p)}{P(p)}$$, где $$Q(p)$$ и $$P(p)$$ — многочлены от переменной $$p$$. | ||
| + | * Пусть $$\deg Q \ge \deg P$$. Тогда можем выполнить деление многочленов и воспользоваться выражениями \eqref{delta}. | ||
| + | * Пусть $$\deg Q \le deg P$$. Тогда эту дробь можно разложить в следующую сумму: | ||
| + | \[ | ||
| + | \dfrac{Q(p)}{P(p)} = \dfrac{A_{1m_1}}{(p-\alpha_1)^{m_1}} + \dfrac{A_{1(m_1-1)}}{(p-\alpha_1)^{m_1-1}} + \dots + \dfrac{A_{11}}{p-\alpha_1} + \dfrac{A_{2m_2}}{(p-\alpha_2)^{m_2}} + \dots + \dfrac{A_{21}}{p-\alpha_2} + \dots + \dfrac{B_{11}(p-\eta) + C_{11}}{p^2 + \beta_1 p + \gamma_1} + \dots + \dfrac{B_{1n_1}p + C_{1n_1}}{(p^2 + \beta_1 p + \gamma_1)^{n_1}} + \dots . | ||
| + | \] | ||
| + | |||
| + | Теперь, пользуясь линейностью преобразования Лапласа, можем искать прообразы каждого слагаемого по-отдельности. В случае, если в знаменателе стоит выражение степени $$k>1$$, нужно воспользоваться свойством дифференцирования для понижения степени. Иначе, используя элементарные преобразования, получаем, что | ||
| + | \[ | ||
| + | A_{11} e^{\alpha_1 t} \supset \dfrac{A_{11}}{p-\alpha_1}. | ||
| + | \] | ||
| + | |||
| + | Для дробей с квадратным трёхчленом в знаменателе воспользуемся методом выделения полного квадрата: | ||
| + | \[ | ||
| + | \dfrac{B_{11}p + C_{11}}{p^2 + \beta_1 p + \gamma_1} = \dfrac{B_{11}(p-\eta) + \left( C_{11} + B_{11}\eta \right)}{(p-\eta)^2 + w^2)} = \dfrac{B_{11}(p-\eta)}{(p-\eta)^2 + w^2)} + \dfrac{C_{11} + B_{11}\eta}{(p-\eta)^2 + w^2} \supset B_{11}e^{\eta t} \cos wt + \tilde{C} e^{\eta t} \sin wt . | ||
| + | \] | ||
Текущая версия на 16:32, 17 ноября 2024
Преобразование Лапласа — интегральное преобразование, связывающее функцию $$F(p)$$ комплексного переменного (изображение) с функцией $$f(t)$$ вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование
Преобразованием Лапласа действительнозначной функции $$f(t)$$ называется функция $$F(p)$$ комплексной переменной такая, что
\begin{equation}\label{intLapl} \boxed{F(p) = \int\limits^{+\infty}_0 f(t) e^{-pt} dt, \quad p=\mu+i \lambda \in \mathbb{C}.} \end{equation}
Правая часть этого выражения называется интегралом Лапласа.
Для преобразования Лапласа используется обозначение $$f(t) \supset F(t)$$.
Выясним, при каких условиях существует интеграл Лапласа для заданной функции $$f(t)$$. Будем рассматривать функцию $$f_\mu(t) = e^{-\mu t} f(t)$$, $$\mu \in \mathbb{R}$$. Пусть существуют константы $$A$$, $$\mu_0$$ такие, что $$|f(t)| \le Ae^{\mu_0 t}$$ $$\forall t\ge T$$. Тогда для любого $$\mu > \mu_0$$ $$\exists \int\limits_0^{+\infty} |e^{-\mu t} f(t)|dt < \infty$$. Поставим в соответствие функции $$f_\mu(t)$$ функцию $$F_\mu(t)$$, определяемую как прямое преобразование Фурье функции $$f_\mu(t)$$: \[ F_\mu(t) = \int\limits_0^{+\infty} f_\mu(t) e^{-i\lambda t} dt = \int\limits_0^{+\infty} f(t) e^{-\mu t} e^{-i\lambda t} dt = \left\{\text{обозначим } p = \mu + i\lambda\in \mathbb{C}\right\} = \int\limits_0^{+\infty} f(t) e^{-pt} dt \equiv F(p). \] Получаем следующие достаточные условия существования прямого преобразования Лапласа:
- Функция $$f$$ растёт не быстрее показательной функции, т.е.
\begin{equation}\label{growth_cond} \exists A, \mu_0 \text{ такие, что } |f(t)|\le Ae^{\mu_0 t} \quad \forall t\ge T.\end{equation} - Интеграл $$\int\limits_0^{+\infty}|f(t)| dt$$ существует и конечен.
Обратное преобразование
Будем рассматривать физически реализуемую функцию $$\chi(t)f_\mu(t)$$, где функция $$\chi(t)$$ — функция Хевисайда: \[ \chi(t) = \left\{\begin{align*} 1,\ &t\ge0,\\ 0,\ &t<0. \end{align*}\right. \]
В этом случае $$t$$ может иметь смысл времени, поэтому получаем, что функция $$f(t)\chi(t)$$ задана только на положительной полуоси $$t\ge0$$.
Рассмотрим обратное преобразование Фурье от функции $$F_\mu(\omega)$$: \[ f(t) e^{-\mu t} \chi(t) = f_\mu(t) \chi(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F_\mu(\lambda) e^{i\lambda t} d\lambda = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F(p) e^{i\lambda t} d\lambda. \]
Сделаем замену $$p = \mu + i\lambda$$. Тогда $$d\lambda = \frac{dp}{i}$$, а верхний и нижний пределы интегрирования равны: $$\lambda = +\infty \Rightarrow p = \mu + i\infty$$, $$\lambda = -\infty \Rightarrow p = \mu - i\infty$$. Получаем:
\[ f(t) e^{-\mu t} \chi(t) = \frac{1}{2\pi i} e^{-\mu t} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p) e^{pt} dp \quad \forall \mu > \tilde{\mu}. \]
Домножив обе части равенства на $$e^{\mu t}$$, окончательно получим формулу обратного преобразования Лапласа:
\begin{equation}\label{Mellins_formula} \boxed{f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p)e^{pt} dp.} \end{equation}
Правая часть этого выражения называется формулой Меллина.
Теорема об области существовании изображения
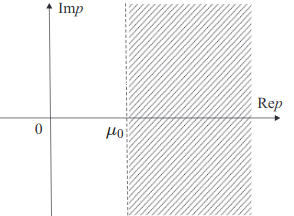
Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости \(\mathrm{Re} p > \mu_0\) и является в этой области аналитической функцией.
Доказательство. Докажем, сначала, что интеграл Лапласа \eqref{intLapl} сходится абсолютно в области $$\mathrm{Re} p = \mu > \mu_0$$. Наименьшее такое число $$\mu_0$$ называют \textit{абсциссой сходимости} преобразования Лапласа.
В силу общего признака сравнения и условия роста \eqref{growth_cond} получаем, что
\[ \left|\int\limits_0^{+\infty} f(t) e^{pt} dt\right| \le \int\limits_0^{+\infty} |f(t)| e^{-\mu t} dt < A \int\limits_0^{+\infty} e^{-(\mu-\mu_0)t} dt. \]
Итак, для $$\mu>\mu_0$$: \begin{equation}\label{int_bounds} \left| \int\limits_0^{+\infty} f(t) e^{-pt} dt \right| < \frac{A}{\mu-\mu_0}, \end{equation} то есть интеграл Лапласа сходится абсолютно.
Докажем теперь существование производной несобственного интеграла \eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$\mathrm{Re}\,p \ge \mu_1$$ (для любого $$\mu_1 > \mu_0$$) интеграла \[ F'(p) = J(p) = \int\limits_0^{+\infty} (-t) f(t) e^{(\mu + i\omega)t} dt. \]
Выберем произвольное положительное действительное число $$\mu_1$$ такое, что $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. Тогда, в соответствии с признаком Вейерштрасса равномерной сходимости получаем, что
\[ |J(p)| \le \int\limits_0^{+\infty} t |f(t)| e^{-\mu_1 t} dt < A\int\limits_0^{+\infty} t e^{-(\mu_1-\mu_0)t} dt = \frac{A}{(\mu_1-\mu_0)^2} < \infty, \]
что и доказывает возможность дифференцирования интеграла \eqref{intLapl} по параметру $$p$$ в области $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. В силу произвольности выбора $$\mu_1$$ мы доказали аналитичность изображения в области $$\mathrm{Re}\,p > \mu_0$$. $$\blacksquare$$
Замечание. Из неравенства \eqref{int_bounds} вытекает, что $$\lim\limits_{\mu \to +\infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)\to 0$$ при $$p \to \infty$$, оставаясь внутри угла $$-\frac{\pi}{2} + \delta < \arg p < \frac{\pi}{2} - \delta$$, где $$\delta$$ — сколь угодно малое положительное число.
Элементарные преобразования
Будем обозначать за $$F(p),\ G(p)$$ изображение по Лапласу функций $$f(t),\ g(t)$$. Выпишем таблицу основных преобразований:
| $$f(t)$$ | $$F(t)$$ |
|---|---|
| \[\chi(t)\] | \[\frac{1}{p}\] |
| \[ \chi(t) e^{\beta t} \] | \[ \frac{1}{p-\beta} \] |
| \[ \chi(t) g(t)e^{\beta t} \] | \[ G(p-\beta) \] |
| \[ \chi(t) g(t)e^{-\beta t} \] | \[ G(p+\beta) \] |
| \[ \chi(t) t^\alpha e^{\beta t} \] | \[ \frac{\Gamma(\alpha + 1)}{(p-\beta)^{\alpha + 1}} \] |
| \[ \chi(t) t^n, n\in\mathbb{N} \] | \[ \frac{n!}{p^{n+1}} \] |
| \[ \chi(t) t^\alpha, \alpha\in\mathbb{R} \] | \[ \frac{\Gamma(\alpha+1)}{p^{\alpha+1}} \] |
| \[ \chi(t) \sin \beta t \] | \[ \frac{\beta}{p^2+\beta^2} \] |
| \[ \chi(t) \cos \beta t \] | \[ \frac{p}{p^2+\beta^2} \] |
| \[ \chi(t) t^\alpha \sin \beta t \] | \[ \frac{\Gamma(\alpha + 1)}{2i}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} - \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] |
| \[ \chi(t) t^\alpha \cos \beta t \] | \[ \frac{\Gamma(\alpha + 1)}{2}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} + \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] |
| \[ \chi(t) \mathrm{sh} t \] | \[ \frac{\beta}{p^2-\beta^2} \] |
| \[ \chi(t) \mathrm{ch} t \] | \[ \frac{p}{p^2-\beta^2} \] |
| \[ \chi(t) t^\alpha \mathrm{sh} t \] | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} - \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] |
| \[ \chi(t) t^\alpha \mathrm{ch} t \] | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} + \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] |
| \[ \delta(t) \] | \[ 1 \] |
Приведём доказательства для некоторых из этих формул.
- Пусть $$f(t)=1$$.
\[ \int\limits_0^{+\infty} t e^{-pt} dt = \left. -\frac{1}{p} e^{-pt} \right|^{+\infty}_0 = \frac{1}{p}. \]
Легко видеть, что данный интеграл сходится при любом $$\mu>0$$. - Пусть теперь $$f(t) \supset F(p)$$.
\[ \int\limits_0^{+\infty} f(t) e^{(\beta-p)t} dt = F(p-\beta). \] - Найдём преобразование Лапласа для функции $$f(t) = \chi(t) t^\alpha$$, $$\alpha > 0$$.
\[ \forall p\in\mathbb{R} : \int\limits_0^{+\infty} t^\alpha e^{-\pt} dt = \left\{ \begin{matrix} pt = s \\ ds = pdt \end{matrix} \right\} = \int\limits_0^{+\infty} \left( \frac{s}{p} \right)^\alpha e^{-s} \frac{1}{p} ds = \frac{1}{p^{\alpha + 1}} \int\limits_0^{+\infty} s^\alpha e^{-s} ds = \frac{1}{p^{\alpha + 1}} \Gamma(\alpha + 1). \]
Эту функцию можно аналитически продолжить на всю комплексную плоскость, т.е. \[ \forall p\in\mathbb{C} : \chi(t) t^\alpha \supset \frac{\Gamma(\alpha + 1)}{p^{\alpha + 1}} \quad \forall \alpha > 0. \] - Рассмотрим функции $$\chi(t) t^\alpha \cos \beta t$$ и $$\chi(t) t^\alpha \sin \beta t$$. По формуле Эйлера: \[
\cos \beta t = \frac{e^{i\beta t} + e^{-i\beta t}}{2}, \quad \sin \beta t = \frac{e^{i\beta t} - e^{-i\beta t}}{2}.
\]
Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций.
Аналогично выводятся формулы для гиперболических тригонометрических функций: \[ \mathrm{sh} x = \frac{e^x - e^{-x}}{2}, \quad \mathrm{ch} x = \frac{e^x + e^{-x}}{2}. \]
Свойства преобразования Лапласа
Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд.
Линейность
Для любых $$\alpha,\ \beta \in \mathbb{C}$$ справедливо:
\[ \alpha f(t) + \beta g(t) \supset \alpha F(p) + \beta G(p). \]
Это соотношение является прямым следствием линейности преобразования Фурье.
Масштабируемость
\[ \begin{matrix} \dfrac{1}{a} f\left( \dfrac{t}{a} \right) \supset F(pa) \\ f(ta) \supset \dfrac{1}{a} F\left( \dfrac{p}{a} \right) \end{matrix} \quad \forall a>0. \]
Доказательство. Рассмотрим преобразование Лапласа функции $$f\left( \frac{t}{a} \right)$$: \[ \int\limits_0^{+\infty} f\left( \dfrac{t}{a} \right) e^{-pt} dt = \left\{ \begin{matrix} z = at \\ dz = adt \end{matrix} \right\} = \int\limits_0^{+\infty} f(z) e^{-paz} a\,dz = aF(pa). \]
Аналогично доказывается вторая формула. $$\blacksquare$$
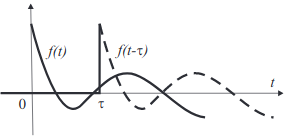
Сдвиг №1
Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо: \[ \chi(t-\tau)f(t-\tau) \supset e^{-p\tau}F(p). \]
Доказательство. Применим преобразование Лапласа к функции $$\chi(t-\tau) f(t-\tau)$$. Сделав замену переменной $$\xi = t-a$$, получим \[ \int\limits_\tau^{+\infty} f(t-\tau) e^{-pt} dt = \int_0^{+\infty} f(\xi) e^{-p(\tau+\xi)} d\xi = e^{-p\tau} F(\xi). \quad \blacksquare \]
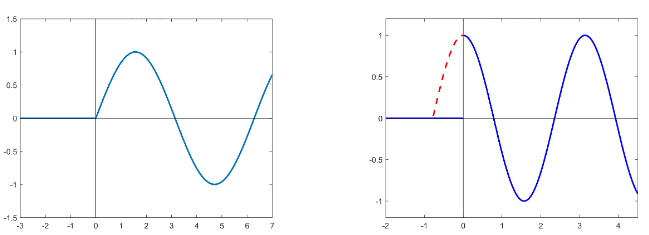
Сдвиг №2
Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо:
\[ \chi(t) f(t+a) \supset e^{pa} \left( F(p) - \int\limits_0^a f(\xi) e^{-p\xi} d\xi \right). \]
Доказательство. Найдём преобразование Лапласа для функции $$\chi(t) f(t+a)$$: \[ \int\limits_0^{+\infty} f(t+a)e^{-pt} dt = \int\limits_0^{+\infty} e^{-p(\xi-a)} d\xi - \int\limits_0^a f(\xi) e^{-p(\xi-a)} d\xi. \quad \blacksquare \]
Заметим, что вычитаемое в этой формуле соответствует утерянной части сигнала.
Дифференцирование оригинала
Если функция $$f(t) \in C'(0, +\infty)$$ и она удовлетворяет достаточным условиям существования прямого преобразования Лапласа, тогда выполнено следующее соотношение: \begin{equation}\label{LT_Deriv} f'(t) \supset pF(p) -f(0+0). \end{equation}
В общем случае: если $$f(t) \in C^{(k)}(0,+\infty)$$ и выполнены достаточные условия существования прямого преобразования, то \begin{equation}\label{LT_Derivk} f^{(k)}(t) \supset p^k F(p) - p^{k-1} f(0+0) - p^{k-2} f'(0+0) - \dots - pf^{(k-2)}(0+0) - f^{(k-1)}(0+0). \end{equation}
Доказательство. Посчитаем преобразование Лапласа от функции $$f'(t)$$. Используя интегрирование по частям, получаем: \[ \int\limits_0^{+\infty} f'(t) e^{-pt} dt = f(t) e^{-pt} \bigg|_0^{+\infty} - \int\limits_0^{+\infty} f(t) (-p) e^{-pt} dt = 0 - f(0+0) + pF(p). \]
Далее найдём изображение второй производной, дважды применив формулу \eqref{LT_Deriv}: \[ f''(t) = \left( f(t) \right)' \supset p\Bigl( pF(p) - f(0+0) \Bigr) - f'(0+0) = p^2 F(p) - pf(0+0) - f'(0+0). \]
Далее, по методу математической индукции, находим: \[ f^{(k)} = \left( f^{(k-1)}(t) \right) \supset p \left( p^{k-1} F(p) -\sum\limits_{l=1}^{k-2} p^{k-2-l} f^{(l)}(0+0) \right) - f^{(k-1)}(0+0). \]
Раскрывая скобки, перейдём к выражению \eqref{LT_Derivk}. $$\blacksquare$$
Дифференцирование изображения
\[ (-t)^k f(t) \supset F^{(k)} (p). \]
Доказательство. Как уже было установлено, изображение $$F(p)$$ является аналитической функцией в полуплоскости $$\mathrm{Re}\,p = \mu > \mu_0$$, а значит её можно дифференцировать по $$p$$ как интеграл, зависящий от параметра. Применим к формуле \eqref{intLapl} $$k$$-кратное дифференцирование: \[ F^{(k)}(p) = \int\limits_0^{+\infty} (-t)^k f(t) e^{-pt} dt. \quad \blacksquare \]
Интегрирование оригинала
\[ \int\limits_0^t f(\tau) d\tau \supset \dfrac{F(p)}{p}. \]
Доказательство. По формуле \eqref{intLapl} получаем, что \[ F(p) = \int\limits_0^{+\infty} e^{-pt} f(t) dt = \int\limits_0^{+\infty} e^{-pt} d\left( \int\limits_0^t f(\tau) d\tau \right). \] Далее применим формулу интегрирования по частям: \[ \int\limits_0^{+\infty} e^{-pt} d\left( \int\limits_0^t f(\tau) d\tau \right) = e^{-pt} \int\limits_0^t f(t) dt \Bigg|_{t=0}^{+\infty} + p\int_0^{+\infty} e^{-pt} dt \int\limits_0^t f(\tau) d\tau = p\int\limits_0^{+\infty} e^{-pt} dt\int\limits_0^t f(\tau) d\tau. \] Так как функция $$f(t)$$ возрастает не быстрее показательной, то мы можем избавиться от первого слагаемого. $$\blacksquare$$
Интегрирование образа
Если интеграл $$\int_p^\infty F(\xi) d\xi$$ сходится по любому пути, целиком лежащему в области $$\mathrm{Re}\,p > \mu_0$$, то он является изображением функции $$f(t)/t$$, т.е. \[ \dfrac{f(t)}{t} \supset \int\limits_p^\infty F(\xi) d\xi. \]
Доказательство. Согласно \eqref{intLapl}: \begin{equation}\label{double_int} \int_p^\infty F(\xi) d\xi = \int_p^\infty d\xi \int\limits_0^{+\infty} f(t) e^{-\xi t} dt. \end{equation}
Предположим, что путь интегрирования $$(p,\infty)$$ целиком лежит в полуплоскости $$\mathrm{Re}\,\xi \ge \mu > \mu_0$$. Дадим оценку внутреннего интеграла: \[ \left| \int\limits_0^{+\infty} f(t) e^{-qt} dt \right| < A \int\limits_0^{+\infty} e^{-(\mu-\mu_0)t} dt = \dfrac{M}{\mu-\mu_0} < \infty. \]
Отсюда по достаточному признаку Вейерштрасса следует равномерная сходимость данного интеграла по параметру $$\xi$$ в области $$\mathrm{Re}\,p > \mu_0$$. Тогда в интеграле \eqref{double_int} можно сменить порядок интегрирования: \[ \int\limits_p^\infty F(\xi) d\xi = \int\limits_0^{+\infty} f(t) dt \int\limits_p^\infty e^{-\xi t} d\xi = \int_0^{+\infty} f(t) \dfrac{e^{-pt}}{t} dt. \quad \blacksquare \]
Свёртка
Напомним, что свёрткой функций $$f(t)$$ и $$g(t)$$ называют функцию вида: \[ f(t)*g(t) \equiv \int\limits_{-\infty}^{+\infty} f(\tau)g(t-\tau) d\tau = \int\limits_{-\infty}^{+\infty} g(\tau) f(t-\tau) d\tau. \] Для функций-оригиналов с учётом того, что $$f(t)\equiv 0$$ и $$g(t)\equiv 0$$ при $$t<0$$ получаем, что \begin{equation}\label{convolution} f(t)*g(t) \equiv \int\limits_0^t f(\tau)g(t-\tau) d\tau. \end{equation}
Свёртка оригиналов соответствует произведению изображений: \[ (f*g)(t) \supset F(p) \cdot G(p). \]
Доказательство. Сначала покажем, что свёртка оригиналов \eqref{convolution} является оригиналом, то есть выполняются достаточные условия существования прямого образования Лапласа. Очевидно, что $$f(t)*g(t) \equiv 0$$ при $$t<0$$. Покажем, что свёртка имеет скорость сходимости не выше экспоненциальной. Так как оригиналы удовлетворяют следующим условиям: \[ |f(t)| < A e^{\mu_0 t}, \quad |g(t)| < B e^{\mu_1 t}, \] то мы имеем следующую оценку абсолютной величины свёртки: \[ |f(t) * g(t)| = \left| \int\limits_0^t f(\tau) g(t-\tau) d\tau \right| < AB \int\limits_0^t e^{\mu_0 \tau} e^{\mu_1 (t-\tau)} d\tau \le AB te^{\mu t}, \] где $$\mu = \max\{ \mu_0, \mu_1 \}$$. Отсюда получаем, что $$|f(t) * g(t)| < C e^{(\mu + \varepsilon) t}$$.
Докажем теперь справедливость формулы для образа свёртки. Согласно \eqref{intLapl}: \[ f(t) * g(t) \supset \int\limits_0^{+\infty} e^{-pt} dt \int_0^t f(\tau) g(t-\tau) d\tau. \]
Поменяем порядок интегрирования в двойном интеграле: \[ \int\limits_0^{+\infty} e^{-pt} dt \int_0^t f(\tau) g(t-\tau) d\tau = \int_0^{+\infty} f(\tau) d\tau \int\limits_\tau^{+\infty}g(t-\tau) e^{-pt} dt = \Bigl\{ t-\tau = \theta \Bigr\} = \int\limits_0^{\infty} f(\tau) d\tau \int\limits_0^{+\infty} g(\theta) e^{-p(\theta + \tau)} d\theta. \quad \blacksquare \]
Периодическая функция
Пусть $$f(t)$$ — периодическая функция с периодом $$T>0$$.
\[ \int\limits_0^{+\infty} f(t) e^{-pt} dt = \sum\limits_{k=1}^{+\infty} \int_{(k-1)T}^{kT} f(t) e^{-pt} dt = \left\{ t = (k-1)T + s \right\} = \sum\limits_{k=1}^{+\infty} \int_0^T f(s) e^{-ps} e^{-p(k-1)T} ds = \left( \sum\limits_{k=1}^{+\infty} e^{-p(k-1)T} \right) \int\limits_0^T f(s) e^{-ps} ds = \dfrac{1}{1-e^{-pT}} \int\limits_0^T f(s) e^{-ps} ds, \] то есть в случае периодической функции достаточно посчитать интеграл Лапласа на одном периоде.
Вычисление обратного преобразования Лапласа
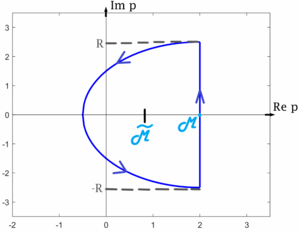
Общий случай
Рассмотрим формулу Меллина \eqref{Mellins_formula}: \[ f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp. \]
В области $$\mu > \mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, \dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} \overset{\Omega_R}{\underset{\R \to +\infty}{\rightrightarrows}} 0$$. Отсюда получаем: \[ f(t)\chi(t) = \frac{1}{2\pi i } \cdot 2\pi i \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) = \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i). \]
Рациональный образ
Напомним, что $$\delta(t) \supset 1$$. Используя элементарные преобразования и свойства преобразования Лапласа можем выписать следующие выражения: \begin{equation}\label{delta} \delta^{(k)}(t) \supset p^k, \quad \delta(t-\alpha) \supset e^{-p\alpha}, \quad \delta^{(k)}(t-\alpha) \supset e^{-p\alpha} p^k. \end{equation}
Пусть функция $$F(p)$$ — рациональная, то есть она имеет вид $$F(p) = \dfrac{Q(p)}{P(p)}$$, где $$Q(p)$$ и $$P(p)$$ — многочлены от переменной $$p$$.
- Пусть $$\deg Q \ge \deg P$$. Тогда можем выполнить деление многочленов и воспользоваться выражениями \eqref{delta}.
- Пусть $$\deg Q \le deg P$$. Тогда эту дробь можно разложить в следующую сумму:
\[ \dfrac{Q(p)}{P(p)} = \dfrac{A_{1m_1}}{(p-\alpha_1)^{m_1}} + \dfrac{A_{1(m_1-1)}}{(p-\alpha_1)^{m_1-1}} + \dots + \dfrac{A_{11}}{p-\alpha_1} + \dfrac{A_{2m_2}}{(p-\alpha_2)^{m_2}} + \dots + \dfrac{A_{21}}{p-\alpha_2} + \dots + \dfrac{B_{11}(p-\eta) + C_{11}}{p^2 + \beta_1 p + \gamma_1} + \dots + \dfrac{B_{1n_1}p + C_{1n_1}}{(p^2 + \beta_1 p + \gamma_1)^{n_1}} + \dots . \]
Теперь, пользуясь линейностью преобразования Лапласа, можем искать прообразы каждого слагаемого по-отдельности. В случае, если в знаменателе стоит выражение степени $$k>1$$, нужно воспользоваться свойством дифференцирования для понижения степени. Иначе, используя элементарные преобразования, получаем, что \[ A_{11} e^{\alpha_1 t} \supset \dfrac{A_{11}}{p-\alpha_1}. \]
Для дробей с квадратным трёхчленом в знаменателе воспользуемся методом выделения полного квадрата: \[ \dfrac{B_{11}p + C_{11}}{p^2 + \beta_1 p + \gamma_1} = \dfrac{B_{11}(p-\eta) + \left( C_{11} + B_{11}\eta \right)}{(p-\eta)^2 + w^2)} = \dfrac{B_{11}(p-\eta)}{(p-\eta)^2 + w^2)} + \dfrac{C_{11} + B_{11}\eta}{(p-\eta)^2 + w^2} \supset B_{11}e^{\eta t} \cos wt + \tilde{C} e^{\eta t} \sin wt . \]