Многозначные отображения и их свойства: различия между версиями
| (не показано 20 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | __TOC__ | ||
Пусть $$(X, \rho_X)$$ и $$(Y, \rho_Y)$$ $$-$$ [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE метрические пространства]. | Пусть $$(X, \rho_X)$$ и $$(Y, \rho_Y)$$ $$-$$ [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE метрические пространства]. | ||
== Определение == | == Определение == | ||
Отображение $$F$$, которое каждому $$x \in X$$ ставит в соответствие непустое замкнутое подмножество $$F(x) \subset Y$$, называется '''многозначным отображением'''. | Отображение $$F$$, которое каждому $$x \in X$$ ставит в соответствие непустое замкнутое подмножество $$F(x) \subset Y$$, называется '''многозначным отображением'''. | ||
| − | == | + | $$\underline{Пример \; 1.}$$ Пусть $$X=Y=\mathbb{R}$$. Ставя в соответствие каждому значению $$x\in X$$ отрезок $$[-|x|,\,|x|]$$, мы получаем многозначное отображение $$F:\mathbb{R} \to \Omega(\mathbb{R}),$$ где $$\Omega(\mathbb{R}) -$$ пространство непустых [https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%B0%D0%BA%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE компактных] подмножеств $$\mathbb{R}$$ с [https://ru.wikipedia.org/wiki/%D0%9C%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0_%D0%A5%D0%B0%D1%83%D1%81%D0%B4%D0%BE%D1%80%D1%84%D0%B0 метрикой Хаусдорфа]. |
| + | |||
| + | == Вспомогательные определения и утверждения == | ||
* Многозначное отображение $$F$$ называется ''секвенциально полунепрерывным сверху в точке $$x_0$$'' $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любой последовательности $$\{y_n\}$$, для которой $$y_n \in F(x_n) \; \forall n$$, имеет место | * Многозначное отображение $$F$$ называется ''секвенциально полунепрерывным сверху в точке $$x_0$$'' $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любой последовательности $$\{y_n\}$$, для которой $$y_n \in F(x_n) \; \forall n$$, имеет место | ||
\[\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty, | \[\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty, | ||
\] | \] | ||
| − | :где $$\text{dist}(y_n, F(x_0)) = \inf\{\ | + | :где $$\text{dist}(y_n, F(x_0)) = \inf\{\rho_{Y}(y_n, y),y \in F(x_0)\}$$. |
Если многозначное отображение секвенциально полунепрерывно сверху в каждой точке, то оно называется ''секвенциально полунепрерывным сверху''. | Если многозначное отображение секвенциально полунепрерывно сверху в каждой точке, то оно называется ''секвенциально полунепрерывным сверху''. | ||
* Многозначное отображение $$F$$ называется ''секвенциально полунепрерывным снизу в точке $$x_0$$'' $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любого $$y_0 \in F(x_0)$$ существует последовательность $$\{y_n\}$$ такая, что $$y_n \in F(x_n) \; \forall n \; \text{и} \; y_n \rightarrow y_0, n \rightarrow \infty$$. | * Многозначное отображение $$F$$ называется ''секвенциально полунепрерывным снизу в точке $$x_0$$'' $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любого $$y_0 \in F(x_0)$$ существует последовательность $$\{y_n\}$$ такая, что $$y_n \in F(x_n) \; \forall n \; \text{и} \; y_n \rightarrow y_0, n \rightarrow \infty$$. | ||
| Строка 14: | Строка 17: | ||
\text{dist}(y_0, F(x)) \rightarrow 0, x \rightarrow x_0, \; \forall y_0 \in F(x_0). | \text{dist}(y_0, F(x)) \rightarrow 0, x \rightarrow x_0, \; \forall y_0 \in F(x_0). | ||
\] | \] | ||
| − | + | ||
| + | $$\underline{Пример \; 2.}$$ Пусть $$X-$$ отрезок $$[0, 2]$$, $$Y-$$ отрезок $$[0, 1]$$ с естественной метрикой. Рассмотрим многозначные отображения $$F_1, F_2$$: | ||
| + | <br> | ||
\[ | \[ | ||
| − | + | \begin{aligned} F_1(x) = \begin{cases} [0, 1]&x \neq 1;\\ \{0\}, &x = 1; \end{cases} \end{aligned} | |
| + | \qquad | ||
| + | \begin{aligned} F_2(x) = \begin{cases} \{0\}, &x \in [0, 1);\\ \{1\}, &x \in (1, 2);\\ [0, 1], &x = 1. \end{cases} \end{aligned} | ||
\] | \] | ||
| + | |||
| + | Многозначное отображение $$F_1$$ секвенциально полунепрерывно снизу, но не является секвенциально полунепрерывным сверху в точке $$x = 1$$, а многозначное отображение $$F_2$$, наоборот, секвенциально полунепрерывно сверху, но не является секвенциально полунепрерывным снизу в точке $$x = 1$$. | ||
| + | |||
| + | * Многозначное отображение $$F$$ называется ''$$h$$-полунепрерывным сверху в точке $$x_0$$'' $$\in X$$, если для произвольного $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что | ||
| + | \[ | ||
| + | F(x) \subset O^Y(F(x_0), \varepsilon) \; \forall x \in O^X(x_0, \delta), | ||
| + | \] | ||
| + | где множество $$O^Y(A, \varepsilon) -$$ это открытая $$\varepsilon$$-окрестность множества $$A \subset Y$$, состоящее из всех таких $$y \in Y$$, что $$\inf\{\rho(y, a), a \in A\} < \varepsilon$$. А множество $$O^X(x_0, \varepsilon) = \{x \in X: \; \rho(x, x_0) < \varepsilon\} -$$ это открытая $$\varepsilon$$-окрестность точки $$x_0$$ в пространстве $$X$$. | ||
| + | |||
Если многозначное отображение $$h$$-полунепрерывно сверху в каждой точке, то оно называется ''$$h$$-полунепрерывным сверху''. | Если многозначное отображение $$h$$-полунепрерывно сверху в каждой точке, то оно называется ''$$h$$-полунепрерывным сверху''. | ||
| − | * Многозначное отображение $$F$$ называется ''$$h$$-полунепрерывным снизу в точке $$x_0$$'' $$\in X$$, если для произвольного $$\ | + | * Многозначное отображение $$F$$ называется ''$$h$$-полунепрерывным снизу в точке $$x_0$$'' $$\in X$$, если для произвольного $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что |
\[ | \[ | ||
| − | O^Y(F(x), \ | + | O^Y(F(x), \varepsilon) \supset F(x_0) \; \forall x \in O^X(x_0, \delta). |
\] | \] | ||
Если многозначное отображение $$h$$-полунепрерывно снизу в каждой точке, то оно называется ''$$h$$-полунепрерывным снизу''. | Если многозначное отображение $$h$$-полунепрерывно снизу в каждой точке, то оно называется ''$$h$$-полунепрерывным снизу''. | ||
| + | |||
| + | $$\underline{Пример \; 3.}$$ Пусть $$F -$$ $$h$$-полунепрерывное снизу многозначное отображение. Возьмем точку $$x_0 \in X$$, и пусть $$A \subset F(x_0) -$$ произвольное замкнутое подмножество (например, $$A = \{y_0\}$$, где $$y_0 -$$ заданная точка из $$F(x_0)$$). Положим | ||
| + | \begin{equation*} | ||
| + | \widetilde{F}(x) = | ||
| + | \begin{cases} | ||
| + | F(x), &x \neq x_0,\\ | ||
| + | A, &x = x_0. | ||
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | :Тогда $$\widetilde{F}$$ также является $$h$$-полунепрерывным снизу многозначным отображением. | ||
| + | [[Файл:1.png|мини|График отображения F для примера 4]] | ||
* Многозначное отображение $$F$$ называется ''непрерывным'', если оно одновременно $$h$$-полунепрерывно и сверху, и снизу. | * Многозначное отображение $$F$$ называется ''непрерывным'', если оно одновременно $$h$$-полунепрерывно и сверху, и снизу. | ||
| + | |||
| + | $$\underline{Пример \; 4.}$$ Пусть $$X-$$ это отрезок $$[0, \pi]$$ и $$Y = \mathbb{R}$$ с естественной метрикой. Тогда многозначное отображение $$F(x) = \Big[0, \sqrt{1-(x-\frac{\pi}{2})^2}\Big]$$ является непрерывным. | ||
| + | |||
Через $$X \times Y$$ обозначим декартово произведение метрических пространств $$(X, \rho_X) \; \text{и} \; (Y, \rho_Y)$$, состоящее из множества упорядоченных пар $$(x, y), \; x\in X, \; y \in Y$$, с метрикой, определяемой соотношением | Через $$X \times Y$$ обозначим декартово произведение метрических пространств $$(X, \rho_X) \; \text{и} \; (Y, \rho_Y)$$, состоящее из множества упорядоченных пар $$(x, y), \; x\in X, \; y \in Y$$, с метрикой, определяемой соотношением | ||
\[ | \[ | ||
| Строка 37: | Строка 67: | ||
\text{gph}F = \{(x, y) \in X \times Y: \; y \in F(x)\}. | \text{gph}F = \{(x, y) \in X \times Y: \; y \in F(x)\}. | ||
\] | \] | ||
| − | Многозначное отображение называется ''замкнутым'', если его график замкнут. | + | Альтернативное обозначение графика отображения $$F$$: $$\; \text{gr}F$$. |
| + | |||
| + | * Многозначное отображение называется ''замкнутым'', если его график замкнут. | ||
| + | |||
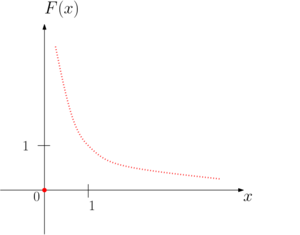
| + | [[Файл:Graph2.png|мини|График отображения F для примера 5]] | ||
| + | $$\underline{Пример \; 5.}$$ Пусть каждое из метрических пространств $$X$$ и $$Y$$ есть множество неотрицательных вещественных чисел с естественной метрикой. Рассмотрим многозначное отображение $$F$$ (на самом деле оно является однозначным, но однозначное отображение является частным случаем многозначного отображения) | ||
| + | \begin{equation*} | ||
| + | F(x) = | ||
| + | \begin{cases} | ||
| + | \{\frac{1}{x}\}, &x > 0,\\ | ||
| + | \{0\}, &x = 0. | ||
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | График этого отображения представляет из себя объединение | ||
| + | графика гиперболы (это замкнутое множество) и точки $$(0, 0)$$; значит, он сам замкнут. | ||
| + | |||
| + | * Многозначное отображение $$F$$ называется ''локально компактным'', если для любой точки $$x \in X$$ существует такая ее окрестность $$O(x)$$, что множество $$F(O(x))$$ предкомпактно (т.е. оно содержится в некотором компакте). | ||
| + | |||
| + | Рассмотрим определения полунепрерывности сверху/снизу в точке, когда $$X \; \text{и} \; Y$$ являются лишь топологическими пространствами. | ||
| + | |||
| + | * Многозначное отображение $$F$$ называется ''полунепрерывным сверху в точке $$x_0 \in X$$'', если для любой окрестности $$O^Y$$ множества $$F(x_0)$$ существует такая окрестность $$O^X$$ точки $$x_0, \; \text{что} \; F(O^X) \subset O^Y$$. | ||
| + | |||
| + | * Многозначное отображение $$F$$ называется ''полунепрерывным снизу в точке $$x_0 \in X$$'', если для любого открытого множества $$O^Y \subset Y$$ такого, что $$O^Y \cap F(x_0) \neq \varnothing$$ существует окрестность $$O^X$$ точки $$x_0$$ такая, что $$F(x) \cap O^Y \neq \varnothing$$ для любого $$x \in O^X$$. | ||
| + | |||
| + | == Свойства == | ||
| + | '''Теорема''' | ||
| + | |||
| + | :''Если многозначное отображение $$F$$ секвенциально полунепрерывно сверху, то оно замкнуто.'' | ||
| + | |||
| + | '''Доказательство.''' Пусть последовательность $$\{(x_n, y_n)\}$$ лежит в графике $$\text{gph}F$$ и сходится к точке $$(x_0, y_0)$$. Достаточно доказать, что $$(x_0, y_0) \in \text{gph}F$$. Действительно, $$y_n \in F(x_n) \; \forall n$$ и $$x_n \rightarrow x_0, y_n \rightarrow y_0, n \rightarrow \infty.$$ Поэтому, в силу секвенциальной полунепрерывности сверху отображения $$F$$ в точке $$x_0$$ имеем $$\text{dist}(y_n, F(x_0)) \rightarrow 0.$$ Отсюда в силу замкнутости множества $$F(x_0)$$ получаем, что $$y_0 \in F(x_0)$$ и, значит, $$(x_0, y_0) \in \text{gph}F$$. $$\blacksquare$$ | ||
| + | |||
| + | '''Теорема''' | ||
| + | |||
| + | :''Пусть пространство $$Y$$ [https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BC%D0%BF%D0%B0%D0%BA%D1%82%D0%BD%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE компактно]. Тогда многозначное отображение секвенциально полунепрерывно сверху тогда и только тогда, когда оно замкнуто.'' | ||
| + | |||
| + | '''Доказательство.''' В силу предыдущей теоремы достаточно доказать, что если многозначное отображение $$F$$ замкнуто, то оно секвенциально полунепрерывно сверху в каждой точке $$x_0 \in X$$. Пусть последовательность $$\{x_n\}$$ сходится к точке $$x_0$$ и для последовательности $$\{y_n\}$$ имеет место $$y_n \in F(x_n) \; \forall n$$. Докажем, что тогда $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n\rightarrow \infty$$. | ||
| + | |||
| + | Будем действовать от противного. Пусть существует такое $$\varepsilon > 0$$, что после перехода от последовательности $$\{y_n\}$$ к ее подпоследовательности выполняется $$\text{dist}(y_n, F(x_0)) \geqslant \varepsilon \; \forall n.$$ В силу компактности пространства $$Y$$, переходя еще раз к подпоследовательности, будем считать, что $$y_n \rightarrow y_0$$ для некоторого $$y_0 \in Y$$. Тогда $$(x_n, y_n) \rightarrow (x_0, y_0) \; \text{и} \; (x_n, y_n) \in \text{gph}F \; \forall n.$$ Поэтому $$(x_0, y_0) \in \text{gph}F$$ в силу замкнутости множества $$\text{gph}F$$ и, значит, | ||
| + | \[ | ||
| + | y_0 \in F(x_0) \Rightarrow \text{dist}(y_n, F(x_0)) \leqslant \rho_Y(y_n, y_0), | ||
| + | \] | ||
| + | откуда $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty.$$ Полученное противоречие с установленным выше неравенством завершает доказательство. $$\blacksquare$$ | ||
| + | |||
| + | '''Теорема''' | ||
| + | |||
| + | :''Пусть многозначное отображение $$F$$ замкнуто и локально компактно. Тогда оно секвенциально полунепрерывно сверху.'' | ||
| + | |||
| + | '''Доказательство''' этого утверждения повторяет доказательство теоремы выше. | ||
| + | |||
| + | Пусть заданы многозначные отображения $$F_j, j \in J$$, где $$J$$ некоторое множество индексов. Определим новые многозначные отображения $$-$$ объединение и пересечение исходных отображений $$-$$ соотношениями | ||
| + | \[ | ||
| + | \Big(\bigcup_{j \in J}F_{j}\Big)(x) = \bigcup_{j \in J}F_{j}(x), \; \Big(\bigcap_{j \in J}F_{j}\Big)(x) = \bigcap_{j \in J}F_{j}(x) | ||
| + | \] | ||
| + | При этом предполагается, что в формуле для объединения множество индексов $$J$$ конечно и второе многозначное отображение корректно определено, т.е. что | ||
| + | \[ | ||
| + | \bigcap_{j \in J}F_{j}(x) \neq \varnothing \; \forall x. | ||
| + | \] | ||
| + | |||
| + | '''Теорема''' | ||
| + | |||
| + | :''Пусть заданы два многозначных отображения: $$F_1 \; \text{и} \; F_2$$, причем $$F_1$$ замкнуто, а $$F_2$$ полунепрерывно сверху и компактнозначно. Тогда если их пересечение $$F = F_1 \cap F_2$$ корректно определено, то оно полунепрерывно сверху.'' | ||
| + | |||
| + | '''Доказательство.''' Возьмем произвольную точку $$x_0 \in X$$ и докажем, что многозначное отображение $$F$$ в ней секвенциально полунепрерывно сверху. Пусть последовательность $$\{x_n\}$$ сходится к точке $$x_0$$ и $$y_n \in F(x_n) \; \forall n.$$ Докажем, что $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty$$. Предположим противное. Тогда существует такое $$\varepsilon > 0$$, что после перехода к подпоследовательности, имеем $$\text{dist}(y_n, F(x_0)) \geqslant \varepsilon \; \forall n.$$ | ||
| + | |||
| + | Но $$y_n \in F_2(x_n) \; \forall n \; \text{и, значит,} \; \text{dist}(y_n, F_2(x_0)) \rightarrow 0$$ в силу секвенциальной полунепрерывности сверху $$F_2$$. Докажем существование такого $$y_0 \in F_2(x_0)$$, что после перехода к подпоследовательности имеет место $$y_n \rightarrow y_0$$. Действительно, в силу доказанного, для каждого $$n$$ существует такое $$\widetilde{y_n} \in F_2(x_0)$$, что $$\rho_Y(\widetilde{y_n}, y_n) \rightarrow 0.$$ В силу компактности множества $$F_2(x_0)$$, переходя к подпоследовательности, получаем, что $$\widetilde{y_n} \rightarrow y_0$$ для некоторого $$y_0 \in F_2(x_0)$$. Отсюда с помощью неравенства треугольника получаем $$y_n \rightarrow y_0$$, что доказывает треубемое. | ||
| + | |||
| + | Кроме того, $$y_n \in F_1(x_n) \; \forall n$$, откуда в силу замкнутости $$F_1$$ имеем $$y_0 \in F_1(x_0)$$. Таким образом, доказано, что $$y_0 \in F(x_0)$$ и, значит, для указанной подпоследовательности имеет место $$\text{dist}(y_n, F(x_0)) \rightarrow 0$$, что противоречит выбору $$\varepsilon > 0$$. $$\blacksquare$$ | ||
| + | |||
| + | Многозначные отображения находят приложения в различных областях математики: негладком и выпуклом анализе, теории дифференциальных уравнений, теории управления, теории игр и математической экономике. | ||
| + | |||
| + | == Список литературы == | ||
| + | ''Арутюнов А. В.'' Лекции по выпуклому и многозначному анализу. — М.: ФИЗМАТЛИТ, 2014 | ||
Текущая версия на 13:56, 4 ноября 2022
Пусть $$(X, \rho_X)$$ и $$(Y, \rho_Y)$$ $$-$$ метрические пространства.
Определение
Отображение $$F$$, которое каждому $$x \in X$$ ставит в соответствие непустое замкнутое подмножество $$F(x) \subset Y$$, называется многозначным отображением.
$$\underline{Пример \; 1.}$$ Пусть $$X=Y=\mathbb{R}$$. Ставя в соответствие каждому значению $$x\in X$$ отрезок $$[-|x|,\,|x|]$$, мы получаем многозначное отображение $$F:\mathbb{R} \to \Omega(\mathbb{R}),$$ где $$\Omega(\mathbb{R}) -$$ пространство непустых компактных подмножеств $$\mathbb{R}$$ с метрикой Хаусдорфа.
Вспомогательные определения и утверждения
- Многозначное отображение $$F$$ называется секвенциально полунепрерывным сверху в точке $$x_0$$ $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любой последовательности $$\{y_n\}$$, для которой $$y_n \in F(x_n) \; \forall n$$, имеет место
\[\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty, \]
- где $$\text{dist}(y_n, F(x_0)) = \inf\{\rho_{Y}(y_n, y),y \in F(x_0)\}$$.
Если многозначное отображение секвенциально полунепрерывно сверху в каждой точке, то оно называется секвенциально полунепрерывным сверху.
- Многозначное отображение $$F$$ называется секвенциально полунепрерывным снизу в точке $$x_0$$ $$\in X$$, если для любой последовательности $$\{x_n\}$$, сходящейся к точке $$x_0$$, и любого $$y_0 \in F(x_0)$$ существует последовательность $$\{y_n\}$$ такая, что $$y_n \in F(x_n) \; \forall n \; \text{и} \; y_n \rightarrow y_0, n \rightarrow \infty$$.
Если многозначное отображение секвенциально полунепрерывно снизу в каждой точке, то оно называется секвенциально полунепрерывным снизу, что равносильно тому, что \[ \text{dist}(y_0, F(x)) \rightarrow 0, x \rightarrow x_0, \; \forall y_0 \in F(x_0). \]
$$\underline{Пример \; 2.}$$ Пусть $$X-$$ отрезок $$[0, 2]$$, $$Y-$$ отрезок $$[0, 1]$$ с естественной метрикой. Рассмотрим многозначные отображения $$F_1, F_2$$:
\[
\begin{aligned} F_1(x) = \begin{cases} [0, 1]&x \neq 1;\\ \{0\}, &x = 1; \end{cases} \end{aligned}
\qquad
\begin{aligned} F_2(x) = \begin{cases} \{0\}, &x \in [0, 1);\\ \{1\}, &x \in (1, 2);\\ [0, 1], &x = 1. \end{cases} \end{aligned}
\]
Многозначное отображение $$F_1$$ секвенциально полунепрерывно снизу, но не является секвенциально полунепрерывным сверху в точке $$x = 1$$, а многозначное отображение $$F_2$$, наоборот, секвенциально полунепрерывно сверху, но не является секвенциально полунепрерывным снизу в точке $$x = 1$$.
- Многозначное отображение $$F$$ называется $$h$$-полунепрерывным сверху в точке $$x_0$$ $$\in X$$, если для произвольного $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что
\[ F(x) \subset O^Y(F(x_0), \varepsilon) \; \forall x \in O^X(x_0, \delta), \] где множество $$O^Y(A, \varepsilon) -$$ это открытая $$\varepsilon$$-окрестность множества $$A \subset Y$$, состоящее из всех таких $$y \in Y$$, что $$\inf\{\rho(y, a), a \in A\} < \varepsilon$$. А множество $$O^X(x_0, \varepsilon) = \{x \in X: \; \rho(x, x_0) < \varepsilon\} -$$ это открытая $$\varepsilon$$-окрестность точки $$x_0$$ в пространстве $$X$$.
Если многозначное отображение $$h$$-полунепрерывно сверху в каждой точке, то оно называется $$h$$-полунепрерывным сверху.
- Многозначное отображение $$F$$ называется $$h$$-полунепрерывным снизу в точке $$x_0$$ $$\in X$$, если для произвольного $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что
\[ O^Y(F(x), \varepsilon) \supset F(x_0) \; \forall x \in O^X(x_0, \delta). \] Если многозначное отображение $$h$$-полунепрерывно снизу в каждой точке, то оно называется $$h$$-полунепрерывным снизу.
$$\underline{Пример \; 3.}$$ Пусть $$F -$$ $$h$$-полунепрерывное снизу многозначное отображение. Возьмем точку $$x_0 \in X$$, и пусть $$A \subset F(x_0) -$$ произвольное замкнутое подмножество (например, $$A = \{y_0\}$$, где $$y_0 -$$ заданная точка из $$F(x_0)$$). Положим \begin{equation*} \widetilde{F}(x) = \begin{cases} F(x), &x \neq x_0,\\ A, &x = x_0. \end{cases} \end{equation*}
- Тогда $$\widetilde{F}$$ также является $$h$$-полунепрерывным снизу многозначным отображением.
- Многозначное отображение $$F$$ называется непрерывным, если оно одновременно $$h$$-полунепрерывно и сверху, и снизу.
$$\underline{Пример \; 4.}$$ Пусть $$X-$$ это отрезок $$[0, \pi]$$ и $$Y = \mathbb{R}$$ с естественной метрикой. Тогда многозначное отображение $$F(x) = \Big[0, \sqrt{1-(x-\frac{\pi}{2})^2}\Big]$$ является непрерывным.
Через $$X \times Y$$ обозначим декартово произведение метрических пространств $$(X, \rho_X) \; \text{и} \; (Y, \rho_Y)$$, состоящее из множества упорядоченных пар $$(x, y), \; x\in X, \; y \in Y$$, с метрикой, определяемой соотношением \[ \rho((x_1, y_1), (x_2, y_2)) = \rho_X(x_1, x_2) + \rho_Y(y_1, y_2). \] Для сходимости в метрическом пространстве $$X \times Y$$ справедливо следующее: \[ (x_n, y_n) \rightarrow (x_0, y_0) \Leftrightarrow x_n \rightarrow x_0, \; y_n \rightarrow y_0, \; n \rightarrow \infty. \]
- Графиком многозначного отображения $$F$$ называется множество
\[ \text{gph}F = \{(x, y) \in X \times Y: \; y \in F(x)\}. \] Альтернативное обозначение графика отображения $$F$$: $$\; \text{gr}F$$.
- Многозначное отображение называется замкнутым, если его график замкнут.
$$\underline{Пример \; 5.}$$ Пусть каждое из метрических пространств $$X$$ и $$Y$$ есть множество неотрицательных вещественных чисел с естественной метрикой. Рассмотрим многозначное отображение $$F$$ (на самом деле оно является однозначным, но однозначное отображение является частным случаем многозначного отображения) \begin{equation*} F(x) = \begin{cases} \{\frac{1}{x}\}, &x > 0,\\ \{0\}, &x = 0. \end{cases} \end{equation*} График этого отображения представляет из себя объединение графика гиперболы (это замкнутое множество) и точки $$(0, 0)$$; значит, он сам замкнут.
- Многозначное отображение $$F$$ называется локально компактным, если для любой точки $$x \in X$$ существует такая ее окрестность $$O(x)$$, что множество $$F(O(x))$$ предкомпактно (т.е. оно содержится в некотором компакте).
Рассмотрим определения полунепрерывности сверху/снизу в точке, когда $$X \; \text{и} \; Y$$ являются лишь топологическими пространствами.
- Многозначное отображение $$F$$ называется полунепрерывным сверху в точке $$x_0 \in X$$, если для любой окрестности $$O^Y$$ множества $$F(x_0)$$ существует такая окрестность $$O^X$$ точки $$x_0, \; \text{что} \; F(O^X) \subset O^Y$$.
- Многозначное отображение $$F$$ называется полунепрерывным снизу в точке $$x_0 \in X$$, если для любого открытого множества $$O^Y \subset Y$$ такого, что $$O^Y \cap F(x_0) \neq \varnothing$$ существует окрестность $$O^X$$ точки $$x_0$$ такая, что $$F(x) \cap O^Y \neq \varnothing$$ для любого $$x \in O^X$$.
Свойства
Теорема
- Если многозначное отображение $$F$$ секвенциально полунепрерывно сверху, то оно замкнуто.
Доказательство. Пусть последовательность $$\{(x_n, y_n)\}$$ лежит в графике $$\text{gph}F$$ и сходится к точке $$(x_0, y_0)$$. Достаточно доказать, что $$(x_0, y_0) \in \text{gph}F$$. Действительно, $$y_n \in F(x_n) \; \forall n$$ и $$x_n \rightarrow x_0, y_n \rightarrow y_0, n \rightarrow \infty.$$ Поэтому, в силу секвенциальной полунепрерывности сверху отображения $$F$$ в точке $$x_0$$ имеем $$\text{dist}(y_n, F(x_0)) \rightarrow 0.$$ Отсюда в силу замкнутости множества $$F(x_0)$$ получаем, что $$y_0 \in F(x_0)$$ и, значит, $$(x_0, y_0) \in \text{gph}F$$. $$\blacksquare$$
Теорема
- Пусть пространство $$Y$$ компактно. Тогда многозначное отображение секвенциально полунепрерывно сверху тогда и только тогда, когда оно замкнуто.
Доказательство. В силу предыдущей теоремы достаточно доказать, что если многозначное отображение $$F$$ замкнуто, то оно секвенциально полунепрерывно сверху в каждой точке $$x_0 \in X$$. Пусть последовательность $$\{x_n\}$$ сходится к точке $$x_0$$ и для последовательности $$\{y_n\}$$ имеет место $$y_n \in F(x_n) \; \forall n$$. Докажем, что тогда $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n\rightarrow \infty$$.
Будем действовать от противного. Пусть существует такое $$\varepsilon > 0$$, что после перехода от последовательности $$\{y_n\}$$ к ее подпоследовательности выполняется $$\text{dist}(y_n, F(x_0)) \geqslant \varepsilon \; \forall n.$$ В силу компактности пространства $$Y$$, переходя еще раз к подпоследовательности, будем считать, что $$y_n \rightarrow y_0$$ для некоторого $$y_0 \in Y$$. Тогда $$(x_n, y_n) \rightarrow (x_0, y_0) \; \text{и} \; (x_n, y_n) \in \text{gph}F \; \forall n.$$ Поэтому $$(x_0, y_0) \in \text{gph}F$$ в силу замкнутости множества $$\text{gph}F$$ и, значит, \[ y_0 \in F(x_0) \Rightarrow \text{dist}(y_n, F(x_0)) \leqslant \rho_Y(y_n, y_0), \] откуда $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty.$$ Полученное противоречие с установленным выше неравенством завершает доказательство. $$\blacksquare$$
Теорема
- Пусть многозначное отображение $$F$$ замкнуто и локально компактно. Тогда оно секвенциально полунепрерывно сверху.
Доказательство этого утверждения повторяет доказательство теоремы выше.
Пусть заданы многозначные отображения $$F_j, j \in J$$, где $$J$$ некоторое множество индексов. Определим новые многозначные отображения $$-$$ объединение и пересечение исходных отображений $$-$$ соотношениями \[ \Big(\bigcup_{j \in J}F_{j}\Big)(x) = \bigcup_{j \in J}F_{j}(x), \; \Big(\bigcap_{j \in J}F_{j}\Big)(x) = \bigcap_{j \in J}F_{j}(x) \] При этом предполагается, что в формуле для объединения множество индексов $$J$$ конечно и второе многозначное отображение корректно определено, т.е. что \[ \bigcap_{j \in J}F_{j}(x) \neq \varnothing \; \forall x. \]
Теорема
- Пусть заданы два многозначных отображения: $$F_1 \; \text{и} \; F_2$$, причем $$F_1$$ замкнуто, а $$F_2$$ полунепрерывно сверху и компактнозначно. Тогда если их пересечение $$F = F_1 \cap F_2$$ корректно определено, то оно полунепрерывно сверху.
Доказательство. Возьмем произвольную точку $$x_0 \in X$$ и докажем, что многозначное отображение $$F$$ в ней секвенциально полунепрерывно сверху. Пусть последовательность $$\{x_n\}$$ сходится к точке $$x_0$$ и $$y_n \in F(x_n) \; \forall n.$$ Докажем, что $$\text{dist}(y_n, F(x_0)) \rightarrow 0, n \rightarrow \infty$$. Предположим противное. Тогда существует такое $$\varepsilon > 0$$, что после перехода к подпоследовательности, имеем $$\text{dist}(y_n, F(x_0)) \geqslant \varepsilon \; \forall n.$$
Но $$y_n \in F_2(x_n) \; \forall n \; \text{и, значит,} \; \text{dist}(y_n, F_2(x_0)) \rightarrow 0$$ в силу секвенциальной полунепрерывности сверху $$F_2$$. Докажем существование такого $$y_0 \in F_2(x_0)$$, что после перехода к подпоследовательности имеет место $$y_n \rightarrow y_0$$. Действительно, в силу доказанного, для каждого $$n$$ существует такое $$\widetilde{y_n} \in F_2(x_0)$$, что $$\rho_Y(\widetilde{y_n}, y_n) \rightarrow 0.$$ В силу компактности множества $$F_2(x_0)$$, переходя к подпоследовательности, получаем, что $$\widetilde{y_n} \rightarrow y_0$$ для некоторого $$y_0 \in F_2(x_0)$$. Отсюда с помощью неравенства треугольника получаем $$y_n \rightarrow y_0$$, что доказывает треубемое.
Кроме того, $$y_n \in F_1(x_n) \; \forall n$$, откуда в силу замкнутости $$F_1$$ имеем $$y_0 \in F_1(x_0)$$. Таким образом, доказано, что $$y_0 \in F(x_0)$$ и, значит, для указанной подпоследовательности имеет место $$\text{dist}(y_n, F(x_0)) \rightarrow 0$$, что противоречит выбору $$\varepsilon > 0$$. $$\blacksquare$$
Многозначные отображения находят приложения в различных областях математики: негладком и выпуклом анализе, теории дифференциальных уравнений, теории управления, теории игр и математической экономике.
Список литературы
Арутюнов А. В. Лекции по выпуклому и многозначному анализу. — М.: ФИЗМАТЛИТ, 2014