Достаточные условия существования оптимального управления: различия между версиями
Liza22 (обсуждение | вклад) |
Liza22 (обсуждение | вклад) |
||
| (не показано 89 промежуточных версий 2 участников) | |||
| Строка 1: | Строка 1: | ||
| + | == Аннотация == | ||
| + | В этой статье будет рассмотрена теорема существования оптимального управления для нелинейной системы в $$\mathbb{R}^n$$: | ||
| + | \begin{gather*} | ||
| + | \dot x = f(t, x(t), u(t)) | ||
| + | \end{gather*} | ||
| + | |||
| + | Приведём контрпримеры, демонстрирующие невозможность отыскать оптимальное управление при помощи [https://sawiki.cs.msu.ru/index.php/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BC%D0%B0%D0%BA%D1%81%D0%B8%D0%BC%D1%83%D0%BC%D0%B0_%D0%9B.%D0%A1._%D0%9F%D0%BE%D0%BD%D1%82%D1%80%D1%8F%D0%B3%D0%B8%D0%BD%D0%B0_%D0%B4%D0%BB%D1%8F_%D0%BE%D0%B1%D1%89%D0%B5%D0%B9_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F ПМП]. | ||
| + | |||
| + | == Случаи, когда решения не существует== | ||
| + | === Пример 1 === | ||
| + | Множество допустимых пар $$\{x(\cdot),\ u(\cdot)\}$$ пусто: | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = 0, \\ | ||
| + | x(0) = 0,\\ | ||
| + | x(1) = 1. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
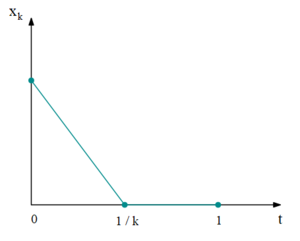
| + | === Пример 2 === | ||
| + | Ограничивающее множество $$\mathcal{P} \notin \mathrm{conv}~\R$$ | ||
| + | [[Файл:Elis1.png|мини|справа]] | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = u, & u \in \R, \\ | ||
| + | x(0) = 1,\\ | ||
| + | x(1) = 0. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | J = \int_0^1 x^2(t) dt \to \inf. | ||
| + | \end{gather*} | ||
| + | |||
| + | Перейдём к расширенной системе: | ||
| + | |||
| + | \begin{equation*} | ||
| + | \begin{cases} | ||
| + | \dot{x_0} = x_1^2, \\ | ||
| + | \dot{x_1} = u. | ||
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | |||
| + | Тогда функция Гамильтона-Понтрягина примет вид: | ||
| + | \begin{gather*} | ||
| + | \mathcal{H} = \psi_0 x_1^2 + \psi_1 u, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{\psi}_0 = 0, \\ | ||
| + | \dot{\psi}_1 = -2 \psi_0 x_1. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | В этом случае $$u = \pm \infty$$. Рассмотрим управления $$u_k$$: | ||
| + | \begin{gather*} | ||
| + | u_k(t) = | ||
| + | \begin{cases} | ||
| + | -k, &\; t \in \left[0, \frac{1}{k}\right],\\ | ||
| + | 0, &\; \text{иначе}. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | x_k(t) = | ||
| + | \begin{cases} | ||
| + | 1-kt,\; t \in \left[0, \frac{1}{k}\right],\\ | ||
| + | 0,\; \text{иначе}. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | Тогда $$\mathrm{inf}J(\cdot) = 0$$, т.к. $$J(\cdot) \geqslant 0.$$ | ||
| + | |||
| + | \begin{gather*} | ||
| + | J\left(u_k(\cdot)\right) = \int\limits_0^{\frac{1}{k}}(1 - kt)^2 dt = \frac{1}{3k} \underset{k \rightarrow +\infty}{\rightarrow} 0. | ||
| + | \end{gather*} | ||
| + | |||
| + | Но $$\mathrm{inf}J(\cdot)$$ не достигается в силу непрерывности $$x(\cdot)$$. | ||
| + | |||
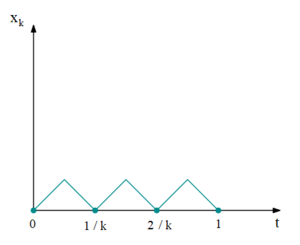
| + | === Пример 3 === | ||
| + | Множество обобщенных скоростей (векторграмма) $$\mathcal{F}(t,\ \overline{x}) \notin \mathrm{conv}~\R^{n+1}$$ | ||
| + | [[Файл:2.png|мини]] | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = u, \; |u| \leqslant 1, \\ | ||
| + | x(0) = x(1) = 0. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | J = \int_0^1 [x^2(t) + (1 - u^2(t))^2] dt \rightarrow \underset{u(\cdot)}{\mathrm{inf}}. | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | \mathcal{H} = \psi_0 (u_1^2 + (1 - u^2)^2) + \psi_1 u, \\ | ||
| + | \begin{cases} | ||
| + | \dot{\psi}_0 = 0, \\ | ||
| + | \dot{\psi}_1 = -2 \psi_0 x_1. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | u_k(t) = | ||
| + | \begin{cases} | ||
| + | 1, \; t \in \left[\frac{2j}{2k}, \frac{2j + 1}{2k}\right],\\ | ||
| + | -1, \; t \in \left[\frac{2j + 1}{2k}, \frac{2j + 2}{2k}\right]. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | x_k(t) = | ||
| + | \begin{cases} | ||
| + | t - \frac{2j}{2k}, \; t \in \left[\frac{2j}{2k}, \frac{2j + 1}{2k}\right],\\ | ||
| + | -t + \frac{2j + 2}{2k}, \; t \in \left[\frac{2j + 1}{2k}, \frac{2j + 2}{2k}\right]. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | J\left(u_k(\cdot)\right) = k \int\limits_0^{\frac{1}{k}} x_k^2(t) dt = 2k \int\limits_0^{\frac{1}{2k}} t^2 dt = \frac{1}{3(2k)^2} \underset{k \rightarrow +\infty}{\rightarrow} 0. | ||
| + | \end{gather*} | ||
| + | |||
| + | Таким образом, $$\mathrm{inf}J(\cdot)$$ не достигается даже при ограничении $$|u| \leqslant 1$$. | ||
| + | |||
| + | ''Замечание:'' В отличие от '''Примера 2''' [https://sawiki.cs.msu.ru/index.php/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BC%D0%B0%D0%BA%D1%81%D0%B8%D0%BC%D1%83%D0%BC%D0%B0_%D0%9B.%D0%A1._%D0%9F%D0%BE%D0%BD%D1%82%D1%80%D1%8F%D0%B3%D0%B8%D0%BD%D0%B0_%D0%B4%D0%BB%D1%8F_%D0%BE%D0%B1%D1%89%D0%B5%D0%B9_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F ПМП] даёт результат, но неправильный. | ||
| + | |||
| + | === Пример 4 === | ||
| + | $$E = \{e = (t_0,\ x^0, t_1, x^1): \varphi(e) = 0\}$$ $$-$$ компакт, $$\overline{\varphi} = (\varphi_0,\ \varphi)$$ | ||
| + | |||
| + | $$\overline{\varphi} \notin C(E)$$ | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = u, \; |u| \leqslant 1,\\ | ||
| + | x(0) = 0,\\ | ||
| + | t_1 x(t_1) = 1. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | J = x(t_1) \rightarrow \mathrm{inf}. | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | \mathcal{H} = \psi_1 u, | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | u^* = | ||
| + | \begin{cases} | ||
| + | 1, \; \psi_1 > 0, \\ | ||
| + | [-1, 1],\; \psi_1 = 0, \\ | ||
| + | -1, \;\psi_1 < 0. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | Отсюда: | ||
| + | \begin{gather*} | ||
| + | \begin{matrix} | ||
| + | \dot{\psi_1} = 0, \\ | ||
| + | \psi_1[0] = - \lambda_3 \; \mathcal{H}\vert_{t = t_0} = \lambda_2, \\ | ||
| + | \psi_1[t_1] = \lambda_0 + \lambda_1 t_1 \; \mathcal{H} \vert_{t = t_1} = -\lambda_1 x(t_1). | ||
| + | \end{matrix} | ||
| + | \end{gather*} | ||
| + | |||
| + | Фиксируем $$\tau > 0$$: | ||
| + | \begin{gather*} | ||
| + | u(t) = | ||
| + | \begin{cases} | ||
| + | 0, \; t \in [0, \tau], \\ | ||
| + | 1, \; t > \tau. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | x(t) = | ||
| + | \begin{cases} | ||
| + | 0, \; t \in [0, \tau], \\ | ||
| + | t - \tau, \; t > \tau. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | |||
| + | \begin{gather*} | ||
| + | x(t_1) t_1 = 1 \Rightarrow t_1^2 - \tau t_1 - 1 = 0,\\ | ||
| + | t_1 = \frac{\tau + \sqrt{\tau^2 + 4}}{2}. | ||
| + | \end{gather*} | ||
| + | |||
| + | При $$\tau \rightarrow +\infty$$: $$t_1 \rightarrow +\infty$$ и $$x(t_1) = \frac{1}{t_1} \rightarrow 0$$. Следовательно, $$\mathrm{inf}J(\cdot) = 0$$ не достигается. | ||
| + | |||
== Теорема о существовании оптимального управления == | == Теорема о существовании оптимального управления == | ||
| − | Пусть $$\dot x = f(t, x(t), u(t)),\ u(t) \in \mathcal{P}$$, где $$f$$ удовлетворяет описанию, обозначенному в [https://sawiki.cs.msu.ru/index.php/%D0%A0%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F_%D0%9E%D0%94%D0%A3_%D0%B2_%D1%81%D0%BC%D1%8B%D1%81%D0%BB%D0%B5_%D0%9A%D0%B0%D1%80%D0%B0%D1%82%D0%B5%D0%BE%D0%B4%D0%BE%D1%80%D0%B8 итоговых условиях на функцию | + | Пусть $$\dot x = f(t, x(t), u(t)),\ u(t) \in \mathcal{P}$$, где $$f$$ удовлетворяет описанию, обозначенному в [https://sawiki.cs.msu.ru/index.php/%D0%A0%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D1%8F_%D0%9E%D0%94%D0%A3_%D0%B2_%D1%81%D0%BC%D1%8B%D1%81%D0%BB%D0%B5_%D0%9A%D0%B0%D1%80%D0%B0%D1%82%D0%B5%D0%BE%D0%B4%D0%BE%D1%80%D0%B8 итоговых условиях на функцию]: |
\begin{gather*} | \begin{gather*} | ||
| − | \varphi_0(e) \rightarrow \infty\\ | + | \varphi_0(e) \rightarrow \infty,\\ |
| − | \varphi_1(e) = \varphi_2(e) = \ldots = \varphi_k(e) = 0 | + | \varphi_1(e) = \varphi_2(e) = \ldots = \varphi_k(e) = 0. |
\end{gather*} | \end{gather*} | ||
Пусть также: | Пусть также: | ||
| − | # Множество допустимых пар $$\{x(\cdot),\ u(\cdot)\}$$ не пусто, то есть $$S^1 = \{(t_0,\ t_1,\ x^0,\ u(\cdot)) \in S | \varphi(e) = 0,\ e = e(t_0,\ t_1,\ x^0,\ u(\cdot))\} \neq \emptyset$$ | + | # Множество допустимых пар $$\{x(\cdot),\ u(\cdot)\}$$ не пусто, то есть $$S^1 = \{(t_0,\ t_1,\ x^0,\ u(\cdot)) \in S | \varphi(e) = 0,\ e = e(t_0,\ t_1,\ x^0,\ u(\cdot))\} \neq \emptyset$$. [[#Пример 1|Пример 1.]] |
| − | # $$\mathcal{P} \in \mathbb{R}^m$$ | + | # $$\mathcal{P} \in \mathbb{R}^m$$. [[#Пример 2|Пример 2.]] |
| − | # $$\mathcal{F}(t,\ x) = \bigcup\limits_{u \in \mathcal{P}}\{f(t,\ x,\ u)\} \in \mathrm{conv}~\R^n$$, $$F(t,\ x) -$$ множество возможных скоростей (векторграмма) | + | # $$\mathcal{F}(t,\ \overline{x}) = \bigcup\limits_{u \in \mathcal{P}}\{\overline{f}(t,\ \overline{x},\ u)\} \in \mathrm{conv}~\R^{n+1}$$, $$\mathcal{F}(t,\ \overline{x})$$ $$-$$ множество возможных скоростей (векторграмма). [[#Пример 3|Пример 3.]] |
| − | # $$E = \{e = (t_0,\ x^0, t_1, x^1) \in \mathbb{R}^{2n+2}: \varphi(e) = 0\} -$$ компакт, $$\overline{\varphi} \in C(E)$$ | + | # $$E = \{e = (t_0,\ x^0, t_1, x^1) \in \mathbb{R}^{2n+2}: \varphi(e) = 0\}$$ $$-$$ компакт, $$\overline{\varphi} = (\varphi_0,\ \varphi) \in C(E)$$. [[#Пример 4|Пример 4.]] |
| − | Тогда решение задачи оптимального управления существует ($$\exists u^* -$$ измеримое). | + | Тогда решение задачи оптимального управления существует ($$\exists u^*$$ $$-$$ измеримое). |
| − | ''Замечание:'' Если $$f(t,\ x,\ u) = f^0(t,\ x) + g(t,\ x)\cdot u$$, то условие $$3$$ можно заменить на $$\mathcal{P} \in \mathrm{conv}~\R^n$$ | + | ''Замечание:'' Если $$f(t,\ x,\ u) = f^0(t,\ x) + g(t,\ x)\cdot u$$, то условие $$3$$ можно заменить на $$\mathcal{P} \in \mathrm{conv}~\R^{n+1}$$. |
| − | + | === Доказательство === | |
| − | Пусть $$\varphi_* = \mathrm{inf}\{\varphi_0(e): e = e(s), s \in S^1\}$$, $$\varphi_* > -\infty$$, т.к. $$\overline{\varphi} \in C(E)$$, $$E - $$ компакт. По определению инфимума: | + | Пусть $$\varphi_* = \mathrm{inf}\{\varphi_0(e): e = e(s), s \in S^1\}$$, $$\varphi_* > -\infty$$, т.к. $$\overline{\varphi} \in C(E)$$, $$E$$ $$-$$ компакт. По определению инфимума: |
\begin{gather*} | \begin{gather*} | ||
| − | \forall \varepsilon = \frac{1}{k} \;\; \exists (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}): \;\; \varphi_* \leqslant \varphi_0(e^{(k)}) \leqslant \varphi_* + \frac{1}{k},\ e^{(k)} = (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}) | + | \forall \varepsilon = \frac{1}{k} \;\; \exists (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}): \;\; \varphi_* \leqslant \varphi_0(e^{(k)}) \leqslant \varphi_* + \frac{1}{k},\ e^{(k)} = (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}). |
\end{gather*} | \end{gather*} | ||
''План доказательства:'' | ''План доказательства:'' | ||
| − | * Доказать, что $$x^{(k)}(\cdot) \ | + | * Доказать, что $$x^{(k)}(\cdot) \underset{k \rightarrow \infty}{\rightarrow} x^*(\cdot)$$ в пространстве $$C$$. |
* Доказать, что $$x^*(\cdot)$$ порождается некоторым управлением $$u^*(\cdot)$$. | * Доказать, что $$x^*(\cdot)$$ порождается некоторым управлением $$u^*(\cdot)$$. | ||
| − | Без ограничения общности, положим $$t_0^{(k)}(\cdot) \rightarrow t_0^*$$, $$t_1^{(k)}(\cdot) \rightarrow t_1^*$$, $$x^{0,(k)}(\cdot) \rightarrow x^{0,*}$$ (т.к. $$E -$$ компакт). | + | Без ограничения общности, положим $$t_0^{(k)}(\cdot) \rightarrow t_0^*$$, $$t_1^{(k)}(\cdot) \rightarrow t_1^*$$, $$x^{0,(k)}(\cdot) \rightarrow x^{0,*}$$ (т.к. $$E$$ $$-$$ компакт). |
| − | 1) $$\frac{d}{dt}{\|x(t)\|}^2 = 2\langle x, f(t,\ x,\ u) \rangle \leqslant 2\|x\|\|f(t,\ x,\ u)\| \overset{\text{условие сублинейного роста}}{\leqslant} 2A\|x\|^2 + 2B\|x\| = (2A + 1) \|x\|^2 + \tilde{B}$$ | + | 1) $$\frac{d}{dt}{\|x(t)\|}^2 = 2\langle x, f(t,\ x,\ u) \rangle \leqslant 2\|x\|\|f(t,\ x,\ u)\| \overset{\text{условие сублинейного роста}}{\leqslant} 2A\|x\|^2 + 2B\|x\| = (2A + 1) \|x\|^2 + \tilde{B}$$. |
| − | Откуда | + | Откуда: |
| + | \begin{gather*} | ||
| + | \frac{d}{dt}\left(\|x(t)\|^2e^{-(2A+1)t}\right) \leqslant \tilde{B} e^{-(2A + 1)t}\|,\\ | ||
| + | \|x(t)\|^2 e^{-(2A+1)t} - \|{x(t_0)}^2\| e^{-(2A+1)t_0} \leqslant \int\limits_{t_0}^{t} \tilde{B} e^{-(2A + 1)s} ds,\\ | ||
| + | \|{x^{(k)}(t)}\|^2 \leqslant \underbrace{\|{x^{(k)}(t_0^{(k)})}\|^2 e^{(2A + 1)(t - t_0^{(k)})} + e^{(2A + 1)t} \int\limits_{t_0^{(k)}}^{t} \tilde{B} e^{-(2A + 1)s}ds}_{\text{ограниченная функция}}. | ||
| + | \end{gather*} | ||
| − | $$\ | + | Значит, $$\{x^k(\cdot)\}$$ равномерно ограничена: $$\forall k$$ $$\exists M: \|x^{(k)}\| \leqslant M$$. |
| − | $$\|{x^{(k)}( | + | Теперь покажем равностепенную непрерывность: $$\|x^{(k)}(t_2) - x^{(k)}(t_1)\| \leqslant \int\limits_{t_1}^{t_2}\|f(t,\ x^{(k)}(t),\ u^{(k)}(t)\|dt \leqslant \underbrace{(AM + B)}_{L}\underbrace{|t_2 - t_1|}_{\delta} < \varepsilon$$. |
| − | + | Тогда по теореме Арцела-Асколи: | |
| + | \begin{gather*} | ||
| + | x^{(k)}(\cdot) \rightrightarrows x^*(\cdot), | ||
| + | \end{gather*} | ||
| + | Таким образом, $$x^{(k)}\rightrightarrows x^*$$ в пространстве $$C$$. | ||
| − | + | \begin{gather*} | |
| + | \|{x^*(t_2) - x^*(t_1)}\| \leqslant L |t_2 - t_1|, | ||
| + | \end{gather*} | ||
| + | Получаем | ||
| + | \begin{gather*} | ||
| + | x^*(\cdot) \in \mathrm{Lip} \Rightarrow x^*(\cdot) \in \mathrm{AC}. | ||
| + | \end{gather*} | ||
| − | + | Всё, изложенное выше, выполняется и для $$\overline{x} = (x_0,\ x)$$. Далее для простоты записи чёрточки над $$x$$ и $$f$$ будем опускать. | |
| − | $$\ | + | 2) Докажем, что $$\forall t$$ $$\frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}(t, \overline{x}^*(t)) = \bigcup\limits_{u \in \mathcal{P}}\{\overline{f}(t,\ \overline{x},\ u)\}$$. |
| − | + | Пусть $$t$$ такое, что $$\exists$$ $$\frac{d \overline{x}^*(t)}{dt}$$. Обозначим $$\mathcal{F}_{\varepsilon, t} = \mathcal{F}_t + B_{\varepsilon}(0) \in \mathrm{conv}~\R^{n+1}$$. $$f(t,\ x,\ u) \in \mathrm{C}([T_0,\ T_1]\times B_M(0) \times \mathcal{P})$$, следовательно $$f$$ равномерно непрерывна, т.е.: | |
| − | |||
| − | Пусть $$t$$ такое, что $$\exists$$ $$\frac{d x^*(t)}{dt}$$. Обозначим $$\mathcal{F}_{\varepsilon, t} = \mathcal{F}_t + B_{\varepsilon}(0) \in \mathrm{conv}~\R^n$$. $$f(t,\ x,\ u) \in \mathrm{C}([T_0,\ T_1]\times B_M(0) \times \mathcal{P})$$, следовательно $$f$$ равномерно непрерывна, т.е.: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \forall \varepsilon > 0 \;\; \exists \delta > 0: \forall (t_1, x_1, u_1), (t_2, x_2, u_2) \in [T_0, T_1] \times B_{M}(0) \times \mathcal{P}\\ | + | \forall \varepsilon > 0 \;\; \exists \delta > 0: \forall (t_1, x_1, u_1), (t_2, x_2, u_2) \in [T_0, T_1] \times B_{M}(0) \times \mathcal{P},\\ |
| − | |t_1 - t_2| + \|{x_1 - x_2}\| + \|{u_1 - u_2}\| < \delta\\ | + | |t_1 - t_2| + \|{x_1 - x_2}\| + \|{u_1 - u_2}\| < \delta,\\ |
| − | \|{f(t_1, x_1, u_1) - f(t_2, x_2, u_2)}\| < \varepsilon | + | \|{f(t_1, x_1, u_1) - f(t_2, x_2, u_2)}\| < \varepsilon. |
\end{gather*} | \end{gather*} | ||
Возьмем $$u_1 = u_2 = u$$, тогда $$\forall (\tau, x) \in [T_0, T_1] \times B_{M}(0) \colon$$ | Возьмем $$u_1 = u_2 = u$$, тогда $$\forall (\tau, x) \in [T_0, T_1] \times B_{M}(0) \colon$$ | ||
\begin{gather*} | \begin{gather*} | ||
| − | |\tau - t| + \|{x - x^*(t)}\| < \delta | + | |\tau - t| + \|{x - x^*(t)}\| < \delta, |
| − | |||
\end{gather*} | \end{gather*} | ||
| + | \begin{gather} | ||
| + | \Delta f = \|f(\tau, x, u) - f(t, x^*, u)\| \leqslant \varepsilon, \label{ex1} | ||
| + | \end{gather} | ||
| + | |||
\begin{gather*} | \begin{gather*} | ||
| − | \forall u \in \mathcal{P}: f(\tau, x, u) = f(t, x^*, u) + \Delta f | + | \forall u \in \mathcal{P}: f(\tau, x, u) = f(t, x^*, u) + \Delta f, |
\end{gather*} | \end{gather*} | ||
| + | |||
\begin{gather*} | \begin{gather*} | ||
| − | \mathcal{F}(\tau,\ x) = \bigcup\limits_{u \in \mathcal{P}} \left\{ f(\tau,\ x,\ u) \right\} \subseteq \bigcup\limits_{u \in \mathcal{P}} \left\{ f(t,\ x^*,\ u) \right\} + B_{\varepsilon}(0) = \mathcal{F}_{\varepsilon, t}\\ | + | \mathcal{F}(\tau,\ \overline{x}) = \bigcup\limits_{u \in \mathcal{P}} \left\{ \overline{f}(\tau,\ \overline{x},\ u) \right\} \subseteq \bigcup\limits_{u \in \mathcal{P}} \left\{ \overline{f}(t,\ \overline{x}^*,\ u) \right\} + B_{\varepsilon}(0) = \mathcal{F}_{\varepsilon, t},\\ |
| − | \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\| | + | \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\|. |
\end{gather*} | \end{gather*} | ||
| + | |||
Рассмотрим неравенство: | Рассмотрим неравенство: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\| | + | \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\|. |
| + | \end{gather*} | ||
| + | |||
| + | Выберем $$\tau$$: | ||
| + | \begin{gather*} | ||
| + | \|{x^{(k)}(\tau) - x^{(k)}(t)}\| \leqslant L \|\tau - t\| < \frac{\delta}{4},\\ | ||
| + | \exists K \;\; \forall k \geqslant K \;\; \|{x^{(k)}(t) - x^{*}(t)}\| \leqslant \frac{\delta}{4},\\ | ||
| + | |\tau - t| < \mathrm{min}\{\frac{\delta}{4L},\ \frac{\delta}{2}\}. | ||
\end{gather*} | \end{gather*} | ||
| + | |||
| + | |||
| + | Тогда из \eqref{ex1} получаем: | ||
| + | \begin{gather} | ||
| + | \mathcal{F}(\tau, x^{(k)}(\tau)) \subseteq \mathcal{F}_{\varepsilon, t} \label{ex2}. | ||
| + | \end{gather} | ||
| + | |||
| + | Рассмотрим последовательность $$z^{(k)}(s) = f(s, x^{(k)}(s), u^{(k)}(s))$$, выполнено: | ||
| + | \begin{gather*} | ||
| + | \frac{x^{(k)}(t+h) - x^{(k)}(t)}{h} = \frac{1}{h} \int\limits_{t}^{t+h} \underbrace{z^{(k)}(s)}_{\in \mathcal{F}(s,\ x^{(k)}(s))} ds \in \mathcal{F}_{\varepsilon, t}. | ||
| + | \end{gather*} | ||
| + | |||
| + | Значит: | ||
| + | \begin{gather*} | ||
| + | \frac{x^{(k)}(t+h) - x^{(k)}(t)}{h} \in \mathcal{F}_{\varepsilon, t} \bigg| \lim\limits_{h \to 0} \; \lim\limits_{k \to \infty},\\ | ||
| + | \frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}_{\varepsilon, t} \; \forall \varepsilon > 0 \bigg| \lim\limits_{\varepsilon \to 0 + 0},\\ | ||
| + | \frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}(t, \overline{x}^*(t)). | ||
| + | \end{gather*} | ||
| + | |||
| + | Таким образом, $$\frac{d\overline{x}^*(t)}{dt} \overset{\text{п. в.} t}{=} \overline{f}(t, \overline{x}^*(t), u^*(t))$$. | ||
| + | |||
| + | Покажем, что множество $$\mathcal{P}^*(t) = \left\{ u \in \mathcal{P}\colon \overline{f}(t, \overline{x}^*(t), u) = \frac{d\overline{x}^*(t)}{dt} \right\}$$ измеримо по $$t$$. | ||
| + | |||
| + | $$x^*(\cdot) \in \mathrm{AC}$$, тогда $$\frac{d\overline{x}^*(t)}{dt}$$ $$-$$ измеримо. По теореме Лузина $$\frac{d\overline{x}^*}{dt} \in \mathrm{C}([T_0,\ T_1]\setminus Z),\ \mu(Z) < \tilde{\varepsilon}$$. | ||
| + | |||
| + | Рассмотрим | ||
| + | \begin{gather*} | ||
| + | t_k \in [T_0, T_1] \setminus Z, \; t_k \underset{k \rightarrow \infty}{\rightarrow} \widetilde{t}, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | u_k \in \mathcal{P}^*(t_k) \to \widetilde{u} \in \mathcal{P},\\ | ||
| + | \frac{d\overline{x}^*(t_k)}{dt} = \overline{f}(t_k, \overline{x}^*(t_k), u_k) \underset{k \rightarrow \infty}{\rightarrow} \overline{f}(\widetilde{t}, \overline{x}^*(\widetilde{t}, \widetilde{u})),\\ | ||
| + | \frac{d\overline{x}^*(t_k)}{dt} \to \frac{d\overline{x}^*(\widetilde{t})}{dt}. | ||
| + | \end{gather*} | ||
| + | Следовательно, $$\widetilde{u} \in \mathcal{P}^*(\widetilde{t})$$, получаем, что $$\mathcal{P}$$ полунепрерывная сверху. Отображение $$\mathcal{P}^*$$ измеримое, то есть существует измеримый селектор $$u^*(t) \in \mathcal{P}^*(t)$$. | ||
| + | $$\blacksquare$$ | ||
| + | |||
| + | == Список литературы == | ||
| + | * И.А. Чистяков "Лекции по оптимальному управлению", 2022 | ||
| + | * Э.Б. Ли, Л. Маркус "Основы теории оптимального управления", М.: Наука, 1972 | ||
Текущая версия на 16:31, 1 декабря 2022
Содержание
Аннотация
В этой статье будет рассмотрена теорема существования оптимального управления для нелинейной системы в $$\mathbb{R}^n$$: \begin{gather*} \dot x = f(t, x(t), u(t)) \end{gather*}
Приведём контрпримеры, демонстрирующие невозможность отыскать оптимальное управление при помощи ПМП.
Случаи, когда решения не существует
Пример 1
Множество допустимых пар $$\{x(\cdot),\ u(\cdot)\}$$ пусто: \begin{gather*} \begin{cases} \dot{x} = 0, \\ x(0) = 0,\\ x(1) = 1. \end{cases} \end{gather*}
Пример 2
Ограничивающее множество $$\mathcal{P} \notin \mathrm{conv}~\R$$
\begin{gather*} \begin{cases} \dot{x} = u, & u \in \R, \\ x(0) = 1,\\ x(1) = 0. \end{cases} \end{gather*} \begin{gather*} J = \int_0^1 x^2(t) dt \to \inf. \end{gather*}
Перейдём к расширенной системе:
\begin{equation*} \begin{cases} \dot{x_0} = x_1^2, \\ \dot{x_1} = u. \end{cases} \end{equation*}
Тогда функция Гамильтона-Понтрягина примет вид: \begin{gather*} \mathcal{H} = \psi_0 x_1^2 + \psi_1 u, \end{gather*} \begin{gather*} \begin{cases} \dot{\psi}_0 = 0, \\ \dot{\psi}_1 = -2 \psi_0 x_1. \end{cases} \end{gather*}
В этом случае $$u = \pm \infty$$. Рассмотрим управления $$u_k$$: \begin{gather*} u_k(t) = \begin{cases} -k, &\; t \in \left[0, \frac{1}{k}\right],\\ 0, &\; \text{иначе}. \end{cases} \end{gather*}
\begin{gather*} x_k(t) = \begin{cases} 1-kt,\; t \in \left[0, \frac{1}{k}\right],\\ 0,\; \text{иначе}. \end{cases} \end{gather*}
Тогда $$\mathrm{inf}J(\cdot) = 0$$, т.к. $$J(\cdot) \geqslant 0.$$
\begin{gather*} J\left(u_k(\cdot)\right) = \int\limits_0^{\frac{1}{k}}(1 - kt)^2 dt = \frac{1}{3k} \underset{k \rightarrow +\infty}{\rightarrow} 0. \end{gather*}
Но $$\mathrm{inf}J(\cdot)$$ не достигается в силу непрерывности $$x(\cdot)$$.
Пример 3
Множество обобщенных скоростей (векторграмма) $$\mathcal{F}(t,\ \overline{x}) \notin \mathrm{conv}~\R^{n+1}$$
\begin{gather*} \begin{cases} \dot{x} = u, \; |u| \leqslant 1, \\ x(0) = x(1) = 0. \end{cases} \end{gather*}
\begin{gather*} J = \int_0^1 [x^2(t) + (1 - u^2(t))^2] dt \rightarrow \underset{u(\cdot)}{\mathrm{inf}}. \end{gather*}
\begin{gather*} \mathcal{H} = \psi_0 (u_1^2 + (1 - u^2)^2) + \psi_1 u, \\ \begin{cases} \dot{\psi}_0 = 0, \\ \dot{\psi}_1 = -2 \psi_0 x_1. \end{cases} \end{gather*}
\begin{gather*} u_k(t) = \begin{cases} 1, \; t \in \left[\frac{2j}{2k}, \frac{2j + 1}{2k}\right],\\ -1, \; t \in \left[\frac{2j + 1}{2k}, \frac{2j + 2}{2k}\right]. \end{cases} \end{gather*}
\begin{gather*} x_k(t) = \begin{cases} t - \frac{2j}{2k}, \; t \in \left[\frac{2j}{2k}, \frac{2j + 1}{2k}\right],\\ -t + \frac{2j + 2}{2k}, \; t \in \left[\frac{2j + 1}{2k}, \frac{2j + 2}{2k}\right]. \end{cases} \end{gather*}
\begin{gather*} J\left(u_k(\cdot)\right) = k \int\limits_0^{\frac{1}{k}} x_k^2(t) dt = 2k \int\limits_0^{\frac{1}{2k}} t^2 dt = \frac{1}{3(2k)^2} \underset{k \rightarrow +\infty}{\rightarrow} 0. \end{gather*}
Таким образом, $$\mathrm{inf}J(\cdot)$$ не достигается даже при ограничении $$|u| \leqslant 1$$.
Замечание: В отличие от Примера 2 ПМП даёт результат, но неправильный.
Пример 4
$$E = \{e = (t_0,\ x^0, t_1, x^1): \varphi(e) = 0\}$$ $$-$$ компакт, $$\overline{\varphi} = (\varphi_0,\ \varphi)$$
$$\overline{\varphi} \notin C(E)$$ \begin{gather*} \begin{cases} \dot{x} = u, \; |u| \leqslant 1,\\ x(0) = 0,\\ t_1 x(t_1) = 1. \end{cases} \end{gather*}
\begin{gather*} J = x(t_1) \rightarrow \mathrm{inf}. \end{gather*}
\begin{gather*} \mathcal{H} = \psi_1 u, \end{gather*}
\begin{gather*} u^* = \begin{cases} 1, \; \psi_1 > 0, \\ [-1, 1],\; \psi_1 = 0, \\ -1, \;\psi_1 < 0. \end{cases} \end{gather*} Отсюда: \begin{gather*} \begin{matrix} \dot{\psi_1} = 0, \\ \psi_1[0] = - \lambda_3 \; \mathcal{H}\vert_{t = t_0} = \lambda_2, \\ \psi_1[t_1] = \lambda_0 + \lambda_1 t_1 \; \mathcal{H} \vert_{t = t_1} = -\lambda_1 x(t_1). \end{matrix} \end{gather*}
Фиксируем $$\tau > 0$$: \begin{gather*} u(t) = \begin{cases} 0, \; t \in [0, \tau], \\ 1, \; t > \tau. \end{cases} \end{gather*}
\begin{gather*} x(t) = \begin{cases} 0, \; t \in [0, \tau], \\ t - \tau, \; t > \tau. \end{cases} \end{gather*}
\begin{gather*} x(t_1) t_1 = 1 \Rightarrow t_1^2 - \tau t_1 - 1 = 0,\\ t_1 = \frac{\tau + \sqrt{\tau^2 + 4}}{2}. \end{gather*}
При $$\tau \rightarrow +\infty$$: $$t_1 \rightarrow +\infty$$ и $$x(t_1) = \frac{1}{t_1} \rightarrow 0$$. Следовательно, $$\mathrm{inf}J(\cdot) = 0$$ не достигается.
Теорема о существовании оптимального управления
Пусть $$\dot x = f(t, x(t), u(t)),\ u(t) \in \mathcal{P}$$, где $$f$$ удовлетворяет описанию, обозначенному в итоговых условиях на функцию: \begin{gather*} \varphi_0(e) \rightarrow \infty,\\ \varphi_1(e) = \varphi_2(e) = \ldots = \varphi_k(e) = 0. \end{gather*} Пусть также:
- Множество допустимых пар $$\{x(\cdot),\ u(\cdot)\}$$ не пусто, то есть $$S^1 = \{(t_0,\ t_1,\ x^0,\ u(\cdot)) \in S | \varphi(e) = 0,\ e = e(t_0,\ t_1,\ x^0,\ u(\cdot))\} \neq \emptyset$$. Пример 1.
- $$\mathcal{P} \in \mathbb{R}^m$$. Пример 2.
- $$\mathcal{F}(t,\ \overline{x}) = \bigcup\limits_{u \in \mathcal{P}}\{\overline{f}(t,\ \overline{x},\ u)\} \in \mathrm{conv}~\R^{n+1}$$, $$\mathcal{F}(t,\ \overline{x})$$ $$-$$ множество возможных скоростей (векторграмма). Пример 3.
- $$E = \{e = (t_0,\ x^0, t_1, x^1) \in \mathbb{R}^{2n+2}: \varphi(e) = 0\}$$ $$-$$ компакт, $$\overline{\varphi} = (\varphi_0,\ \varphi) \in C(E)$$. Пример 4.
Тогда решение задачи оптимального управления существует ($$\exists u^*$$ $$-$$ измеримое).
Замечание: Если $$f(t,\ x,\ u) = f^0(t,\ x) + g(t,\ x)\cdot u$$, то условие $$3$$ можно заменить на $$\mathcal{P} \in \mathrm{conv}~\R^{n+1}$$.
Доказательство
Пусть $$\varphi_* = \mathrm{inf}\{\varphi_0(e): e = e(s), s \in S^1\}$$, $$\varphi_* > -\infty$$, т.к. $$\overline{\varphi} \in C(E)$$, $$E$$ $$-$$ компакт. По определению инфимума: \begin{gather*} \forall \varepsilon = \frac{1}{k} \;\; \exists (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}): \;\; \varphi_* \leqslant \varphi_0(e^{(k)}) \leqslant \varphi_* + \frac{1}{k},\ e^{(k)} = (t_0^{(k)},\ x^{0,\ (k)}, t_1^{(k)}, u(\cdot)^{(k)}). \end{gather*}
План доказательства:
- Доказать, что $$x^{(k)}(\cdot) \underset{k \rightarrow \infty}{\rightarrow} x^*(\cdot)$$ в пространстве $$C$$.
- Доказать, что $$x^*(\cdot)$$ порождается некоторым управлением $$u^*(\cdot)$$.
Без ограничения общности, положим $$t_0^{(k)}(\cdot) \rightarrow t_0^*$$, $$t_1^{(k)}(\cdot) \rightarrow t_1^*$$, $$x^{0,(k)}(\cdot) \rightarrow x^{0,*}$$ (т.к. $$E$$ $$-$$ компакт).
1) $$\frac{d}{dt}{\|x(t)\|}^2 = 2\langle x, f(t,\ x,\ u) \rangle \leqslant 2\|x\|\|f(t,\ x,\ u)\| \overset{\text{условие сублинейного роста}}{\leqslant} 2A\|x\|^2 + 2B\|x\| = (2A + 1) \|x\|^2 + \tilde{B}$$.
Откуда: \begin{gather*} \frac{d}{dt}\left(\|x(t)\|^2e^{-(2A+1)t}\right) \leqslant \tilde{B} e^{-(2A + 1)t}\|,\\ \|x(t)\|^2 e^{-(2A+1)t} - \|{x(t_0)}^2\| e^{-(2A+1)t_0} \leqslant \int\limits_{t_0}^{t} \tilde{B} e^{-(2A + 1)s} ds,\\ \|{x^{(k)}(t)}\|^2 \leqslant \underbrace{\|{x^{(k)}(t_0^{(k)})}\|^2 e^{(2A + 1)(t - t_0^{(k)})} + e^{(2A + 1)t} \int\limits_{t_0^{(k)}}^{t} \tilde{B} e^{-(2A + 1)s}ds}_{\text{ограниченная функция}}. \end{gather*}
Значит, $$\{x^k(\cdot)\}$$ равномерно ограничена: $$\forall k$$ $$\exists M: \|x^{(k)}\| \leqslant M$$.
Теперь покажем равностепенную непрерывность: $$\|x^{(k)}(t_2) - x^{(k)}(t_1)\| \leqslant \int\limits_{t_1}^{t_2}\|f(t,\ x^{(k)}(t),\ u^{(k)}(t)\|dt \leqslant \underbrace{(AM + B)}_{L}\underbrace{|t_2 - t_1|}_{\delta} < \varepsilon$$.
Тогда по теореме Арцела-Асколи: \begin{gather*} x^{(k)}(\cdot) \rightrightarrows x^*(\cdot), \end{gather*} Таким образом, $$x^{(k)}\rightrightarrows x^*$$ в пространстве $$C$$.
\begin{gather*} \|{x^*(t_2) - x^*(t_1)}\| \leqslant L |t_2 - t_1|, \end{gather*} Получаем \begin{gather*} x^*(\cdot) \in \mathrm{Lip} \Rightarrow x^*(\cdot) \in \mathrm{AC}. \end{gather*}
Всё, изложенное выше, выполняется и для $$\overline{x} = (x_0,\ x)$$. Далее для простоты записи чёрточки над $$x$$ и $$f$$ будем опускать.
2) Докажем, что $$\forall t$$ $$\frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}(t, \overline{x}^*(t)) = \bigcup\limits_{u \in \mathcal{P}}\{\overline{f}(t,\ \overline{x},\ u)\}$$.
Пусть $$t$$ такое, что $$\exists$$ $$\frac{d \overline{x}^*(t)}{dt}$$. Обозначим $$\mathcal{F}_{\varepsilon, t} = \mathcal{F}_t + B_{\varepsilon}(0) \in \mathrm{conv}~\R^{n+1}$$. $$f(t,\ x,\ u) \in \mathrm{C}([T_0,\ T_1]\times B_M(0) \times \mathcal{P})$$, следовательно $$f$$ равномерно непрерывна, т.е.: \begin{gather*} \forall \varepsilon > 0 \;\; \exists \delta > 0: \forall (t_1, x_1, u_1), (t_2, x_2, u_2) \in [T_0, T_1] \times B_{M}(0) \times \mathcal{P},\\ |t_1 - t_2| + \|{x_1 - x_2}\| + \|{u_1 - u_2}\| < \delta,\\ \|{f(t_1, x_1, u_1) - f(t_2, x_2, u_2)}\| < \varepsilon. \end{gather*} Возьмем $$u_1 = u_2 = u$$, тогда $$\forall (\tau, x) \in [T_0, T_1] \times B_{M}(0) \colon$$ \begin{gather*} |\tau - t| + \|{x - x^*(t)}\| < \delta, \end{gather*} \begin{gather} \Delta f = \|f(\tau, x, u) - f(t, x^*, u)\| \leqslant \varepsilon, \label{ex1} \end{gather}
\begin{gather*} \forall u \in \mathcal{P}: f(\tau, x, u) = f(t, x^*, u) + \Delta f, \end{gather*}
\begin{gather*} \mathcal{F}(\tau,\ \overline{x}) = \bigcup\limits_{u \in \mathcal{P}} \left\{ \overline{f}(\tau,\ \overline{x},\ u) \right\} \subseteq \bigcup\limits_{u \in \mathcal{P}} \left\{ \overline{f}(t,\ \overline{x}^*,\ u) \right\} + B_{\varepsilon}(0) = \mathcal{F}_{\varepsilon, t},\\ \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\|. \end{gather*}
Рассмотрим неравенство: \begin{gather*} \|{x^{(k)}(\tau) - x^*(t)}\| \leqslant \|{x^{(k)}(\tau) - x^{(k)}(t)}\| + \|{x^{(k)}(t) - x^*(t)}\|. \end{gather*}
Выберем $$\tau$$: \begin{gather*} \|{x^{(k)}(\tau) - x^{(k)}(t)}\| \leqslant L \|\tau - t\| < \frac{\delta}{4},\\ \exists K \;\; \forall k \geqslant K \;\; \|{x^{(k)}(t) - x^{*}(t)}\| \leqslant \frac{\delta}{4},\\ |\tau - t| < \mathrm{min}\{\frac{\delta}{4L},\ \frac{\delta}{2}\}. \end{gather*}
Тогда из \eqref{ex1} получаем:
\begin{gather}
\mathcal{F}(\tau, x^{(k)}(\tau)) \subseteq \mathcal{F}_{\varepsilon, t} \label{ex2}.
\end{gather}
Рассмотрим последовательность $$z^{(k)}(s) = f(s, x^{(k)}(s), u^{(k)}(s))$$, выполнено: \begin{gather*} \frac{x^{(k)}(t+h) - x^{(k)}(t)}{h} = \frac{1}{h} \int\limits_{t}^{t+h} \underbrace{z^{(k)}(s)}_{\in \mathcal{F}(s,\ x^{(k)}(s))} ds \in \mathcal{F}_{\varepsilon, t}. \end{gather*}
Значит: \begin{gather*} \frac{x^{(k)}(t+h) - x^{(k)}(t)}{h} \in \mathcal{F}_{\varepsilon, t} \bigg| \lim\limits_{h \to 0} \; \lim\limits_{k \to \infty},\\ \frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}_{\varepsilon, t} \; \forall \varepsilon > 0 \bigg| \lim\limits_{\varepsilon \to 0 + 0},\\ \frac{d \overline{x}^*(t)}{dt} \in \mathcal{F}(t, \overline{x}^*(t)). \end{gather*}
Таким образом, $$\frac{d\overline{x}^*(t)}{dt} \overset{\text{п. в.} t}{=} \overline{f}(t, \overline{x}^*(t), u^*(t))$$.
Покажем, что множество $$\mathcal{P}^*(t) = \left\{ u \in \mathcal{P}\colon \overline{f}(t, \overline{x}^*(t), u) = \frac{d\overline{x}^*(t)}{dt} \right\}$$ измеримо по $$t$$.
$$x^*(\cdot) \in \mathrm{AC}$$, тогда $$\frac{d\overline{x}^*(t)}{dt}$$ $$-$$ измеримо. По теореме Лузина $$\frac{d\overline{x}^*}{dt} \in \mathrm{C}([T_0,\ T_1]\setminus Z),\ \mu(Z) < \tilde{\varepsilon}$$.
Рассмотрим \begin{gather*} t_k \in [T_0, T_1] \setminus Z, \; t_k \underset{k \rightarrow \infty}{\rightarrow} \widetilde{t}, \end{gather*} \begin{gather*} u_k \in \mathcal{P}^*(t_k) \to \widetilde{u} \in \mathcal{P},\\ \frac{d\overline{x}^*(t_k)}{dt} = \overline{f}(t_k, \overline{x}^*(t_k), u_k) \underset{k \rightarrow \infty}{\rightarrow} \overline{f}(\widetilde{t}, \overline{x}^*(\widetilde{t}, \widetilde{u})),\\ \frac{d\overline{x}^*(t_k)}{dt} \to \frac{d\overline{x}^*(\widetilde{t})}{dt}. \end{gather*} Следовательно, $$\widetilde{u} \in \mathcal{P}^*(\widetilde{t})$$, получаем, что $$\mathcal{P}$$ полунепрерывная сверху. Отображение $$\mathcal{P}^*$$ измеримое, то есть существует измеримый селектор $$u^*(t) \in \mathcal{P}^*(t)$$. $$\blacksquare$$
Список литературы
- И.А. Чистяков "Лекции по оптимальному управлению", 2022
- Э.Б. Ли, Л. Маркус "Основы теории оптимального управления", М.: Наука, 1972