Сумма двух эллипсоидов. Внутренние и внешние оценки: различия между версиями
Lidia (обсуждение | вклад) |
Lidia (обсуждение | вклад) |
||
| (не показано 47 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | |||
| − | |||
Данная глава посвящена рассмотрению суммы двух эллипсоидов, будут выведены внутренние и внешние оценки. | Данная глава посвящена рассмотрению суммы двух эллипсоидов, будут выведены внутренние и внешние оценки. | ||
Здесь и далее в главе рассматриваются исключительно невырожденные эллипсоиды. | Здесь и далее в главе рассматриваются исключительно невырожденные эллипсоиды. | ||
\begin{gather*} | \begin{gather*} | ||
| − | \ | + | \mathcal{E}_{1} = \mathcal{E} (a_1, Q_{1}); \\ |
| − | \ | + | \mathcal{E}_{2} = \mathcal{E} (a_2, Q_{2}). \\ |
\end{gather*} | \end{gather*} | ||
| − | == | + | ==Определения== |
| − | === | + | ===Сумма по Минковскому=== |
| − | '''(a)''' | + | ''Пусть даны два множества $$\mathcal{H}_1, \mathcal{H}_2 \subset \mathbb{R}^n$$, геометрической суммой (суммой по Минковскому) называется следующая сумма: |
| + | \begin{equation} | ||
| + | \mathcal{H}_1 + \mathcal{H}_2 = \bigcup_{h_1 \in \mathcal{H}_1} \bigcup_{h_2 \in \mathcal{H}_2} \{ h_1 + h_2\}. | ||
| + | \end{equation} '' | ||
| + | |||
| + | ===Внешняя и внутренняя оценки=== | ||
| + | ''Пусть даны два эллипсоида $$\mathcal{E}_{1} = \mathcal{E} (a_1, Q_{1}), \mathcal{E}_{2} = \mathcal{E} (a_2, Q_{2})$$, будем рассматривать их сумму $$\mathcal{E}_{1} + \mathcal{E}_{2}$$. Внешней оценкой будем называть $$\mathcal{E}^{(+)}$$: | ||
| + | \begin{equation} | ||
| + | \mathcal{E}_{1} + \mathcal{E}_{2} \subseteq \mathcal{E}^{(+)}; | ||
| + | \end{equation} | ||
| + | ''Внутренней оценкой будем называть $$\mathcal{E}^{(-)}$$: | ||
| + | \begin{equation} | ||
| + | \mathcal{E}^{(-)} \subseteq \mathcal{E}_{1} + \mathcal{E}_{2}. | ||
| + | \end{equation} | ||
| + | |||
| + | ==Внешние оценки== | ||
| + | ===Леммы=== | ||
| + | '''Лемма 1'''<br> | ||
| + | |||
| + | '''(a)''' Рассмотрим эллипсоид \( \mathcal{E} = \mathcal{E}(a_1 + a_2, Q(p)) \) для любых \( p > 0 \), тогда он оценивает сумму \(\mathcal{E}_1 + \mathcal{E}_2\) следующим образом: | ||
\[ | \[ | ||
| − | \ | + | \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E} (a_1 + a_2,Q(p)), |
\] | \] | ||
| − | для любого \(p > 0 \) \[\] | + | для любого \(p > 0 \), если \( Q(p) = (1 + p^{-1})Q_1 + (1 + p)Q_2\), а \( Q_1, Q_2 \) конфигурационные матрицы (симметричные и невырожденные) первого и второго эллипсоидов соответственно.\[\] |
'''(b)''' По данному вектору \( l \in R^n, \|l\| = 1\) выражение | '''(b)''' По данному вектору \( l \in R^n, \|l\| = 1\) выражение | ||
\[ | \[ | ||
| − | p = | + | p = |
| + | \langle Q_1l,l \rangle^{\frac{1}{2}} \langle Q_2l,l \rangle^{-\frac{1}{2}} | ||
\] определяет параметр \(p \in \Pi^{+}\), такой что | \] определяет параметр \(p \in \Pi^{+}\), такой что | ||
| − | \[ \rho(l|\ | + | \[ \rho(l|\mathcal{E} (a_1 + a_2,Q(p))) = \rho(l|\mathcal{E}(a_1,Q_1) + \mathcal{E}(a_2,Q_2)).\] |
| − | И обратно, по данному параметру \(p \in \Pi^{+}\), существует вектор \( l \in R^n, \|l\| = 1\), удовлетворяющий | + | И обратно, по данному параметру \(p \in \Pi^{+}\), существует вектор \( l \in R^n, \|l\| = 1\), удовлетворяющий вышеуказанным равенствам.<br> |
| − | ===Лемма 2 | + | Обратим внимание, что \( \Pi^{+} = \left[ \lambda_{min}^{1/2}, \lambda_{max}^{1/2} \right] \),где \[\ \lambda_{min} = \lambda_{1} \leq \lambda_{2} \leq ... \leq \lambda_{n} = \lambda_{max}, \] корни уравнения \[ det(Q_1 - \lambda Q_2) = 0 .\] |
| + | |||
| + | '''Лемма 2'''<br> | ||
| + | Пусть \( C \) положительно определенная симметричная матрица с элементами \( {c_{ij}} \).<br> | ||
Зафиксируем вектор \( l \in R^n, \|l\| = 1\) и предположим, что для некоторого \( m \in [0,n]\) имеем | Зафиксируем вектор \( l \in R^n, \|l\| = 1\) и предположим, что для некоторого \( m \in [0,n]\) имеем | ||
\[ | \[ | ||
| − | l_j = 0, если j \in \overline{1,m}\\ | + | l_j = 0,\text{ }если\text{ }j \in \overline{1,m};\\ |
| − | l_j \neq 0, если j = \overline{m+1,n} | + | l_j \neq 0,\text{ }если\text{ } j = \overline{m+1,n}. |
\] | \] | ||
| − | Помимо этого будем считать, что \ | + | Помимо этого будем считать, что $$\mathcal{E}_1 = \mathcal{E}(0,Q_1), \mathcal{E}_2 = \mathcal{E}(0,Q_2)$$, а матрицы \(Q_1, Q_2, Q\) диагональные. Если верно следующее: |
\[ | \[ | ||
| − | \ | + | \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}(0, Q), |
\] | \] | ||
| − | а также \[\rho(l|\ | + | а также \[\rho(l|\mathcal{E}(0, Q)) = \rho(l|\mathcal{E}_1 + \mathcal{E}_2) .\] |
Тогда | Тогда | ||
\[ | \[ | ||
| − | c_{ij} \text{ для всех } i \neq j, i \in \overline{m+1,n} | + | c_{ij} = 0, \text{ для всех } i \neq j,\text{ } i \in \overline{m+1,n}. |
\] | \] | ||
| − | + | ||
| − | Возьмем эллипсоид \(\ | + | '''Лемма 3'''<br> |
| + | |||
| + | Возьмем эллипсоид \(\mathcal{E}(0, C)\) вместе с \(\mathcal{E}_1 = \mathcal{E}(0,Q_1), \mathcal{E}_2 = \mathcal{E}(0,Q_2),\) предполагая \(Q_1 \text{ и } Q_2 \) диагональными. Также считаем данным вектор \( l \in R^n, \|l\| = 1\), параметр \(p\) считается известным ввиду Леммы 1. Тогда: | ||
\[ | \[ | ||
| − | \ | + | \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}(0, Q(p)) |
\] | \] | ||
и | и | ||
\[ | \[ | ||
| − | \rho(l|\ | + | \rho(l|\mathcal{E}(0, Q(p))) = \rho(l|\mathcal{E}_1 + \mathcal{E}_2), |
\] | \] | ||
тогда | тогда | ||
\[ | \[ | ||
| − | \ | + | \mathcal{E}(0,Q(p)) = \mathcal{E}(0, C)\text{ и }p\in\Pi^{+} . |
\] | \] | ||
| − | ==Теоремы== | + | |
| − | + | ===Теоремы=== | |
| − | Предполагая, что \(\ | + | '''Теорема 1'''<br> |
| + | Предполагая, что \(\mathcal{E}_1 = \mathcal{E}(a_1,Q_1), \mathcal{E}_2 = \mathcal{E}(a_2,Q_2),\) предполагая \(Q_1 \text{ и } Q_2 \) положительно определенными, а также \(Q(p)\) определенным в соответствии с Леммой 1. | ||
<br> | <br> | ||
| − | Тогда | + | Тогда минимальное по включению множество, оценивающее сумму \( \mathcal{E}_1 + \mathcal{E}_2\), состоит из эллипсоидов вида \( \mathcal{E}(a_1 + a_2, Q(p)), где \text{ }p\in\Pi^{+}.\) |
| + | |||
| + | '''Доказательство'''<br> | ||
| + | Не ограничивая общности, ссылаясь на Лемму из первого раздела, мы можем предложить, что все центры эллипсоидов находятся в нуле, т.е.\(a_1 = a_2 = 0\).<br> | ||
| + | Пусть есть такой эллипсоид, что \( \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q)\).Давайте найдем параметр \(p\), такой, чтобы эллипсоид \(\mathcal{E}(0, Q(p))\) был зажат между \(\mathcal{E}(0, Q)\) и \( \mathcal{E}_1 + \mathcal{E}_2 \). Итого мы имеем | ||
| + | \[ | ||
| + | \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q(p)) \subseteq \mathcal{E}(0, Q). | ||
| + | \] | ||
| + | Мы можем считать, что \(\mathcal{E}(0, Q)\) касательно к \(\mathcal{E}_1 + \mathcal{E}_2\), предполагая существование вектора \( l = \overline l \in R^n, \|\overline l\| = 1\), такое, что | ||
| + | \[ | ||
| + | \rho(\overline l|\mathcal{E}(0, Q)) = \rho(\overline l|\mathcal{E}_1 + \mathcal{E}_2). | ||
| + | \] | ||
| + | Давайте теперь выберем обратимую матрицу T такую, чтобы матрицы \( Q^{*}_1 = T'Q^{*}_1T ,Q^{*}_2 = T'Q^{*}_2T\) были бы обе диагональными. Существование подобной трансформационной матрицы T следует из результатов Линейной Алгебры и теории матриц. | ||
| + | <br> | ||
| + | Преобразование T не будет нарушать следующего соотношения: \( \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q^{*})\), таким образом с конфигурационной матрицей \( Q^{*} = T'QT\) будет справедливо следующее | ||
| + | \[ | ||
| + | \mathcal{E}(0, Q^{*}_1) + \mathcal{E}(0, Q^{*}_2) \subseteq \mathcal{E}(0, Q^{*}) . | ||
| + | \] | ||
| + | Пользуясь отображением \( l = T z \) можно преобразовать тождество | ||
| + | \[ | ||
| + | (\overline l, Q \overline l)^{\frac{1}{2}} = (\overline l, Q_1 \overline l)^{\frac{1}{2}} + (\overline l, Q_2 \overline l)^{\frac{1}{2}} | ||
| + | \] | ||
| + | |||
| + | к виду | ||
| + | \[ | ||
| + | (\overline z, Q^{*} \overline z)^{\frac{1}{2}} = (\overline z, Q^{*}_1 \overline z)^{\frac{1}{2}} + (\overline z, Q^{*}_2 \overline z)^{\frac{1}{2}}, | ||
| + | \] | ||
| + | |||
| + | где \(\overline z = T^{-1} \overline l \) | ||
| + | Далее можно будут справедливыми следующие преобразования: | ||
| + | |||
| + | \[ | ||
| + | \overline p = (\overline z, Q^{*}_1 \overline z)^{\frac{1}{2}} (\overline z, Q^{*}_2 \overline z)^{-\frac{1}{2}}; | ||
| + | \] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | \[ | ||
| + | Q^{*}(\overline p) = (1 + \overline p^{-1})Q^{*}_1 + (1 + \overline p)Q^{*}_2. | ||
| + | \] | ||
| + | Приходим к соотношению | ||
| + | |||
| + | \[ | ||
| + | \mathcal{E}(0, Q^{*}_1) + \mathcal{E}(0, Q^{*}_2) \subseteq \mathcal{E}(0, Q^{*}(\overline p)); | ||
| + | \] | ||
| + | |||
| + | |||
| + | \[ | ||
| + | \rho(\overline z|\mathcal{E}(0, Q^{*}_1)) +\rho(\overline z|\mathcal{E}(0, Q^{*}_2)) = \rho(\overline z|\mathcal{E}(0, Q^{*}(\overline p)) = \rho(\overline z|\mathcal{E}(0, Q^{*}). | ||
| + | \] | ||
| + | |||
| + | Из Леммы 3 | ||
| + | Существует вектор \( z^{*}\) удовлетворяющий следующему: | ||
| + | \[ | ||
| + | \rho(z^{*}|\mathcal{E}(0, Q^{*}(\overline p))) \gt \rho(z^{*}|\mathcal{E}(0, Q^{*})) . | ||
| + | \] | ||
| + | |||
| + | Очевидно , что вектора \( z^{*}\) и \(\overline z \) неколлинеарны. Определим пространство Z как пространство, натянутое на данные векторы. А \(\mathcal{E}_z (0, Q) \) есть проекция эллипсоида на пространство Z. | ||
| + | |||
| + | \[ | ||
| + | \mathcal{E}_z (0, Q^{*}) \subseteq \mathcal{E}_z (0, Q^{*}(\overline p)) ; | ||
| + | \] | ||
| + | |||
| + | \[ | ||
| + | \rho(\overline z|\mathcal{E}_z (0, Q^{*})) = \rho(\overline z|\mathcal{E}_z (0, Q^{*}(\overline p))) = \rho(\overline z|\mathcal{E}_z (0, Q^{*}_1) + \mathcal{E}_z (0, Q^{*})_2). | ||
| + | \] | ||
| + | |||
| + | Из результатов Леммы 3 \( \mathcal{E}_z (0, Q^{*}) = \mathcal{E}_z (0, Q^{*}(p)) \). $$\blacksquare$$ | ||
| + | |||
| + | ==Внутренние оценки== | ||
| + | Пусть даны эллипсоиды $$\mathcal{E}(a_1, Q_1), \mathcal{E}(a_2, Q_2), Q_1 > 0, Q_2 > 0$$, рассмотрим матрицу $$Q[S]$$ | ||
| + | \begin{equation} | ||
| + | Q[S] = S^{-1}[(SQ_1S')^{\frac{1}{2}} + (SQ_2S')^{\frac{1}{2}}]^2S'^{-1}, | ||
| + | \end{equation} | ||
| + | и $$S \in \Sigma$$, где | ||
| + | \begin{equation} | ||
| + | \Sigma = \{S \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n) : S' = S, |S| \neq 0\}. | ||
| + | \end{equation} | ||
| + | |||
| + | ===Леммы=== | ||
| + | '''Лемма 1'''<br> | ||
| + | |||
| + | Эллипсоид $$\mathcal{E} = \mathcal{E}(a_1 + a_2, Q[S]) $$ является внутренним приближением суммы (по Минковскому) $$\mathcal{E}_1 + \mathcal{E}_2$$, а именно для любого $$S \in \Sigma:$$ | ||
| + | \begin{equation} | ||
| + | \mathcal{E}[S] = \mathcal{E}(a_1 + a_2, Q[S]) \subseteq \mathcal{E}_1 + \mathcal{E}_2. | ||
| + | \end{equation} | ||
| + | Для любого $$S \in \Sigma$$ существует вектор $$l:\|l\| = 1$$, такой, что при $$l = l^*$$ выполняется равенство | ||
| + | \begin{equation}\label{eq1} | ||
| + | \rho(l|\mathcal{E}(a_1 + a_2, Q[S])) = \rho(l|\mathcal{E}_1) + \rho(l|\mathcal{E}_2). | ||
| + | \end{equation} | ||
| + | И наоборот, для любого $$l \in \mathbb{R}^n, \|l\| = 1$$, существует матрица $$S^* \in \Sigma$$: при $$S = S^*$$ выполняется равенство \eqref{eq1}. | ||
| + | |||
| + | ===Теоремы=== | ||
| + | '''Теорема 1'''<br> | ||
| + | |||
| + | Рассмотрим несколько различных эллипсоидов подобного вида: $$\mathcal{E}(a_1 + a_2, Q[S]), S \in \Sigma$$, порожденных различными матрицами $$Q[S]$$, тогда множество внутренних оценок максимального включения суммы эллипсоидов $$\mathcal{E}_1 + \mathcal{E}_2$$ состоит из эллипсоидов вида $$\mathcal{E}(a_1 + a_2, Q[S]), S \in \Sigma$$. | ||
| + | |||
| + | '''Доказательство'''<br> | ||
| + | |||
| + | Как и в теореме о внешних оценках предположим, что $$a_1 = a_2 = 0.$$ | ||
| + | |||
| + | Для того, чтобы доказать максимальность $$\mathcal{E}(0, Q[S])$$, мы должны показать, что для любого эллипсоида $$\mathcal{E}(0, Q)$$ из того, что $$\mathcal{E}(0, Q[S]) \subseteq \mathcal{E}(0, Q) \subseteq \mathcal{E}_1 + \mathcal{E}_2$$ следует, что $$Q[S] = Q.$$ | ||
| + | |||
| + | |||
| + | Согласно Лемме 1 о внутренних оценках существует вектор $$l:\|l\| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \eqref{eq1}. | ||
| + | |||
| + | Пусть $$z = Q_2^{-\frac{1}{2}}l^*.$$ Существует такая обратимая матрица $$B \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n)$$, которая отображает $$i$$-ый единичный вектор $$e_i \in \mathbb{R}^n$$ в $$Q_2^{-\frac{1}{2}}z_i \in \mathbb{R}^n$$, для любых $$i = 1, ..., n.$$ Это приводит к | ||
| + | \begin{equation}\label{eq2} | ||
| + | \rho(l, \mathcal{E}(0, B'Q[S]B)) \leq \rho(l, \mathcal{E}(0, B'QB)) \leq \rho(l, B'\mathcal{E}_1) + \rho(l, B'\mathcal{E}_2), | ||
| + | \end{equation} | ||
| + | для любых $$l \in \mathbb{R}^n$$. Это означает, что диагональные элементы $$B'Q[S]B$$ и $$B'QB$$ совпадают. | ||
| + | |||
| + | Подставляя $$l = e_i + e_j, i \neq j, $$ получим | ||
| + | \begin{equation} | ||
| + | q_{ii}^{(+)} + 2q_{ij}^{(+)} + q_{jj}^{(+)} \leq q_{ii} + 2q_{ij} + q_{jj}, | ||
| + | \end{equation} | ||
| + | для произвольных фиксированных $$i$$ и $$j$$, где $$q_{kr}^{(+)}$$ и $$q_{kr}$$ обозначают элементы в $$k$$-ом ряду и $$r$$-ом столбце матриц $$B'Q[S]B$$ и $$B'QB$$ соответственно. Т.к. диагональные элементы равны, получим: $$q_{ij}^{(+)} \leq q_{ij}$$. | ||
| + | |||
| + | Подставляя $$l = e_i - e_j $$ в \eqref{eq2} приходим к обратному неравенству. Следовательно, $$B'Q[S]B = B'QB$$ и благодаря обратимости $$B$$, получаем, что $$Q[S] = Q.$$ $$\blacksquare$$ | ||
| + | |||
| + | ==Примеры== | ||
| + | '''Пример 1'''<br> | ||
| + | \[ | ||
| + | a_1 = (3, 2), a_2 = (1, -1), | ||
| + | \] | ||
| + | \[ | ||
| + | Q_1 = \begin{pmatrix} 2 & 3\\ 2 & 7 \end{pmatrix}, | ||
| + | Q_2 = \begin{pmatrix} 3 & 2\\ 2 & 2 \end{pmatrix}. | ||
| + | \] | ||
| + | |||
| + | [[Файл:Sum2.png|center|Сумма эллипсоидов]] | ||
| + | [[Файл:Ext2.png|600px|left|Внешняя аппроксимация]] | ||
| + | [[Файл:Int2.png|600px|right|Внутренняя аппроксимация]] | ||
| + | |||
| + | |||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | |||
| + | |||
| + | |||
| + | '''Пример 2'''<br> | ||
| + | \[ | ||
| + | a_1 = (0, 0), a_2 = (1, -1), a_3 = (-2, 2), | ||
| + | \] | ||
| + | \[ | ||
| + | Q_1 = \begin{pmatrix} 2 & 1\\ 1 & 3 \end{pmatrix}, | ||
| + | Q_2 = \begin{pmatrix} 2 & 1\\ 3 & 3 \end{pmatrix}, | ||
| + | Q_3 = \begin{pmatrix} 4 & -1\\ -1 & 3 \end{pmatrix}. | ||
| + | \] | ||
| + | |||
| + | [[Файл:Sum1.png|center|Сумма эллипсоидов]] | ||
| + | [[Файл:Ext1.png|600px|left|Внешняя аппроксимация]] | ||
| + | [[Файл:Int1.png|600px|right|Внутренняя аппроксимация]] | ||
Текущая версия на 10:42, 29 декабря 2022
Данная глава посвящена рассмотрению суммы двух эллипсоидов, будут выведены внутренние и внешние оценки. Здесь и далее в главе рассматриваются исключительно невырожденные эллипсоиды. \begin{gather*} \mathcal{E}_{1} = \mathcal{E} (a_1, Q_{1}); \\ \mathcal{E}_{2} = \mathcal{E} (a_2, Q_{2}). \\ \end{gather*}
Содержание
Определения
Сумма по Минковскому
Пусть даны два множества $$\mathcal{H}_1, \mathcal{H}_2 \subset \mathbb{R}^n$$, геометрической суммой (суммой по Минковскому) называется следующая сумма: \begin{equation} \mathcal{H}_1 + \mathcal{H}_2 = \bigcup_{h_1 \in \mathcal{H}_1} \bigcup_{h_2 \in \mathcal{H}_2} \{ h_1 + h_2\}. \end{equation}
Внешняя и внутренняя оценки
Пусть даны два эллипсоида $$\mathcal{E}_{1} = \mathcal{E} (a_1, Q_{1}), \mathcal{E}_{2} = \mathcal{E} (a_2, Q_{2})$$, будем рассматривать их сумму $$\mathcal{E}_{1} + \mathcal{E}_{2}$$. Внешней оценкой будем называть $$\mathcal{E}^{(+)}$$: \begin{equation} \mathcal{E}_{1} + \mathcal{E}_{2} \subseteq \mathcal{E}^{(+)}; \end{equation} Внутренней оценкой будем называть $$\mathcal{E}^{(-)}$$: \begin{equation} \mathcal{E}^{(-)} \subseteq \mathcal{E}_{1} + \mathcal{E}_{2}. \end{equation}
Внешние оценки
Леммы
Лемма 1
(a) Рассмотрим эллипсоид \( \mathcal{E} = \mathcal{E}(a_1 + a_2, Q(p)) \) для любых \( p > 0 \), тогда он оценивает сумму \(\mathcal{E}_1 + \mathcal{E}_2\) следующим образом:
\[
\mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E} (a_1 + a_2,Q(p)),
\]
для любого \(p > 0 \), если \( Q(p) = (1 + p^{-1})Q_1 + (1 + p)Q_2\), а \( Q_1, Q_2 \) конфигурационные матрицы (симметричные и невырожденные) первого и второго эллипсоидов соответственно.\[\]
(b) По данному вектору \( l \in R^n, \|l\| = 1\) выражение
\[
p =
\langle Q_1l,l \rangle^{\frac{1}{2}} \langle Q_2l,l \rangle^{-\frac{1}{2}}
\] определяет параметр \(p \in \Pi^{+}\), такой что
\[ \rho(l|\mathcal{E} (a_1 + a_2,Q(p))) = \rho(l|\mathcal{E}(a_1,Q_1) + \mathcal{E}(a_2,Q_2)).\]
И обратно, по данному параметру \(p \in \Pi^{+}\), существует вектор \( l \in R^n, \|l\| = 1\), удовлетворяющий вышеуказанным равенствам.
Обратим внимание, что \( \Pi^{+} = \left[ \lambda_{min}^{1/2}, \lambda_{max}^{1/2} \right] \),где \[\ \lambda_{min} = \lambda_{1} \leq \lambda_{2} \leq ... \leq \lambda_{n} = \lambda_{max}, \] корни уравнения \[ det(Q_1 - \lambda Q_2) = 0 .\]
Лемма 2
Пусть \( C \) положительно определенная симметричная матрица с элементами \( {c_{ij}} \).
Зафиксируем вектор \( l \in R^n, \|l\| = 1\) и предположим, что для некоторого \( m \in [0,n]\) имеем
\[
l_j = 0,\text{ }если\text{ }j \in \overline{1,m};\\
l_j \neq 0,\text{ }если\text{ } j = \overline{m+1,n}.
\]
Помимо этого будем считать, что $$\mathcal{E}_1 = \mathcal{E}(0,Q_1), \mathcal{E}_2 = \mathcal{E}(0,Q_2)$$, а матрицы \(Q_1, Q_2, Q\) диагональные. Если верно следующее:
\[
\mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}(0, Q),
\]
а также \[\rho(l|\mathcal{E}(0, Q)) = \rho(l|\mathcal{E}_1 + \mathcal{E}_2) .\]
Тогда
\[
c_{ij} = 0, \text{ для всех } i \neq j,\text{ } i \in \overline{m+1,n}.
\]
Лемма 3
Возьмем эллипсоид \(\mathcal{E}(0, C)\) вместе с \(\mathcal{E}_1 = \mathcal{E}(0,Q_1), \mathcal{E}_2 = \mathcal{E}(0,Q_2),\) предполагая \(Q_1 \text{ и } Q_2 \) диагональными. Также считаем данным вектор \( l \in R^n, \|l\| = 1\), параметр \(p\) считается известным ввиду Леммы 1. Тогда: \[ \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}(0, Q(p)) \] и \[ \rho(l|\mathcal{E}(0, Q(p))) = \rho(l|\mathcal{E}_1 + \mathcal{E}_2), \] тогда \[ \mathcal{E}(0,Q(p)) = \mathcal{E}(0, C)\text{ и }p\in\Pi^{+} . \]
Теоремы
Теорема 1
Предполагая, что \(\mathcal{E}_1 = \mathcal{E}(a_1,Q_1), \mathcal{E}_2 = \mathcal{E}(a_2,Q_2),\) предполагая \(Q_1 \text{ и } Q_2 \) положительно определенными, а также \(Q(p)\) определенным в соответствии с Леммой 1.
Тогда минимальное по включению множество, оценивающее сумму \( \mathcal{E}_1 + \mathcal{E}_2\), состоит из эллипсоидов вида \( \mathcal{E}(a_1 + a_2, Q(p)), где \text{ }p\in\Pi^{+}.\)
Доказательство
Не ограничивая общности, ссылаясь на Лемму из первого раздела, мы можем предложить, что все центры эллипсоидов находятся в нуле, т.е.\(a_1 = a_2 = 0\).
Пусть есть такой эллипсоид, что \( \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q)\).Давайте найдем параметр \(p\), такой, чтобы эллипсоид \(\mathcal{E}(0, Q(p))\) был зажат между \(\mathcal{E}(0, Q)\) и \( \mathcal{E}_1 + \mathcal{E}_2 \). Итого мы имеем
\[
\mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q(p)) \subseteq \mathcal{E}(0, Q).
\]
Мы можем считать, что \(\mathcal{E}(0, Q)\) касательно к \(\mathcal{E}_1 + \mathcal{E}_2\), предполагая существование вектора \( l = \overline l \in R^n, \|\overline l\| = 1\), такое, что
\[
\rho(\overline l|\mathcal{E}(0, Q)) = \rho(\overline l|\mathcal{E}_1 + \mathcal{E}_2).
\]
Давайте теперь выберем обратимую матрицу T такую, чтобы матрицы \( Q^{*}_1 = T'Q^{*}_1T ,Q^{*}_2 = T'Q^{*}_2T\) были бы обе диагональными. Существование подобной трансформационной матрицы T следует из результатов Линейной Алгебры и теории матриц.
Преобразование T не будет нарушать следующего соотношения: \( \mathcal{E}_1 + \mathcal{E}_2 \subseteq \mathcal{E}(0, Q^{*})\), таким образом с конфигурационной матрицей \( Q^{*} = T'QT\) будет справедливо следующее
\[
\mathcal{E}(0, Q^{*}_1) + \mathcal{E}(0, Q^{*}_2) \subseteq \mathcal{E}(0, Q^{*}) .
\]
Пользуясь отображением \( l = T z \) можно преобразовать тождество
\[
(\overline l, Q \overline l)^{\frac{1}{2}} = (\overline l, Q_1 \overline l)^{\frac{1}{2}} + (\overline l, Q_2 \overline l)^{\frac{1}{2}}
\]
к виду \[ (\overline z, Q^{*} \overline z)^{\frac{1}{2}} = (\overline z, Q^{*}_1 \overline z)^{\frac{1}{2}} + (\overline z, Q^{*}_2 \overline z)^{\frac{1}{2}}, \]
где \(\overline z = T^{-1} \overline l \) Далее можно будут справедливыми следующие преобразования:
\[ \overline p = (\overline z, Q^{*}_1 \overline z)^{\frac{1}{2}} (\overline z, Q^{*}_2 \overline z)^{-\frac{1}{2}}; \]
\[ Q^{*}(\overline p) = (1 + \overline p^{-1})Q^{*}_1 + (1 + \overline p)Q^{*}_2. \] Приходим к соотношению
\[ \mathcal{E}(0, Q^{*}_1) + \mathcal{E}(0, Q^{*}_2) \subseteq \mathcal{E}(0, Q^{*}(\overline p)); \]
\[
\rho(\overline z|\mathcal{E}(0, Q^{*}_1)) +\rho(\overline z|\mathcal{E}(0, Q^{*}_2)) = \rho(\overline z|\mathcal{E}(0, Q^{*}(\overline p)) = \rho(\overline z|\mathcal{E}(0, Q^{*}).
\]
Из Леммы 3 Существует вектор \( z^{*}\) удовлетворяющий следующему: \[ \rho(z^{*}|\mathcal{E}(0, Q^{*}(\overline p))) \gt \rho(z^{*}|\mathcal{E}(0, Q^{*})) . \]
Очевидно , что вектора \( z^{*}\) и \(\overline z \) неколлинеарны. Определим пространство Z как пространство, натянутое на данные векторы. А \(\mathcal{E}_z (0, Q) \) есть проекция эллипсоида на пространство Z.
\[ \mathcal{E}_z (0, Q^{*}) \subseteq \mathcal{E}_z (0, Q^{*}(\overline p)) ; \]
\[ \rho(\overline z|\mathcal{E}_z (0, Q^{*})) = \rho(\overline z|\mathcal{E}_z (0, Q^{*}(\overline p))) = \rho(\overline z|\mathcal{E}_z (0, Q^{*}_1) + \mathcal{E}_z (0, Q^{*})_2). \]
Из результатов Леммы 3 \( \mathcal{E}_z (0, Q^{*}) = \mathcal{E}_z (0, Q^{*}(p)) \). $$\blacksquare$$
Внутренние оценки
Пусть даны эллипсоиды $$\mathcal{E}(a_1, Q_1), \mathcal{E}(a_2, Q_2), Q_1 > 0, Q_2 > 0$$, рассмотрим матрицу $$Q[S]$$ \begin{equation} Q[S] = S^{-1}[(SQ_1S')^{\frac{1}{2}} + (SQ_2S')^{\frac{1}{2}}]^2S'^{-1}, \end{equation} и $$S \in \Sigma$$, где \begin{equation} \Sigma = \{S \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n) : S' = S, |S| \neq 0\}. \end{equation}
Леммы
Лемма 1
Эллипсоид $$\mathcal{E} = \mathcal{E}(a_1 + a_2, Q[S]) $$ является внутренним приближением суммы (по Минковскому) $$\mathcal{E}_1 + \mathcal{E}_2$$, а именно для любого $$S \in \Sigma:$$ \begin{equation} \mathcal{E}[S] = \mathcal{E}(a_1 + a_2, Q[S]) \subseteq \mathcal{E}_1 + \mathcal{E}_2. \end{equation} Для любого $$S \in \Sigma$$ существует вектор $$l:\|l\| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \begin{equation}\label{eq1} \rho(l|\mathcal{E}(a_1 + a_2, Q[S])) = \rho(l|\mathcal{E}_1) + \rho(l|\mathcal{E}_2). \end{equation} И наоборот, для любого $$l \in \mathbb{R}^n, \|l\| = 1$$, существует матрица $$S^* \in \Sigma$$: при $$S = S^*$$ выполняется равенство \eqref{eq1}.
Теоремы
Теорема 1
Рассмотрим несколько различных эллипсоидов подобного вида: $$\mathcal{E}(a_1 + a_2, Q[S]), S \in \Sigma$$, порожденных различными матрицами $$Q[S]$$, тогда множество внутренних оценок максимального включения суммы эллипсоидов $$\mathcal{E}_1 + \mathcal{E}_2$$ состоит из эллипсоидов вида $$\mathcal{E}(a_1 + a_2, Q[S]), S \in \Sigma$$.
Доказательство
Как и в теореме о внешних оценках предположим, что $$a_1 = a_2 = 0.$$
Для того, чтобы доказать максимальность $$\mathcal{E}(0, Q[S])$$, мы должны показать, что для любого эллипсоида $$\mathcal{E}(0, Q)$$ из того, что $$\mathcal{E}(0, Q[S]) \subseteq \mathcal{E}(0, Q) \subseteq \mathcal{E}_1 + \mathcal{E}_2$$ следует, что $$Q[S] = Q.$$
Согласно Лемме 1 о внутренних оценках существует вектор $$l:\|l\| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \eqref{eq1}.
Пусть $$z = Q_2^{-\frac{1}{2}}l^*.$$ Существует такая обратимая матрица $$B \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n)$$, которая отображает $$i$$-ый единичный вектор $$e_i \in \mathbb{R}^n$$ в $$Q_2^{-\frac{1}{2}}z_i \in \mathbb{R}^n$$, для любых $$i = 1, ..., n.$$ Это приводит к \begin{equation}\label{eq2} \rho(l, \mathcal{E}(0, B'Q[S]B)) \leq \rho(l, \mathcal{E}(0, B'QB)) \leq \rho(l, B'\mathcal{E}_1) + \rho(l, B'\mathcal{E}_2), \end{equation} для любых $$l \in \mathbb{R}^n$$. Это означает, что диагональные элементы $$B'Q[S]B$$ и $$B'QB$$ совпадают.
Подставляя $$l = e_i + e_j, i \neq j, $$ получим \begin{equation} q_{ii}^{(+)} + 2q_{ij}^{(+)} + q_{jj}^{(+)} \leq q_{ii} + 2q_{ij} + q_{jj}, \end{equation} для произвольных фиксированных $$i$$ и $$j$$, где $$q_{kr}^{(+)}$$ и $$q_{kr}$$ обозначают элементы в $$k$$-ом ряду и $$r$$-ом столбце матриц $$B'Q[S]B$$ и $$B'QB$$ соответственно. Т.к. диагональные элементы равны, получим: $$q_{ij}^{(+)} \leq q_{ij}$$.
Подставляя $$l = e_i - e_j $$ в \eqref{eq2} приходим к обратному неравенству. Следовательно, $$B'Q[S]B = B'QB$$ и благодаря обратимости $$B$$, получаем, что $$Q[S] = Q.$$ $$\blacksquare$$
Примеры
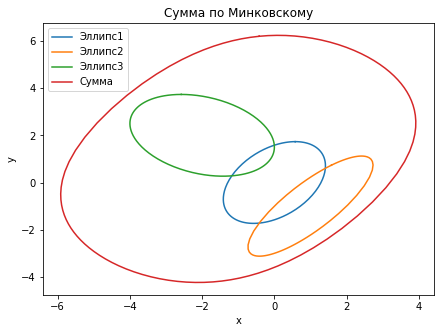
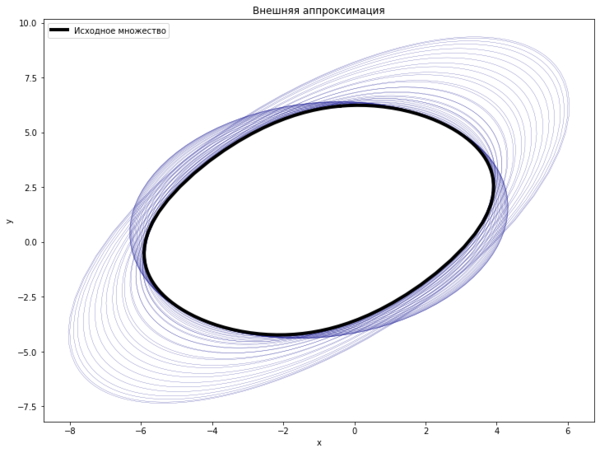
Пример 1
\[
a_1 = (3, 2), a_2 = (1, -1),
\]
\[
Q_1 = \begin{pmatrix} 2 & 3\\ 2 & 7 \end{pmatrix},
Q_2 = \begin{pmatrix} 3 & 2\\ 2 & 2 \end{pmatrix}.
\]
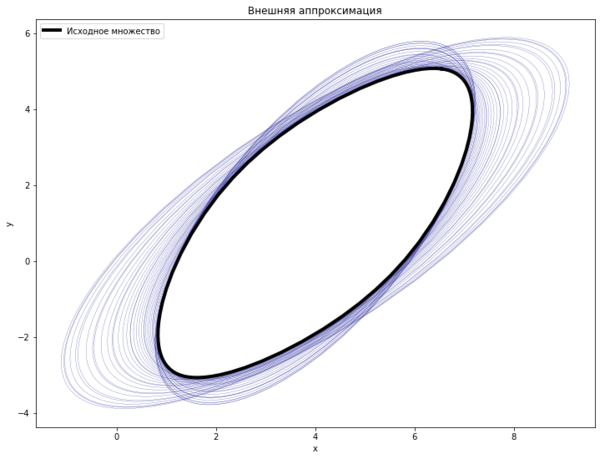
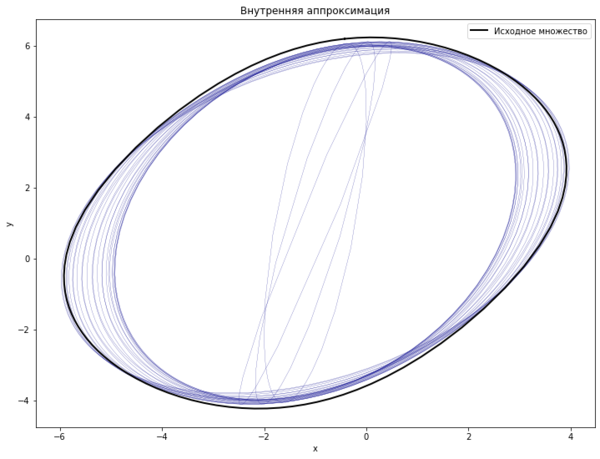
Пример 2
\[
a_1 = (0, 0), a_2 = (1, -1), a_3 = (-2, 2),
\]
\[
Q_1 = \begin{pmatrix} 2 & 1\\ 1 & 3 \end{pmatrix},
Q_2 = \begin{pmatrix} 2 & 1\\ 3 & 3 \end{pmatrix},
Q_3 = \begin{pmatrix} 4 & -1\\ -1 & 3 \end{pmatrix}.
\]