Геометрическая разность двух эллипсоидов. Внутренние и внешние оценки: различия между версиями
Ulyana (обсуждение | вклад) |
|||
| (не показано 39 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
В этой статье будут рассмотрены геометрическая разность двух эллипсоидов и ее внутренние и внешние оценки. | В этой статье будут рассмотрены геометрическая разность двух эллипсоидов и ее внутренние и внешние оценки. | ||
| − | == | + | == Основные понятия == |
| − | Разностью двух эллипсоидов будем называть $$\ | + | |
| + | Пусть $$ q \in \mathbb{R}^{n}, Q \in \mathbb{R}^{n \times n} $$ и $$Q$$ неотрицательно определена. Эллипсоидом $$\varepsilon (q, Q) $$ с центром q и матрицей Q называется выпуклое замкнутое множество точек $$\mathcal{R}^{n}$$, опорная функция $$\rho (l | \varepsilon (q, Q)$$ которого равна $$\langle l, q \rangle + \langle l, Ql \rangle^{\frac{1}{2}}$$. | ||
| + | |||
| + | В случае, когда центр $$q$$ не упоминается будем считать, что он находится в центре координат.<br> | ||
| + | |||
| + | Разностью двух эллипсоидов будем называть $$\mathcal{E}_{1} \dot{—} \mathcal{E}_{2}$$ | ||
\begin{gather*} | \begin{gather*} | ||
| − | \rho (l | \ | + | \rho (l | \mathcal{E}_{1} \dot{—} \mathcal{E}_{2}) = conv( \rho(l | \mathcal{E}_{1}) - \rho (l | \mathcal{E}_{2} )) |
\end{gather*} | \end{gather*} | ||
| + | == Внутренние эллипсоидальные оценки == | ||
| + | Пусть $$Q_{2}$$ - положительно определена, а $$Q_{1}$$ - неотрицательно определенная матрицы. Для оценивания разности эллипсоидов $$\mathcal{E} (q_{2}, Q_{2}) \dot{—} \mathcal{E} (q_{21}, Q_{1})$$ введем некоторые обозначения. Введем семейство параметрических матриц | ||
| + | \begin{gather} | ||
| + | Q(p) = (1-p)Q_{2} - (1 - \frac{1}{p})Q_{1}. | ||
| + | \end{gather} | ||
| + | Также рассмотрим уравнение | ||
| + | \begin{gather} | ||
| + | det (Q_{2} - \lambda Q_{1}) = 0 | ||
| + | \end{gather} | ||
| + | и обозначим корни этого уравнения | ||
| + | \begin{gather} | ||
| + | \lambda_{min} = \lambda_{1} \leqslant \lambda_{2} \leqslant \ldots \leqslant \lambda_{n} = \lambda_{max}, (\lambda_{1} > 0, lambda_{n} < \infty). | ||
| + | \end{gather} | ||
| + | Также обозначим | ||
| + | \begin{gather} | ||
| + | Pi^{+} = \left[ \lambda_{min}^{1/2}, \lambda_{max}^{1/2} \right], \\ | ||
| + | Pi^{-} = Pi^{+} \cap (1, \lambda_{min}). | ||
| + | \end{gather} | ||
| + | '''Лемма 1''' | ||
| + | Пусть $$\mathcal{E} (Q_{1}) \subseteq \mathcal{E} (Q_{2})$$, тогда справедливы следующие утверждения: | ||
| − | == | + | * Эллипcоид $$\mathcal{E} (q_{2} - q_{1}, Q(p))$$ невырожденный тогда и только тогда, когда $$p \in (1, \lambda_{min})$$. Для таких $$p$$ эллипсоид является внутренней аппроксимацией разности $$\mathcal{E} (q_{2} - q_{1}, Q(p)) \subseteq \mathcal{E} (Q_{1}) \dot{-} \mathcal{E} (Q_{2})$$ |
| − | + | ||
| + | * Для фиксированного вектора $$l \in \mathbb{R}^{n}, ||l|| = 1$$ выражение | ||
| + | \begin{gather} | ||
| + | p = \langle l, Q_{1}l \rangle^{\frac{1}{2}} \langle l, Q_{2}l \rangle^{-\frac{1}{2}} | ||
| + | \end{gather} | ||
| + | определяет параметр $$p$$. Если параметр $$p \in Pi^{-}$$, то | ||
| + | \begin{gather} | ||
| + | \rho(l|\mathcal{E} (q_{1} + q_{2},Q(p))) = \rho(l|\mathcal{E} (q_{1},Q_{1}) + \mathcal{E} (q_{2},Q_{2})). | ||
| + | \end{gather} | ||
| + | Также верно обратное: при заданном параметре $$p \in Pi^{-}$$ существует вектор $$l \in \mathbb{R}^{n}, ||l|| = 1$$ который обеспечивает верность равенств. | ||
| + | |||
| + | '''Лемма 2''' | ||
| + | Пусть C положительно определенная симметричная матрица с элементами \( {c_{ij}} \). | ||
| + | Для фиксированного вектора $$l \in \mathbb{R}^{n}, ||l|| = 1$$ и предположим, что для некоторого $$m \in [0,n]$$ имеем | ||
| + | \begin{gather} | ||
| + | l_j = 0,\text{ }если\text{ } j \in \overline{1,m};\\ | ||
| + | l_j \neq 0,\text{ }если\text{ } j = \overline{m+1,n}. | ||
| + | \end{gather} | ||
| + | Помимо этого будем считать, что $$\mathcal{E}_{1} = \mathcal{E}(0,Q_{1}), \mathcal{E}_{2} = \mathcal{E}(0,Q_{2})$$, а матрицы $$Q_{1}, Q_{2}, Q$$ диагональные. Если выполнено: | ||
| + | \begin{gather} | ||
| + | \mathcal{E}(0, Q) \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}, | ||
| + | \end{gather} | ||
| + | и | ||
| + | \begin{gather} | ||
| + | \rho(l|\mathcal{E}(0, Q)) = \rho(l|\mathcal{E}_{1} \cdot{-} \mathcal{E}_{2}). | ||
| + | \end{gather} | ||
| + | Тогда | ||
| + | \begin{gather} | ||
| + | c_{ij} = 0, \text{ для всех } i \neq j,\text{ } i \in \overline{m+1,n}. | ||
| + | \end{gather} | ||
| + | |||
| + | '''Лемма 3''' | ||
| + | |||
| + | Считаем эллипсоиды $$\mathcal{E}(0, C), \mathcal{E}_{1} = \mathcal{E}(0,Q_{1}), \mathcal{E}_{2} = \mathcal{E}(0,Q_{2})$$ невырожденными, а матрицы $$Q_{1}$$ и $$Q_{2}$$ диагональными. Также пусть задан вектор $$l \in \mathbb{R}^{n}, ||l|| = 1$$, параметр $$p$$ считается известным ввиду Леммы 1. В таком случае если эллипсоид корректно определен, тогда из следующих утверждений: | ||
| + | \begin{gather} | ||
| + | \mathcal{E}(0, Q(-p)) \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} | ||
| + | \end{gather} | ||
| + | и | ||
| + | \begin{gather} | ||
| + | \rho(l|\mathcal{E}(0, Q(-p))) = \rho(l|\mathcal{E}_1 \dot{-} \mathcal{E}_2), | ||
| + | \end{gather} | ||
| + | следует | ||
| + | \begin{gather} | ||
| + | \mathcal{E}(0,Q(p)) = \mathcal{E}(0, C)\text{ и }p\in\Pi^{+} . | ||
| + | \end{gather} | ||
| + | |||
| + | |||
| + | '''Теорема 1''' | ||
| + | Предполагая, что $$\mathcal{E}_{2} = \mathcal{E}(q_{2}, Q_{2})\in int \mathcal{E}_{1} = \mathcal{E}(q_{1}, Q_{1})$$. | ||
| + | Тогда максимальное по включению множество, оценивающее разность $$ \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, состоит из эллипсоидов вида | ||
| + | \begin{gather} | ||
| + | \mathcal{E}(q_{1} - q_{2}, Q(-p)), p \in \Pi^{-}. | ||
| + | \end{gather} | ||
| + | |||
| + | '''Доказательство''' | ||
| + | Не ограничивая общности, ссылаясь на Лемму из первого раздела, мы можем предложить, что все центры эллипсоидов находятся в нуле, т.е.$$q_{1} = q_{2} = 0$$. <br> | ||
| + | Пусть есть такой эллипсоид, что $$ \mathcal{E}(0, Q) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$.Найдем такой параметр $$p$$, что для эллипсоида $$\mathcal{E}(0, Q(-p))$$ будет выполнено: | ||
| + | \begin{gather} | ||
| + | \mathcal{E}(0, Q) \subseteq \mathcal{E}(0, Q(-p)) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}. | ||
| + | \end{gather} | ||
| + | Мы можем считать, что $$\mathcal{E}(0, Q)$$ касательно к $$mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, и что будет существовать вектор $$l = \overline{l} \in \mathbb{R}^{n}, ||\overline {l}|| = 1$$, такой, что | ||
| + | \begin{gather}\label{eq1} | ||
| + | \rho(\overline l|\mathcal{E}(0, Q)) = \rho(\overline l|\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}). | ||
| + | \end{gather} | ||
| + | Возьмем $$\mathcal{E}(0, Q(- \overline{p}))$$, где | ||
| + | \begin{gather} | ||
| + | \overline{p} = \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}} \langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} | ||
| + | \end{gather} | ||
| + | и докажем, что матрица $$\mathcal{E}(0, Q(- \overline{p}))$$ положительно определенная. Для этого определим матрицу | ||
| + | \begin{gather*} | ||
| + | D(p^{*}) = (1 + (p^{*})^{-1})Q + (1 + p^{*})Q_{2} | ||
| + | \end{gather*} | ||
| + | или | ||
| + | \begin{gather}\label{eq2} | ||
| + | Q = (1 - p^{-1})D(p^{*}) + (1 - p)Q_{2} | ||
| + | \end{gather} | ||
| + | где | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | p^{*} = \langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} \langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} | |
| − | |||
| − | |||
\end{gather*} | \end{gather*} | ||
| − | + | и | |
\begin{gather*} | \begin{gather*} | ||
| − | + | p = p^{*} + 1. | |
| − | |||
| − | |||
| − | |||
\end{gather*} | \end{gather*} | ||
| − | + | Из [https://sawiki.cs.msu.ru//index.php/Сумма_двух_эллипсоидов._Внутренние_и_внешние_оценки Теоремы 1] мы получаем | |
\begin{gather*} | \begin{gather*} | ||
| − | + | \mathcal{E} (0, Q) + \mathcal{E}_{2} \subseteq \mathcal{E} (0, D(p^{*})) \subseteq \mathcal{E}_{1} | |
| − | + | \end{gather*} | |
| − | \end{gather | + | или иначе $$ D(p^{*}) \leqslant Q_{1}$$. Более того, |
| − | + | \begin{gather} | |
| + | \rho(\overline l|\mathcal{E}(0, D(p^{*}))) = \rho(\overline l|\mathcal{E}(0, Q)) + \rho(\overline l|\mathcal{E}(0, Q_{2})). | ||
| + | \end{gather} | ||
| + | Из \ref{eq1} получаем | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | \rho(\overline l|\mathcal{E}(0, Q)) + \rho(\overline l|\mathcal{E}_{2}) \leqslant \rho(\overline l|\mathcal{E}_{1}) | |
| − | |||
| − | |||
| − | |||
\end{gather*} | \end{gather*} | ||
| − | + | или | |
\begin{gather*} | \begin{gather*} | ||
| − | + | \langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} + \langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} \leqslant \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}}, | |
\end{gather*} | \end{gather*} | ||
| − | + | так что | |
| − | + | \begin{gather*} | |
| − | + | p = p^{*} + 1 = ( \langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} + \langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} )\langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} = | |
| + | ( \langle \overline{l}, D(p^{*})\overline{l} \rangle^{\frac{1}{2}})\langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} \leqslant ( \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}})\langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} = \overline{p}. | ||
| + | \end{gather*} | ||
| + | Вместе с \ref{eq2} и неравенством $$ p \leqslant \overline{p}$$ это позволяет заключить, что $$Q \leqslant Q(- \overline{p})$$, что также доказывает, что $$Q(- \overline{p}) > 0$$, что означает, что $$\overline{p} \in (1, \lambda_{min})$$/. С другой стороны, в силу Леммы 1 мы имеем $$ \mathcal{E}(0, Q(- \overline{p})) \in \mathcal{E}(0, Q_{1}) \dot{-} \mathcal{E}(0, Q_{2}) $$/. Отсюда получаем желаемый результат. | ||
| + | |||
| + | == Внешние эллипсоидальные оценки == | ||
| + | Пусть даны эллипсоиды $$\mathcal{E}(q_1, Q_1), \mathcal{E}(q_2, Q_2), Q_1 > 0, Q_2 > 0$$, рассмотрим матрицу $$Q_{-}[S]$$ | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | Q_{-}[S] = S^{-1}[(SQ_1S')^{\frac{1}{2}} - (SQ_2S')^{\frac{1}{2}}]^2S'^{-1}, | |
| − | |||
| − | |||
| − | |||
\end{gather*} | \end{gather*} | ||
| − | + | и $$S \in \Sigma$$, где | |
\begin{gather*} | \begin{gather*} | ||
| − | + | \Sigma = \{S \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n) : S' = S, |S| \neq 0\}. | |
| − | + | \end{gather*} | |
| − | + | '''Лемма 4''' | |
| + | Эллипсоид $$\mathcal{E} = \mathcal{E}(q_{1} +- q_{2}, Q_{-}[S]) $$ является внешним приближением геометрической разности (по Минковскому) $$\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, а именно для любого $$S \in \Sigma:$$ | ||
| + | \begin{gather*} | ||
| + | \mathcal{E}_1 \dot{-} \mathcal{E}_2 \subseteq \mathcal{E}[S] = \mathcal{E}(q_{1} - q_{2}, Q_{-}[S]). | ||
\end{gather*} | \end{gather*} | ||
| − | + | Для любого $$S \in \Sigma$$ существует вектор $$l||l|| = 1$$, такой, что при $$l = l^*$$ выполняется равенство | |
| + | \begin{equation}\label{eq3} | ||
| + | \rho(l|\mathcal{E}(q_{1} - q_{2}, Q_{-}[S])) = \rho(l|\mathcal{E}_{1}) \dot{-} \rho(l|\mathcal{E}_{2}). | ||
| + | \end{equation} | ||
| + | И наоборот, для любого $$l \in \mathbb{R}^n, \|l\| = 1$$, существует матрица $$S^* \in \Sigma$$: при $$S = S^*$$ выполняется равенство \ref{eq3}. | ||
| + | |||
| + | '''Теорема 2''' | ||
| + | Рассмотрим различные эллипсоиды вида: $$\mathcal{E}(q_{1} - q_{2}, Q_{-}[S]), S \in \Sigma$$, которые получаются с помощью различных матриц $$Q_{-}[S]$$, тогда, предполагая $$\mathcal{E}_{2} \subseteq \mathcal{E}_{1}$$ множество внешних оценок минимального включения геометрической разности эллипсоидов $$\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$ состоит из эллипсоидов вида $$\mathcal{E}(q_{1} - q_{2}, Q_{-}[S]), S \in \Sigma$$. | ||
| + | |||
| + | '''Доказательство'''<br> | ||
| + | |||
| + | Как и в теореме о внешних оценках предположим, что $$q_{1}= q_{2} = 0.$$ | ||
| + | |||
| + | Для того, чтобы доказать минимальность $$\mathcal{E}(0, Q[S])$$, мы должны показать, что для любого эллипсоида $$\mathcal{E}(0, Q)$$ из того, что $$ \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} \subseteq \mathcal{E}(0, Q) \subseteq \mathcal{E}(0, Q_{-}[S])$$ следует, что $$Q_{-}[S] = Q$$. | ||
| + | |||
| + | Согласно Лемме 4 существует вектор $$l:||l|| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \ref{eq3}. | ||
| + | |||
| + | Пусть $$z = Q_{2}^{-\frac{1}{2}}l^*.$$ Существует такая обратимая матрица $$B \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n)$$, которая отображает $$i$$-ый единичный вектор $$e_{i} \in \mathbb{R}^{n}$$ в $$Q_{2}^{-\frac{1}{2}}z_{i} \in \mathbb{R}^{n}$$, для любых $$i = 1, ..., n.$$ Это приводит к | ||
| + | \begin{gather}\label{eq4} | ||
| + | \rho(l, B'\mathcal{E}_{1}) \dot{-} \rho(l, B'\mathcal{E}_{2}) \leq \rho(l, \mathcal{E}(0, B'QB)) \leq \rho(l, \mathcal{E}(0, B'Q_{-}[S]B)), | ||
| + | \end{gather} | ||
| + | для любых $$l \in \mathbb{R}^{n}$$. Это означает, что диагональные элементы $$B'Q_{-}[S]B$$ и $$B'QB$$ совпадают. | ||
| + | |||
| + | Подставляя $$l = e_{i} + e_{j}, i \neq j, $$ получим | ||
| + | \begin{equation} | ||
| + | q_{ii}^{(+)} + 2q_{ij}^{(+)} + q_{jj}^{(+)} \leq q_{ii} + 2q_{ij} + q_{jj}, | ||
| + | \end{equation} | ||
| + | для произвольных фиксированных $$i$$ и $$j$$, где $$q_{kr}^{(+)}$$ и $$q_{kr}$$ обозначают элементы в $$k$$-ом ряду и $$r$$-ом столбце матриц $$B'Q_{-}[S]B$$ и $$B'QB$$ соответственно. Т.к. диагональные элементы равны, получим: $$q_{ij}^{(+)} \leq q_{ij}$$. | ||
| + | |||
| + | Подставляя $$l = e_{i} - e_{j} $$ в \ref{eq4} приходим к обратному неравенству. Следовательно, $$B'Q_{-}[S]B = B'QB$$ и благодаря обратимости $$B$$, получаем, что $$Q_{-}[S] = Q$$. Из доказательства теоремы следует утверждение:<br> | ||
| + | |||
| + | '''Утверждение''' Следующее равенство верно: | ||
| + | \begin{gather} | ||
| + | \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} = \cap \{ \mathcal{E}(q_{1} - q_{2}, Q_{-}[S]) | S \in \Sigma. \}. | ||
| + | \end{gather} | ||
| − | == | + | == Примеры == |
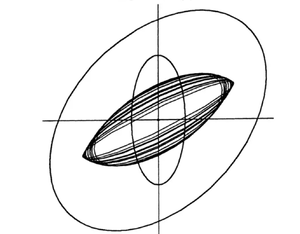
| + | '''Внутренняя оценка''' | ||
| + | [[Файл:Внутренняя оценка тру.png|center|мини]] | ||
| + | <br> | ||
| + | <br> | ||
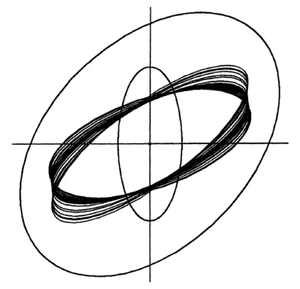
| + | '''Внешняя оценка''' | ||
| + | [[Файл:Внутренняя оценка.png|center|мини]] | ||
Текущая версия на 06:16, 3 марта 2023
В этой статье будут рассмотрены геометрическая разность двух эллипсоидов и ее внутренние и внешние оценки.
Содержание
Основные понятия
Пусть $$ q \in \mathbb{R}^{n}, Q \in \mathbb{R}^{n \times n} $$ и $$Q$$ неотрицательно определена. Эллипсоидом $$\varepsilon (q, Q) $$ с центром q и матрицей Q называется выпуклое замкнутое множество точек $$\mathcal{R}^{n}$$, опорная функция $$\rho (l | \varepsilon (q, Q)$$ которого равна $$\langle l, q \rangle + \langle l, Ql \rangle^{\frac{1}{2}}$$.
В случае, когда центр $$q$$ не упоминается будем считать, что он находится в центре координат.
Разностью двух эллипсоидов будем называть $$\mathcal{E}_{1} \dot{—} \mathcal{E}_{2}$$ \begin{gather*} \rho (l | \mathcal{E}_{1} \dot{—} \mathcal{E}_{2}) = conv( \rho(l | \mathcal{E}_{1}) - \rho (l | \mathcal{E}_{2} )) \end{gather*}
Внутренние эллипсоидальные оценки
Пусть $$Q_{2}$$ - положительно определена, а $$Q_{1}$$ - неотрицательно определенная матрицы. Для оценивания разности эллипсоидов $$\mathcal{E} (q_{2}, Q_{2}) \dot{—} \mathcal{E} (q_{21}, Q_{1})$$ введем некоторые обозначения. Введем семейство параметрических матриц \begin{gather} Q(p) = (1-p)Q_{2} - (1 - \frac{1}{p})Q_{1}. \end{gather} Также рассмотрим уравнение \begin{gather} det (Q_{2} - \lambda Q_{1}) = 0 \end{gather} и обозначим корни этого уравнения \begin{gather} \lambda_{min} = \lambda_{1} \leqslant \lambda_{2} \leqslant \ldots \leqslant \lambda_{n} = \lambda_{max}, (\lambda_{1} > 0, lambda_{n} < \infty). \end{gather} Также обозначим \begin{gather} Pi^{+} = \left[ \lambda_{min}^{1/2}, \lambda_{max}^{1/2} \right], \\ Pi^{-} = Pi^{+} \cap (1, \lambda_{min}). \end{gather} Лемма 1 Пусть $$\mathcal{E} (Q_{1}) \subseteq \mathcal{E} (Q_{2})$$, тогда справедливы следующие утверждения:
- Эллипcоид $$\mathcal{E} (q_{2} - q_{1}, Q(p))$$ невырожденный тогда и только тогда, когда $$p \in (1, \lambda_{min})$$. Для таких $$p$$ эллипсоид является внутренней аппроксимацией разности $$\mathcal{E} (q_{2} - q_{1}, Q(p)) \subseteq \mathcal{E} (Q_{1}) \dot{-} \mathcal{E} (Q_{2})$$
- Для фиксированного вектора $$l \in \mathbb{R}^{n}, ||l|| = 1$$ выражение
\begin{gather} p = \langle l, Q_{1}l \rangle^{\frac{1}{2}} \langle l, Q_{2}l \rangle^{-\frac{1}{2}} \end{gather} определяет параметр $$p$$. Если параметр $$p \in Pi^{-}$$, то \begin{gather} \rho(l|\mathcal{E} (q_{1} + q_{2},Q(p))) = \rho(l|\mathcal{E} (q_{1},Q_{1}) + \mathcal{E} (q_{2},Q_{2})). \end{gather} Также верно обратное: при заданном параметре $$p \in Pi^{-}$$ существует вектор $$l \in \mathbb{R}^{n}, ||l|| = 1$$ который обеспечивает верность равенств.
Лемма 2 Пусть C положительно определенная симметричная матрица с элементами \( {c_{ij}} \). Для фиксированного вектора $$l \in \mathbb{R}^{n}, ||l|| = 1$$ и предположим, что для некоторого $$m \in [0,n]$$ имеем \begin{gather} l_j = 0,\text{ }если\text{ } j \in \overline{1,m};\\ l_j \neq 0,\text{ }если\text{ } j = \overline{m+1,n}. \end{gather} Помимо этого будем считать, что $$\mathcal{E}_{1} = \mathcal{E}(0,Q_{1}), \mathcal{E}_{2} = \mathcal{E}(0,Q_{2})$$, а матрицы $$Q_{1}, Q_{2}, Q$$ диагональные. Если выполнено: \begin{gather} \mathcal{E}(0, Q) \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}, \end{gather} и \begin{gather} \rho(l|\mathcal{E}(0, Q)) = \rho(l|\mathcal{E}_{1} \cdot{-} \mathcal{E}_{2}). \end{gather} Тогда \begin{gather} c_{ij} = 0, \text{ для всех } i \neq j,\text{ } i \in \overline{m+1,n}. \end{gather}
Лемма 3
Считаем эллипсоиды $$\mathcal{E}(0, C), \mathcal{E}_{1} = \mathcal{E}(0,Q_{1}), \mathcal{E}_{2} = \mathcal{E}(0,Q_{2})$$ невырожденными, а матрицы $$Q_{1}$$ и $$Q_{2}$$ диагональными. Также пусть задан вектор $$l \in \mathbb{R}^{n}, ||l|| = 1$$, параметр $$p$$ считается известным ввиду Леммы 1. В таком случае если эллипсоид корректно определен, тогда из следующих утверждений: \begin{gather} \mathcal{E}(0, Q(-p)) \subseteq \mathcal{E}(0, C) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} \end{gather} и \begin{gather} \rho(l|\mathcal{E}(0, Q(-p))) = \rho(l|\mathcal{E}_1 \dot{-} \mathcal{E}_2), \end{gather} следует \begin{gather} \mathcal{E}(0,Q(p)) = \mathcal{E}(0, C)\text{ и }p\in\Pi^{+} . \end{gather}
Теорема 1
Предполагая, что $$\mathcal{E}_{2} = \mathcal{E}(q_{2}, Q_{2})\in int \mathcal{E}_{1} = \mathcal{E}(q_{1}, Q_{1})$$.
Тогда максимальное по включению множество, оценивающее разность $$ \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, состоит из эллипсоидов вида
\begin{gather}
\mathcal{E}(q_{1} - q_{2}, Q(-p)), p \in \Pi^{-}.
\end{gather}
Доказательство
Не ограничивая общности, ссылаясь на Лемму из первого раздела, мы можем предложить, что все центры эллипсоидов находятся в нуле, т.е.$$q_{1} = q_{2} = 0$$.
Пусть есть такой эллипсоид, что $$ \mathcal{E}(0, Q) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$.Найдем такой параметр $$p$$, что для эллипсоида $$\mathcal{E}(0, Q(-p))$$ будет выполнено:
\begin{gather}
\mathcal{E}(0, Q) \subseteq \mathcal{E}(0, Q(-p)) \subseteq \mathcal{E}_{1} \dot{-} \mathcal{E}_{2}.
\end{gather}
Мы можем считать, что $$\mathcal{E}(0, Q)$$ касательно к $$mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, и что будет существовать вектор $$l = \overline{l} \in \mathbb{R}^{n}, ||\overline {l}|| = 1$$, такой, что
\begin{gather}\label{eq1}
\rho(\overline l|\mathcal{E}(0, Q)) = \rho(\overline l|\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}).
\end{gather}
Возьмем $$\mathcal{E}(0, Q(- \overline{p}))$$, где
\begin{gather}
\overline{p} = \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}} \langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}}
\end{gather}
и докажем, что матрица $$\mathcal{E}(0, Q(- \overline{p}))$$ положительно определенная. Для этого определим матрицу
\begin{gather*}
D(p^{*}) = (1 + (p^{*})^{-1})Q + (1 + p^{*})Q_{2}
\end{gather*}
или
\begin{gather}\label{eq2}
Q = (1 - p^{-1})D(p^{*}) + (1 - p)Q_{2}
\end{gather}
где
\begin{gather*}
p^{*} = \langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} \langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}}
\end{gather*}
и
\begin{gather*}
p = p^{*} + 1.
\end{gather*}
Из Теоремы 1 мы получаем
\begin{gather*}
\mathcal{E} (0, Q) + \mathcal{E}_{2} \subseteq \mathcal{E} (0, D(p^{*})) \subseteq \mathcal{E}_{1}
\end{gather*}
или иначе $$ D(p^{*}) \leqslant Q_{1}$$. Более того,
\begin{gather}
\rho(\overline l|\mathcal{E}(0, D(p^{*}))) = \rho(\overline l|\mathcal{E}(0, Q)) + \rho(\overline l|\mathcal{E}(0, Q_{2})).
\end{gather}
Из \ref{eq1} получаем
\begin{gather*}
\rho(\overline l|\mathcal{E}(0, Q)) + \rho(\overline l|\mathcal{E}_{2}) \leqslant \rho(\overline l|\mathcal{E}_{1})
\end{gather*}
или
\begin{gather*}
\langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} + \langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} \leqslant \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}},
\end{gather*}
так что
\begin{gather*}
p = p^{*} + 1 = ( \langle \overline{l}, Q\overline{l} \rangle^{\frac{1}{2}} + \langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} )\langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} =
( \langle \overline{l}, D(p^{*})\overline{l} \rangle^{\frac{1}{2}})\langle \overline{l}, Q_{2}\overline{l} \rangle^{\frac{1}{2}} \leqslant ( \langle \overline{l}, Q_{1}\overline{l} \rangle^{\frac{1}{2}})\langle \overline{l}, Q_{2}\overline{l} \rangle^{-\frac{1}{2}} = \overline{p}.
\end{gather*}
Вместе с \ref{eq2} и неравенством $$ p \leqslant \overline{p}$$ это позволяет заключить, что $$Q \leqslant Q(- \overline{p})$$, что также доказывает, что $$Q(- \overline{p}) > 0$$, что означает, что $$\overline{p} \in (1, \lambda_{min})$$/. С другой стороны, в силу Леммы 1 мы имеем $$ \mathcal{E}(0, Q(- \overline{p})) \in \mathcal{E}(0, Q_{1}) \dot{-} \mathcal{E}(0, Q_{2}) $$/. Отсюда получаем желаемый результат.
Внешние эллипсоидальные оценки
Пусть даны эллипсоиды $$\mathcal{E}(q_1, Q_1), \mathcal{E}(q_2, Q_2), Q_1 > 0, Q_2 > 0$$, рассмотрим матрицу $$Q_{-}[S]$$ \begin{gather*} Q_{-}[S] = S^{-1}[(SQ_1S')^{\frac{1}{2}} - (SQ_2S')^{\frac{1}{2}}]^2S'^{-1}, \end{gather*} и $$S \in \Sigma$$, где \begin{gather*} \Sigma = \{S \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n) : S' = S, |S| \neq 0\}. \end{gather*} Лемма 4 Эллипсоид $$\mathcal{E} = \mathcal{E}(q_{1} +- q_{2}, Q_{-}[S]) $$ является внешним приближением геометрической разности (по Минковскому) $$\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$, а именно для любого $$S \in \Sigma:$$ \begin{gather*} \mathcal{E}_1 \dot{-} \mathcal{E}_2 \subseteq \mathcal{E}[S] = \mathcal{E}(q_{1} - q_{2}, Q_{-}[S]). \end{gather*} Для любого $$S \in \Sigma$$ существует вектор $$l||l|| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \begin{equation}\label{eq3} \rho(l|\mathcal{E}(q_{1} - q_{2}, Q_{-}[S])) = \rho(l|\mathcal{E}_{1}) \dot{-} \rho(l|\mathcal{E}_{2}). \end{equation} И наоборот, для любого $$l \in \mathbb{R}^n, \|l\| = 1$$, существует матрица $$S^* \in \Sigma$$: при $$S = S^*$$ выполняется равенство \ref{eq3}.
Теорема 2 Рассмотрим различные эллипсоиды вида: $$\mathcal{E}(q_{1} - q_{2}, Q_{-}[S]), S \in \Sigma$$, которые получаются с помощью различных матриц $$Q_{-}[S]$$, тогда, предполагая $$\mathcal{E}_{2} \subseteq \mathcal{E}_{1}$$ множество внешних оценок минимального включения геометрической разности эллипсоидов $$\mathcal{E}_{1} \dot{-} \mathcal{E}_{2}$$ состоит из эллипсоидов вида $$\mathcal{E}(q_{1} - q_{2}, Q_{-}[S]), S \in \Sigma$$.
Доказательство
Как и в теореме о внешних оценках предположим, что $$q_{1}= q_{2} = 0.$$
Для того, чтобы доказать минимальность $$\mathcal{E}(0, Q[S])$$, мы должны показать, что для любого эллипсоида $$\mathcal{E}(0, Q)$$ из того, что $$ \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} \subseteq \mathcal{E}(0, Q) \subseteq \mathcal{E}(0, Q_{-}[S])$$ следует, что $$Q_{-}[S] = Q$$.
Согласно Лемме 4 существует вектор $$l:||l|| = 1$$, такой, что при $$l = l^*$$ выполняется равенство \ref{eq3}.
Пусть $$z = Q_{2}^{-\frac{1}{2}}l^*.$$ Существует такая обратимая матрица $$B \in \mathcal{L}(\mathbb{R}^n, \mathbb{R}^n)$$, которая отображает $$i$$-ый единичный вектор $$e_{i} \in \mathbb{R}^{n}$$ в $$Q_{2}^{-\frac{1}{2}}z_{i} \in \mathbb{R}^{n}$$, для любых $$i = 1, ..., n.$$ Это приводит к \begin{gather}\label{eq4} \rho(l, B'\mathcal{E}_{1}) \dot{-} \rho(l, B'\mathcal{E}_{2}) \leq \rho(l, \mathcal{E}(0, B'QB)) \leq \rho(l, \mathcal{E}(0, B'Q_{-}[S]B)), \end{gather} для любых $$l \in \mathbb{R}^{n}$$. Это означает, что диагональные элементы $$B'Q_{-}[S]B$$ и $$B'QB$$ совпадают.
Подставляя $$l = e_{i} + e_{j}, i \neq j, $$ получим \begin{equation} q_{ii}^{(+)} + 2q_{ij}^{(+)} + q_{jj}^{(+)} \leq q_{ii} + 2q_{ij} + q_{jj}, \end{equation} для произвольных фиксированных $$i$$ и $$j$$, где $$q_{kr}^{(+)}$$ и $$q_{kr}$$ обозначают элементы в $$k$$-ом ряду и $$r$$-ом столбце матриц $$B'Q_{-}[S]B$$ и $$B'QB$$ соответственно. Т.к. диагональные элементы равны, получим: $$q_{ij}^{(+)} \leq q_{ij}$$.
Подставляя $$l = e_{i} - e_{j} $$ в \ref{eq4} приходим к обратному неравенству. Следовательно, $$B'Q_{-}[S]B = B'QB$$ и благодаря обратимости $$B$$, получаем, что $$Q_{-}[S] = Q$$. Из доказательства теоремы следует утверждение:
Утверждение Следующее равенство верно: \begin{gather} \mathcal{E}_{1} \dot{-} \mathcal{E}_{2} = \cap \{ \mathcal{E}(q_{1} - q_{2}, Q_{-}[S]) | S \in \Sigma. \}. \end{gather}
Примеры
Внутренняя оценка
Внешняя оценка