Задача быстродействия "из точки в точку": различия между версиями
Alina22 (обсуждение | вклад) |
Alina22 (обсуждение | вклад) |
||
| (не показано 9 промежуточных версий этого же участника) | |||
| Строка 19: | Строка 19: | ||
Заметим, что в общем случае функционал имеет вид: | Заметим, что в общем случае функционал имеет вид: | ||
\[ | \[ | ||
| − | \mathcal{J} = \int\limits_{t_0}^{t_1}f^0(x(t), u(t))dt \rightarrow \underset{u(\cdot)}{\text{inf}} | + | \mathcal{J} = \int\limits_{t_0}^{t_1}f^0(x(t), u(t))\,dt \rightarrow \underset{u(\cdot)}{\text{inf}} |
\] | \] | ||
Принимая \(f^0 \equiv 1 \), получаем задачу быстродействия с функционалом \(\mathcal{J} = t_1 - t_0\). | Принимая \(f^0 \equiv 1 \), получаем задачу быстродействия с функционалом \(\mathcal{J} = t_1 - t_0\). | ||
| Строка 35: | Строка 35: | ||
\] | \] | ||
| − | Заметим, что '''гамильтонианом''' системы называется \(M = \underset{u\in \mathcal{P}}{\text{sup}} \mathcal{H}(\psi, x, u)\). Однако в задаче быстродействия супремум достижим, поэтому \(M = \underset{u\in \mathcal{P}}{\text{max}} \langle \psi, f(x(t), u(t)) \rangle\). | + | Заметим, что '''гамильтонианом''' системы называется \(M = \underset{u\in \mathcal{P}}{\text{sup}} \, \mathcal{H}(\psi, x, u)\). Однако в задаче быстродействия супремум достижим, поэтому \(M = \underset{u\in \mathcal{P}}{\text{max}} \, \langle \psi, f(x(t), u(t)) \rangle\). |
== Принцип максимума Понтрягина == | == Принцип максимума Понтрягина == | ||
| Строка 73: | Строка 73: | ||
\dot{x}_1 = x_2, \\ | \dot{x}_1 = x_2, \\ | ||
\dot{x}_2 = u, \\ | \dot{x}_2 = u, \\ | ||
| − | + | x_1(0) = x_1^0, \\ | |
| − | + | x_2(0) = x_2^0, \\ | |
| + | x_1(t_1) = 0, \\ | ||
| + | x_2(t_1) = 0, \\ | ||
u \in [-1, 1]. | u \in [-1, 1]. | ||
\end{cases} | \end{cases} | ||
| Строка 95: | Строка 97: | ||
Из условия максимума имеем, что: | Из условия максимума имеем, что: | ||
\[ | \[ | ||
| − | u^*(t) = \text{sgn}(\psi_2(t)). | + | u^*(t) = \text{sgn}\, (\psi_2(t)). |
\] | \] | ||
| − | Поскольку \(\ddot{\psi}_2 = 0\), то \(\psi_2 = \alpha +\beta t \), а значит \(u^*(t) = \text{sgn}(\alpha +\beta t)\). Следовательно, \(u(t)\) кусочно постоянно, принимает только экстремальные значения \(\pm 1\) и имеет не более одного переключения (точки разрыва). | + | Поскольку \(\ddot{\psi}_2 = 0\), то \(\psi_2 = \alpha +\beta t \), а значит \(u^*(t) = \text{sgn}\, (\alpha +\beta t)\). Следовательно, \(u(t)\) кусочно постоянно, принимает только экстремальные значения \(\pm 1\) и имеет не более одного переключения (точки разрыва). |
Отыщем все траектории, соответствующие таким управлениям и приходящие в нуль. Найдем решения следующей системы: | Отыщем все траектории, соответствующие таким управлениям и приходящие в нуль. Найдем решения следующей системы: | ||
| Строка 113: | Строка 115: | ||
Из семейства функций, являющихся решением, найдем те, которые не имеют переключений: | Из семейства функций, являющихся решением, найдем те, которые не имеют переключений: | ||
\[ | \[ | ||
| − | x_1 = \frac{x_2^2}{2}, x_2 < 0, \ | + | x_1 = \frac{x_2^2}{2}, x_2 < 0, \dot{x}_2 > 0; \\ |
| − | x_1 = -\frac{x_2^2}{2}, x_2 > 0, \ | + | x_1 = -\frac{x_2^2}{2}, x_2 > 0, \dot{x}_2 < 0. |
\] | \] | ||
| Строка 131: | Строка 133: | ||
\begin{cases} | \begin{cases} | ||
\frac{x_2^2}{2} - \frac{q^2}{2} + p, x_2 < q, \dot{x}_2 > 0, \\ | \frac{x_2^2}{2} - \frac{q^2}{2} + p, x_2 < q, \dot{x}_2 > 0, \\ | ||
| − | -\frac{x_2^2}{2}, 0 < x_2 < q, \dot{ | + | -\frac{x_2^2}{2}, 0 < x_2 < q, \dot{x}_2 < 0. |
\end{cases} | \end{cases} | ||
\] | \] | ||
| Строка 138: | Строка 140: | ||
[[Файл:grafpng.png|центр|обрамить|Общий вид оптимального синтеза]] | [[Файл:grafpng.png|центр|обрамить|Общий вид оптимального синтеза]] | ||
| + | |||
| + | Поскольку через любую точку вида \((x_1, x_2)\) проходит единственная кривая из представленных, то для любой начальной точки существует единственная траектория, переводящая ей в конечную. Оптимальные траектории существуют, значит и решение оптимально. | ||
=== Пример 2 === | === Пример 2 === | ||
| Строка 171: | Строка 175: | ||
\] | \] | ||
| − | Так как \(\ddot{\psi}_2 = \psi_2\), то \(\psi_2 = \alpha\text{sin}(t+\beta), \alpha, \beta = const\). При этом \(\alpha \neq 0\), поскольку иначе \(\psi_2 = 0 \rightarrow \psi_1 = 0\) (из сопряженной системы) \(~-\) а это противоречит принципу максимума. | + | Так как \(\ddot{\psi}_2 = \psi_2\), то \(\psi_2 = \alpha\, \text{sin}(t+\beta), \alpha, \beta = const\). При этом \(\alpha \neq 0\), поскольку иначе \(\psi_2 = 0 \rightarrow \psi_1 = 0\) (из сопряженной системы) \(~-\) а это противоречит принципу максимума. |
| − | Поскольку \(u^*(t) = \text{sgn}(\alpha\text{sin}(t+\beta))\), то переключения зависят от первого момента переключения \(\tau \in [0, t]\) и изначального знака \(\text{sgn}(u^*(0)) \in \{\pm1\} \). Сами переключения будут происходить через каждое \(\pi\) от начального переключения \(\tau\). Оптимальное управление принимает только значение \(\pm 1\), тогда траектории \((x_1(t), x_2(t)\) состоят из кусков, удовлетворяющих системе: | + | Поскольку \(u^*(t) = \text{sgn}(\alpha\, \text{sin}(t+\beta))\), то переключения зависят от первого момента переключения \(\tau \in [0, t]\) и изначального знака \(\text{sgn}\, (u^*(0)) \in \{\pm1\} \). Сами переключения будут происходить через каждое \(\pi\) от начального переключения \(\tau\). Оптимальное управление принимает только значение \(\pm 1\), тогда траектории \((x_1(t), x_2(t)\) состоят из кусков, удовлетворяющих системе: |
\[ | \[ | ||
\begin{cases} | \begin{cases} | ||
| Строка 198: | Строка 202: | ||
[[Файл:graf_2.png|центр|обрамить|Оптимальные траектории]] | [[Файл:graf_2.png|центр|обрамить|Оптимальные траектории]] | ||
| + | |||
| + | Поскольку для любой точки вида \((x_1, x_2)\) существует единственная кривая из семейства выше, то можно однозначно восстановить оптимальную траекторию. | ||
== Список литературы == | == Список литературы == | ||
* Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976, | * Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976, | ||
* А.А. Аграчев, Ю.Л. Сачков. "Геометрическая теория управления". Москва, Физматлит, 2005 | * А.А. Аграчев, Ю.Л. Сачков. "Геометрическая теория управления". Москва, Физматлит, 2005 | ||
Текущая версия на 22:48, 14 февраля 2023
Содержание
Постановка задачи
Задача быстродействия\(~-\) задача перевода системы из начального фиксированного положения в конечное, также фиксированное, положение за минимальное время.
Пусть наша система описывается следующими условиями: \[ \begin{cases} \dot{x}(t) = f(x(t), u(t)), \\ x(t_0) = x^0, \\ x(t_1) = x^1, \\ u(\tau) \in \mathcal{P}(\tau) \in \text{conv} \, \mathbb{R}^m, \\ t_1 - t_0 \rightarrow \underset{u(\cdot)}{\text{inf}}, \end{cases} \]
где \(x_0, x_1, t_0 \) \(~-\) фиксированы, \(A(t), B(t), f(t) \) \(~-\) непрерывны, а \(\mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \(l: \rho(l\vert\mathcal{P}(\tau)\) по \(\tau\) непрерывна\(^1\)).
\(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P} = [a(\tau), b(\tau)]\); непрерывность многозначного отображения означает, что \(a(\tau), b(\tau)\) - непрерывны.
Заметим, что в общем случае функционал имеет вид: \[ \mathcal{J} = \int\limits_{t_0}^{t_1}f^0(x(t), u(t))\,dt \rightarrow \underset{u(\cdot)}{\text{inf}} \] Принимая \(f^0 \equiv 1 \), получаем задачу быстродействия с функционалом \(\mathcal{J} = t_1 - t_0\).
Сопряженная переменная имеет следующий вид: \(\psi = (\psi_1, ..., \psi_n)\).
Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H}(\psi, x, u) = \langle \psi, f(x(t), u(t)) \rangle. \]
Тогда можно говорить о сопряженной системе: \[ \dot{\psi} = -\frac{\partial \mathcal{H}}{\partial x(t)}. \]
Заметим, что гамильтонианом системы называется \(M = \underset{u\in \mathcal{P}}{\text{sup}} \, \mathcal{H}(\psi, x, u)\). Однако в задаче быстродействия супремум достижим, поэтому \(M = \underset{u\in \mathcal{P}}{\text{max}} \, \langle \psi, f(x(t), u(t)) \rangle\).
Принцип максимума Понтрягина
Теорема(ПМП для автономной задачи быстродействия)
Пусть \((x^*(\cdot), u^*(\cdot))\) \(~-\) оптимальная пара, \(\mathcal{H}\) \(~-\) функция Гамильтона–Понтрягина. Тогда существует \(\psi^*:[t_0, t_1] \rightarrow \mathbb{R}^n \), \(\psi^* \neq 0 \) такое, что:
1) Сопряженная система (СС): \[\dot{\psi} = -\frac{\partial H(\psi(t), x(t), u(t))}{\partial x(t)} \bigg|_{x=x^*(t) \\ u=u^*(t) \\ \psi = \psi^*(t)};\] 2) Условие максимума (УМ): \[u^*(t) \stackrel{\textrm{п.в.}}{\in} \underset{u \in \cal{P}}{\text{Argmax}} \, \mathcal{H}(\psi^*(t), x^*(t), u(t));\] 3) \[M(\psi^*(t), x^*(t)) \equiv \text{const} \geqslant 0.\]
Доказательство принципа максимума Понтрягина можно найти в книге: Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976 [1].
В общем случае еще учитывается условие трансверсальности на концах, однако поскольку рассматриваемая задача быстродействия является задачей "из точки в точку", их можно опустить. Уточним, что в задаче быстродействия нецелесообразно вводит дополнительную координату в вектор \(x\) и сопряженную переменную \(\psi\), поскольку все условия, связанные с этой дополнительной координатой, равны нулю или не имеют значения.
Важно отметить, что принцип максимума является необходимым, но не достаточным условием.
Примеры
Пример 1
Рассмотрим поезд, движущийся по железной дороге. Задача состоит в том, чтобы привести поезд на станцию и остановить его там за кратчайшее время. Положение поезда описывается действительной координатой \(x^1\); начало отсчета \(0\) соответствует станции. Будем считать, что поезд движется без трения, а мы управляем ускорением поезда, прикладывая ограниченную по модулю силу. Подберем единицы измерения так, чтобы максимальное по модулю ускорение было единичным. Тогда система описывается уравнениями: \[ \begin{cases} \ddot{x} = u, \\ x(0) = x^0, \\ x(t_1) = 0; \\ u \in [-1, 1]. \end{cases} \]
Или, в стандартном виде: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = u, \\ x_1(0) = x_1^0, \\ x_2(0) = x_2^0, \\ x_1(t_1) = 0, \\ x_2(t_1) = 0, \\ u \in [-1, 1]. \end{cases} \]
Решение: Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H} = \psi_1x_2 + \psi_2u. \]
Тогда сопряженная система имеет вид: \[ \begin{cases} \dot{\psi}_1 = 0, \\ \dot{\psi}_2 = -\psi_1. \end{cases} \]
Из условия максимума имеем, что: \[ u^*(t) = \text{sgn}\, (\psi_2(t)). \] Поскольку \(\ddot{\psi}_2 = 0\), то \(\psi_2 = \alpha +\beta t \), а значит \(u^*(t) = \text{sgn}\, (\alpha +\beta t)\). Следовательно, \(u(t)\) кусочно постоянно, принимает только экстремальные значения \(\pm 1\) и имеет не более одного переключения (точки разрыва).
Отыщем все траектории, соответствующие таким управлениям и приходящие в нуль. Найдем решения следующей системы: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = \pm1. \end{cases} \]
\[ x_1 = \pm\frac{x_2^2}{2}+C, C = const \]
Из семейства функций, являющихся решением, найдем те, которые не имеют переключений: \[ x_1 = \frac{x_2^2}{2}, x_2 < 0, \dot{x}_2 > 0; \\ x_1 = -\frac{x_2^2}{2}, x_2 > 0, \dot{x}_2 < 0. \]
Выпишем уравнения для траекторий, когда имеется одно переключение. Пусть \((p, q)\) \(~-\) точка переключения, тогда траектории можно записать как:
\[ x_1 = \begin{cases} -\frac{x_2^2}{2} + \frac{q^2}{2} + p, x_2 > q, \dot{x}_2 < 0, \\ \frac{x_2^2}{2}, 0 > x_2 > q, \dot{x}_2 > 0, \end{cases} \]
\[ x_1 = \begin{cases} \frac{x_2^2}{2} - \frac{q^2}{2} + p, x_2 < q, \dot{x}_2 > 0, \\ -\frac{x_2^2}{2}, 0 < x_2 < q, \dot{x}_2 < 0. \end{cases} \]
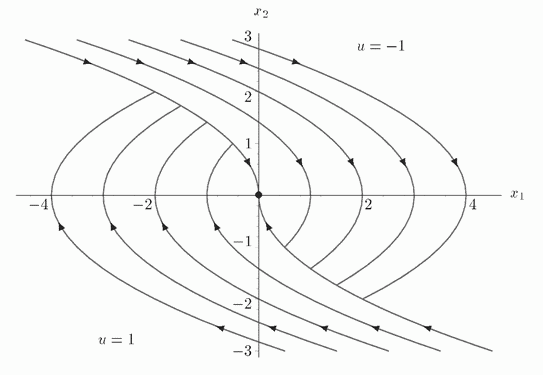
Все траектории можно изобразить на графике:
Поскольку через любую точку вида \((x_1, x_2)\) проходит единственная кривая из представленных, то для любой начальной точки существует единственная траектория, переводящая ей в конечную. Оптимальные траектории существуют, значит и решение оптимально.
Пример 2
Решим следующую задачу быстродействия: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = -x_1 + u, \\ x(0) = x^0, \\ x(t_1) = 0; \\ u \in [-1, 1]. \end{cases} \]
Решение: Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H} = \psi_1x_2 - \psi_2x_1 + \psi_2u. \]
Тогда сопряженная система имеет вид: \[ \begin{cases} \dot{\psi}_1 = \psi_2, \\ \dot{\psi}_2 = -\psi_1. \end{cases} \]
Из условия максимума имеем, что оптимальное управление: \[ u^*(t) = \text{sgn}(\psi_2(t)). \]
Так как \(\ddot{\psi}_2 = \psi_2\), то \(\psi_2 = \alpha\, \text{sin}(t+\beta), \alpha, \beta = const\). При этом \(\alpha \neq 0\), поскольку иначе \(\psi_2 = 0 \rightarrow \psi_1 = 0\) (из сопряженной системы) \(~-\) а это противоречит принципу максимума.
Поскольку \(u^*(t) = \text{sgn}(\alpha\, \text{sin}(t+\beta))\), то переключения зависят от первого момента переключения \(\tau \in [0, t]\) и изначального знака \(\text{sgn}\, (u^*(0)) \in \{\pm1\} \). Сами переключения будут происходить через каждое \(\pi\) от начального переключения \(\tau\). Оптимальное управление принимает только значение \(\pm 1\), тогда траектории \((x_1(t), x_2(t)\) состоят из кусков, удовлетворяющих системе: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = -x_1\pm1, \end{cases} \] т.е. из дуг окружностей \((x_1 \pm 1)^2 + x_2^2 = C, C = const\).
Заметим, что существует закономерность: переключения происходят на полуокружностях \[ (x_1 + 1)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ (x_1 - 3)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ (x_1 + 5)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ (x_1 - 7)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ \] и так далее. Таким образом, кривую переключений можно выразить как \[ (x_1 + (2k-1))^2 + x_2^2 = 1, x_2 \geqslant 0, k \in \mathbb{N}\\ (x_1 - (2k-1))^2 + x_2^2 = 1, x_2 \leqslant 0, k \in \mathbb{N} \\ \]
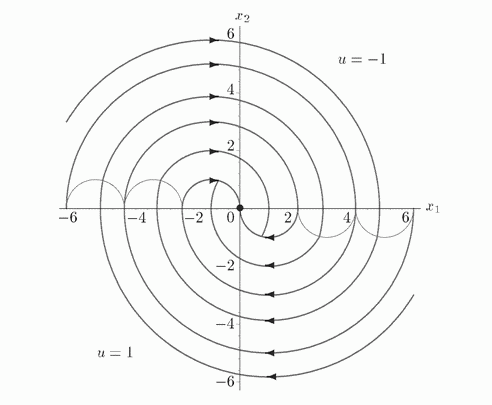
Все траектории можно изобразить на графике:
Поскольку для любой точки вида \((x_1, x_2)\) существует единственная кривая из семейства выше, то можно однозначно восстановить оптимальную траекторию.
Список литературы
- Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976,
- А.А. Аграчев, Ю.Л. Сачков. "Геометрическая теория управления". Москва, Физматлит, 2005