Гамильтоновы системы: различия между версиями
Timur23 (обсуждение | вклад) |
Timur23 (обсуждение | вклад) |
||
| (не показано 25 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | == | + | __TOC__ |
| − | Рассмотрим | + | == Первый интеграл системы == |
| + | === Определение === | ||
| + | Пусть $$x \in \mathbb{R}^n$$. Рассмотрим систему дифференциальных уравнений: | ||
| + | \begin{equation} | ||
| + | \label{s1} | ||
| + | \dot{x}_i = f_i(x_1, x_2, \dots, x_n), \quad | ||
| + | i = \overline{1, n}. | ||
| + | \end{equation} | ||
| + | '''Определение 1.''' | ||
| + | Пусть $$V(x_1, x_2,\dots, x_n)$$ — некоторая функция. Функция | ||
| + | \begin{gather*} | ||
| + | \dot{V}(x_1, x_2,\dots, x_n) = \sum_{i=1}^{n} \frac{\partial V}{\partial x_i} f_i(x) | ||
| + | \end{gather*} | ||
| + | называется '''производной функции $$V(x_1, x_2,\dots, x_n)$$ в силу системы (\ref{s1})'''. | ||
| + | |||
| + | '''Определение 2.''' | ||
| + | Функция $$V(x_1, x_2,\dots, x_n)$$ называется '''первым интегралом системы (\ref{s1})''', если $$V(x_1, x_2,\dots, x_n) = \mathrm{const}$$ или если её производная в силу системы равна нулю. | ||
| + | |||
| + | Первый интеграл системы (\ref{s1}) находится путем решения одного из следующих дифференциальных уравнений: | ||
| + | \begin{gather*} | ||
| + | \frac{dx_1}{f_1(x)} = \frac{dx_2}{f_2(x)} = \dots = \frac{dx_n}{f_n(x)}. | ||
| + | \end{gather*} | ||
| + | В качестве первого интеграла можно выбрать любую функцию из полученного семейства решений, но обычно выбирается функция с нулевой константой. | ||
| + | Всего таким способом можно получить $$(n-1)$$ функционально независимых первых интегралов. | ||
| + | |||
| + | С точки зрения физического смысла первый интеграл системы задает различные законы сохранения (энергии, импульса и т.п.). | ||
| + | |||
| + | [[Файл:Fp chistyakov.png|325px|мини|справа|Фазовый портрет системы]] | ||
| + | [[Файл:Lu chistyakov.png|325px|мини|справа|Линии уровня первого интеграла системы]] | ||
| + | |||
| + | ===Пример=== | ||
| + | |||
| + | Фазовые траектории системы обязаны лежать на линиях уровня первого интеграла. Убедимся в этом на примере. | ||
| + | |||
| + | Рассмотрим систему | ||
| + | \begin{equation} | ||
| + | \label{p1} | ||
| + | \begin{cases} | ||
| + | \dot{x}_1 = - x_2,\\ | ||
| + | \dot{x}_2 = x_1. | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | |||
| + | Найдем первый интеграл этой системы: | ||
| + | \begin{gather*} | ||
| + | - \frac{dx_1}{x_2} = \frac{dx_2}{x_1}, | ||
| + | \end{gather*} | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | V(x_1, x_2) = x_1^2 + x_2^2. | |
| + | \end{gather*} | ||
| + | Найдем производную в силу системы функции $$V(x_1, x_2)$$: | ||
| + | \begin{gather*} | ||
| + | \dot{V}(x_1, x_2) = - 2 x_1 x_2 + 2 x_2 x_1 \equiv 0. | ||
| + | \end{gather*} | ||
| + | Убедились в том, что найденная функция $$V(x_1, x_2)$$ является первым интегралом рассматриваемой системы. | ||
| + | |||
| + | Общее решение системы (\ref{p1}): | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | x_1(t) = C_1 \cos t + C_2 \sin t,\\ | ||
| + | x_2(t) = C_2 \cos t - C_1 \sin t. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | На графиках отчетливо видно, что фазовые траектории системы (\ref{p1}) лежат на линиях уровня найденного первого интеграла. | ||
| + | |||
| + | |||
| + | ==Гамильтоновы системы== | ||
| + | Рассмотрим уравнение Ньютона для материальной точки $$x \in \mathbb{R}^n$$, для простоты положим её массу равной 1: | ||
| + | \begin{gather*} | ||
| + | \ddot{x} = F(x),\quad x(0) = x_0,\quad \dot{x}(0) = p_0, \quad F(x) = \big(f_1(x), f_2(x), \dots, f_n(x)\big). | ||
\end{gather*} | \end{gather*} | ||
Это уравнение эквивалентно системе | Это уравнение эквивалентно системе | ||
| Строка 8: | Строка 75: | ||
\label{eq1} | \label{eq1} | ||
\begin{cases} | \begin{cases} | ||
| − | \dot{x} = | + | \dot{x}_i = p_i,\\ |
| − | \dot{p} = | + | \dot{p}_i = f_i(x). |
| − | + | \end{cases}, \quad | |
| + | i = \overline{1, n}. | ||
\end{equation} | \end{equation} | ||
| − | '''Определение | + | '''Определение 3.''' |
| − | + | Система '''потенциальна''', если существует функция $$U(x)$$, называемая '''потенциалом системы''' такая, что | |
| + | \begin{gather*} | ||
| + | \frac{dU(x)}{dx_i}=-f_i(x), \quad i = \overline{1, n}. | ||
| + | \end{gather*} | ||
| − | Далее | + | Потенциал определяется с точностью до произвольной постоянной. Далее будем предполагать, что $$f_i(x)$$ — [https://ru.wikipedia.org/wiki/%D0%9D%D0%B5%D0%BF%D1%80%D0%B5%D1%80%D1%8B%D0%B2%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F непрерывная функция], $$i = \overline{1, n}$$. |
| − | '''Определение | + | '''Определение 4.''' |
Первый интеграл системы (\ref{eq1}) называется '''гамильтонианом''' и определяется равенством | Первый интеграл системы (\ref{eq1}) называется '''гамильтонианом''' и определяется равенством | ||
\begin{equation} | \begin{equation} | ||
\label{eq2} | \label{eq2} | ||
| − | H(x, p) = \frac{ | + | H(x, p) = \sum_{i=1}^{n} \frac{p_i^2}{2} + U(x) = \mathrm{const} = C. |
\end{equation} | \end{equation} | ||
| − | + | Проверим, что это действительно первый интеграл системы (\ref{eq1}): | |
\begin{gather*} | \begin{gather*} | ||
| − | \frac{dH(x, p)}{dt} = \frac{\partial H}{\partial | + | \frac{dH(x, p)}{dt} = \sum_{i=1}^{n} \frac{\partial H}{\partial p_i}\dot{p}_i + \sum_{i=1}^{n} \frac{\partial H}{\partial x_i}\dot{x}_i = |
| + | \sum_{i=1}^{n} p_i f_i(x) + \sum_{i=1}^{n} -f_i(x) p_i \equiv 0. | ||
\end{gather*} | \end{gather*} | ||
| Строка 32: | Строка 104: | ||
Для того, чтобы отыскать значение постоянной $$C$$, которая отвечает движению с начальными данными $$x(0) = x_0, p(0) = p_0$$ достаточно вычислить | Для того, чтобы отыскать значение постоянной $$C$$, которая отвечает движению с начальными данными $$x(0) = x_0, p(0) = p_0$$ достаточно вычислить | ||
\begin{gather*} | \begin{gather*} | ||
| − | H(x_0, p_0) = \frac{ | + | H(x_0, p_0) = \sum_{i=1}^{n} \frac{p_{0, i}^2}{2} + U(x_0). |
\end{gather*} | \end{gather*} | ||
| − | + | '''Определение 5.''' | |
| − | |||
| − | '''Определение | ||
Пусть $$x, p \in \mathbb{R}^n$$. '''Гамильтоновой системой''' называется система вида | Пусть $$x, p \in \mathbb{R}^n$$. '''Гамильтоновой системой''' называется система вида | ||
\begin{equation} | \begin{equation} | ||
\label{eq3} | \label{eq3} | ||
\begin{cases} | \begin{cases} | ||
| − | \frac{dx_i}{dt} = \frac{\partial H}{\partial p_i}\\ | + | \displaystyle \frac{dx_i}{dt} = \frac{\partial H}{\partial p_i}, \\ |
| − | \frac{dp_i}{dt} = -\frac{\partial H}{\partial x_i} | + | \displaystyle \frac{dp_i}{dt} = -\frac{\partial H}{\partial x_i} |
\end{cases}, \quad | \end{cases}, \quad | ||
| − | i = \overline{1, n} | + | i = \overline{1, n}. |
| + | \end{equation} | ||
| + | |||
| + | == Примеры == | ||
| + | ===Пример 1=== | ||
| + | |||
| + | Рассмотрим уравнение одномерного движения частицы в потенциальном поле: | ||
| + | \begin{gather*} | ||
| + | \ddot{x} = f(x). | ||
| + | \end{gather*} | ||
| + | Перепишем это уравнение в виде системы дифференциальных уравнений: | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = p, \\ | ||
| + | \dot{p} = f(x). | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | Эта система потенциальна, и ее потенциал положим равным | ||
| + | \begin{gather*} | ||
| + | U(x) = - \int_{t_0}^x f(t) dt. | ||
| + | \end{gather*} | ||
| + | Тогда гамильтониан системы будет иметь вид: | ||
| + | \begin{gather*} | ||
| + | H(x, p) = U(x) + \frac{p^2}{2} = \int_{t_0}^x f(t) dt + \frac{p^2}{2}. | ||
| + | \end{gather*} | ||
| + | |||
| + | Выпишем уравнение для поиска траекторий системы. Пусть $$(x_0, p_0)$$ — начальные значения для переменных $$(x, p)$$. Так как $$H(x, p) = \mathrm{const}$$ вдоль траектории системы, то уравнение для поиска траектории системы имеет следующий вид: | ||
| + | \begin{gather*} | ||
| + | H(x, p) = H(x_0, p_0) = H_0. | ||
| + | \end{gather*} | ||
| + | |||
| + | Или более подробно: | ||
| + | \begin{gather*} | ||
| + | U(x) + \frac{p^2}{2} = U(x_0)+ \frac{p_0^2}{2}. | ||
| + | \end{gather*} | ||
| + | [[Файл:Primer1 chistyakov.png|391px|мини|вправо|Поведение гамильтоновой системы из примера 1]] | ||
| + | Заметим, что если $$(x, p)$$ является решением этого уравнения, то и $$(x, -p)$$ будет решением этого уравнения. | ||
| + | |||
| + | Построим фазовые траектории системы. Стационарные состояния системы задаются следующей системой уравнений: | ||
| + | \begin{equation} | ||
| + | \label{ss} | ||
| + | \begin{cases} | ||
| + | \displaystyle p = 0, \\ | ||
| + | \displaystyle f(x) = -\frac{dU(x)}{dx} = 0. | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | |||
| + | Начальный уровень энергии $$H_0$$ задает траекторию системы: | ||
| + | \begin{gather*} | ||
| + | U(x) + \frac{p^2}{2} = H_0, | ||
| + | \end{gather*} | ||
| + | \begin{equation} | ||
| + | \label{eq4} | ||
| + | p = \pm \sqrt{2\big(H_0 - U(x)\big)}. | ||
\end{equation} | \end{equation} | ||
| + | Уравнение (\ref{eq4}) задает траекторию движения в координатах $$(x, p)$$ для заданного начального значения энергии $$H_0$$. | ||
| + | |||
| + | Здесь и далее на верхнем графике показано поведение функции $$U(x)$$, а на нижнем — траектории движения в координатах $$(x, p)$$. Красными точками обозначены стационарные состояния системы, которые находятся из системы (\ref{ss}). Можно заметить, что в стационарных точках, соответствующих локальным максимумам функции $$U(x)$$, траектории ведут себя подобно седлу, а в точках, соответствующих локальным минимумам функции $$U(x)$$ — подобно центрам. Подробнее об этих видах стационарных точек можно прочитать в [https://sawiki.cs.msu.ru/index.php?title=Классификация_особых_точек_в_двумерном_пространстве этой статье]. | ||
| + | |||
| + | |||
| + | ===Пример 2=== | ||
| + | [[Файл:Primer2 chistyakov.png|391px|мини|вправо|Поведение гамильтоновой системы из примера 2]] | ||
| + | Рассмотрим колебания [https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D1%83%D0%B6%D0%B8%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA пружинного маятника], которые задаются следующим уравнением: | ||
| + | \begin{gather*} | ||
| + | \ddot{x} = -kx. | ||
| + | \end{gather*} | ||
| + | |||
| + | Перепишем это уравнение в виде системы дифференциальных уравнений: | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = p, \\ | ||
| + | \dot{p} = -kx. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | Аналогично Примеру 1 получаем: | ||
| + | \begin{gather*} | ||
| + | U(x) = \int_{t_0}^x kt dt = \frac{kx^2}{2}, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | H(x, p) = U(x) + \frac{p^2}{2} = \frac{kx^2}{2} + \frac{p^2}{2}, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | p = \pm \sqrt{2\big(H_0 - \frac{kx^2}{2}\big)}. | ||
| + | \end{gather*} | ||
| + | |||
| + | |||
| + | ===Пример 3=== | ||
| + | [[Файл:Primer3 chistyakov.png|391px|мини|вправо|Поведение гамильтоновой системы из примера 3]] | ||
| + | Рассмотрим уравнение [https://ru.wikipedia.org/wiki/%D0%9C%D0%B0%D1%82%D0%B5%D0%BC%D0%B0%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B9_%D0%BC%D0%B0%D1%8F%D1%82%D0%BD%D0%B8%D0%BA математического маятника]: | ||
| + | \begin{gather*} | ||
| + | \ddot{x} = -k \sin x. | ||
| + | \end{gather*} | ||
| + | Перепишем это уравнение в виде системы дифференциальных уравнений: | ||
| + | \begin{gather*} | ||
| + | \begin{cases} | ||
| + | \dot{x} = p, \\ | ||
| + | \dot{p} = -k \sin x. | ||
| + | \end{cases} | ||
| + | \end{gather*} | ||
| + | Аналогично Примеру 1 получаем: | ||
| + | \begin{gather*} | ||
| + | U(x) = \int_{t_0}^x k \sin t dt = - k \cos x, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | H(x, p) = U(x) + \frac{p^2}{2} = - k \cos x + \frac{p^2}{2}, | ||
| + | \end{gather*} | ||
| + | \begin{gather*} | ||
| + | p = \pm \sqrt{2\big(H_0 + k \cos x\big)}. | ||
| + | \end{gather*} | ||
== Список литературы == | == Список литературы == | ||
# Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | ||
# Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011. | # Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011. | ||
Текущая версия на 04:06, 3 декабря 2023
Содержание
Первый интеграл системы
Определение
Пусть $$x \in \mathbb{R}^n$$. Рассмотрим систему дифференциальных уравнений: \begin{equation} \label{s1} \dot{x}_i = f_i(x_1, x_2, \dots, x_n), \quad i = \overline{1, n}. \end{equation} Определение 1. Пусть $$V(x_1, x_2,\dots, x_n)$$ — некоторая функция. Функция \begin{gather*} \dot{V}(x_1, x_2,\dots, x_n) = \sum_{i=1}^{n} \frac{\partial V}{\partial x_i} f_i(x) \end{gather*} называется производной функции $$V(x_1, x_2,\dots, x_n)$$ в силу системы (\ref{s1}).
Определение 2. Функция $$V(x_1, x_2,\dots, x_n)$$ называется первым интегралом системы (\ref{s1}), если $$V(x_1, x_2,\dots, x_n) = \mathrm{const}$$ или если её производная в силу системы равна нулю.
Первый интеграл системы (\ref{s1}) находится путем решения одного из следующих дифференциальных уравнений: \begin{gather*} \frac{dx_1}{f_1(x)} = \frac{dx_2}{f_2(x)} = \dots = \frac{dx_n}{f_n(x)}. \end{gather*} В качестве первого интеграла можно выбрать любую функцию из полученного семейства решений, но обычно выбирается функция с нулевой константой. Всего таким способом можно получить $$(n-1)$$ функционально независимых первых интегралов.
С точки зрения физического смысла первый интеграл системы задает различные законы сохранения (энергии, импульса и т.п.).
Пример
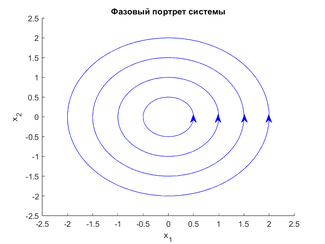
Фазовые траектории системы обязаны лежать на линиях уровня первого интеграла. Убедимся в этом на примере.
Рассмотрим систему \begin{equation} \label{p1} \begin{cases} \dot{x}_1 = - x_2,\\ \dot{x}_2 = x_1. \end{cases} \end{equation}
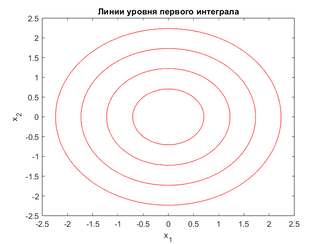
Найдем первый интеграл этой системы: \begin{gather*} - \frac{dx_1}{x_2} = \frac{dx_2}{x_1}, \end{gather*} \begin{gather*} V(x_1, x_2) = x_1^2 + x_2^2. \end{gather*} Найдем производную в силу системы функции $$V(x_1, x_2)$$: \begin{gather*} \dot{V}(x_1, x_2) = - 2 x_1 x_2 + 2 x_2 x_1 \equiv 0. \end{gather*} Убедились в том, что найденная функция $$V(x_1, x_2)$$ является первым интегралом рассматриваемой системы.
Общее решение системы (\ref{p1}): \begin{gather*} \begin{cases} x_1(t) = C_1 \cos t + C_2 \sin t,\\ x_2(t) = C_2 \cos t - C_1 \sin t. \end{cases} \end{gather*} На графиках отчетливо видно, что фазовые траектории системы (\ref{p1}) лежат на линиях уровня найденного первого интеграла.
Гамильтоновы системы
Рассмотрим уравнение Ньютона для материальной точки $$x \in \mathbb{R}^n$$, для простоты положим её массу равной 1: \begin{gather*} \ddot{x} = F(x),\quad x(0) = x_0,\quad \dot{x}(0) = p_0, \quad F(x) = \big(f_1(x), f_2(x), \dots, f_n(x)\big). \end{gather*} Это уравнение эквивалентно системе \begin{equation} \label{eq1} \begin{cases} \dot{x}_i = p_i,\\ \dot{p}_i = f_i(x). \end{cases}, \quad i = \overline{1, n}. \end{equation} Определение 3. Система потенциальна, если существует функция $$U(x)$$, называемая потенциалом системы такая, что \begin{gather*} \frac{dU(x)}{dx_i}=-f_i(x), \quad i = \overline{1, n}. \end{gather*}
Потенциал определяется с точностью до произвольной постоянной. Далее будем предполагать, что $$f_i(x)$$ — непрерывная функция, $$i = \overline{1, n}$$.
Определение 4. Первый интеграл системы (\ref{eq1}) называется гамильтонианом и определяется равенством \begin{equation} \label{eq2} H(x, p) = \sum_{i=1}^{n} \frac{p_i^2}{2} + U(x) = \mathrm{const} = C. \end{equation}
Проверим, что это действительно первый интеграл системы (\ref{eq1}): \begin{gather*} \frac{dH(x, p)}{dt} = \sum_{i=1}^{n} \frac{\partial H}{\partial p_i}\dot{p}_i + \sum_{i=1}^{n} \frac{\partial H}{\partial x_i}\dot{x}_i = \sum_{i=1}^{n} p_i f_i(x) + \sum_{i=1}^{n} -f_i(x) p_i \equiv 0. \end{gather*}
Гамильтониан задает полную энергию системы (\ref{eq1}), которая остается неизменной в течение всего времени эволюции системы. Для того, чтобы отыскать значение постоянной $$C$$, которая отвечает движению с начальными данными $$x(0) = x_0, p(0) = p_0$$ достаточно вычислить \begin{gather*} H(x_0, p_0) = \sum_{i=1}^{n} \frac{p_{0, i}^2}{2} + U(x_0). \end{gather*}
Определение 5. Пусть $$x, p \in \mathbb{R}^n$$. Гамильтоновой системой называется система вида \begin{equation} \label{eq3} \begin{cases} \displaystyle \frac{dx_i}{dt} = \frac{\partial H}{\partial p_i}, \\ \displaystyle \frac{dp_i}{dt} = -\frac{\partial H}{\partial x_i} \end{cases}, \quad i = \overline{1, n}. \end{equation}
Примеры
Пример 1
Рассмотрим уравнение одномерного движения частицы в потенциальном поле: \begin{gather*} \ddot{x} = f(x). \end{gather*} Перепишем это уравнение в виде системы дифференциальных уравнений: \begin{gather*} \begin{cases} \dot{x} = p, \\ \dot{p} = f(x). \end{cases} \end{gather*} Эта система потенциальна, и ее потенциал положим равным \begin{gather*} U(x) = - \int_{t_0}^x f(t) dt. \end{gather*} Тогда гамильтониан системы будет иметь вид: \begin{gather*} H(x, p) = U(x) + \frac{p^2}{2} = \int_{t_0}^x f(t) dt + \frac{p^2}{2}. \end{gather*}
Выпишем уравнение для поиска траекторий системы. Пусть $$(x_0, p_0)$$ — начальные значения для переменных $$(x, p)$$. Так как $$H(x, p) = \mathrm{const}$$ вдоль траектории системы, то уравнение для поиска траектории системы имеет следующий вид: \begin{gather*} H(x, p) = H(x_0, p_0) = H_0. \end{gather*}
Или более подробно: \begin{gather*} U(x) + \frac{p^2}{2} = U(x_0)+ \frac{p_0^2}{2}. \end{gather*}
Заметим, что если $$(x, p)$$ является решением этого уравнения, то и $$(x, -p)$$ будет решением этого уравнения.
Построим фазовые траектории системы. Стационарные состояния системы задаются следующей системой уравнений: \begin{equation} \label{ss} \begin{cases} \displaystyle p = 0, \\ \displaystyle f(x) = -\frac{dU(x)}{dx} = 0. \end{cases} \end{equation}
Начальный уровень энергии $$H_0$$ задает траекторию системы: \begin{gather*} U(x) + \frac{p^2}{2} = H_0, \end{gather*} \begin{equation} \label{eq4} p = \pm \sqrt{2\big(H_0 - U(x)\big)}. \end{equation} Уравнение (\ref{eq4}) задает траекторию движения в координатах $$(x, p)$$ для заданного начального значения энергии $$H_0$$.
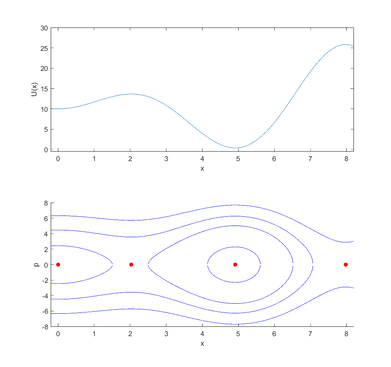
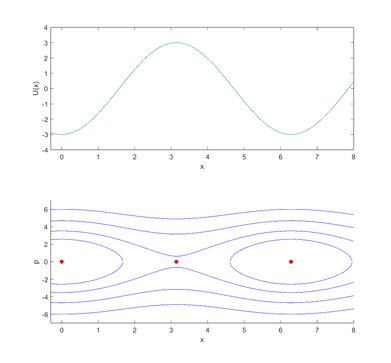
Здесь и далее на верхнем графике показано поведение функции $$U(x)$$, а на нижнем — траектории движения в координатах $$(x, p)$$. Красными точками обозначены стационарные состояния системы, которые находятся из системы (\ref{ss}). Можно заметить, что в стационарных точках, соответствующих локальным максимумам функции $$U(x)$$, траектории ведут себя подобно седлу, а в точках, соответствующих локальным минимумам функции $$U(x)$$ — подобно центрам. Подробнее об этих видах стационарных точек можно прочитать в этой статье.
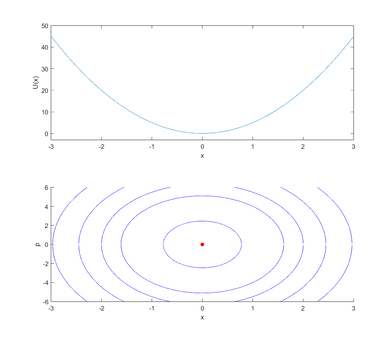
Пример 2
Рассмотрим колебания пружинного маятника, которые задаются следующим уравнением: \begin{gather*} \ddot{x} = -kx. \end{gather*}
Перепишем это уравнение в виде системы дифференциальных уравнений: \begin{gather*} \begin{cases} \dot{x} = p, \\ \dot{p} = -kx. \end{cases} \end{gather*} Аналогично Примеру 1 получаем: \begin{gather*} U(x) = \int_{t_0}^x kt dt = \frac{kx^2}{2}, \end{gather*} \begin{gather*} H(x, p) = U(x) + \frac{p^2}{2} = \frac{kx^2}{2} + \frac{p^2}{2}, \end{gather*} \begin{gather*} p = \pm \sqrt{2\big(H_0 - \frac{kx^2}{2}\big)}. \end{gather*}
Пример 3
Рассмотрим уравнение математического маятника: \begin{gather*} \ddot{x} = -k \sin x. \end{gather*} Перепишем это уравнение в виде системы дифференциальных уравнений: \begin{gather*} \begin{cases} \dot{x} = p, \\ \dot{p} = -k \sin x. \end{cases} \end{gather*} Аналогично Примеру 1 получаем: \begin{gather*} U(x) = \int_{t_0}^x k \sin t dt = - k \cos x, \end{gather*} \begin{gather*} H(x, p) = U(x) + \frac{p^2}{2} = - k \cos x + \frac{p^2}{2}, \end{gather*} \begin{gather*} p = \pm \sqrt{2\big(H_0 + k \cos x\big)}. \end{gather*}
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.