Классификация особых точек в двумерном пространстве: различия между версиями
Valeria23 (обсуждение | вклад) |
Valeria23 (обсуждение | вклад) |
||
| (не показаны 62 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | ==Постановка задачи== | ||
| + | Рассмотрим автономную систему | ||
| + | \begin{equation} \label{sist5} | ||
| + | \dfrac{d\overline{y}(t)}{dt} = \overline{f}(\overline{y}(t)). | ||
| + | \end{equation} | ||
| + | Введем матрицу производных | ||
| + | \begin{equation} \label{sist6} | ||
| + | A = (a_{ij}), \ \ a_{ij} = \dfrac{\partial f_i}{\partial y_j}(\overline{y_0}), \ \ i,j = 1, ..., n. | ||
| + | \end{equation} | ||
| + | Пусть матрица (\ref{sist6}) имеет ровно $$n$$ попарно различных собственных значений с ненулевой вещественной частью. Оказывается, что качественное поведение траекторий системы (\ref{sist5}) достаточно полно описывается с помощью линейной системы | ||
| + | \begin{equation} \label{sist7} | ||
| + | \dfrac{d\hat{y}(t)}{dt} = A\hat{y}(t) | ||
| + | \end{equation} | ||
| + | в малой окрестности каждой точки покоя $$\overline{y_0} \in \mathbb{R}^n$$ автономной системы. | ||
| − | == | + | ==Классификация точек покоя линейных систем== |
| − | Рассмотрим линейную систему с | + | Рассмотрим линейную систему с $$a_{ij} \in \mathbb{R}$$ относительно вектор-функции $$\overline{y}(t) = (y_1(t), y_2(t))^T$$ |
\begin{equation} \label{sist1} | \begin{equation} \label{sist1} | ||
\dfrac{d\overline{y}}{dt} = A\overline{y}, \ \ A = \left(\ | \dfrac{d\overline{y}}{dt} = A\overline{y}, \ \ A = \left(\ | ||
| Строка 9: | Строка 23: | ||
\end{array}\right) . | \end{array}\right) . | ||
\end{equation} | \end{equation} | ||
| − | + | Заметим, что [https://sawiki.cs.msu.ru/index.php/%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D1%8B%D0%B5_%D0%B8_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BA%D1%80%D0%B8%D0%B2%D1%8B%D0%B5._%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE фазовые траектории] этой системы являются [https://sawiki.cs.msu.ru/index.php/%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D1%8B%D0%B5_%D0%B8_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BA%D1%80%D0%B8%D0%B2%D1%8B%D0%B5._%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE интегральными кривыми] обыкновенного дифференциального уравнения, полученного после исключения переменной $$t$$ из (\ref{sist1}) | |
\begin{equation} \label{sist2} | \begin{equation} \label{sist2} | ||
\dfrac{dy_1}{dy_2} = \dfrac{a_{11}y_1+a_{12}y_2}{a_{21}y_1+a_{22}y_2} . | \dfrac{dy_1}{dy_2} = \dfrac{a_{11}y_1+a_{12}y_2}{a_{21}y_1+a_{22}y_2} . | ||
| Строка 15: | Строка 29: | ||
Точка покоя $$(0,0)$$ является '''''особой''''' для для уравнения (\ref{sist2}), поскольку в ней нарушены условия [https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%9A%D0%BE%D1%88%D0%B8#%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D1%8B_%D0%BE_%D1%80%D0%B0%D0%B7%D1%80%D0%B5%D1%88%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B8_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%9A%D0%BE%D1%88%D0%B8_%D0%B4%D0%BB%D1%8F_%D0%9E%D0%94%D0%A3 теоремы существования и единственности решения задачи Коши]. Поэтому через точку $$(0,0)$$ может проходить как несколько фазовых кривых, так и ни одной. Таким образом, точка покоя $$(0,0)$$ исходной системы (\ref{sist1}) является особой точкой уравнения (\ref{sist2}) в фазовых переменных. | Точка покоя $$(0,0)$$ является '''''особой''''' для для уравнения (\ref{sist2}), поскольку в ней нарушены условия [https://ru.wikipedia.org/wiki/%D0%97%D0%B0%D0%B4%D0%B0%D1%87%D0%B0_%D0%9A%D0%BE%D1%88%D0%B8#%D0%A2%D0%B5%D0%BE%D1%80%D0%B5%D0%BC%D1%8B_%D0%BE_%D1%80%D0%B0%D0%B7%D1%80%D0%B5%D1%88%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D0%B8_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%9A%D0%BE%D1%88%D0%B8_%D0%B4%D0%BB%D1%8F_%D0%9E%D0%94%D0%A3 теоремы существования и единственности решения задачи Коши]. Поэтому через точку $$(0,0)$$ может проходить как несколько фазовых кривых, так и ни одной. Таким образом, точка покоя $$(0,0)$$ исходной системы (\ref{sist1}) является особой точкой уравнения (\ref{sist2}) в фазовых переменных. | ||
| − | Классификацию точек покоя будем проводить в зависимости от собственных значений и собственных векторов матрицы $$A$$. В рассматриваемом случае $$n=2$$ имеется два собственных значения $$\lambda_1, \lambda_2$$. Если $$\lambda_1 \neq \lambda_2,$$ то соответствующие собственные векторы | + | Классификацию точек покоя будем проводить в зависимости от [https://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D0%B1%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80 собственных значений] и [https://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D0%B1%D1%81%D1%82%D0%B2%D0%B5%D0%BD%D0%BD%D1%8B%D0%B9_%D0%B2%D0%B5%D0%BA%D1%82%D0%BE%D1%80 собственных векторов] матрицы $$A$$. В рассматриваемом случае $$n=2$$ имеется два собственных значения $$\lambda_1, \lambda_2$$. Если $$\lambda_1 \neq \lambda_2,$$ то соответствующие собственные векторы |
\[ | \[ | ||
\overline{h_1} = \left(\ | \overline{h_1} = \left(\ | ||
| Строка 30: | Строка 44: | ||
\end{array}\right). | \end{array}\right). | ||
\] | \] | ||
| − | линейно независимы и составляют базис в $$\mathbb{C}^{2}$$. Если $$\lambda_1 = \lambda_2,$$ то возможно существование как двух, так и одного линейно независимого собственного вектора. В последнем случае существует один присоединенный вектор, линейно независимый с собственным. Рассмотрим типы точек покоя в случае невырожденной матрицы $$A$$ $$(det A \neq 0)$$. | + | линейно независимы и составляют базис в $$\mathbb{C}^{2}$$. Если $$\lambda_1 = \lambda_2,$$ то возможно существование как двух, так и одного [https://ru.wikipedia.org/wiki/%D0%9B%D0%B8%D0%BD%D0%B5%D0%B9%D0%BD%D0%B0%D1%8F_%D0%BD%D0%B5%D0%B7%D0%B0%D0%B2%D0%B8%D1%81%D0%B8%D0%BC%D0%BE%D1%81%D1%82%D1%8C линейно независимого] собственного вектора. В последнем случае существует один присоединенный вектор, линейно независимый с собственным. Рассмотрим типы точек покоя в случае невырожденной матрицы $$A$$ $$(\mathrm{det} A \neq 0)$$. |
| − | ==Узел $$(\lambda_1, \lambda_2 \in \mathbb{R}, \lambda_1 \neq \lambda_2, \lambda_1 \cdot \lambda_2 > 0)$$== | + | |
| + | ===Узел $$(\lambda_1, \lambda_2 \in \mathbb{R}, \ \ \lambda_1 \neq \lambda_2, \ \ \lambda_1 \cdot \lambda_2 > 0)$$=== | ||
Общее решение системы (\ref{sist1}) имеет вид | Общее решение системы (\ref{sist1}) имеет вид | ||
\begin{equation} \label{sist3} | \begin{equation} \label{sist3} | ||
| Строка 41: | Строка 56: | ||
\dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{\lambda_1t} + C_2h_{12}\lambda_2e^{\lambda_2t}}{C_1h_{21}\lambda_1e^{\lambda_1t} + C_2h_{22}\lambda_2e^{\lambda_2t}} = \dfrac{C_1h_{11}\lambda_1 + C_2h_{12}\lambda_2e^{(\lambda_2 - \lambda_1)t}}{C_1h_{21}\lambda_1 + C_2h_{22}\lambda_2e^{(\lambda_2 - \lambda_1)t}}. | \dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{\lambda_1t} + C_2h_{12}\lambda_2e^{\lambda_2t}}{C_1h_{21}\lambda_1e^{\lambda_1t} + C_2h_{22}\lambda_2e^{\lambda_2t}} = \dfrac{C_1h_{11}\lambda_1 + C_2h_{12}\lambda_2e^{(\lambda_2 - \lambda_1)t}}{C_1h_{21}\lambda_1 + C_2h_{22}\lambda_2e^{(\lambda_2 - \lambda_1)t}}. | ||
\end{equation} | \end{equation} | ||
| − | Так как $$\lambda_2 - \lambda_1 < 0,$$ то при $$C_1 \neq 0$$ имеем $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac{h_{11}}{h_{21}}$$ при $$t \rightarrow +\infty$$, то есть касательный вектор фазовой траектории в пределе коллинеарен собственному вектору $$\overline{h_1}$$. Если же $$C_1 = 0$$, то | + | Так как $$\lambda_2 - \lambda_1 < 0,$$ то при $$C_1 \neq 0$$ имеем $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac{h_{11}}{h_{21}}$$ при $$t \rightarrow +\infty$$, то есть касательный вектор фазовой траектории в пределе [https://ru.wikipedia.org/wiki/%D0%9A%D0%BE%D0%BB%D0%BB%D0%B8%D0%BD%D0%B5%D0%B0%D1%80%D0%BD%D0%BE%D1%81%D1%82%D1%8C коллинеарен] собственному вектору $$\overline{h_1}$$. Если же $$C_1 = 0$$, то |
\[ | \[ | ||
\overline{y}(t) = C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}. | \overline{y}(t) = C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}. | ||
\] | \] | ||
Значит, фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h}_2$$, и приближается к точке покоя при $$t \rightarrow +\infty$$. | Значит, фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h}_2$$, и приближается к точке покоя при $$t \rightarrow +\infty$$. | ||
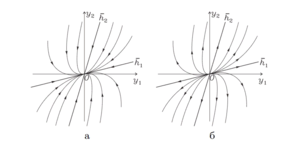
| − | [[Файл:Фазовые траектории узла- а - устойчивый, б - неустойчивый.png| | + | [[Файл:Фазовые траектории узла- а - устойчивый, б - неустойчивый.png|300px|мини|справа| Фазовые траектории узла: а — устойчивый, б — неустойчивый]] |
Выясним направление фазовых траекторий при $$t \rightarrow -\infty$$. В этом случае фазовые траектории, отличные от точки покоя, стремятся к бесконечно удаленной точке. В силу (\ref{sist3}) при $$C_2 \neq 0$$ имеем | Выясним направление фазовых траекторий при $$t \rightarrow -\infty$$. В этом случае фазовые траектории, отличные от точки покоя, стремятся к бесконечно удаленной точке. В силу (\ref{sist3}) при $$C_2 \neq 0$$ имеем | ||
\[ | \[ | ||
| Строка 55: | Строка 70: | ||
\overline{y}(t) = C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t}, | \overline{y}(t) = C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t}, | ||
\] | \] | ||
| − | и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1} | + | и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$. |
Для положительных собственных значений $$0 < \lambda_1 < \lambda_2$$ точка покоя называется '''''неустойчивым узлом''''', расположение и вид траекторий остаются теми же, что и для отрицательных собственных значений, но направление движения по траекториям меняется на противоположное. | Для положительных собственных значений $$0 < \lambda_1 < \lambda_2$$ точка покоя называется '''''неустойчивым узлом''''', расположение и вид траекторий остаются теми же, что и для отрицательных собственных значений, но направление движения по траекториям меняется на противоположное. | ||
Полезно помнить '''''правило узла''''': фазовые траектории входят в узел, касаясь собственного вектора с наименьшим по модулю собственным значением. | Полезно помнить '''''правило узла''''': фазовые траектории входят в узел, касаясь собственного вектора с наименьшим по модулю собственным значением. | ||
| − | ==Дикритический узел $$(\lambda_1 = \lambda_2 \neq 0, dim ker(A - \lambda_1E) = 2)$$== | + | |
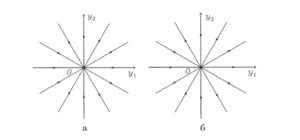
| − | [[Файл:Фазовые траектории дикритического узла- a - устойчивый, б - неустойчивый.png| | + | ====Дикритический узел $$(\lambda_1 = \lambda_2 \neq 0, \ \ \mathrm{dim \, ker}(A - \lambda_1E) = 2)$$==== |
| + | [[Файл:Фазовые траектории дикритического узла- a - устойчивый, б - неустойчивый.png|300px|мини|справа| Фазовые траектории дикритического узла: a — устойчивый, б — неустойчивый]] | ||
В случае дикритического узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечают два линейно независимых собственных вектора $$\overline{h_1}$$ и $$\overline{h_2}$$ матрицы $$A$$. Тогда выражение $$(\ref{sist3})$$ для общего решения принимает вид | В случае дикритического узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечают два линейно независимых собственных вектора $$\overline{h_1}$$ и $$\overline{h_2}$$ матрицы $$A$$. Тогда выражение $$(\ref{sist3})$$ для общего решения принимает вид | ||
\[ | \[ | ||
\overline{y}(t) = (C_1\overline{h_1} + C_2\overline{h_2})e^{\lambda t} | \overline{y}(t) = (C_1\overline{h_1} + C_2\overline{h_2})e^{\lambda t} | ||
\] | \] | ||
| − | и определяет на плоскости $$(y_1, y_2)$$ совокупность всевозможных лучей, | + | и определяет на плоскости $$(y_1, y_2)$$ совокупность всевозможных лучей. Выделяют два типа дикритических узла: '''''устойчивый дикритический узел''''', если лучи входят в точку покоя для $$\lambda < 0$$, при $$t \rightarrow +\infty$$, и '''''неустойчивый дикритический узел''''', если лучи выходят из точки покоя для $$\lambda > 0$$ , при $$t \rightarrow +\infty$$. |
| − | ==Вырожденный узел $$(\lambda_1 = \lambda_2 \neq 0, dim ker(A-\lambda_1E) = 1)$$== | + | |
| − | Вырожденный узел '''''устойчив''''', если $$\lambda_1 = \lambda_2 < 0$$, и '''''неустойчив''''', если $$\lambda_1 = \lambda_2 > 0$$. В случае вырожденного узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечает один собственный вектор $$\overline{h_1}$$ | + | ====Вырожденный узел $$(\lambda_1 = \lambda_2 \neq 0,\ \ \mathrm{dim \, ker}(A-\lambda_1E) = 1)$$==== |
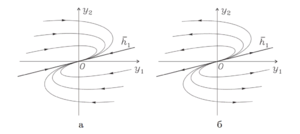
| + | [[Файл:Фазовые траектории вырожденного узла.png|300px|мини|справа| Фазовые траектории вырожденного узла: а — устойчивый, б — неустойчивый]] | ||
| + | Вырожденный узел '''''устойчив''''', если $$\lambda_1 = \lambda_2 < 0$$, и '''''неустойчив''''', если $$\lambda_1 = \lambda_2 > 0$$. В случае вырожденного узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечает один собственный вектор $$\overline{h_1}$$ матрицы $$A$$ и один присоединенный вектор $$\overline{p_1}$$. Общее решение системы (\ref{sist1}) записывается в виде | ||
\[ | \[ | ||
\overline{y}(t) = C_1\overline{h_1}e^{\lambda t} + C_2(\overline{p_1} + t\overline{h_1})e^{\lambda t}. | \overline{y}(t) = C_1\overline{h_1}e^{\lambda t} + C_2(\overline{p_1} + t\overline{h_1})e^{\lambda t}. | ||
\] | \] | ||
| − | |||
Если $$C_2 = 0$$, то фазовые траектории решения $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda t}$$ состоят из двух лучей, входящих в точку покоя для $$\lambda < 0$$ (выходящих из точки покоя для $$\lambda > 0$$) при $$t \rightarrow +\infty$$ по направлению собственного вектора. | Если $$C_2 = 0$$, то фазовые траектории решения $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda t}$$ состоят из двух лучей, входящих в точку покоя для $$\lambda < 0$$ (выходящих из точки покоя для $$\lambda > 0$$) при $$t \rightarrow +\infty$$ по направлению собственного вектора. | ||
| Строка 79: | Строка 96: | ||
\overline{y}(t) = te^{\lambda t}(C_2\overline{h_1} + \overline{o}(1)), \ \ t \rightarrow +\infty. | \overline{y}(t) = te^{\lambda t}(C_2\overline{h_1} + \overline{o}(1)), \ \ t \rightarrow +\infty. | ||
\] | \] | ||
| − | Видно, что решение касается собственного вектора в точке покоя при $$t \rightarrow +\infty$$ для $$\lambda < 0$$, либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$. На бесконечности при $$t \rightarrow +\infty$$ для $$\lambda < 0$$ либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$ фазовая траектория опять выстраивается по направлению собственного вектора, но в противоположном направлении благодаря смене знака множителя $$t$$. | + | Видно, что решение касается собственного вектора в точке покоя при $$t \rightarrow +\infty$$ для $$\lambda < 0$$, либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$. На бесконечности при $$t \rightarrow +\infty$$ для $$\lambda < 0$$ либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$ фазовая траектория опять выстраивается по направлению собственного вектора, но в противоположном направлении благодаря смене знака множителя $$t$$. |
| − | ==Седло $$(\lambda_1,\lambda_2 \in \mathbb{R}, \lambda_2 < 0 < \lambda_1)$$== | + | |
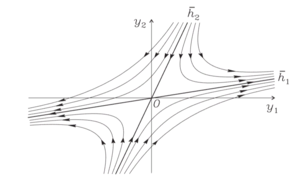
| − | [[Файл:2023-12-28 15-50-49.png|300px|мини|справа| | + | ===Седло $$(\lambda_1,\lambda_2 \in \mathbb{R},\ \ \lambda_2 < 0 < \lambda_1)$$=== |
| − | Ясно, что седло является [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B неустойчивой точкой покоя | + | [[Файл:2023-12-28 15-50-49.png|300px|мини|справа|Фазовые траектории седла.]] |
| + | Ясно, что седло является [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B неустойчивой] точкой покоя. Воспользуемся для анализа поведения траекторий формулой (\ref{sist3}). Для $$C_1 \neq 0 $$ при $$t \rightarrow +\infty$$ получаем представление | ||
\[ | \[ | ||
\overline{y}(t) = e^{\lambda_1 t}\left(C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix}e^{(\lambda_2-\lambda_1)t}\right) = e^{\lambda_1t}\left(C_1\begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + \overline{o}(1)\right). | \overline{y}(t) = e^{\lambda_1 t}\left(C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix}e^{(\lambda_2-\lambda_1)t}\right) = e^{\lambda_1t}\left(C_1\begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + \overline{o}(1)\right). | ||
| Строка 88: | Строка 106: | ||
Кроме того, из (\ref{sist4}) нетрудно видеть, что $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac {h_{11}}{h_{21}}$$, то есть фазовые траектории при $$t \rightarrow +\infty$$ стремятся к бесконечно удаленной точке и имеют асимптоту, задаваемую собственным вектором $$\overline{h_1}$$. Если же $$C_1 = 0$$, то $$\overline{y}(t) = C_2\overline{h_2}e^{\lambda_2t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_2}$$, приближаясь к точке покоя при $$t \rightarrow +\infty$$. | Кроме того, из (\ref{sist4}) нетрудно видеть, что $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac {h_{11}}{h_{21}}$$, то есть фазовые траектории при $$t \rightarrow +\infty$$ стремятся к бесконечно удаленной точке и имеют асимптоту, задаваемую собственным вектором $$\overline{h_1}$$. Если же $$C_1 = 0$$, то $$\overline{y}(t) = C_2\overline{h_2}e^{\lambda_2t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_2}$$, приближаясь к точке покоя при $$t \rightarrow +\infty$$. | ||
| − | Для $$t \rightarrow -\infty$$ картина противоположная: фазовые траектории стремятся к бесконечно удаленной точке при $$C_2 \neq 0$$ и имеют | + | Для $$t \rightarrow -\infty$$ картина противоположная: фазовые траектории стремятся к бесконечно удаленной точке при $$C_2 \neq 0$$ и имеют асимптоту, задаваемую вектором $$\overline{h_2}$$. Если $$C_2 = 0$$, то $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda_1t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$, приближаясь к точке покоя при $$t \rightarrow -\infty$$. |
| − | ==Фокус $$(\lambda_{1,2} = \delta \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0, \ \ \delta \neq 0)$$== | + | |
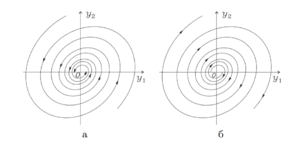
| − | [[Файл:2023-12-28 16-23-49.png| | + | ===Фокус $$(\lambda_{1,2} = \delta \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0, \ \ \delta \neq 0)$$=== |
| − | Точка покоя называется '''''фокусом''''', если матрица $$A$$ имеет комплексно сопряженные собственные значения с ненулевыми действительной и мнимой частями. Пусть $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ | + | [[Файл:2023-12-28 16-23-49.png|300px|мини|справа| Фазовые траектории фокуса: а — устойчивый, б — неусточивый]] |
| + | Точка покоя называется '''''фокусом''''', если матрица $$A$$ имеет комплексно сопряженные собственные значения с ненулевыми действительной и мнимой частями. Пусть $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ $$—$$ собственный вектор с линейно независимыми $$\overline{h_{1,2}}$$, отвечающие собственному значению $$\lambda_1 = \delta + i\omega$$. Тогда действительная и мнимая части комплекснозначной вектор-функции $$\overline{z} = \overline{h}e^{\lambda_1t}$$ составляют вещественную [https://ru.wikipedia.org/wiki/%D0%A4%D1%83%D0%BD%D0%B4%D0%B0%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D1%80%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B9 фундаментальную систему решений] системы | ||
\[ | \[ | ||
\left\{ \begin{array}{ccc} | \left\{ \begin{array}{ccc} | ||
| − | \overline{y_1}(t) = Re(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\cos{\omega t} - \overline{h_2}\sin{\omega t}), \\ | + | \overline{y_1}(t) = \mathrm{Re}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\cos{\omega t} - \overline{h_2}\sin{\omega t}), \\ |
| − | \overline{y_2}(t) = Im(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\sin{\omega t} + \overline{h_2}\cos{\omega t}).\\ | + | \overline{y_2}(t) = \mathrm{Im}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\sin{\omega t} + \overline{h_2}\cos{\omega t}).\\ |
\end{array} | \end{array} | ||
\right. | \right. | ||
| Строка 115: | Строка 134: | ||
\xi_1(t) = Ce^{\delta t}\sin{(\omega t + \psi)},\ \ \xi_2(t) = Ce^{\delta t}\cos{(\omega t + \psi)}, | \xi_1(t) = Ce^{\delta t}\sin{(\omega t + \psi)},\ \ \xi_2(t) = Ce^{\delta t}\cos{(\omega t + \psi)}, | ||
\] | \] | ||
| − | задающих логарифмическую спираль, | + | задающих [https://ru.wikipedia.org/wiki/%D0%9B%D0%BE%D0%B3%D0%B0%D1%80%D0%B8%D1%84%D0%BC%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D1%81%D0%BF%D0%B8%D1%80%D0%B0%D0%BB%D1%8C логарифмическую спираль]. Выделяют два типа фокусов: '''''устойчивый фокус''''' $$—$$ фокус, при котором логарифмическая спираль при $$t \rightarrow +\infty$$ скручивается для $$\delta < 0$$, и '''''неустойчивый фокус''''' $$—$$ фокус, при котором логарифмическая спираль раскручивается для $$\delta > 0$$ . |
| − | + | ===Центр $$(\lambda_{1,2} = \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0)$$=== | |
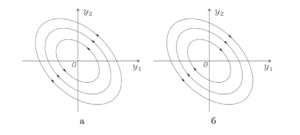
| − | ==Центр $$(\lambda_{1,2} = \pm i\omega \in \mathbb{C}, \omega \neq 0)$$== | + | [[Файл:2023-12-28 16-39-26.png|300px|мини|справа|Фазовые траектории центра.]] |
| − | Точка покоя называется '''''центром''''', если матрица $$A$$ имеет чисто мнимые комплексно сопряженные собственные значения. Таким образом, центр | + | Точка покоя называется '''''центром''''', если матрица $$A$$ имеет чисто мнимые комплексно сопряженные собственные значения. Таким образом, центр $$—$$ [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B устойчивая по Ляпунову] точка покоя, не являющаяся [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B асимптотически устойчивой]. С помощью комплекснозначного собственного вектора $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ с линейно независимыми вещественными составляющими $$\overline{h_1}$$ и $$\overline{h_2}$$ аналогично случаю фокуса запишем общее решение в виде разложения $$\overline{y}(t) = \xi_1(t)\overline{h_1} + \xi_2(t)\overline{h_2}$$ с коэффициентами |
\[ | \[ | ||
\xi_1(t) = C\sin{(\omega t + \psi)},\ \ \xi_2(t) = C\cos{(\omega t + \psi)}, | \xi_1(t) = C\sin{(\omega t + \psi)},\ \ \xi_2(t) = C\cos{(\omega t + \psi)}, | ||
\] | \] | ||
| − | удовлетворяющими равенству $$\xi_1^2(t) + \xi_2^2(t) = C^2$$. Тогда вектор | + | удовлетворяющими равенству $$\xi_1^2(t) + \xi_2^2(t) = C^2$$. Тогда вектор коэффициентов $$(\xi_1(t), \xi_2(t))$$ описывает периодическое движение по окружности. |
| + | ==Классификация точек покоя нелинейной системы== | ||
| + | Вернемся к нелинейной системе. Заметим, что на плоскости $$(n=2)$$ точке покоя соответствует линейная система вида (\ref{sist7}), имеющая нулевую точку покоя только для одного из следующих типов: узел, седло или фокус. Будем называть точку покоя '''''узлом''''', '''''седлом''''' или '''''фокусом''''', если этот тип имеет нулевая точка покоя соответствующей линейной системы (\ref{sist7}) с матрицей (\ref{sist6}). | ||
| + | |||
| + | ==Список литературы== | ||
| + | # Денисов А.М., Разгулин А.В. "Обыкновенные дифференциальные уравнения", 2009. | ||
| + | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | ||
Текущая версия на 11:59, 29 декабря 2023
Содержание
- 1 Постановка задачи
- 2 Классификация точек покоя линейных систем
- 2.1 Узел $$(\lambda_1, \lambda_2 \in \mathbb{R}, \ \ \lambda_1 \neq \lambda_2, \ \ \lambda_1 \cdot \lambda_2 > 0)$$
- 2.2 Седло $$(\lambda_1,\lambda_2 \in \mathbb{R},\ \ \lambda_2 < 0 < \lambda_1)$$
- 2.3 Фокус $$(\lambda_{1,2} = \delta \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0, \ \ \delta \neq 0)$$
- 2.4 Центр $$(\lambda_{1,2} = \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0)$$
- 3 Классификация точек покоя нелинейной системы
- 4 Список литературы
Постановка задачи
Рассмотрим автономную систему \begin{equation} \label{sist5} \dfrac{d\overline{y}(t)}{dt} = \overline{f}(\overline{y}(t)). \end{equation} Введем матрицу производных \begin{equation} \label{sist6} A = (a_{ij}), \ \ a_{ij} = \dfrac{\partial f_i}{\partial y_j}(\overline{y_0}), \ \ i,j = 1, ..., n. \end{equation} Пусть матрица (\ref{sist6}) имеет ровно $$n$$ попарно различных собственных значений с ненулевой вещественной частью. Оказывается, что качественное поведение траекторий системы (\ref{sist5}) достаточно полно описывается с помощью линейной системы \begin{equation} \label{sist7} \dfrac{d\hat{y}(t)}{dt} = A\hat{y}(t) \end{equation} в малой окрестности каждой точки покоя $$\overline{y_0} \in \mathbb{R}^n$$ автономной системы.
Классификация точек покоя линейных систем
Рассмотрим линейную систему с $$a_{ij} \in \mathbb{R}$$ относительно вектор-функции $$\overline{y}(t) = (y_1(t), y_2(t))^T$$ \begin{equation} \label{sist1} \dfrac{d\overline{y}}{dt} = A\overline{y}, \ \ A = \left(\ \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22}\\ \end{array}\right) . \end{equation} Заметим, что фазовые траектории этой системы являются интегральными кривыми обыкновенного дифференциального уравнения, полученного после исключения переменной $$t$$ из (\ref{sist1}) \begin{equation} \label{sist2} \dfrac{dy_1}{dy_2} = \dfrac{a_{11}y_1+a_{12}y_2}{a_{21}y_1+a_{22}y_2} . \end{equation} Точка покоя $$(0,0)$$ является особой для для уравнения (\ref{sist2}), поскольку в ней нарушены условия теоремы существования и единственности решения задачи Коши. Поэтому через точку $$(0,0)$$ может проходить как несколько фазовых кривых, так и ни одной. Таким образом, точка покоя $$(0,0)$$ исходной системы (\ref{sist1}) является особой точкой уравнения (\ref{sist2}) в фазовых переменных.
Классификацию точек покоя будем проводить в зависимости от собственных значений и собственных векторов матрицы $$A$$. В рассматриваемом случае $$n=2$$ имеется два собственных значения $$\lambda_1, \lambda_2$$. Если $$\lambda_1 \neq \lambda_2,$$ то соответствующие собственные векторы \[ \overline{h_1} = \left(\ \begin{array}{ccc} h_{11} \\ h_{21}\\ \end{array}\right), \] \[ \overline{h_2} = \left(\ \begin{array}{ccc} h_{12} \\ h_{22}\\ \end{array}\right). \] линейно независимы и составляют базис в $$\mathbb{C}^{2}$$. Если $$\lambda_1 = \lambda_2,$$ то возможно существование как двух, так и одного линейно независимого собственного вектора. В последнем случае существует один присоединенный вектор, линейно независимый с собственным. Рассмотрим типы точек покоя в случае невырожденной матрицы $$A$$ $$(\mathrm{det} A \neq 0)$$.
Узел $$(\lambda_1, \lambda_2 \in \mathbb{R}, \ \ \lambda_1 \neq \lambda_2, \ \ \lambda_1 \cdot \lambda_2 > 0)$$
Общее решение системы (\ref{sist1}) имеет вид \begin{equation} \label{sist3} y(t) = \begin{pmatrix} y_1(t) \\ y_2(t) \end{pmatrix} = С_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t} + С_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}, \ \ \forall C_1, C_2 \in \mathbb{R}. \end{equation}
Рассмотрим сначала случай, когда собственные значения отрицательны: $$\lambda_2 < \lambda_1 < 0.$$ Тогда нулевая точка покоя асимптотически устойчива по Ляпунову и называется устойчивым узлом. Фазовые кривые при $$t \rightarrow +\infty$$ стремятся к устойчивому узлу: $$\overline{y}(t) \rightarrow \overline{\Theta}$$. Выясним, по какому направлению фазовые траектории входят в узел. Для этого вычислим производную \begin{equation} \label{sist4} \dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{\lambda_1t} + C_2h_{12}\lambda_2e^{\lambda_2t}}{C_1h_{21}\lambda_1e^{\lambda_1t} + C_2h_{22}\lambda_2e^{\lambda_2t}} = \dfrac{C_1h_{11}\lambda_1 + C_2h_{12}\lambda_2e^{(\lambda_2 - \lambda_1)t}}{C_1h_{21}\lambda_1 + C_2h_{22}\lambda_2e^{(\lambda_2 - \lambda_1)t}}. \end{equation} Так как $$\lambda_2 - \lambda_1 < 0,$$ то при $$C_1 \neq 0$$ имеем $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac{h_{11}}{h_{21}}$$ при $$t \rightarrow +\infty$$, то есть касательный вектор фазовой траектории в пределе коллинеарен собственному вектору $$\overline{h_1}$$. Если же $$C_1 = 0$$, то \[ \overline{y}(t) = C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}. \] Значит, фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h}_2$$, и приближается к точке покоя при $$t \rightarrow +\infty$$.
Выясним направление фазовых траекторий при $$t \rightarrow -\infty$$. В этом случае фазовые траектории, отличные от точки покоя, стремятся к бесконечно удаленной точке. В силу (\ref{sist3}) при $$C_2 \neq 0$$ имеем \[ \dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{(\lambda_1-\lambda_2)t} + C_2h_{12}\lambda_2}{C_1h_{21}\lambda_1e^{(\lambda_1-\lambda_2)t} + C_2h_{22}\lambda_2} \rightarrow \dfrac{h_{12}}{h_{22}}, \ \ t \rightarrow -\infty, \ \ (\lambda_1 - \lambda_2 > 0), \] то есть траектории в окрестности бесконечно удаленной точки выстраиваются параллельно вектору $$\overline{h_2}$$. Если же $$C_2 = 0$$, то \[ \overline{y}(t) = C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t}, \] и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$.
Для положительных собственных значений $$0 < \lambda_1 < \lambda_2$$ точка покоя называется неустойчивым узлом, расположение и вид траекторий остаются теми же, что и для отрицательных собственных значений, но направление движения по траекториям меняется на противоположное.
Полезно помнить правило узла: фазовые траектории входят в узел, касаясь собственного вектора с наименьшим по модулю собственным значением.
Дикритический узел $$(\lambda_1 = \lambda_2 \neq 0, \ \ \mathrm{dim \, ker}(A - \lambda_1E) = 2)$$
В случае дикритического узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечают два линейно независимых собственных вектора $$\overline{h_1}$$ и $$\overline{h_2}$$ матрицы $$A$$. Тогда выражение $$(\ref{sist3})$$ для общего решения принимает вид \[ \overline{y}(t) = (C_1\overline{h_1} + C_2\overline{h_2})e^{\lambda t} \] и определяет на плоскости $$(y_1, y_2)$$ совокупность всевозможных лучей. Выделяют два типа дикритических узла: устойчивый дикритический узел, если лучи входят в точку покоя для $$\lambda < 0$$, при $$t \rightarrow +\infty$$, и неустойчивый дикритический узел, если лучи выходят из точки покоя для $$\lambda > 0$$ , при $$t \rightarrow +\infty$$.
Вырожденный узел $$(\lambda_1 = \lambda_2 \neq 0,\ \ \mathrm{dim \, ker}(A-\lambda_1E) = 1)$$
Вырожденный узел устойчив, если $$\lambda_1 = \lambda_2 < 0$$, и неустойчив, если $$\lambda_1 = \lambda_2 > 0$$. В случае вырожденного узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечает один собственный вектор $$\overline{h_1}$$ матрицы $$A$$ и один присоединенный вектор $$\overline{p_1}$$. Общее решение системы (\ref{sist1}) записывается в виде \[ \overline{y}(t) = C_1\overline{h_1}e^{\lambda t} + C_2(\overline{p_1} + t\overline{h_1})e^{\lambda t}. \] Если $$C_2 = 0$$, то фазовые траектории решения $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda t}$$ состоят из двух лучей, входящих в точку покоя для $$\lambda < 0$$ (выходящих из точки покоя для $$\lambda > 0$$) при $$t \rightarrow +\infty$$ по направлению собственного вектора.
Если $$C_2 \neq 0$$, то \[ \overline{y}(t) = te^{\lambda t}(C_2\overline{h_1} + \overline{o}(1)), \ \ t \rightarrow +\infty. \] Видно, что решение касается собственного вектора в точке покоя при $$t \rightarrow +\infty$$ для $$\lambda < 0$$, либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$. На бесконечности при $$t \rightarrow +\infty$$ для $$\lambda < 0$$ либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$ фазовая траектория опять выстраивается по направлению собственного вектора, но в противоположном направлении благодаря смене знака множителя $$t$$.
Седло $$(\lambda_1,\lambda_2 \in \mathbb{R},\ \ \lambda_2 < 0 < \lambda_1)$$
Ясно, что седло является неустойчивой точкой покоя. Воспользуемся для анализа поведения траекторий формулой (\ref{sist3}). Для $$C_1 \neq 0 $$ при $$t \rightarrow +\infty$$ получаем представление \[ \overline{y}(t) = e^{\lambda_1 t}\left(C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix}e^{(\lambda_2-\lambda_1)t}\right) = e^{\lambda_1t}\left(C_1\begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + \overline{o}(1)\right). \] Кроме того, из (\ref{sist4}) нетрудно видеть, что $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac {h_{11}}{h_{21}}$$, то есть фазовые траектории при $$t \rightarrow +\infty$$ стремятся к бесконечно удаленной точке и имеют асимптоту, задаваемую собственным вектором $$\overline{h_1}$$. Если же $$C_1 = 0$$, то $$\overline{y}(t) = C_2\overline{h_2}e^{\lambda_2t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_2}$$, приближаясь к точке покоя при $$t \rightarrow +\infty$$.
Для $$t \rightarrow -\infty$$ картина противоположная: фазовые траектории стремятся к бесконечно удаленной точке при $$C_2 \neq 0$$ и имеют асимптоту, задаваемую вектором $$\overline{h_2}$$. Если $$C_2 = 0$$, то $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda_1t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$, приближаясь к точке покоя при $$t \rightarrow -\infty$$.
Фокус $$(\lambda_{1,2} = \delta \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0, \ \ \delta \neq 0)$$
Точка покоя называется фокусом, если матрица $$A$$ имеет комплексно сопряженные собственные значения с ненулевыми действительной и мнимой частями. Пусть $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ $$—$$ собственный вектор с линейно независимыми $$\overline{h_{1,2}}$$, отвечающие собственному значению $$\lambda_1 = \delta + i\omega$$. Тогда действительная и мнимая части комплекснозначной вектор-функции $$\overline{z} = \overline{h}e^{\lambda_1t}$$ составляют вещественную фундаментальную систему решений системы \[ \left\{ \begin{array}{ccc} \overline{y_1}(t) = \mathrm{Re}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\cos{\omega t} - \overline{h_2}\sin{\omega t}), \\ \overline{y_2}(t) = \mathrm{Im}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\sin{\omega t} + \overline{h_2}\cos{\omega t}).\\ \end{array} \right. \] Поэтому общее вещественное решение имеет вид \[ \overline{y}(t) = C_1\overline{y_1}(t) + C_2\overline{y_2}(t) = e^{\delta t}(C_2\sin{\omega t} + C_1\cos{\omega t})\overline{h_1} + e^{\delta t}(C_2\cos{\omega t} - C_1\sin{\omega t})\overline{h_2}. \] Обозначая $$C = \sqrt{{C_1}^2 + {C_2}^2} \neq 0$$ и вводя вспомогательный угол $$\psi$$ из условий \[ \sin{\psi} = \dfrac{C_1}{C}, \ \ \cos{\psi} = \dfrac{C_2}{C}, \] приходим к разложению решения по базису, составленному из векторов $$\overline{h_1}$$ и $$\overline{h_2}$$ \[ \overline{y}(t) = \xi_1(t)\overline{h_1} + \xi_2(t)\overline{h_2}. \] Коэффициенты разложения определяются из соотношений \[ \xi_1(t) = Ce^{\delta t}\sin{(\omega t + \psi)},\ \ \xi_2(t) = Ce^{\delta t}\cos{(\omega t + \psi)}, \] задающих логарифмическую спираль. Выделяют два типа фокусов: устойчивый фокус $$—$$ фокус, при котором логарифмическая спираль при $$t \rightarrow +\infty$$ скручивается для $$\delta < 0$$, и неустойчивый фокус $$—$$ фокус, при котором логарифмическая спираль раскручивается для $$\delta > 0$$ .
Центр $$(\lambda_{1,2} = \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0)$$
Точка покоя называется центром, если матрица $$A$$ имеет чисто мнимые комплексно сопряженные собственные значения. Таким образом, центр $$—$$ устойчивая по Ляпунову точка покоя, не являющаяся асимптотически устойчивой. С помощью комплекснозначного собственного вектора $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ с линейно независимыми вещественными составляющими $$\overline{h_1}$$ и $$\overline{h_2}$$ аналогично случаю фокуса запишем общее решение в виде разложения $$\overline{y}(t) = \xi_1(t)\overline{h_1} + \xi_2(t)\overline{h_2}$$ с коэффициентами \[ \xi_1(t) = C\sin{(\omega t + \psi)},\ \ \xi_2(t) = C\cos{(\omega t + \psi)}, \] удовлетворяющими равенству $$\xi_1^2(t) + \xi_2^2(t) = C^2$$. Тогда вектор коэффициентов $$(\xi_1(t), \xi_2(t))$$ описывает периодическое движение по окружности.
Классификация точек покоя нелинейной системы
Вернемся к нелинейной системе. Заметим, что на плоскости $$(n=2)$$ точке покоя соответствует линейная система вида (\ref{sist7}), имеющая нулевую точку покоя только для одного из следующих типов: узел, седло или фокус. Будем называть точку покоя узлом, седлом или фокусом, если этот тип имеет нулевая точка покоя соответствующей линейной системы (\ref{sist7}) с матрицей (\ref{sist6}).
Список литературы
- Денисов А.М., Разгулин А.В. "Обыкновенные дифференциальные уравнения", 2009.
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.