Неограниченная продолжаемость решений ОДУ: различия между версиями
Anton (обсуждение | вклад) |
Anton (обсуждение | вклад) (→Пример) |
||
| (не показано 50 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | Будем рассматривать | + | Будем рассматривать систему обыкновенных дифференциальных уравнений |
\begin{equation}\label{syst} | \begin{equation}\label{syst} | ||
\frac{dx}{dt} = f(t, x), | \frac{dx}{dt} = f(t, x), | ||
\end{equation} | \end{equation} | ||
| − | где | + | где |
| − | \begin{equation | + | \begin{equation}\label{right_syst_part} |
| − | f(t, x) \in C_{t, x}^{(0, 1)} (\mathcal{I}_t^{+} \times \ | + | f(t, x) \in C_{t, x}^{(0, 1)} (\mathcal{I}_t^{+} \times \mathbb{R}_x^n) \Leftrightarrow |
| − | f(t, x) \in C_t(\mathcal{I}_t^{+}) \; \forall x \in \ | + | \begin{cases} |
| − | f(t, x) \in C_x^1(\ | + | f(t, x) \in C_t(\mathcal{I}_t^{+}) \; \forall x \in \mathbb{R}_x^n, \\ |
| + | f(t, x) \in C_x^1(\mathbb{R}_x^n) \; \forall t \in \mathcal{I}_t^{+}, | ||
\end{cases} | \end{cases} | ||
| − | \end{equation | + | \end{equation} |
Здесь | Здесь | ||
\begin{equation*} | \begin{equation*} | ||
\mathcal{I}_t^{+} = \{ t \ge 0 \}, \\ | \mathcal{I}_t^{+} = \{ t \ge 0 \}, \\ | ||
| − | |||
\end{equation*} | \end{equation*} | ||
| − | Пусть $$x[t] \equiv x(t; t_0, x_0)$$ | + | Пусть $$x[t] \equiv x(t; t_0, x_0)$$ — решение (\ref{syst}) с начальным условием |
\begin{equation}\label{start_cond} | \begin{equation}\label{start_cond} | ||
| − | x(t_0) = x_0 | + | x(t_0) = x_0. |
\end{equation} | \end{equation} | ||
| + | |||
| + | Тогда условия (\ref{right_syst_part}) гарантируют существование и единственность решения $$x[t]$$ задачи Коши (\ref{syst})-(\ref{start_cond}). | ||
== Основные понятия == | == Основные понятия == | ||
| − | Если $$x[t]$$ | + | Если $$x[t]$$ — решение системы (\ref{syst})-(\ref{start_cond}), то |
# $$x[t]$$ '''неограниченно продолжаемо вправо''' (defined in the future), если $$x[t]$$ имеет смысл на промежутке $$[t_0, +\infty), \ t_0 \in \mathcal{I}_t^{+}$$, | # $$x[t]$$ '''неограниченно продолжаемо вправо''' (defined in the future), если $$x[t]$$ имеет смысл на промежутке $$[t_0, +\infty), \ t_0 \in \mathcal{I}_t^{+}$$, | ||
| − | # $$x[t]$$ ''' | + | # $$x[t]$$ имеет '''конечное время определения''' (finite escape time), если $$x[t]$$ определено лишь на конечном промежутке $$t_0 \le t < T < +\infty, \ t_0 \in \mathcal{I}_t^{+}$$. |
== Непродолжаемость вправо решения, имеющего конечное время определения == | == Непродолжаемость вправо решения, имеющего конечное время определения == | ||
| + | |||
| + | '''Замечание.''' В силу непрерывности правой части уравнения (\ref{syst}) и выполнения условий теоремы существования и единственности решения задачи Коши (\ref{syst})-(\ref{start_cond}) система обладает свойством '''интегральной непрерывности''': если $$x[t] \equiv x(t; t_0, x_0)$$ - решение задачи Коши (\ref{syst})-(\ref{start_cond}) при $$a < t < b$$, то $$\forall \ \varepsilon > 0, \ \forall \ [\alpha, \beta] \subset (a, b) \ \exists \ \delta > 0:$$ решение $$y[t] \equiv y(t; \tau_0, y_0)$$ системы (\ref{syst}) при $$\tau_0 \in [\alpha, \beta]$$ и $$\| y(\tau_0) - x(\tau_0) \| < \delta$$ будет иметь смысл при $$\alpha \le t \le \beta$$, причём $$\| y[t] - x[t] \| < \varepsilon$$ для $$t \in [\alpha, \beta]$$ (см. рис. 1). | ||
| + | |||
| + | [[Файл:Figure1.png|мини|справа|Рис.1. Свойство интегральной непрерывности]] | ||
| + | |||
| + | [[Файл:Figure2.png|мини|справа|Рис.2. Иллюстрация к лемме 1]] | ||
=== Лемма 1 === | === Лемма 1 === | ||
| Строка 33: | Строка 41: | ||
''Если решение $$x[t]$$ имеет конечное время определения $$t_0 \le t < T < +\infty$$, то $$\|x(t)\| \rightarrow +\infty$$ при $$t \rightarrow T - 0$$.'' | ''Если решение $$x[t]$$ имеет конечное время определения $$t_0 \le t < T < +\infty$$, то $$\|x(t)\| \rightarrow +\infty$$ при $$t \rightarrow T - 0$$.'' | ||
| − | '''''Доказательство.''''' Пусть $$\|x(t)\| \nrightarrow +\infty \ при \ t \rightarrow T - 0$$. Тогда $$\exists \ t_k \rightarrow T - 0: x(t_k) \rightarrow y \neq \infty \ при \ k \to +\infty $$. Рассмотрим решение $$y[t] \equiv y(t; T, y)$$, которое существует и единственно согласно теореме Коши и определено в некотором интервале $$(T - \alpha, T + \alpha), \ \alpha > 0$$. Тогда при $$t_k > T - \frac{\alpha}{4}$$ имеем | + | '''''Доказательство.''''' Пусть $$\|x(t)\| \nrightarrow +\infty \ при \ t \rightarrow T - 0$$. Тогда $$\exists \ t_k \rightarrow T - 0: x(t_k) \rightarrow y \neq \infty \ при \ k \to +\infty $$. Рассмотрим решение $$y[t] \equiv y(t; T, y)$$ задачи Коши (\ref{syst}) с начальным условием $$y(T) = y$$, которое существует и единственно согласно теореме Коши и определено в некотором интервале $$(T - \alpha, T + \alpha), \ \alpha > 0$$ (см. рис. 2). Тогда при $$t_k > T - \frac{\alpha}{4}$$ имеем |
\begin{equation*} | \begin{equation*} | ||
x(t; t_k, x(t_k)) \equiv x(t; t_0, x_0), \\ | x(t; t_k, x(t_k)) \equiv x(t; t_0, x_0), \\ | ||
| Строка 43: | Строка 51: | ||
== Достаточные условия неограниченной продолжаемости вправо == | == Достаточные условия неограниченной продолжаемости вправо == | ||
| − | + | <big>'''Следствие из леммы 1'''</big> | |
| − | ''Если решение $$x[t] | + | ''Если решение $$x[t]$$ ограничено в своём максимальном промежутке существования $$t_0 \le t < t_0 + T$$, то оно бесконечно продолжаемо вправо, т.е. $$T = +\infty$$.'' |
| − | Рассмотрим дифференциальное | + | Рассмотрим дифференциальное неравенство |
\begin{equation} \label{diff_ineq} | \begin{equation} \label{diff_ineq} | ||
\dot{v} \le G(t, v), \ t \ge t_0, \ t_0 \in \mathcal{I}_t^{+}, | \dot{v} \le G(t, v), \ t \ge t_0, \ t_0 \in \mathcal{I}_t^{+}, | ||
\end{equation} | \end{equation} | ||
| − | где $$G(t, v)$$ | + | где $$G(t, v)$$ — некоторая непрерывная скалярная функция, определённая при $$t \ge t_0$$ и $$v \in \mathbb{R}^1$$, а $$v = v(t)$$ — непрерывная дифференцируемая положительная скалярная функция. |
| − | Будем говорить, что решение $$v(t) \in C^1$$ неравенства (\ref{diff_ineq}) имеет '''конечное время определения''' $$t_0 \le t < T$$, если $$\dot{v}(t) \le G(t, v)$$ при $$t_0 \le t < T$$ | + | Будем говорить, что решение $$v(t) \in C^1$$ неравенства (\ref{diff_ineq}) имеет '''конечное время определения''' $$t_0 \le t < T$$, если |
| + | # $$\dot{v}(t) \le G(t, v)$$ при $$t_0 \le t < T$$, | ||
| + | # $$\| v(t) \| \to +\infty$$ при $$t \to T - 0 $$. | ||
| − | === Теорема | + | === Теорема Ла–Салля === |
''Пусть'' | ''Пусть'' | ||
| − | # $$S_r^c = \{ \| x \| \ge r \} \subset \ | + | # $$S_r^c = \{ \| x \| \ge r \} \subset \mathbb{R}_x^n$$ — внешность сферы радиуса $$r$$, |
# $$V(t, x) \in C_{t, x}^{(1, 1)} (\mathcal{I}_t^{+} \times S_r^c)$$, | # $$V(t, x) \in C_{t, x}^{(1, 1)} (\mathcal{I}_t^{+} \times S_r^c)$$, | ||
# $$V(t, x) \rightrightarrows \infty$$ ''по'' $$t$$ ''при'' $$\| x \| \rightarrow \infty$$, ''равномерно на каждом конечном промежутке'' $$(a, b) \subset \mathcal{I}_t^{+}$$. | # $$V(t, x) \rightrightarrows \infty$$ ''по'' $$t$$ ''при'' $$\| x \| \rightarrow \infty$$, ''равномерно на каждом конечном промежутке'' $$(a, b) \subset \mathcal{I}_t^{+}$$. | ||
| Строка 70: | Строка 80: | ||
\end{equation} | \end{equation} | ||
| − | ''где'' $$G(t, v)$$ '' | + | ''где'' $$G(t, v)$$ '' — непрерывная скалярная функция,'' |
$$\ \ \ \ \ 2) $$ ''соответствующее скалярное неравенство'' (\ref{diff_ineq}) ''не имеет положительных решений'' $$v(t)$$ ''с конечным временем определения, | $$\ \ \ \ \ 2) $$ ''соответствующее скалярное неравенство'' (\ref{diff_ineq}) ''не имеет положительных решений'' $$v(t)$$ ''с конечным временем определения, | ||
| Строка 76: | Строка 86: | ||
''то каждое решение'' $$x = x(t)$$ ''системы'' (\ref{syst}) ''неограниченно продолжимо вправо.'' | ''то каждое решение'' $$x = x(t)$$ ''системы'' (\ref{syst}) ''неограниченно продолжимо вправо.'' | ||
| − | '''''Доказательство.''''' Допустим, что некоторое решение $$x[t]$$ системы (\ref{syst}) имеет конечное время определения $$t_0 \le t < T < \infty$$. Тогда в силу леммы 1 $$\| x(t) \| \to +\infty$$ при $$t \to T - 0$$ и, следовательно, при $$t \in (t_1, T)$$, где $$t_1 > t_0$$, решение $$x(t)$$ целиком будет содержаться в некоторой области $$S_{r_1}^c$$, где $$r_1 > r$$. Кроме того, можно предполагать, что $$V(t, x) > 0$$ при $$(t, x) \in [t_0, T] \times S_{r_1}^c$$. Но тогда на основании неравенства (\ref{diff_ineq_2}) функция $$v(t) = V(t, x(t))$$ является положительным решением скалярного неравенства (\ref{diff_ineq}) с конечным временем определения $$t_0 \le t < T (v( | + | '''''Доказательство.''''' Допустим, что некоторое решение $$x[t]$$ системы (\ref{syst}) имеет конечное время определения $$t_0 \le t < T < +\infty$$. Тогда в силу леммы 1 $$\| x(t) \| \to +\infty$$ при $$t \to T - 0$$ и, следовательно, при $$t \in (t_1, T)$$, где $$t_1 > t_0$$, решение $$x(t)$$ целиком будет содержаться в некоторой области $$S_{r_1}^c$$, где $$r_1 > r$$. Кроме того, можно предполагать, что $$V(t, x) > 0$$ при $$(t, x) \in [t_0, T] \times S_{r_1}^c$$. Но тогда на основании неравенства (\ref{diff_ineq_2}) функция $$v(t) = V(t, x(t))$$ является положительным решением скалярного неравенства (\ref{diff_ineq}) с конечным временем определения $$t_0 \le t < T \ (v(T) = \infty)$$. А это невозможно в силу условия 2 теоремы. $$\blacksquare$$ |
Достаточные условия того, что неравенство (\ref{diff_ineq}) не имеет положительных решений с конечным временем определения, даёт следующее утверждение. | Достаточные условия того, что неравенство (\ref{diff_ineq}) не имеет положительных решений с конечным временем определения, даёт следующее утверждение. | ||
| − | + | <big>'''Следствие из теоремы Ла–Салля'''</big> | |
| − | ''Пусть'' $$G(t, v) = k(t) L(v)$$, ''где'' $$k(t) \ge 0, L(v) > 0$$ '' | + | ''Пусть'' $$G(t, v) = k(t) L(v)$$, ''где'' $$k(t) \ge 0, L(v) > 0$$ '' — скалярные функции, непрерывные при'' $$t \ge t_0, t_0 \in \mathcal{I}_t^{+}$$. |
''Если'' $$\int\limits_{t_0}^{+\infty} \frac{d v}{L(v)} = +\infty$$, | ''Если'' $$\int\limits_{t_0}^{+\infty} \frac{d v}{L(v)} = +\infty$$, | ||
| Строка 88: | Строка 98: | ||
''то неравенство'' (\ref{diff_ineq}) ''не имеет положительных решений'' $$v(t)$$ ''с конечным временем определения.'' | ''то неравенство'' (\ref{diff_ineq}) ''не имеет положительных решений'' $$v(t)$$ ''с конечным временем определения.'' | ||
| − | '''''Доказательство.''''' Пусть $$\exists \ v(t) > 0, \ t_0 \le t < +\infty$$ неравенства | + | '''''Доказательство.''''' Пусть $$\exists \ v(t) > 0, \ t_0 \le t < +\infty$$, — решение неравенства |
\begin{equation}\label{diff_ineq_3} | \begin{equation}\label{diff_ineq_3} | ||
\frac{d v}{d t} \le k(t) L(v), | \frac{d v}{d t} \le k(t) L(v), | ||
| Строка 98: | Строка 108: | ||
\end{equation} | \end{equation} | ||
| − | Отсюда при $$t \to T - 0$$ получаем, что левая часть неравенства (\ref{diff_ineq_4}) стремится к $$+\infty$$, а правая | + | Отсюда при $$t \to T - 0$$ получаем, что левая часть неравенства (\ref{diff_ineq_4}) стремится к $$+\infty$$, а правая — ограничена, что невозможно. Следовательно, каждое положительное решение $$v(t)$$ неравенства (\ref{diff_ineq_3}) |
* или имеет смысл лишь на некотором конечном промежутке $$[t_0, T)$$, причём $$\| v(t) \| \nrightarrow +\infty$$ при $$t \to T - 0$$, | * или имеет смысл лишь на некотором конечном промежутке $$[t_0, T)$$, причём $$\| v(t) \| \nrightarrow +\infty$$ при $$t \to T - 0$$, | ||
| − | * или же оно определено на бесконечном промежутке $$t_0 \le t < +\infty \ \blacksquare$$ | + | * или же оно определено на бесконечном промежутке $$t_0 \le t < +\infty. \ \blacksquare$$ |
== Пример == | == Пример == | ||
| Строка 111: | Строка 121: | ||
где | где | ||
\begin{equation*} | \begin{equation*} | ||
| − | f(t, x) \in C_{t, x}^{(0, 1)}(\mathcal{I}_t^{+} \times \ | + | f(t, x) \in C_{t, x}^{(0, 1)}(\mathcal{I}_t^{+} \times \mathbb{R}_x^n). |
\end{equation*} | \end{equation*} | ||
| − | Если | + | Если выполнен частный случай условий сублинейного роста |
\begin{cases} | \begin{cases} | ||
| − | + | \| f(t, x) \| \le k(t) \| x \|, \ \| x \| \ge r, \\ | |
| − | \| f(t, x) \| \le k(t) \| x \|, \ | ||
| − | \| x \| \ge r, \\ | ||
k(t) \in C(\mathcal{I}_t^{+}), \\ | k(t) \in C(\mathcal{I}_t^{+}), \\ | ||
k(t) \ge 0 \ \forall t \in \mathcal{I}_t^{+} | k(t) \ge 0 \ \forall t \in \mathcal{I}_t^{+} | ||
| − | |||
\end{cases} | \end{cases} | ||
| − | то все решения $$x(t)$$ системы (\ref{example}) неограниченно | + | то все решения $$x(t)$$ системы (\ref{example}) неограниченно продолжаемы вправо. |
Действительно, пусть | Действительно, пусть | ||
\begin{equation*} | \begin{equation*} | ||
| − | V(x) = \| x \|^2 \equiv | + | V(x) = \| x \|^2 \equiv (x, x). |
\end{equation*} | \end{equation*} | ||
Тогда | Тогда | ||
\begin{equation*} | \begin{equation*} | ||
| − | \dot{V}(x) = | + | \dot{V}(x) = (\frac{d x}{d t}, x) + (x, \frac{d x}{d t}) = 2 x^T f(t, x). |
\end{equation*} | \end{equation*} | ||
| Строка 146: | Строка 153: | ||
\end{equation*} | \end{equation*} | ||
| − | в силу следствия из теоремы | + | в силу следствия из теоремы Ла–Салля $$(L(v) = 2 v)$$ не имеет положительных решений с конечным временем определения . Следовательно, на основании теоремы Ла–Салля каждое решение $$x(t)$$ системы (\ref{example}) имеет смысл при $$t_0 \le t < +\infty$$. |
| + | |||
| + | == Список литературы == | ||
| + | |||
| + | * Б.П. Демидович. Лекции по математической теории устойчивости. Издательство "Наука". Москва. 1967. | ||
| + | * Ж. Ла–Салль, С. Лефшец. Исследование устойчивости прямым методом Ляпунова. Издательство "Мир". 1964. | ||
Текущая версия на 13:51, 21 декабря 2021
Будем рассматривать систему обыкновенных дифференциальных уравнений \begin{equation}\label{syst} \frac{dx}{dt} = f(t, x), \end{equation} где \begin{equation}\label{right_syst_part} f(t, x) \in C_{t, x}^{(0, 1)} (\mathcal{I}_t^{+} \times \mathbb{R}_x^n) \Leftrightarrow \begin{cases} f(t, x) \in C_t(\mathcal{I}_t^{+}) \; \forall x \in \mathbb{R}_x^n, \\ f(t, x) \in C_x^1(\mathbb{R}_x^n) \; \forall t \in \mathcal{I}_t^{+}, \end{cases} \end{equation}
Здесь \begin{equation*} \mathcal{I}_t^{+} = \{ t \ge 0 \}, \\ \end{equation*}
Пусть $$x[t] \equiv x(t; t_0, x_0)$$ — решение (\ref{syst}) с начальным условием \begin{equation}\label{start_cond} x(t_0) = x_0. \end{equation}
Тогда условия (\ref{right_syst_part}) гарантируют существование и единственность решения $$x[t]$$ задачи Коши (\ref{syst})-(\ref{start_cond}).
Содержание
Основные понятия
Если $$x[t]$$ — решение системы (\ref{syst})-(\ref{start_cond}), то
- $$x[t]$$ неограниченно продолжаемо вправо (defined in the future), если $$x[t]$$ имеет смысл на промежутке $$[t_0, +\infty), \ t_0 \in \mathcal{I}_t^{+}$$,
- $$x[t]$$ имеет конечное время определения (finite escape time), если $$x[t]$$ определено лишь на конечном промежутке $$t_0 \le t < T < +\infty, \ t_0 \in \mathcal{I}_t^{+}$$.
Непродолжаемость вправо решения, имеющего конечное время определения
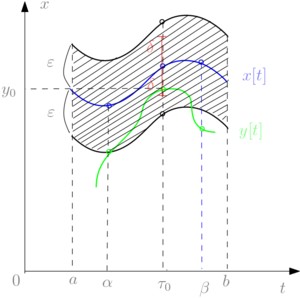
Замечание. В силу непрерывности правой части уравнения (\ref{syst}) и выполнения условий теоремы существования и единственности решения задачи Коши (\ref{syst})-(\ref{start_cond}) система обладает свойством интегральной непрерывности: если $$x[t] \equiv x(t; t_0, x_0)$$ - решение задачи Коши (\ref{syst})-(\ref{start_cond}) при $$a < t < b$$, то $$\forall \ \varepsilon > 0, \ \forall \ [\alpha, \beta] \subset (a, b) \ \exists \ \delta > 0:$$ решение $$y[t] \equiv y(t; \tau_0, y_0)$$ системы (\ref{syst}) при $$\tau_0 \in [\alpha, \beta]$$ и $$\| y(\tau_0) - x(\tau_0) \| < \delta$$ будет иметь смысл при $$\alpha \le t \le \beta$$, причём $$\| y[t] - x[t] \| < \varepsilon$$ для $$t \in [\alpha, \beta]$$ (см. рис. 1).
Лемма 1
Если решение $$x[t]$$ имеет конечное время определения $$t_0 \le t < T < +\infty$$, то $$\|x(t)\| \rightarrow +\infty$$ при $$t \rightarrow T - 0$$.
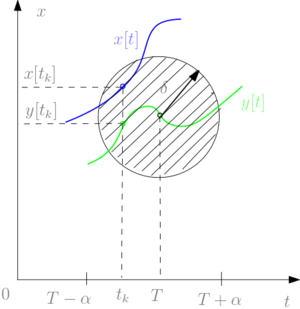
Доказательство. Пусть $$\|x(t)\| \nrightarrow +\infty \ при \ t \rightarrow T - 0$$. Тогда $$\exists \ t_k \rightarrow T - 0: x(t_k) \rightarrow y \neq \infty \ при \ k \to +\infty $$. Рассмотрим решение $$y[t] \equiv y(t; T, y)$$ задачи Коши (\ref{syst}) с начальным условием $$y(T) = y$$, которое существует и единственно согласно теореме Коши и определено в некотором интервале $$(T - \alpha, T + \alpha), \ \alpha > 0$$ (см. рис. 2). Тогда при $$t_k > T - \frac{\alpha}{4}$$ имеем \begin{equation*} x(t; t_k, x(t_k)) \equiv x(t; t_0, x_0), \\ y(t; t_k, y(t_k)) \equiv y(t; T, y). \end{equation*}
Т.к. $$x[t_k]$$ может быть выбрано сколь угодно близко к $$y$$ и $$t_k \to T$$, то при достаточно большом $$k$$ точки $$x[t_k], y[t_k]$$ сколько угодно близки между собой. А тогда на основании свойства интегральной непрерывности получим, что решение $$x(t; t_0, x_0)$$ определено, во всяком случае, на промежутке $$(t_k, t_k + \frac{\alpha}{2}) \supset (T, T + \frac{\alpha}{4})$$. А это противоречит максимальности промежутка $$[t_0, T)$$ существования решения $$x(t)$$ при $$t \ge t_0$$. Таким образом, $$\| x[t] \| \to +\infty$$ при $$t \to T - 0. \ \blacksquare$$
Достаточные условия неограниченной продолжаемости вправо
Следствие из леммы 1
Если решение $$x[t]$$ ограничено в своём максимальном промежутке существования $$t_0 \le t < t_0 + T$$, то оно бесконечно продолжаемо вправо, т.е. $$T = +\infty$$.
Рассмотрим дифференциальное неравенство \begin{equation} \label{diff_ineq} \dot{v} \le G(t, v), \ t \ge t_0, \ t_0 \in \mathcal{I}_t^{+}, \end{equation}
где $$G(t, v)$$ — некоторая непрерывная скалярная функция, определённая при $$t \ge t_0$$ и $$v \in \mathbb{R}^1$$, а $$v = v(t)$$ — непрерывная дифференцируемая положительная скалярная функция.
Будем говорить, что решение $$v(t) \in C^1$$ неравенства (\ref{diff_ineq}) имеет конечное время определения $$t_0 \le t < T$$, если
- $$\dot{v}(t) \le G(t, v)$$ при $$t_0 \le t < T$$,
- $$\| v(t) \| \to +\infty$$ при $$t \to T - 0 $$.
Теорема Ла–Салля
Пусть
- $$S_r^c = \{ \| x \| \ge r \} \subset \mathbb{R}_x^n$$ — внешность сферы радиуса $$r$$,
- $$V(t, x) \in C_{t, x}^{(1, 1)} (\mathcal{I}_t^{+} \times S_r^c)$$,
- $$V(t, x) \rightrightarrows \infty$$ по $$t$$ при $$\| x \| \rightarrow \infty$$, равномерно на каждом конечном промежутке $$(a, b) \subset \mathcal{I}_t^{+}$$.
Тогда, если
$$\ \ \ \ \ 1) \ \frac{\partial V}{\partial t}(t, x)$$ в силу системы (\ref{syst}) при $$t \ge t_0$$ и $$x \in S_r^c$$ удовлетворяет неравенству \begin{equation}\label{diff_ineq_2} \frac{\partial V}{\partial t}(t, x) \le G(t, V(t, x)), \end{equation}
где $$G(t, v)$$ — непрерывная скалярная функция,
$$\ \ \ \ \ 2) $$ соответствующее скалярное неравенство (\ref{diff_ineq}) не имеет положительных решений $$v(t)$$ с конечным временем определения,
то каждое решение $$x = x(t)$$ системы (\ref{syst}) неограниченно продолжимо вправо.
Доказательство. Допустим, что некоторое решение $$x[t]$$ системы (\ref{syst}) имеет конечное время определения $$t_0 \le t < T < +\infty$$. Тогда в силу леммы 1 $$\| x(t) \| \to +\infty$$ при $$t \to T - 0$$ и, следовательно, при $$t \in (t_1, T)$$, где $$t_1 > t_0$$, решение $$x(t)$$ целиком будет содержаться в некоторой области $$S_{r_1}^c$$, где $$r_1 > r$$. Кроме того, можно предполагать, что $$V(t, x) > 0$$ при $$(t, x) \in [t_0, T] \times S_{r_1}^c$$. Но тогда на основании неравенства (\ref{diff_ineq_2}) функция $$v(t) = V(t, x(t))$$ является положительным решением скалярного неравенства (\ref{diff_ineq}) с конечным временем определения $$t_0 \le t < T \ (v(T) = \infty)$$. А это невозможно в силу условия 2 теоремы. $$\blacksquare$$
Достаточные условия того, что неравенство (\ref{diff_ineq}) не имеет положительных решений с конечным временем определения, даёт следующее утверждение.
Следствие из теоремы Ла–Салля
Пусть $$G(t, v) = k(t) L(v)$$, где $$k(t) \ge 0, L(v) > 0$$ — скалярные функции, непрерывные при $$t \ge t_0, t_0 \in \mathcal{I}_t^{+}$$.
Если $$\int\limits_{t_0}^{+\infty} \frac{d v}{L(v)} = +\infty$$,
то неравенство (\ref{diff_ineq}) не имеет положительных решений $$v(t)$$ с конечным временем определения.
Доказательство. Пусть $$\exists \ v(t) > 0, \ t_0 \le t < +\infty$$, — решение неравенства \begin{equation}\label{diff_ineq_3} \frac{d v}{d t} \le k(t) L(v), \end{equation}
такое, что $$\| v(T) \| = +\infty$$. Тогда \begin{equation}\label{diff_ineq_4} \int\limits_{v(t_0)}^{v(t)} \frac{d v}{L(v)} \le \int\limits_{t_0}^{t} k(\tau) d\tau. \end{equation}
Отсюда при $$t \to T - 0$$ получаем, что левая часть неравенства (\ref{diff_ineq_4}) стремится к $$+\infty$$, а правая — ограничена, что невозможно. Следовательно, каждое положительное решение $$v(t)$$ неравенства (\ref{diff_ineq_3})
- или имеет смысл лишь на некотором конечном промежутке $$[t_0, T)$$, причём $$\| v(t) \| \nrightarrow +\infty$$ при $$t \to T - 0$$,
- или же оно определено на бесконечном промежутке $$t_0 \le t < +\infty. \ \blacksquare$$
Пример
Рассмотрим действительную систему \begin{equation}\label{example} \frac{d x}{d t} = f(t, x), \end{equation}
где \begin{equation*} f(t, x) \in C_{t, x}^{(0, 1)}(\mathcal{I}_t^{+} \times \mathbb{R}_x^n). \end{equation*}
Если выполнен частный случай условий сублинейного роста \begin{cases} \| f(t, x) \| \le k(t) \| x \|, \ \| x \| \ge r, \\ k(t) \in C(\mathcal{I}_t^{+}), \\ k(t) \ge 0 \ \forall t \in \mathcal{I}_t^{+} \end{cases}
то все решения $$x(t)$$ системы (\ref{example}) неограниченно продолжаемы вправо.
Действительно, пусть \begin{equation*} V(x) = \| x \|^2 \equiv (x, x). \end{equation*}
Тогда \begin{equation*} \dot{V}(x) = (\frac{d x}{d t}, x) + (x, \frac{d x}{d t}) = 2 x^T f(t, x). \end{equation*}
Используя неравенство Коши, получим \begin{equation*} \dot{V}(x) \le 2 \| x^T \| \| f(t, x) \| \le 2 k(t) V(x) \equiv G(t, V(x)) \end{equation*}
при $$t \ge t_0$$ и $$\| x \| \ge r$$. Но неравенство \begin{equation*} \dot{v}(t) \le 2 k(t) v(t) \end{equation*}
в силу следствия из теоремы Ла–Салля $$(L(v) = 2 v)$$ не имеет положительных решений с конечным временем определения . Следовательно, на основании теоремы Ла–Салля каждое решение $$x(t)$$ системы (\ref{example}) имеет смысл при $$t_0 \le t < +\infty$$.
Список литературы
- Б.П. Демидович. Лекции по математической теории устойчивости. Издательство "Наука". Москва. 1967.
- Ж. Ла–Салль, С. Лефшец. Исследование устойчивости прямым методом Ляпунова. Издательство "Мир". 1964.