Задача о тележке: различия между версиями
Alexei (обсуждение | вклад) |
Alexei (обсуждение | вклад) |
||
| (не показано 45 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | + | ||
| − | + | == Постановка задачи == | |
Рассмотрим задачу движение тележки. | Рассмотрим задачу движение тележки. | ||
| + | [[Файл:11.png|мини]] | ||
В движение тележку приводит тяга двигателя <math>F_{\textbf{вн}}</math>,ей будет препятствовать вязкое трение <math>F_{\textbf{тр}}= -k \dot{x}</math> и сопротивление среды <math>F_{сопр}=-d\dot{x}^2</math>. <br /> | В движение тележку приводит тяга двигателя <math>F_{\textbf{вн}}</math>,ей будет препятствовать вязкое трение <math>F_{\textbf{тр}}= -k \dot{x}</math> и сопротивление среды <math>F_{сопр}=-d\dot{x}^2</math>. <br /> | ||
По второму закону Ньютона:<br /> | По второму закону Ньютона:<br /> | ||
| Строка 19: | Строка 20: | ||
$$ | $$ | ||
</center> | </center> | ||
| − | Добавляем | + | Добавляем граничные условия: |
<center> | <center> | ||
$$ | $$ | ||
| Строка 35: | Строка 36: | ||
$$ | $$ | ||
</center> | </center> | ||
| − | То есть мы хотим минимизировать наши | + | То есть мы хотим минимизировать наши усилия при этом передвинув тележку из точки 0 в точку с координатой L.<br /> |
Как итог получаем систему: | Как итог получаем систему: | ||
<center> | <center> | ||
| Строка 49: | Строка 50: | ||
$$ | $$ | ||
</center> | </center> | ||
| − | + | ||
| − | Выпишем ПМП(Принцип максимума Понтрягина) для рассматриваемой задачи.<br /> | + | == Принцип максимума Понтрягина == |
| + | Выпишем ПМП([https://sawiki.cs.msu.ru/index.php/%D0%9F%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF_%D0%BC%D0%B0%D0%BA%D1%81%D0%B8%D0%BC%D1%83%D0%BC%D0%B0_%D0%9B.%D0%A1._%D0%9F%D0%BE%D0%BD%D1%82%D1%80%D1%8F%D0%B3%D0%B8%D0%BD%D0%B0_%D0%B4%D0%BB%D1%8F_%D0%BE%D0%B1%D1%89%D0%B5%D0%B9_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8_%D0%BE%D0%BF%D1%82%D0%B8%D0%BC%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B3%D0%BE_%D1%83%D0%BF%D1%80%D0%B0%D0%B2%D0%BB%D0%B5%D0%BD%D0%B8%D1%8F Принцип максимума Понтрягина]) для рассматриваемой задачи.<br /> | ||
Первым шагом сделаем замену переменных: | Первым шагом сделаем замену переменных: | ||
<center> | <center> | ||
| Строка 67: | Строка 69: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Функция Гамильтона-Понтрягина примет вид: | + | Функция Гамильтона $$-$$ Понтрягина примет вид: |
<center> | <center> | ||
<math> | <math> | ||
| Строка 73: | Строка 75: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Учитывая все | + | Учитывая все вышесказанное, ПМП примет вид: |
| − | Пусть $$ \{ x^*(\cdot), u^*(\cdot) \}$$ - оптимальная пара.<br /> | + | Пусть $$ \{ x^*(\cdot), u^*(\cdot) \}$$ $$-$$ оптимальная пара.<br /> |
Тогда $$ \exists \tilde{\psi}:[t_0^*,t_1^*] \rightarrow \mathcal{R}^{n+1}$$ такая что:<br /> | Тогда $$ \exists \tilde{\psi}:[t_0^*,t_1^*] \rightarrow \mathcal{R}^{n+1}$$ такая что:<br /> | ||
(УН) $$\quad 1) \quad \psi^*(t) \neq 0 , \quad t \in [0,T], $$ <br /> | (УН) $$\quad 1) \quad \psi^*(t) \neq 0 , \quad t \in [0,T], $$ <br /> | ||
| Строка 126: | Строка 128: | ||
</center> | </center> | ||
| − | + | ==Нормальный случай == | |
Пусть $$\psi_0 \equiv \psi_0^0<0 $$,положим $$\psi_0 = -1 $$. Тогда из (УМ): | Пусть $$\psi_0 \equiv \psi_0^0<0 $$,положим $$\psi_0 = -1 $$. Тогда из (УМ): | ||
<center> | <center> | ||
| Строка 137: | Строка 139: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | === Движение при $$\psi_2^0>1$$ === | |
| − | + | ====Движение в окрестности нуля==== | |
Начало движение из нуля, мы начнем разгоняться и в какой то довольно маленькой окрестности $$ u_3^* = u_3^{max}$$ <br /> | Начало движение из нуля, мы начнем разгоняться и в какой то довольно маленькой окрестности $$ u_3^* = u_3^{max}$$ <br /> | ||
В этой окрестности:<br /> | В этой окрестности:<br /> | ||
| Строка 162: | Строка 164: | ||
<math> | <math> | ||
\begin{cases} | \begin{cases} | ||
| − | + | x_2(0) = 0 \\ | |
| − | \ | + | \psi_2(0) = \psi_2^0 >1 \\ |
\end{cases} | \end{cases} | ||
</math> | </math> | ||
</center> | </center> | ||
| − | В этой системе | + | В этой системе нас будут интересовать второе и четвёртое уравнение, поскольку только значения $$x_2$$ и $$\psi_2$$ влияют на выбранное управление, соответственно, могут привести к переключению. До тех пор, пока переключение не |
| + | произошло, движение описываться указанной системой. Понимая это, начальные условия на $$x_1$$ и $$\psi_1$$ мы сразу опустили.<br /> | ||
Тогда система примет вид: | Тогда система примет вид: | ||
<center> | <center> | ||
| Строка 178: | Строка 181: | ||
</center> | </center> | ||
Посмотрим как будут вести себя траектории, на картинке схематично изображены варианты траекторий: | Посмотрим как будут вести себя траектории, на картинке схематично изображены варианты траекторий: | ||
| − | [[Файл: | + | [[Файл:22.png|обрамить|центр]] |
| − | + | ===== Рассмотрим 2-ую траекторию===== | |
Хотим доказать невозможность такой траектории. Ищем особые точки для $$x_2$$: | Хотим доказать невозможность такой траектории. Ищем особые точки для $$x_2$$: | ||
<center> | <center> | ||
| Строка 192: | Строка 195: | ||
</center> | </center> | ||
Таким образом в $$ x_2^+$$ находится аттрактор к которому будут стремится траектории системы. Следовательно вторая траектория невозможна. | Таким образом в $$ x_2^+$$ находится аттрактор к которому будут стремится траектории системы. Следовательно вторая траектория невозможна. | ||
| − | + | ===== Рассмотрим 3-ую траекторию===== | |
Докажем, что такой вид траектории также невозможен. <br /> | Докажем, что такой вид траектории также невозможен. <br /> | ||
Пусть $$ \dot{\psi}_2 > 0$$ из уравнения : | Пусть $$ \dot{\psi}_2 > 0$$ из уравнения : | ||
| Строка 212: | Строка 215: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Следовательно $$ x_2$$ и $$\psi_2$$ бесконечно | + | Следовательно $$ x_2$$ и $$\psi_2$$ бесконечно возрастает. Следовательно $$x_2(T) = \varepsilon$$ не выполняется. <br /> |
| − | + | противоречие. | |
| − | + | ||
| + | ===== Рассмотрим 1-ую траекторию===== | ||
Таким образом имеет смысл рассматриваем пары $$(\psi_1^0,\psi_2^0)$$ и $$\exists \tau \quad \psi_2(\tau) = 1 $$, то есть имеет место переключение. | Таким образом имеет смысл рассматриваем пары $$(\psi_1^0,\psi_2^0)$$ и $$\exists \tau \quad \psi_2(\tau) = 1 $$, то есть имеет место переключение. | ||
| − | + | ====Особый режим после $$\tau_1 $$ ==== | |
Режим будет особый, если $$t \in [\tau_1,\tau_1 + \delta)$$ выполнялось $$\psi_2(t) = 1$$ <br /> | Режим будет особый, если $$t \in [\tau_1,\tau_1 + \delta)$$ выполнялось $$\psi_2(t) = 1$$ <br /> | ||
Тогда получаем:<br /> | Тогда получаем:<br /> | ||
| Строка 240: | Строка 244: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | ===== Движение непосредственно после особого режима ===== | |
Рассмотрим движение непосредственно после выхода из особого режима, пусть $$\tau_2$$ - выход из особого режима: | Рассмотрим движение непосредственно после выхода из особого режима, пусть $$\tau_2$$ - выход из особого режима: | ||
* $$u_3(\tau_2 + 0)> u_3^{ос}$$. В этом случаи $$\psi_2(t)>1 \Rightarrow u_3 = u_3^{max} \Rightarrow x_2 \uparrow, \psi_2 \uparrow \Rightarrow$$ не сможем вернуться в $$ x_2 = \varepsilon$$(тоже так же как для 3 траектории) | * $$u_3(\tau_2 + 0)> u_3^{ос}$$. В этом случаи $$\psi_2(t)>1 \Rightarrow u_3 = u_3^{max} \Rightarrow x_2 \uparrow, \psi_2 \uparrow \Rightarrow$$ не сможем вернуться в $$ x_2 = \varepsilon$$(тоже так же как для 3 траектории) | ||
* $$u_3(\tau_2 + 0) < u_3^{ос} \Rightarrow \psi_2(t)<1 \Rightarrow u_3^*=0, x_2 \downarrow, \psi_2 \downarrow $$ | * $$u_3(\tau_2 + 0) < u_3^{ос} \Rightarrow \psi_2(t)<1 \Rightarrow u_3^*=0, x_2 \downarrow, \psi_2 \downarrow $$ | ||
| − | + | ===== Движение при $$t> \tau_2 $$ ===== | |
Как мы выяснили $$u_3^* =0$$ из чего наша система принимает вид: | Как мы выяснили $$u_3^* =0$$ из чего наша система принимает вид: | ||
<center> | <center> | ||
| Строка 255: | Строка 259: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Начальное | + | Начальное условие для этого участка движения выглядит следующим образом: |
<center> | <center> | ||
<math> | <math> | ||
| Строка 264: | Строка 268: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | ===== | + | |
| + | =====Переключение по $$x_2$$===== | ||
Пусть $$ \exists \tau_3 >\tau_2: x_2(\tau_3) = 0.$$ Решая задачу в обратном порядке, получаем: | Пусть $$ \exists \tau_3 >\tau_2: x_2(\tau_3) = 0.$$ Решая задачу в обратном порядке, получаем: | ||
<center> | <center> | ||
| Строка 276: | Строка 281: | ||
в силу единственности задачи Коши получаем единственную траекторию $$ x \equiv 0 $$, что противоречит $$x_2(\tau_2)$$ | в силу единственности задачи Коши получаем единственную траекторию $$ x \equiv 0 $$, что противоречит $$x_2(\tau_2)$$ | ||
| − | ===== | + | ===== Переключение по $$\psi_2$$ ===== |
Пусть $$ \exists \tau_3 :\psi_2(\tau_3)=0$$ - время переключение определяется в силу единственности решения задачи Коши.<br /> | Пусть $$ \exists \tau_3 :\psi_2(\tau_3)=0$$ - время переключение определяется в силу единственности решения задачи Коши.<br /> | ||
Если $$\psi_2 \neq 0 \forall t \in[0,T) $$, полагаем $$\tau_3=T $$<br /> | Если $$\psi_2 \neq 0 \forall t \in[0,T) $$, полагаем $$\tau_3=T $$<br /> | ||
| Строка 292: | Строка 297: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Получили | + | Получили противоречие. Особого режима нету.<br /> |
В окресности $$\psi_2 = 0 $$ | В окресности $$\psi_2 = 0 $$ | ||
<center> | <center> | ||
| Строка 320: | Строка 325: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | + | ||
| + | ====Без особого режима после $$\tau_1 $$ ==== | ||
Движение на $$t >\tau_1 $$ определятся системой: | Движение на $$t >\tau_1 $$ определятся системой: | ||
<center> | <center> | ||
| Строка 350: | Строка 356: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | === Движение при $$\psi_2^0<1$$ === | ||
| + | Выпишем ОДУ для движение тележки, поскольку в силу (УМ) $$u_3^*(0+)=0 $$ | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{cases} | ||
| + | \dot{x}_1=x_2 \\ | ||
| + | \dot{x}_2 = -(u_1+u_2x_2)x_2 \\ | ||
| + | \dot{\psi}_1 = 0 \\ | ||
| + | \dot{\psi}_2 = -\psi_1^0+\psi_2(u_1+2u_2x_2)\\ | ||
| + | x_2(0)=0 \\ | ||
| + | \end{cases} | ||
| + | </math> | ||
| + | </center> | ||
| + | В силу единственности, для этой системы $$x_2 \equiv 0 $$ $$-$$ единственное решение.<br /> | ||
| + | Следовательно, движение $$\tau_{\textbf{нач}} $$ начнется тогда, когда $$u_3>0 $$, то есть будет $$\psi_2 \geq 1 $$ учитывая непрерывность : | ||
| + | <center> | ||
| + | <math> | ||
| + | \psi_2(\tau_\textbf{нач})=1, \quad \psi_2(t) > 1 \quad t \in (\tau_\textbf{нач},\tau_\textbf{нач} +\delta) | ||
| + | </math> | ||
| + | </center> | ||
| + | В этот момент произойдёт переключение по остальным компонентам управления, и начнётся движение: | ||
| + | <center> | ||
| + | <math> | ||
| + | u_1^* = u_1^{max},u_2^* = u_1^{min} \quad t > \tau_{\textbf{нач}} | ||
| + | </math> | ||
| + | </center> | ||
| + | Из рассмотренного случая при $$\psi_2>1$$, имеем ровно одно переключение. То есть , если $$x_2(t) > \varepsilon$$ - то не будет достигнуто краевое условие, из единственности решения задачи Коши. | ||
| + | [[Файл:33.png|мини|центр]] | ||
| + | Учитывая начальное условие: | ||
| + | <center> | ||
| + | <math> | ||
| + | L > T \varepsilon | ||
| + | </math> | ||
| + | </center> | ||
| + | Площадь криволинейной трапеции меньше площади прямоугольника: | ||
| + | <center> | ||
| + | <math> | ||
| + | L = \int\limits_0^T x_2(\tau) d \tau \leq \varepsilon (T - \tau_{\textbf{нач}}) <T \varepsilon | ||
| + | </math> | ||
| + | </center> | ||
| + | Случай невозможен. Получили противоречие с краевыми условиями. | ||
| + | |||
| + | === Движение при $$\psi_2^0=1$$ === | ||
| + | Данный случай полностью повторяет предыдущий пункт, однако теперь | ||
| + | возможен вариант $$\tau_{\textbf{нач}} = 0$$. <br /> | ||
| + | Так или иначе, условие $$L > T \varepsilon $$ всё ещё делает | ||
| + | этот случай невозможным. | ||
| − | + | ==Анормальный случай == | |
<center> | <center> | ||
<math> | <math> | ||
| Строка 357: | Строка 410: | ||
</math> | </math> | ||
</center> | </center> | ||
| − | Отличие в u_2^*: | + | Отличие в $$u_2^*$$: |
<center> | <center> | ||
<math> | <math> | ||
| Строка 368: | Строка 421: | ||
</center> | </center> | ||
Остальные компоненты управления остаются такими же: | Остальные компоненты управления остаются такими же: | ||
| − | |||
<math> | <math> | ||
u_1^*= \begin{cases} | u_1^*= \begin{cases} | ||
| Строка 381: | Строка 433: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
| + | Пусть $$ \psi_2^0 >0$$. Предположим что при переходе через $$\psi_2=0 $$ возможен особый режим | ||
| + | <center> | ||
| + | <math> | ||
| + | 0 = \dot{\psi}_2 = - \psi_1^0 + 0\cdot (...) \Rightarrow \psi_1^0=0 \Rightarrow (\psi_0,\psi_1,\psi_2)=0 | ||
| + | </math> | ||
| + | </center> | ||
| + | Это происходит на отрезке ненулевой меры , получаем противоречие (УН). <br /> | ||
| + | То есть особый режим невозможен, происходит простое переключение по всем трем компонентам. <br /> | ||
| + | Перепараметризуем, переходим к параметру $$\tau_1: \psi_2(\tau_1) = 0.$$ <br /> | ||
| + | Поскольку при этом $$\psi(\tau_1) \neq 0$$, то $$\psi_1(\tau_1) \neq 0$$. <br /> | ||
| + | Нормируем начальный момент времени: $$\psi_1(\tau_1) =1 $$ <br /> | ||
| + | Случай $$\psi_1(\tau_1) = -1 $$ исключаем, по доказанному ранее это влечёт $$\psi_2 \uparrow$$ и торможения не будет.<br /> | ||
| + | Зафиксировав $$\psi_0^0, \psi_1^0 $$ и перейдя к перебору по $$ \tau_1$$, получаем | ||
| + | однопараметрическое семейство решений. | ||
Текущая версия на 17:21, 11 декабря 2021
Содержание
- 1 Постановка задачи
- 2 Принцип максимума Понтрягина
- 3 Нормальный случай
- 4 Анормальный случай
Постановка задачи
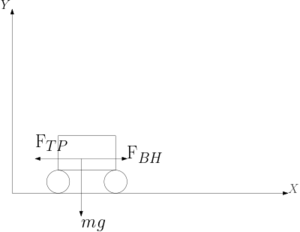
Рассмотрим задачу движение тележки.
В движение тележку приводит тяга двигателя \(F_{\textbf{вн}}\),ей будет препятствовать вязкое трение \(F_{\textbf{тр}}= -k \dot{x}\) и сопротивление среды \(F_{сопр}=-d\dot{x}^2\).
По второму закону Ньютона:
Обозначая $$ \dfrac{k}{m} = u_1 \in [u_1^{min},u_1^{max}], \frac{d}{m} = u_2 \in [u_2^{min},u_2^{max}],\dfrac{F_{\textbf{вн}}}{m} = u_3 \in [0,u_3^{max}]$$, и приводя к нормальному виду
получим следующую систему:
Добавляем граничные условия:
$$ t_0 = 0, \\ x_1(0) = x_2(0) = 0,\\ t_1= T\\ x_1(T) = L\\ x_2(t) = \varepsilon $$
Наша цель минимизировать функционал:
$$ J = \int\limits_0^T u_3(t)dt \rightarrow \inf\limits_{u(\cdot)} $$
То есть мы хотим минимизировать наши усилия при этом передвинув тележку из точки 0 в точку с координатой L.
Как итог получаем систему:
$$ \dot{x}_1 = x_2, \\ \dot{x}_2= -(u_1x_2+u_2x_2^2)+u_3\\ \quad u_1 \in [u_1^{min}, u_1^{max}],\quad 0<u_1^{min}<u_1^{max}\\ \quad u_2 \in [u_2^{min}, u_2^{max}],\quad 0<u_2^{min}<u_2^{max} \\ \quad u_3 \in [0,u_3^{max}],\quad 0 < u_3^{max} \\ \quad t_0 = 0, \quad x_1(0) = x_2(0) = 0 \\ \quad t_1 = T > 0, \quad x_1(T) = L, \quad x_2(T) = \varepsilon >0, \quad L > T \varepsilon \\ J = \int\limits_0^T u_3(t)dt \rightarrow \inf\limits_{u(\cdot)} $$
Принцип максимума Понтрягина
Выпишем ПМП(Принцип максимума Понтрягина) для рассматриваемой задачи.
Первым шагом сделаем замену переменных:
\( x_0 = \int\limits_0^T u_3(t)dt \rightarrow \inf\limits_{u(\cdot)} \)
Тогда наша система примет вид:
\( \begin{cases} \dot{x}_0 = u_3,\\ \dot{x}_1 = x_2, \\ \dot{x}_2= -(u_1x_2+u_2x_2^2)+u_3\\ \end{cases} \)
Функция Гамильтона $$-$$ Понтрягина примет вид:
\( \mathscr{H} = \psi_0u_3 + \psi_1x_2 + \psi_2(u_3 - u_1x_2-u_2x_2^2) \)
Учитывая все вышесказанное, ПМП примет вид:
Пусть $$ \{ x^*(\cdot), u^*(\cdot) \}$$ $$-$$ оптимальная пара.
Тогда $$ \exists \tilde{\psi}:[t_0^*,t_1^*] \rightarrow \mathcal{R}^{n+1}$$ такая что:
(УН) $$\quad 1) \quad \psi^*(t) \neq 0 , \quad t \in [0,T], $$
(CC) $$ \quad 2)$$
\( \begin{cases} \dot{\psi}_0^* = - \dfrac{\partial \mathscr{H}}{\partial x_0} = 0\\ \dot{\psi}_1^* = - \dfrac{\partial \mathscr{H}}{\partial x_1} = 0\\ \dot{\psi}_2^* = - \dfrac{\partial \mathscr{H}}{\partial x_2} = - \psi_1^{0,*}+ \psi_2^*(u_1^*+2u_2^*x_2^*)\\ \end{cases} \)
(УМ) $$ \quad 3) \quad\mathscr{H}(\tilde{\psi}^*(t),\tilde{x}^*(t),\tilde{u}^*(t)) = \sup \limits_{u} \mathscr{H}(\tilde{\psi}^*(t),\tilde{x}^*(t),u)$$ для п.в. $$ t \in [0,T]$$
$$ \quad \quad \quad 4) $$
\( \psi_0^*(\cdot) \equiv const \leq 0,\\ \mathscr{M}(\tilde{\psi}^*(t),\tilde{x}^*(t)) \equiv const = 0 \)
Из УМ(Условие максимума) получаем:
\( u_1^* = \begin{cases} u_1^{min}, & \psi_2x_2 >0 \\ [u_1^{min},u_1^{max}], & \psi_2x_2 = 0 \\ u_1^{max},& \psi_2x_2 <0 \end{cases} \)
\( u_2^* = \begin{cases} u_2^{min}, & \psi_2 >0, x_2 \neq 0\\ [u_2^{min},u_2^{max}], & \psi_2 x_2 = 0\\ u_2^{max}, & \psi_2 <0 ,x_2 \neq 0 \end{cases} \)
\( u_3^* = \begin{cases} u_3^{max}, & \psi_0^0+\psi_2 >0 \\ [0,u_3^{max}], & \psi_0^0+\psi_2 = 0\\ u_2^{max}, & \psi_0^0+\psi_2 < 0 \end{cases} \)
Нормальный случай
Пусть $$\psi_0 \equiv \psi_0^0<0 $$,положим $$\psi_0 = -1 $$. Тогда из (УМ):
\( u_3^* = \begin{cases} u_3^{max}, & \psi_2 > 1\\ [0,u_3^{max}], & \psi_2 = 1 \\ 0 , & \psi_2 <1 \end{cases} \)
Движение при $$\psi_2^0>1$$
Движение в окрестности нуля
Начало движение из нуля, мы начнем разгоняться и в какой то довольно маленькой окрестности $$ u_3^* = u_3^{max}$$
В этой окрестности:
\( \dot{x}_2 = u_3^{max} - (u_1 + u_2x_2)x_2 \)
В этой малой окрестности $$x_2 \approx 0, u_3^{max}>0 ,$$ то есть $$\dot{x}_2 > 0 .$$
В начале будет происходить ускорение и вся динамика будет описываться:
\( \begin{cases} \dot{x}_1 = x_2 \\ \dot{x}_2 = u_3^{max} - (u_1^{min}+ u_2^{min}x_2)x_2 \\ \dot{\psi}_1 = 0\\ \dot{\psi}_2 = - \psi_1 +\psi_2(u_1^{min}+2u_2^{min}x_2) \end{cases} \)
с начальными условиями:
\( \begin{cases} x_2(0) = 0 \\ \psi_2(0) = \psi_2^0 >1 \\ \end{cases} \)
В этой системе нас будут интересовать второе и четвёртое уравнение, поскольку только значения $$x_2$$ и $$\psi_2$$ влияют на выбранное управление, соответственно, могут привести к переключению. До тех пор, пока переключение не
произошло, движение описываться указанной системой. Понимая это, начальные условия на $$x_1$$ и $$\psi_1$$ мы сразу опустили.
Тогда система примет вид:
\( \begin{cases} \dot{x}_2 = u_3^{max} - (u_1^{min}+ u_2^{min}x_2)x_2 \\ \dot{\psi}_2 = - \psi_1 +\psi_2(u_1^{min}+2u_2^{min}x_2) \end{cases} \)
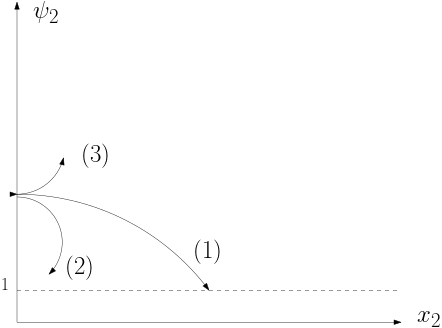
Посмотрим как будут вести себя траектории, на картинке схематично изображены варианты траекторий:
Рассмотрим 2-ую траекторию
Хотим доказать невозможность такой траектории. Ищем особые точки для $$x_2$$:
\( \dot{x}_2 = 0 \Leftrightarrow u_2^{min}x_2^2+u_1^{min}x_2-u_3^{max} = 0 \)
\( x_2 = \dfrac{-u_1^{min} \pm \sqrt{D}}{2u_2^{min}} \)
Таким образом в $$ x_2^+$$ находится аттрактор к которому будут стремится траектории системы. Следовательно вторая траектория невозможна.
Рассмотрим 3-ую траекторию
Докажем, что такой вид траектории также невозможен.
Пусть $$ \dot{\psi}_2 > 0$$ из уравнения :
\( \dot{\psi}_2 = - \psi_1^0 + \psi_2 u_1^{min} \)
Такое возможно при:
\( \psi_1^0 < \psi_2u_1^{min} \)
Поскольку $$\psi_2$$ возрастает по нашему предположению, тогда наше условие будет выполнено всегда, если:
\( \psi_1^0 < \psi_2^0u_1^{min} \)
Следовательно $$ x_2$$ и $$\psi_2$$ бесконечно возрастает. Следовательно $$x_2(T) = \varepsilon$$ не выполняется.
противоречие.
Рассмотрим 1-ую траекторию
Таким образом имеет смысл рассматриваем пары $$(\psi_1^0,\psi_2^0)$$ и $$\exists \tau \quad \psi_2(\tau) = 1 $$, то есть имеет место переключение.
Особый режим после $$\tau_1 $$
Режим будет особый, если $$t \in [\tau_1,\tau_1 + \delta)$$ выполнялось $$\psi_2(t) = 1$$
Тогда получаем:
$$ \dot{\psi}_2(t) = 0 \Rightarrow -\psi_1^0+\psi_2(t)(u_1^{min}+2u_2^{min}x_2) = -\psi_1^0+1(u_1^{min}+2u_2^{min}x_2) = 0$$
Что эквивалентно:
\( x_2 = \dfrac{\psi_1^0-u_1^{min}}{2u_2^{min}} \)
Из $$x_2>0 $$ получаем ограничение $$ \psi_1^0 - u_1^{min} > 0.$$ Если это условие не выполнено, особый режим невозможен. Попадая в особый режим, получаем:
\( 0 = u_3-(u_1^{min}+u_2^{min}x_2^{oc})x_2^{ос} = \{\textbf{по определению}\} = x_2^{ос} \)
Из чего следует:
\( u_3^{ос}=(u_1^{min}+u_2^{min}x_2^{oc})x_2^{ос} \)
Движение непосредственно после особого режима
Рассмотрим движение непосредственно после выхода из особого режима, пусть $$\tau_2$$ - выход из особого режима:
- $$u_3(\tau_2 + 0)> u_3^{ос}$$. В этом случаи $$\psi_2(t)>1 \Rightarrow u_3 = u_3^{max} \Rightarrow x_2 \uparrow, \psi_2 \uparrow \Rightarrow$$ не сможем вернуться в $$ x_2 = \varepsilon$$(тоже так же как для 3 траектории)
- $$u_3(\tau_2 + 0) < u_3^{ос} \Rightarrow \psi_2(t)<1 \Rightarrow u_3^*=0, x_2 \downarrow, \psi_2 \downarrow $$
Движение при $$t> \tau_2 $$
Как мы выяснили $$u_3^* =0$$ из чего наша система принимает вид:
\( \begin{cases} \dot{x}_2 = -(u_1^{min} +u_2^{min}x_2)x_2\\ \dot{\psi}_2 = -\psi_1 + \psi_2(u_1^{min}+2u_2^{min}x_2) \end{cases} \)
Начальное условие для этого участка движения выглядит следующим образом:
\( \begin{cases} x_2(\tau_1) = x_2(\tau_2)=\varepsilon\\ \psi_2(\tau_2)=1 \end{cases} \)
Переключение по $$x_2$$
Пусть $$ \exists \tau_3 >\tau_2: x_2(\tau_3) = 0.$$ Решая задачу в обратном порядке, получаем:
\( \begin{cases} \dot{x}_2 = -(u_1^{min}+u_2^{min}x_2)x_2\\ x_2(\tau_3) = 0 \end{cases} \)
в силу единственности задачи Коши получаем единственную траекторию $$ x \equiv 0 $$, что противоречит $$x_2(\tau_2)$$
Переключение по $$\psi_2$$
Пусть $$ \exists \tau_3 :\psi_2(\tau_3)=0$$ - время переключение определяется в силу единственности решения задачи Коши.
Если $$\psi_2 \neq 0 \forall t \in[0,T) $$, полагаем $$\tau_3=T $$
После указанного переключения $$u_3^*=0$$
Проверяем на особый режим. Если он возможен:
\( 0 = \dot{\psi}_2 = - \psi_1^0 + \psi_2(u_1+2u_2x_2)= -\psi_1^0 \)
Но по условию из первого подключения
\( \psi_1^0 = u_1^{min}+2u_2^{min}x_2(\tau_1)>0 \)
Получили противоречие. Особого режима нету.
В окресности $$\psi_2 = 0 $$
\( \dot{\psi}_2= -\psi_1^0+\psi_2(u_1+2u_2x_2)<0 \)
В достаточно малой окрестности первое слагаемое отрицательно, а второе приблизительно равно нулю.
Следовательно при $$\psi_2=0$$ траектория пойдет вниз, произойдет переключение по все компонентам.
\( \begin{cases} u_1^*=u_1^{max},\\ u_2^*=u_2^{max},\\ u_3^* = 0 \end{cases} \)
Мы начинаем тормозить.
При этом система приобретает вид:
\( \begin{cases} \dot{x}_2 = -(u_1^{max}+u_2^{max}x_2)x_2\\ \dot{\psi}_2= -\psi_1^0 + \psi_2(u_1^{max}+2u_2^{max}x_2) \end{cases} \)
Без особого режима после $$\tau_1 $$
Движение на $$t >\tau_1 $$ определятся системой:
\( \begin{cases} \dot{x}_2 = u_3-(u_1^{min}+u_2^{min}x_2)x_2\\ \dot{\psi}_2 = - \psi_1^0+\psi_2(u_1^{min}+2u_2^{min}x_2)\\ x_2(\tau_1)=\varepsilon_2\\ \psi_2(\tau_1)=1 \end{cases} \)
Учитывая что у нас нету особого режима нет и $$\psi_2 $$ - непрерывна
\( \dot{\psi}_2(\tau_1) = - \psi_1^0+1(u_1^{min}+2u_2^{min}x_2)<0 \)
Что означает что происходит обычное переключение $$u_3^*=0 $$ при $$t>\tau_1 $$ В итоге имеем систему дифференциальных уравнений:
\( \begin{cases} \dot{x}_2 = -(u_1^{min}+u_2^{min}x_2)x_2\\ \dot{\psi}_2 = -\psi_1^0+\psi_2(u_1^{min}+2u_2^{min}x_2)\\ x_2(\tau_1)= \varepsilon_2\\ \psi_2(\tau_1)=1 \end{cases} \)
Движение при $$\psi_2^0<1$$
Выпишем ОДУ для движение тележки, поскольку в силу (УМ) $$u_3^*(0+)=0 $$
\( \begin{cases} \dot{x}_1=x_2 \\ \dot{x}_2 = -(u_1+u_2x_2)x_2 \\ \dot{\psi}_1 = 0 \\ \dot{\psi}_2 = -\psi_1^0+\psi_2(u_1+2u_2x_2)\\ x_2(0)=0 \\ \end{cases} \)
В силу единственности, для этой системы $$x_2 \equiv 0 $$ $$-$$ единственное решение.
Следовательно, движение $$\tau_{\textbf{нач}} $$ начнется тогда, когда $$u_3>0 $$, то есть будет $$\psi_2 \geq 1 $$ учитывая непрерывность :
\( \psi_2(\tau_\textbf{нач})=1, \quad \psi_2(t) > 1 \quad t \in (\tau_\textbf{нач},\tau_\textbf{нач} +\delta) \)
В этот момент произойдёт переключение по остальным компонентам управления, и начнётся движение:
\( u_1^* = u_1^{max},u_2^* = u_1^{min} \quad t > \tau_{\textbf{нач}} \)
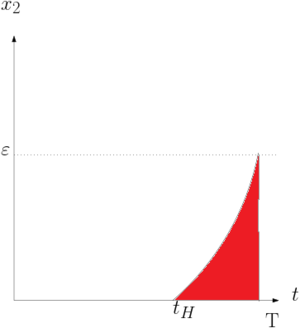
Из рассмотренного случая при $$\psi_2>1$$, имеем ровно одно переключение. То есть , если $$x_2(t) > \varepsilon$$ - то не будет достигнуто краевое условие, из единственности решения задачи Коши.
Учитывая начальное условие:
\( L > T \varepsilon \)
Площадь криволинейной трапеции меньше площади прямоугольника:
\( L = \int\limits_0^T x_2(\tau) d \tau \leq \varepsilon (T - \tau_{\textbf{нач}}) <T \varepsilon \)
Случай невозможен. Получили противоречие с краевыми условиями.
Движение при $$\psi_2^0=1$$
Данный случай полностью повторяет предыдущий пункт, однако теперь
возможен вариант $$\tau_{\textbf{нач}} = 0$$.
Так или иначе, условие $$L > T \varepsilon $$ всё ещё делает
этот случай невозможным.
Анормальный случай
\( \psi_0 =0 \)
Отличие в $$u_2^*$$:
\( u_3^*= \begin{cases} u_3^{max}, & \psi_2>0 \\ [0,u_3^{max}], & \psi_2=0 \\ 0, & \psi_2<0 \end{cases} \)
Остальные компоненты управления остаются такими же\[ u_1^*= \begin{cases} u_1^{min}, & \psi_2x_2>0 \\ [u_1^{min},u_1^{max}], & \psi_2x_2=0 \\ u_1^{max}, & \psi_2x_2<0 \end{cases} u_2^*= \begin{cases} u_2^{min}, & \psi_2>0,x_2 \neq 0 \\ [u_2^{min},u_2^{max}], & \psi_2x_2=0 \\ u_2^{max}, & \psi_2<0,x_2 \neq 0 \end{cases} \] Пусть $$ \psi_2^0 >0$$. Предположим что при переходе через $$\psi_2=0 $$ возможен особый режим
\( 0 = \dot{\psi}_2 = - \psi_1^0 + 0\cdot (...) \Rightarrow \psi_1^0=0 \Rightarrow (\psi_0,\psi_1,\psi_2)=0 \)
Это происходит на отрезке ненулевой меры , получаем противоречие (УН).
То есть особый режим невозможен, происходит простое переключение по всем трем компонентам.
Перепараметризуем, переходим к параметру $$\tau_1: \psi_2(\tau_1) = 0.$$
Поскольку при этом $$\psi(\tau_1) \neq 0$$, то $$\psi_1(\tau_1) \neq 0$$.
Нормируем начальный момент времени: $$\psi_1(\tau_1) =1 $$
Случай $$\psi_1(\tau_1) = -1 $$ исключаем, по доказанному ранее это влечёт $$\psi_2 \uparrow$$ и торможения не будет.
Зафиксировав $$\psi_0^0, \psi_1^0 $$ и перейдя к перебору по $$ \tau_1$$, получаем
однопараметрическое семейство решений.