Метрика Хаусдорфа: различия между версиями
(Исправлены опечатки, добавлена формула для расчета метрики Хаусдорфа для двух выпуклых компактов через их опорные функции, упоминание полуметрик, ссылки на биографии) |
м |
||
| Строка 1: | Строка 1: | ||
| − | '''Метрика Хаусдорфа''' есть естественная метрика, определённая на множестве всех непустых замкнутых ограниченных подмножеств пространства. Она превращает это множество в метрическое пространство. Метрику Хаусдорфа иногда также называют | + | '''Метрика Хаусдорфа''' есть естественная метрика, определённая на множестве всех непустых замкнутых ограниченных подмножеств пространства. Она превращает это множество в метрическое пространство. Метрику Хаусдорфа иногда также называют метрикой [https://ru.wikipedia.org/wiki/Помпей,_Димитрие Помпейю]-[https://ru.wikipedia.org/wiki/Хаусдорф,_Феликс Хаусдорфа]. |
== Расстояние по Хаусдорфу == | == Расстояние по Хаусдорфу == | ||
Пусть $$(X, \rho) ~- $$ метрическое пространство. Введем понятие '''расстояния по Хаусдорфу''' между двумя непустыми ограниченными множествами. Итак, пусть $$M, N \subset X ~-$$ непустые ограниченные множества. Для них положим | Пусть $$(X, \rho) ~- $$ метрическое пространство. Введем понятие '''расстояния по Хаусдорфу''' между двумя непустыми ограниченными множествами. Итак, пусть $$M, N \subset X ~-$$ непустые ограниченные множества. Для них положим | ||
| Строка 118: | Строка 118: | ||
== Список литературы == | == Список литературы == | ||
1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2014. | 1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2014. | ||
| − | |||
| − | |||
| − | |||
| − | |||
Версия 14:15, 19 декабря 2022
Метрика Хаусдорфа есть естественная метрика, определённая на множестве всех непустых замкнутых ограниченных подмножеств пространства. Она превращает это множество в метрическое пространство. Метрику Хаусдорфа иногда также называют метрикой Помпейю-Хаусдорфа.
Содержание
Расстояние по Хаусдорфу
Пусть $$(X, \rho) ~- $$ метрическое пространство. Введем понятие расстояния по Хаусдорфу между двумя непустыми ограниченными множествами. Итак, пусть $$M, N \subset X ~-$$ непустые ограниченные множества. Для них положим \begin{gather*} h(M, N) = \inf\left\{ r > 0: O(M, r) \supseteq N, O(N, r) \supseteq M \right\}, \end{gather*}
где $$O(\cdot, r) ~-$$ открытая $$r$$-окрестность множества.
Число $$h(M, N)$$ называется расстоянием по Хаусдорфу между множествами $$M$$ и $$N$$. Кроме того, приведенная выше формула определяет расстояние по Хаусдорфу и для неограниченных множеств $$M$$ и $$N$$, однако при этом $$h(M, N)$$ уже может принимать значение $$+\infty$$.
Предложение
Для любых $$a_1, a_2 \in X$$ и $$r_1, r_2 > 0$$ справедливо неравенство \begin{gather}\label{eq1} h(B(a_1, r_1), B(a_2, r_2)) \leqslant \rho(a_1, a_2) + \max\left\{r_1, r_2\right\}, \end{gather} где $$B(a, r) ~-$$ замкнутый шар метрического пространства в точке $$a$$ с радиусом $$r$$.
Доказательство
Пусть $$x_1 \in B(a_1, r_1)$$. Тогда имеет место неравенство $$\rho(x_1, a_2) \leqslant r_1 + \rho(a_1, a_2) $$, которое вытекает из следующей цепочки неравенств: \begin{gather*} \rho(x_1, a_2) \leqslant \rho(x_1, a_1) + \rho(a_1, a_2) \leqslant r_1 + \rho(a_1, a_2). \end{gather*} Таким же образом получаем, что $$\rho(x_2, a_1) \leqslant r_2 + \rho(a_1, a_2)$$ для всех $$x_2 \in B(a_2, r_2)$$. Далее из получившихся неравенств и определения расстояния по Хаусдорфу вытекает формула (\ref{eq1}).
Замечание
Если дополнительно предположить, что $$X ~-$$ линейное нормированное пространство, то \begin{gather*} h(B(a_1, r_1), B(a_2, r_2)) = \|a_2 - a_1\| + \left|r_2 - r_1 \right|. \end{gather*}
Пример 1
Данный пример показывает, что доказанное выше неравенство (\ref{eq1}) может превратиться в равенство. Рассмотрим метрическое пространство $$(X, \rho)$$, в котором $$X = \left\{ -2, -1, 1, 2\right\} ~- $$ множество состоящее из точек на прямой с естественной метрикой расстояния между точками. Тогда при $$a_1 = -1, a_2 = 1, r_1 = r_2 = 1$$ имеет место \begin{gather*} h(B(a_1, r_1), B(a_2, r_2)) = 3 = \rho(a_1, a_2) + \max(r_1, r_2). \end{gather*}
Пример 2
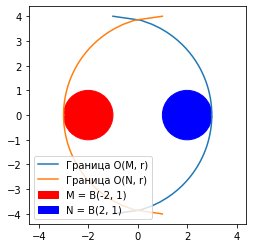
Пусть теперь возьмем на рассмотрение метрическое пространство $$(X, \rho)$$, в котором $$X = \mathbb{R}^2$$ с естественной метрикой расстояния между точками в пространстве $$\mathbb{R}^2$$. Найдем Хаусдорфово расстояние между $$B(2,1)$$ и $$B(-2,1)$$: \begin{gather*} h(B(-2, 1), B(2, 1)) = 4. \end{gather*}
Переход к метрике
Несложно видеть, что для замкнутых ограниченных множеств расстояние по Хаусдорфу $$h$$ удовлетворяет всем аксиомам метрики. А именно, для любых непустых замкнутых ограниченных множеств $$M, N$$ и $$E$$ имеют место соотношения \begin{gather*} h(M, N) = 0 \Leftrightarrow M = N, \end{gather*} \begin{gather*} h(M, N) = h(N, M) \geqslant 0, \end{gather*} \begin{gather*} h(M, N) \leqslant h(M, E) + h(E, N). \end{gather*} Таким образом, функция $$h$$ превращает множество всех непустых замкнутых ограниченных подмножеств пространства $$X$$ в метрическое пространство, которое обозначается через $$H(X)$$. Метрику $$h$$ называют метрикой Хаусдорфа. Однако в общем случае расстояние Хаусдорфа метрикой не является, так как может равняться нулю между различными множествами. Например, это имеет место для отрезка $$M = \left[a, b\right]$$ и полуинтервала $$N = \left[a, b \right)$$, которые рассматриваются как подмножества числовой прямой. Действительно, для любого $$\varepsilon > 0$$ выполняется, что $$M \subset O(N, \varepsilon)$$ и $$N \subset O(M, \varepsilon)$$, поэтому $$h(M, N) = 0$$.
Наряду с метрическим пространством обычно рассматривается его подпространство $$H_{c}(X)$$, которое состоит из непустых компактных подмножеств $$X$$. Стоит отметить, что если множество $$X$$ ограничено, то функция $$h$$ ограничена на множестве всех подмножеств множества $$X$$.
Свойства
Пусть $$(X, \rho) ~- $$ метрическое пространство, а $$M, N ~-$$ непустые подмножества пространства $$X$$.
1. Для любых $$x \in M$$ и $$\varepsilon > 0$$ существует $$y \in N$$ такое, что $$\rho(x, y) \leqslant h(M, N) + \varepsilon$$.
2. $$h(M, N) = 0$$ тогда и только тогда, когда $$\overline{M} = \overline{N}$$.
3. Пусть $$X = \mathbb{R}^n$$, а $$M, N ~-$$ выпуклые компакты. Тогда \begin{gather*} h(M, N) = \max_{\|l \| \leqslant 1}\left|s(l| M) - s(l| N) \right|, \end{gather*} где $$s(l| \cdot) ~-$$ опорная функция.
4. Если пространство $$X$$ ограничено, то метрическое пространство $$H(X)$$ сепарабельно.
5. Если пространство $$X$$ полно, то метрические пространства $$H(X)$$ и $$H_{c}(X)$$ тоже полны.
Альтернативные способы задания расстояния
Наряду с расстоянием Хаусдорфа часто используют и другое расстояние между множествами, которое обозначается через dist и определяется следующим соотношением: \begin{gather*} \text{dist}(M, N) = \inf\left\{\rho(x, y), x \in M, y \in N\right\}. \end{gather*} Для данного расстояния, очевидно, имеет место \begin{gather*} \text{dist}(M, N) \leqslant h(M, N), \end{gather*} \begin{gather*} \text{dist}(M, N) = \text{dist}(N, M) \geqslant 0. \end{gather*} Также можно рассмотреть еще одну величину, которая характеризует взаимное расположение множеств $$M$$ и $$N$$, лежащих в $$X$$. Это $$~-$$ отклонение множества $$M$$ от множества $$N$$, которое определяется соотношением \begin{gather*} h^{+}(M, N) = \inf\left\{ \varepsilon > 0: O(N, \varepsilon) \supset M\right\}. \end{gather*} Отклонение $$h^{+}$$ обычно называют полуметрикой Хаусдорфа. Наряду с $$h^+$$, можно ввести еще одну полуметрику $$h^-$$: \begin{gather*} h^{-}(M, N) = h^{+}(N, M). \end{gather*} Величину $$h^+$$ можно выразить через dist: \begin{gather*} h^{+}(M, N) = \sup\left\{ \text{dist}(x, N), x \in M\right\}, \end{gather*} а расстояние по Хаусдорфу в свою очередь выражается через $$h^+$$ и $$h^-$$ по формуле \begin{gather*} h(M, N) = \max\left\{ h^{+}(M, N), h^{-}(M, N)\right\}. \end{gather*} Поэтому для любых множест $$M, N$$ справедливо \begin{gather*} \text{dist}(M, N) \leqslant h^{+}(M, N) \leqslant h(M, N). \end{gather*}
Список литературы
1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2014.