Бифуркационная диаграмма: различия между версиями
Denis23 (обсуждение | вклад) м |
Denis23 (обсуждение | вклад) (Четвёртая версия страницы) |
||
| Строка 10: | Строка 10: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{ | + | \dot{v} = f(v, \alpha), ~ v \in \mathbb{R}, ~ \alpha \in \mathbb{R}. |
\end{gather*} | \end{gather*} | ||
| Строка 39: | Строка 39: | ||
$$ M - $$ число итераций необходимое для того, чтобы найти возможные положения равновесия в данном состоянии. | $$ M - $$ число итераций необходимое для того, чтобы найти возможные положения равновесия в данном состоянии. | ||
| − | [[Файл: | + | [[Файл:MyBifAlphaV.png|300px|мини|справа|Бифуркационная диаграмма для примера 1 при значении $$ v_0 = 0.4 $$.]] |
| − | |||
'''Шаг 1:''' | '''Шаг 1:''' | ||
Определяем отрезок $$ [ \alpha_0, \alpha_{max} ] $$ на котором будем производить исследование. | Определяем отрезок $$ [ \alpha_0, \alpha_{max} ] $$ на котором будем производить исследование. | ||
| Строка 57: | Строка 56: | ||
== Пример бифуркационной диаграммы для системы в дискретном времени== | == Пример бифуркационной диаграммы для системы в дискретном времени== | ||
'''Пример 1.''' | '''Пример 1.''' | ||
| − | [[Файл: | + | [[Файл:11AlphaV.png|300px|мини|справа|Бифуркационная диаграмма в фазово-параметрическом пространстве динамической системы примера 2.]] |
Пусть задана динамическая система: | Пусть задана динамическая система: | ||
| Строка 74: | Строка 73: | ||
'''Пример 2.''' | '''Пример 2.''' | ||
Пусть задана динамическая система: | Пусть задана динамическая система: | ||
| − | [[Файл: | + | [[Файл:12AlphaV.png|300px|мини|справа|Бифуркационная диаграмма в фазово-параметрическом пространстве |
динамической системы примера 3. Обозначения как для примера 2.]] | динамической системы примера 3. Обозначения как для примера 2.]] | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{ | + | \dot{v}= \alpha + v^2, ~ \alpha \in \mathbb{R}. |
\end{gather*} | \end{gather*} | ||
| − | В данном случае $$ | + | В данном случае $$ \alpha $$ это параметр, по которому происходит бифуркация. Такой параметр называют бифуркационным. |
Жирная линия обозначает многообразие положений равновесия, причем сплошная линия отвечает устойчивому положению равновесия, а | Жирная линия обозначает многообразие положений равновесия, причем сплошная линия отвечает устойчивому положению равновесия, а | ||
пунктирная $$ - $$ неустойчивому. Жирные точки обозначают положения равновесия. Приведены | пунктирная $$ - $$ неустойчивому. Жирные точки обозначают положения равновесия. Приведены | ||
| − | три фазовых портрета, как сечения бифуркационной диаграммы, для значений параметра $$ | + | три фазовых портрета, как сечения бифуркационной диаграммы, для значений параметра $$ \alpha_1, \alpha_c, \alpha_2. $$ |
'''Пример 3. (бифуркация типа вилки)''' | '''Пример 3. (бифуркация типа вилки)''' | ||
| Строка 91: | Строка 90: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{ | + | \dot{v}= \alpha v - v^3, ~ \alpha \in \mathbb{R}. |
\end{gather*} | \end{gather*} | ||
| − | В данном случае $$ | + | В данном случае $$ \alpha $$ это бифуркационный параметр. |
| − | Если $$ | + | Если $$ \alpha < 0, $$ то имеется единственное устойчивое положение равновесия $$ v = 0. $$ |
| − | Если же $$ | + | Если же $$ \alpha > 0, $$ то возникают два устойчивых положения равновесия $$ v_{1,2} = \pm \sqrt{\alpha}, $$ |
| − | при этом положение равновесия $$ | + | при этом положение равновесия $$ v = 0 $$ становится неустойчивым. |
Такая бифуркация называется бифуркацией типа вилки. | Такая бифуркация называется бифуркацией типа вилки. | ||
| Строка 104: | Строка 103: | ||
'''Пример 4. (бифуркация удвоения периода)''' | '''Пример 4. (бифуркация удвоения периода)''' | ||
| − | [[Файл: | + | [[Файл:BifDoubleAlphaV.png|600px|мини|справа|Появление устойчивого цикла длины два для системы из примера 4]] |
Пусть задана динамическая система: | Пусть задана динамическая система: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{ | + | \dot{v}= -(1 + \alpha)v + v^3, ~ \alpha \in \mathbb{R}. |
\end{gather*} | \end{gather*} | ||
| − | Отображение $$ | + | Отображение $$ v \mapsto -(1 + \alpha)v + v^3 $$ обратимо для малых значений $$ |\alpha| $$ в окрестности начала координат. |
| − | Динамическая система имеет [https://sawiki.cs.msu.ru//index.php/Неподвижные_точки_системы неподвижную точку] $$ | + | Динамическая система имеет [https://sawiki.cs.msu.ru//index.php/Неподвижные_точки_системы неподвижную точку] $$ v^* = 0 $$ для всех значений $$ \alpha $$ с собственным |
| − | числом $$ \mu = -(1+ | + | числом $$ \mu = -(1+\alpha). $$ Эта точка устойчива при малых $$ \alpha < 0 $$ и неустойчива, если $$ \alpha > 0. $$ |
| − | Если $$ | + | Если $$ \alpha = 0, $$ то $$ \mu = -1, $$ поэтому в этом случае линейный анализ недостаточен для изучения устойчивости. |
| − | Вторая итерация отображения $$ | + | Вторая итерация отображения $$ v \mapsto -(1 + \alpha)v + v^3 = f^2(v, \alpha) $$ имеет вид: |
\begin{gather*} | \begin{gather*} | ||
| − | f^2( | + | f^2(v, \alpha) = f(f(v, \alpha)) = -(1+\alpha)[-(1+\alpha)v + v^3] + [-(1+\alpha)v + v^3]^3 = \\ |
| − | = (1+ | + | = (1+\alpha)^2 v - (1+\alpha) v^3 - (1+\alpha)^3 v^3 + o(v^3) = \\ |
| − | = (1+ | + | = (1+\alpha)^2 v - (2 + 4\alpha + 3\alpha^2 + \alpha^3) v^3 + o(v^3). |
\end{gather*} | \end{gather*} | ||
| − | Отображение $$ f^2( | + | Отображение $$ f^2(v, \alpha), $$ очевидно, имеет тривиальную неподвижную точку $$ v^* = 0. $$ Кроме того, оно имеет |
| − | ещё две неподвижные точки при малых значениях параметра $$ | + | ещё две неподвижные точки при малых значениях параметра $$ \alpha > 0: v^*_{1,2} = \sqrt{\alpha} + o(\sqrt{\alpha}). $$ Последнее |
| − | означает, что $$ | + | означает, что $$ v^*_2 = f(v^*_1, \alpha), \, v^*_1 = f(v^*_2, \alpha), $$ причём $$ v^*_1 \neq v^*_2. $$ |
| − | Нетрудно показать, что во второй итерации отображения $$ f( | + | Нетрудно показать, что во второй итерации отображения $$ f(v, \alpha) $$ происходит бифуркация типа вилки. |
| − | Две неподвижные точки, появляющиеся в $$ f^2( | + | Две неподвижные точки, появляющиеся в $$ f^2(v, \alpha) $$ при $$ \alpha > 0, $$ устойчивы и образуют |
[https://sawiki.cs.msu.ru//index.php/Циклы_в_системах_с_дискретным_временем._Теорема_Шарковского цикл] длины | [https://sawiki.cs.msu.ru//index.php/Циклы_в_системах_с_дискретным_временем._Теорема_Шарковского цикл] длины | ||
| − | два для исходного отображения $$ f( | + | два для исходного отображения $$ f(v, \alpha), $$ так как $$ f(v^*_1, \alpha) = v^*_2 $$ и $$ f(v^*_2, \alpha) = v^*_1. $$ |
Такая бифуркация в исходной системе называется бифуркацией удвоения периода. | Такая бифуркация в исходной системе называется бифуркацией удвоения периода. | ||
| − | Если параметр $$ | + | Если параметр $$ \alpha $$ изменяется в направлении от положительных значений к отрицательным, то |
| − | амплитуда цикла уменьшается (в том смысле, что $$ | + | амплитуда цикла уменьшается (в том смысле, что $$ v^*_1 $$ и $$ v^*_2 $$ стремятся друг к другу), |
затем цикл исчезает. На рисунке к данному примеру показано появление устойчивого цикла длины 2 | затем цикл исчезает. На рисунке к данному примеру показано появление устойчивого цикла длины 2 | ||
в системе. | в системе. | ||
== Самоподобие бифуркационных диаграмм== | == Самоподобие бифуркационных диаграмм== | ||
| − | [[Файл: | + | [[Файл:BifSamo11.png|300px|мини|справа|Бифуркационная диаграмма для примера 5 самоподобия бифуркационных диаграмм на интервале $$ \alpha \in [2, 2.02] $$.]] |
| + | |||
| + | '''Пример 5.''' | ||
Приведём пример самоподобия бифуркационных диаграмм для системы: | Приведём пример самоподобия бифуркационных диаграмм для системы: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{ | + | \dot{v}= v^2 e^{\alpha (1-v^2)}, ~ \alpha \in \mathbb{R}. |
\end{gather*} | \end{gather*} | ||
| − | На диаграммах, приведённых справа, можно наблюдать самоподобие при $$ | + | На диаграммах, приведённых справа, можно наблюдать самоподобие при $$ \alpha \in [2, 2.02] |
| − | $$ и $$ | + | $$ и $$ \alpha \in [2.0075, 2.012]. $$ Внешний вид ветвления остаётся очень похожим. |
| − | + | [[Файл:BifSamo12.png|300px|мини|справа|Бифуркационная диаграмма для примера 5 самоподобия бифуркационных диаграмм на интервале $$ \alpha \in [2.0075, 2.012] $$.]] | |
| − | [[Файл: | ||
| − | |||
== Список литературы == | == Список литературы == | ||
# Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | ||
# Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011 | # Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011 | ||
Версия 17:56, 10 октября 2023
Содержание
Определение
Определение Бифуркационной диаграммой динамической системы называется разбиение пространства параметров на максимальные связные подмножества, которые определяются соотношениями топологической эквивалентности и рассматриваются вместе с фазовыми портретами для каждого элемента разбиения.
Смысл
\begin{gather*} \dot{v} = f(v, \alpha), ~ v \in \mathbb{R}, ~ \alpha \in \mathbb{R}. \end{gather*}
Пояснение: Несмотря на то, что приведённая динамическая система является системой в непрерывном времени, бифуркационная диаграмма строится и для дискретных динамических систем, определение и алгоритм построения остаются теми же.
Зафиксируем некоторое значение вектора параметров $$ \alpha = \alpha_0 $$ и рассмотрим в пространстве параметров максимальное связное множество, содержащее $$ \alpha_0, $$ такое, что во всех его точках вышеприведённая система топологически эквивалентна этой же системе при $$ \alpha = \alpha_0. $$ Рассматривая такие множества в пространстве параметров, получим так называемый параметрический портрет вышеприведённой системы. Параметрический портрет вместе с характерными для каждого множества параметров фазовыми портретами составляют бифуркационную диаграмму.
При качественном анализе динамической системы желательно получить ее бифуркационную диаграмму, так как в ней в сжатом виде содержатся все возможные модели поведения данной системы.
Алгоритм построения бифуркационной диаграммы
Пусть задана динамическая система в дискретном времени: \begin{gather*} v_{t+1} = g(v_t, \alpha), ~ v \in \mathbb{R}, ~ \alpha \in \mathbb{R}. \end{gather*}
Введём необходимые обозначения:
$$ N - $$ число итераций необходимое для того, чтобы траектория системы сошлась к некоторому постоянному состоянию,
$$ M - $$ число итераций необходимое для того, чтобы найти возможные положения равновесия в данном состоянии.
Шаг 1: Определяем отрезок $$ [ \alpha_0, \alpha_{max} ] $$ на котором будем производить исследование.
Шаг 2: Запускаем цикл по $$ j $$ от $$ 1 $$ до $$ N, $$ перебирая по равномерной сетке все значения $$ \alpha. $$
Шаг 3: Для каждого значения $$ \alpha_j $$ запускаем цикл по $$ i $$ от $$ 1 $$ до $$ N, $$ в котором находим $$ v_i = g(v_{i-1}). $$ Таким образом, получаем $$ v_N. $$
Шаг 4: Для каждого такого $$ \alpha_j, $$ при уже найденном $$ v_N, $$ запускаем новый цикл по $$ i $$ от $$ 1 $$ до $$ M, $$ в котором производим ещё $$ M $$ итераций нахождения $$ v_i = g(v_{i-1}). $$ Каждое полученное значение $$ v_i $$ заносим на график как точку с координатами $$ ( \alpha_j, v_i) . $$
Бифуркационная диаграмма получена.
Пример бифуркационной диаграммы для системы в дискретном времени
Пример 1.
Пусть задана динамическая система:
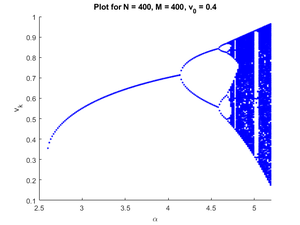
\begin{gather*} {v}_{t+1}= \alpha {v_t}^{\frac{3}{2}} (1 - v_t), ~ \alpha \in \mathbb{R}. \end{gather*} Тогда бифуркационные диаграммы приведены в правой части страницы.
$$ N $$ и $$ M $$ соответствуют своему описанию из секции Алгоритм построения бифуркационной диаграммы.
$$ v_0 $$ $$ - $$ точка, в которой происходит поиск.
Примеры бифуркационных диаграмм для систем в непрерывном времени
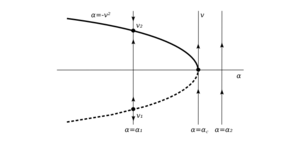
Пример 2. Пусть задана динамическая система:
\begin{gather*} \dot{v}= \alpha + v^2, ~ \alpha \in \mathbb{R}. \end{gather*}
В данном случае $$ \alpha $$ это параметр, по которому происходит бифуркация. Такой параметр называют бифуркационным.
Жирная линия обозначает многообразие положений равновесия, причем сплошная линия отвечает устойчивому положению равновесия, а пунктирная $$ - $$ неустойчивому. Жирные точки обозначают положения равновесия. Приведены три фазовых портрета, как сечения бифуркационной диаграммы, для значений параметра $$ \alpha_1, \alpha_c, \alpha_2. $$
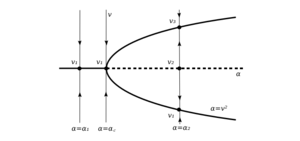
Пример 3. (бифуркация типа вилки) Пусть задана динамическая система:
\begin{gather*} \dot{v}= \alpha v - v^3, ~ \alpha \in \mathbb{R}. \end{gather*}
В данном случае $$ \alpha $$ это бифуркационный параметр.
Если $$ \alpha < 0, $$ то имеется единственное устойчивое положение равновесия $$ v = 0. $$ Если же $$ \alpha > 0, $$ то возникают два устойчивых положения равновесия $$ v_{1,2} = \pm \sqrt{\alpha}, $$ при этом положение равновесия $$ v = 0 $$ становится неустойчивым.
Такая бифуркация называется бифуркацией типа вилки.
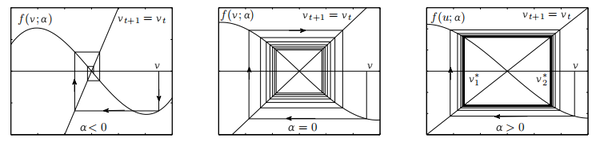
Пример 4. (бифуркация удвоения периода)
Пусть задана динамическая система:
\begin{gather*} \dot{v}= -(1 + \alpha)v + v^3, ~ \alpha \in \mathbb{R}. \end{gather*}
Отображение $$ v \mapsto -(1 + \alpha)v + v^3 $$ обратимо для малых значений $$ |\alpha| $$ в окрестности начала координат. Динамическая система имеет неподвижную точку $$ v^* = 0 $$ для всех значений $$ \alpha $$ с собственным числом $$ \mu = -(1+\alpha). $$ Эта точка устойчива при малых $$ \alpha < 0 $$ и неустойчива, если $$ \alpha > 0. $$ Если $$ \alpha = 0, $$ то $$ \mu = -1, $$ поэтому в этом случае линейный анализ недостаточен для изучения устойчивости.
Вторая итерация отображения $$ v \mapsto -(1 + \alpha)v + v^3 = f^2(v, \alpha) $$ имеет вид: \begin{gather*} f^2(v, \alpha) = f(f(v, \alpha)) = -(1+\alpha)[-(1+\alpha)v + v^3] + [-(1+\alpha)v + v^3]^3 = \\ = (1+\alpha)^2 v - (1+\alpha) v^3 - (1+\alpha)^3 v^3 + o(v^3) = \\ = (1+\alpha)^2 v - (2 + 4\alpha + 3\alpha^2 + \alpha^3) v^3 + o(v^3). \end{gather*}
Отображение $$ f^2(v, \alpha), $$ очевидно, имеет тривиальную неподвижную точку $$ v^* = 0. $$ Кроме того, оно имеет ещё две неподвижные точки при малых значениях параметра $$ \alpha > 0: v^*_{1,2} = \sqrt{\alpha} + o(\sqrt{\alpha}). $$ Последнее означает, что $$ v^*_2 = f(v^*_1, \alpha), \, v^*_1 = f(v^*_2, \alpha), $$ причём $$ v^*_1 \neq v^*_2. $$ Нетрудно показать, что во второй итерации отображения $$ f(v, \alpha) $$ происходит бифуркация типа вилки.
Две неподвижные точки, появляющиеся в $$ f^2(v, \alpha) $$ при $$ \alpha > 0, $$ устойчивы и образуют цикл длины два для исходного отображения $$ f(v, \alpha), $$ так как $$ f(v^*_1, \alpha) = v^*_2 $$ и $$ f(v^*_2, \alpha) = v^*_1. $$ Такая бифуркация в исходной системе называется бифуркацией удвоения периода.
Если параметр $$ \alpha $$ изменяется в направлении от положительных значений к отрицательным, то амплитуда цикла уменьшается (в том смысле, что $$ v^*_1 $$ и $$ v^*_2 $$ стремятся друг к другу), затем цикл исчезает. На рисунке к данному примеру показано появление устойчивого цикла длины 2 в системе.
Самоподобие бифуркационных диаграмм
Пример 5.
Приведём пример самоподобия бифуркационных диаграмм для системы: \begin{gather*} \dot{v}= v^2 e^{\alpha (1-v^2)}, ~ \alpha \in \mathbb{R}. \end{gather*} На диаграммах, приведённых справа, можно наблюдать самоподобие при $$ \alpha \in [2, 2.02] $$ и $$ \alpha \in [2.0075, 2.012]. $$ Внешний вид ветвления остаётся очень похожим.
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011