Логистическое уравнение и его свойства

Логистическое уравнение - уравнение, описывающее численность изолированной популяции в момент времени $$t$$ и имеющее вид

\[ \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right) , \]

где $$r, K$$ - положительные параметры модели.

История возникновения

Пусть $$ N(t) $$ — численность изолированной популяции в момент времени $$ t $$. Скорость её изменения может быть представлена в следующем виде

\[ \dot N = \text{рождаемость} - \text{смертность} + \text{миграция} . \]

Вид различных членов в правой части этого уравнения зависит от конкретных условий существования популяций и присущих ей свойств. В простейшем случае предполагается отсутствие миграции, а члены рождаемости и смертности пропорциональны общей численности популяции $$ N $$:

\[ \dot N = bN - cN, \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \dot N = aN, \ a = b - c .\]

Поскольку в действительности наблюдаются стабильные популяции, то необходимо рассматривать математические модели, в которых плотность популяции играет регулирующую роль. Очевидно, что коэффициент размножения в такой модели должен быть не постоянным, а зависящим от численности или плотности. Более точно, математическая модель роста замкнутой популяции имеет вид

\[ \dot N = N \cdot f(N) , \]

где $$ f(N) $$ — коэффициент скорости роста популяции. Разложим $$ F(N) $$ в ряд Тейлора в окрестности нуля и отбросим все члены, кроме первых двух. Получим

\[ \dot N = N(a + bN), \]

где $$ a,b $$ — некоторые постоянные, причем естественно предположить, что $$ a > 0, \ b < 0 $$. Именно таким образом Альфред Лотка пришел к уравнению, которое стало известно как логистическое уравнение, которое после некоторых переобозначений запишется в виде:

\[ \dot N = rN \left( 1 - \dfrac{N}{K} \right) . \]

Здесь $$ r $$ и $$K$$ — положительные параметры.

Свойства

Можно заметить, что когда $$ N(t) $$ мало, то $$ \dot N \approx rN $$. Значит, $$N$$ экспоненциально растёт. Параметр $$ K $$ интерпретируется как потенциальная емкость экологической системы, которая определяется доступным наличным количеством ресурсов. Величина $$ K $$ определяет предельное значение численности популяции. Для доказательства этого факта решим логистическое уравнение:

\[ \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right), \]

\[ -\dfrac{1}{r} \int \dfrac{dN}{\frac{N^2}{K} - N} = \int dt , \]

\[ -\dfrac{1}{r} \int \dfrac{dN}{ \left( \frac{N}{\sqrt{K}} - \frac{1}{2} \sqrt{k} \right)^2 - \frac{1}{4}k} = \int dt . \]

Сделаем замену в правой части равенства: $$ z = \frac{N}{\sqrt{K}} - \frac{1}{2} \sqrt{k}, \ dz = \frac{dN}{\sqrt{k}} $$. Получим

\[ - \dfrac{\sqrt{K}}{r} \int \dfrac{dz}{z^2 - \frac{1}{4} k} = \int dt , \]

\[ -\dfrac{1}{r} \ln{ \left| \dfrac{z - \frac{1}{2} \sqrt{k} }{z + \frac{1}{2} \sqrt{k}} \right| } = t + C , \]

\[ \dfrac{z - \frac{1}{2} \sqrt{k} }{z + \frac{1}{2} \sqrt{k}} = Ce^{-rt} . \]

Возвращаясь к N, получим

\[ 1 - \dfrac{K}{N} = C e^{-rt} ,\] \[ N = \dfrac{K}{1 - Ce^{-rt}}. \]

Найдем $$ C $$ из начального условия $$ N(0) = N_0: \ C = 1 - \frac{K}{N_0}. $$ Окончательно получим

\[ N(t) = \dfrac{K}{1 - \left( 1 - \frac{K}{N_0} \right) e^{-rt} } = \dfrac{K e^{rt} }{e^{rt} - 1 + \frac{K}{N_0}} = \dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . \]

Это решение для $$ 0 < N_0 < K $$ представляет собой сигмоидальную кривую, которая также часто называют логистической кривой

Таким образом, $$ N(t) \rightarrow K$$ при $$ t \rightarrow +\infty $$. Тем самым, величина $$ K$$ определяет финальное состояние численности популяции.

Очевидно, что логистическое уравнение не следует воспринимать буквально как уравнение, управляющее популяционной динамикой реальных систем (например, критику логистического закона роста можно найти в статье автора классического учебника по теории вероятностей В. Феллера [3]). Наиболее правильным представляется использование логистического уравнения как самой простой и удобной формы описания популяции, численность которой стремится к некоторой конечной фиксированной величине. Логистическое уравнение — это первое приближение к описанию численности популяции с плотностно-зависимым регуляторным механизмом, на динамику которой влияют эффекты перенаселения и ограниченности ресурсов. Существенным недостатком модели является тот факт, что предельная численность популяции вводится в качестве известного параметра, в то время как отыскание этой величины нередко является основной задачей исследования.

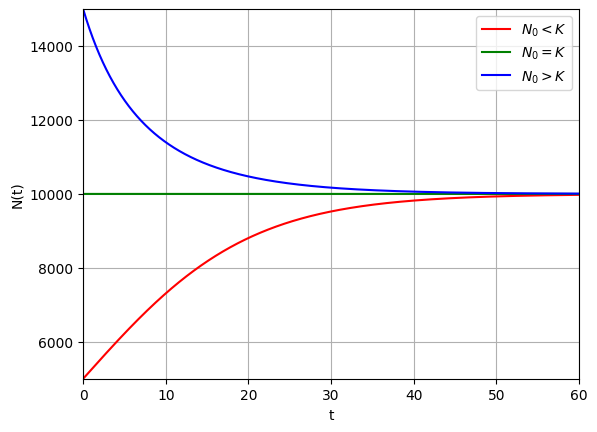
Проиллюстрируем поведение $$N(t)$$ при $$ N(0) < K, \ N(0) = K, \ N(0) > K $$.

Мы получили, что функция $$N(t)$$ монотонно сходится к параметру $$K$$ при стремлении времени к бесконечности.

Дискретная система с дискретным временем

Рассмотрим теперь дискретный вариант логистического уравнения, которое имеет вид

\[ N_{t+1} = r N_t \left( 1 - \dfrac{N_t}{K} \right) , \ \ \ r, K > 0 . \]

Это уравнение можно получить, используя явную схему дискретизации для логистического уравнения, т.е. заменяя производную по времени на разность $$ \dot N = \frac{\Delta N}{\Delta t} $$, где $$ \Delta N = N(t + \Delta t) - N (t)$$ . Если мы положим $$ \Delta t = 1 $$, то из непрерывного варианта получим

\[ N(t+1) = N(t) + r N(t) \left( 1 - \dfrac{N_t}{K} \right) , \]

от которого с помощью очевидных переобозначений можно перейти к дискретным логистическим уравнением.

Список литературы

1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.

2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.

3. Feller W. On the Logistic Law of Growth and Its Empirical Verification in Biology, Acta Biotheoretica, 5, 1940, 51–65.