Система Лотки-Вольтерры с учётом внутривидовой конкуренции: различия между версиями
(Новая страница: «== Биологическая интерпретация характеристик системы == Модель [https://sawiki.cs.msu.ru/index.php/Систе...») |
|||
| Строка 1: | Строка 1: | ||
== Биологическая интерпретация характеристик системы == | == Биологическая интерпретация характеристик системы == | ||
| − | Модель [https://sawiki.cs.msu.ru/index.php/Система_Лотки-Вольтерры._Принцип_Вольтерры Лотки | + | Модель [https://sawiki.cs.msu.ru/index.php/Система_Лотки-Вольтерры._Принцип_Вольтерры Лотки-Вольтерры] описывает взаимодействие двух видов, один из которых является хищником, а другой — жертвой. Если $$u(t)$$ — численность жертв, $$v(t)$$ — численность хищников в момент времени $$t$$, то модель имеет вид |
\begin{equation}\label{sys1} | \begin{equation}\label{sys1} | ||
\begin{cases} | \begin{cases} | ||
| Строка 7: | Строка 7: | ||
\end{cases} | \end{cases} | ||
\end{equation} | \end{equation} | ||
| − | где $a, b, c, d > 0.$ | + | где $$a, b, c, d > 0.$$ |
| − | + | ||
| − | Рассматривая систему \ref{sys1} в качестве математической модели взаимодействующих популяций, естественно считать фазовым пространством множество $\mathbb{R}^2_+ = {u, v: ~ u \geq 0, v\geq 0}$, которое является инвариантным. | + | Рассматривая систему \ref{sys1} в качестве математической модели взаимодействующих популяций, естественно считать фазовым пространством множество $$\mathbb{R}^2_+ = \{u, v: ~ u \geq 0, v\geq 0\}$$, которое является инвариантным. |
| − | + | ||
| − | Заметим, что если отсутствуют хищники, то в математической модели \ref{sys1} популяция жертв экспоненциально растёт. Естественно изменить модель таким образом, чтобы ограничить рост жертв. Кроме того, хотя это и менее критично в рассматриваемой модели, введём | + | Заметим, что если отсутствуют хищники, то в математической модели \ref{sys1} популяция жертв экспоненциально растёт. Естественно изменить модель таким образом, чтобы ограничить рост жертв. Кроме того, хотя это и менее критично в рассматриваемой модели, введём слагаемое, ограничивающее рост популяции хищников. Получим: |
\begin{equation}\label{sys2} | \begin{equation}\label{sys2} | ||
| − | \begin{ | + | \begin{cases} |
\dot{u} = au - buv - eu^2, \\ | \dot{u} = au - buv - eu^2, \\ | ||
\dot{v} = - cv + duv - fv^2, | \dot{v} = - cv + duv - fv^2, | ||
| − | \end{ | + | \end{cases} |
\end{equation} | \end{equation} | ||
| − | где $a, b, c, d, e, f > 0, (u, v) \in \mathbb{R}^2_+$. | + | где $$a, b, c, d, e, f > 0, (u, v) \in \mathbb{R}^2_+$$. |
| − | + | ||
Заметим, что \ref{sys2} отличается от \ref{sys1} последним слагаемым. Из вида этого слагаемого можно сделать вывод: чем меньше в популяции особей, тем меньше они конкурируют между собой. | Заметим, что \ref{sys2} отличается от \ref{sys1} последним слагаемым. Из вида этого слагаемого можно сделать вывод: чем меньше в популяции особей, тем меньше они конкурируют между собой. | ||
== Введение безразмерных переменных == | == Введение безразмерных переменных == | ||
| − | Введём замену переменных $t = T\tau, \, x = Ap\left(\tau\right), \, y = Bq\left(\tau\right)$. Здесь $T, A, B$ | + | Введём замену переменных $$t = T\tau, \, x = Ap\left(\tau\right), \, y = Bq\left(\tau\right)$$. Здесь $$T, A, B$$ — положительные постоянные. Далее можем записать: |
| − | + | <math>\frac{d}{dt} = \frac{d}{d\tau} \cdot\frac{d\tau}{dt} = \frac{1}{T}\cdot\frac{d}{d\tau}.</math> | |
Тогда систему \ref{sys2} можно записать в виде: | Тогда систему \ref{sys2} можно записать в виде: | ||
| − | + | <math>\begin{cases} | |
\frac{A}{T}\dot{p} = aAp - bApBq - eA^2p^2, \\ | \frac{A}{T}\dot{p} = aAp - bApBq - eA^2p^2, \\ | ||
\frac{B}{T}\dot{q} = -cBq + dApBq - fB^2q^2. | \frac{B}{T}\dot{q} = -cBq + dApBq - fB^2q^2. | ||
| − | \end{ | + | \end{cases}</math> |
Упростим оба уравнения системы: | Упростим оба уравнения системы: | ||
| − | + | \begin{cases} | |
\dot{p} = aTp - bTBpq - eTAp^2, \\ | \dot{p} = aTp - bTBpq - eTAp^2, \\ | ||
| − | \dot{q} = - cTq + dTApq - fTBq^2 | + | \dot{q} = - cTq + dTApq - fTBq^2. |
| − | \end{ | + | \end{cases}<math/> |
Пусть теперь | Пусть теперь | ||
| − | + | \begin{equation*} | |
| + | T = \frac{1}{a}, \quad B = \frac{a}{b},\quad A = \frac{a}{d}. | ||
| + | \end{equation*} | ||
Тогда система будет выглядеть следующим образом: | Тогда система будет выглядеть следующим образом: | ||
| − | + | \begin{cases} | |
\dot{p} = p - pq - \frac{e}{d}p^2, \\ | \dot{p} = p - pq - \frac{e}{d}p^2, \\ | ||
\dot{q} = - \frac{c}{a}q + pq - \frac{f}{b}q^2. | \dot{q} = - \frac{c}{a}q + pq - \frac{f}{b}q^2. | ||
| − | \end{ | + | \end{cases}<math/> |
Обозначим | Обозначим | ||
| − | + | \begin{equation*} | |
| + | \alpha = \frac{e}{d}, \quad \gamma = \frac{c}{a}, \quad \beta = \frac{f}{b}, \quad u = p, \quad v = q. | ||
| + | \end{equation*} | ||
Тогда финальная система имеет вид: | Тогда финальная система имеет вид: | ||
\begin{equation}\label{sys3} | \begin{equation}\label{sys3} | ||
| − | \begin{ | + | \begin{cases} |
\dot{u} = u - uv - \alpha u^2, \\ | \dot{u} = u - uv - \alpha u^2, \\ | ||
\dot{v} = -\gamma v + uv - \beta v^2, | \dot{v} = -\gamma v + uv - \beta v^2, | ||
| − | \end{ | + | \end{cases} |
\quad (u, v)\in \mathbb{R}^2_+, \quad \alpha > 0,\quad \beta > 0,\quad \gamma > 0. | \quad (u, v)\in \mathbb{R}^2_+, \quad \alpha > 0,\quad \beta > 0,\quad \gamma > 0. | ||
\end{equation} | \end{equation} | ||
| + | |||
| + | == Исследование неподвижных точек и характера их устойчивости == | ||
| + | Для нахождения [https://sawiki.cs.msu.ru/index.php/Неподвижные_точки_системы особых точек] системы \ref{sys3} необходимо решить следующую систему: | ||
| + | \begin{equation}\label{ot} | ||
| + | \begin{cases} | ||
| + | u(1 - v - \alpha u) = 0, \\ | ||
| + | v(-\gamma + u - \beta v) = 0. | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
| + | Очевидно, точка $$O(0, 0)$$ является решением. | ||
| + | |||
| + | Точка $$A(0, -\frac{\gamma}{\beta})$$ является решением системы \ref{ot}, но не лежит в $$\mathbb{R}^2_+$$, следовательно, не является точкой покоя. | ||
| + | |||
| + | Точка $$B(\frac{1}{\alpha}, 0)$$ является точкой покоя. | ||
| + | |||
| + | Последнюю точку покоя получаем как решение системы: | ||
| + | \begin{equation*} | ||
| + | \begin{cases} | ||
| + | 1 - v - \alpha u = 0, \\ | ||
| + | -\gamma + u - \beta v = 0. | ||
| + | \end{cases} | ||
| + | \end{equation*} | ||
| + | Обозначим | ||
| + | \begin{equation}\label{resh} | ||
| + | u^\ast = \dfrac{\gamma + \beta}{1 + \alpha \beta}, \quad v^\ast = \dfrac{1 - \alpha\gamma}{1 + \alpha\beta}. | ||
| + | \end{equation} | ||
| + | Итак, ещё одна особая точка — $$M(u^\ast, v^\ast)$$. | ||
| + | |||
| + | Найдём [https://sawiki.cs.msu.ru/index.php/Матрица_Якоби._Лемма_о_выпрямлении_векторного_поля матрицу Якоби] для системы \ref{sys3}: | ||
| + | \begin{equation}\label{j1} | ||
| + | J \left(x, y\right)= | ||
| + | \begin{pmatrix} | ||
| + | \dfrac{\partial f_1}{\partial u} & \dfrac{\partial f_1}{\partial v} \\ | ||
| + | \\ | ||
| + | \dfrac{\partial f_2}{\partial u} & \dfrac{\partial f_2}{\partial v} | ||
| + | \end{pmatrix} | ||
| + | = | ||
| + | \begin{pmatrix} | ||
| + | 1 - v - 2\alpha u & -u \\ | ||
| + | \\ | ||
| + | v & -\gamma + u -2\beta v | ||
| + | \end{pmatrix} | ||
| + | \end{equation} | ||
| + | |||
| + | $$\quad\quad$$ 1. Посчитаем значения матрицы Якоби в точке $$O$$: | ||
| + | \begin{equation*} | ||
| + | J \left(0,0\right)= | ||
| + | \begin{pmatrix} | ||
| + | 1 & 0 \\ | ||
| + | 0 & -\gamma | ||
| + | \end{pmatrix}. | ||
| + | \end{equation*} | ||
| + | В данном случае собственные значения матрицы вычисляются легко: | ||
| + | $$\lambda_1 = 1, ~ \lambda_2 = -\gamma.$$ | ||
| + | Получили, что $$\lambda_{1, 2} \in \mathbb{R}, ~\lambda_1 \cdot \lambda_2 < 0$$, значит $$O$$ — [https://sawiki.cs.msu.ru/index.php/Классификация_особых_точек_в_двумерном_пространстве седло] по определению. Напомним, что седло — всегда неустойчивое положение равновесия. | ||
| + | |||
| + | $$\quad\quad$$ 2. Посчитаем значения матрицы Якоби в точке $$B$$: | ||
| + | \begin{equation*} | ||
| + | J \bigg(\dfrac{1}{\alpha},0\bigg)= | ||
| + | \begin{pmatrix} | ||
| + | -1 & -\dfrac{1}{\alpha} \\ | ||
| + | 0 & -\gamma + \dfrac{1}{\alpha} | ||
| + | \end{pmatrix}. | ||
| + | \end{equation*} | ||
| + | Рассмотрим характеристический многочлен полученной матрицы: | ||
| + | \begin{equation*} | ||
| + | \chi = \bigg(\lambda + 1\bigg)\bigg(\lambda - \bigg(\dfrac{1}{\alpha} - \gamma\bigg)\bigg) | ||
| + | \end{equation*} | ||
| + | Теперь можем найти собственные значения: | ||
| + | \begin{equation*} | ||
| + | \lambda_1 = -1, \quad \lambda_2 = \dfrac{1}{\alpha} - \gamma, \quad \lambda_{1, 2} \in \mathbb{R}. | ||
| + | \end{equation*} | ||
| + | Если $$\alpha \gamma < 1$$, то $$\lambda_1 \cdot \lambda_2 < 0$$, и $$B$$ — [https://sawiki.cs.msu.ru/index.php/Классификация_особых_точек_в_двумерном_пространстве седло] по определению. | ||
| + | |||
| + | Если $$\alpha \gamma > 1$, то $\lambda_2 < 0,~ \lambda_1 \cdot \lambda_2 > 0$$, и $$B$$ — [https://sawiki.cs.msu.ru/index.php/Классификация_особых_точек_в_двумерном_пространстве устойчивый узел] по определению. | ||
| + | |||
| + | $$\quad\quad$$ 3. Посчитаем значения матрицы Якоби в точке $$M$$: | ||
| + | \begin{equation*} | ||
| + | J \bigg(u^\ast, v^\ast\bigg)= | ||
| + | \begin{pmatrix} | ||
| + | -\alpha u^\ast & -u^\ast \\ | ||
| + | v^\ast & -\beta v^\ast | ||
| + | \end{pmatrix}. | ||
| + | \end{equation*} | ||
| + | Вспомним ''условие устойчивости'' особой точки для общей схемы исследования: | ||
| + | \begin{equation} | ||
| + | \Tr J < 0, \quad \det J > 0. | ||
| + | \end{equation} | ||
| + | Заметим, что при $$\alpha \gamma > 1$$ точку $$M$$ рассматривать не нужно, так как из \ref{resh}: $$~v^\ast < 0$$ и $$M \notin \mathbb{R}^2_+$$. | ||
| + | |||
| + | Тогда в нашей задаче | ||
| + | \begin{equation*} | ||
| + | \Tr J(u^\ast, v^\ast) = -\alpha u^\ast - \beta v^\ast < 0, \quad \det J(u^\ast, v^\ast) = u^\ast v^\ast (1 + \alpha \beta) > 0. | ||
| + | \end{equation*} | ||
| + | Таким, образом, $$M$$ — устойчивое положение равновесия. | ||
| + | |||
| + | Объединим все полученные выше случаи. Если $$\alpha \gamma < 1$$, то особые точки $$O, ~ B$$ неустойчивые, а $$M$$ устойчивая. Если $$\alpha \gamma > 1$$, то $$O$$ — неустойчивая особая точка, $$B$$ — устойчивый узел. | ||
| + | |||
| + | == Построение фазовых портретов системы == | ||
| + | В отличие от классической модели [https://sawiki.cs.msu.ru/index.php/Система_Лотки-Вольтерры._Принцип_Вольтерры Лотки-Вольтерры], переменные в уравнении для траекторий не разделяются, поэтому для анализа [https://sawiki.cs.msu.ru/index.php/Фазовые_и_интегральные_кривые._Фазовое_пространство фазового портрета] применим метод нуль-изоклин. Разделим $$\mathbb{R}^2_+$$ на области прямыми | ||
| + | \begin{equation*} | ||
| + | v^\ast = 1 - \alpha u^\ast,\quad ~ u^\ast = \gamma + \beta v^\ast. | ||
| + | \end{equation*} | ||
| + | Тогда в полученных областях сможем оценить направление траекторий, тем самым построив "набросок" фазового портрета. | ||
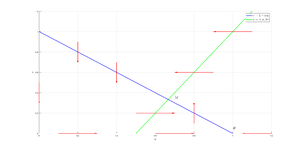
| + | [[Файл:stat_fazz_1.png|мини|Метод нуль-изоклин. Случай $$\alpha \gamma > 1$$]] | ||
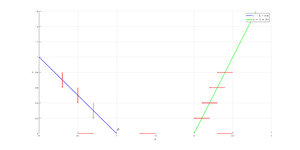
| + | [[Файл:stat_fazz_2.png|мини|Метод нуль-изоклин. Случай $$\alpha \gamma < 1$$]] | ||
| + | По графику для случая $$\alpha \gamma > 1$$ можно сделать вывод, что с течением времени система приходит в асимптотически устойчивое положение равновесия. Особая точка "похожа" на фокус. Из второго графика(случай $$\alpha \gamma < 1$$) видим, что в конечном итоге хищники вымирают, значит из биологической интерпретации этот случай нам не подходит. Для первого случая можем численно решить систему и построить фазовый портрет. | ||
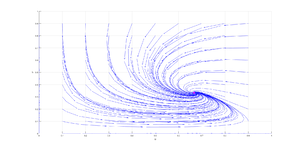
| + | [[Файл:stat_faz_3.png|мини|Фазовый портрет системы Лотки-Вольтерры с учётом внутривидовой конкуренции]] | ||
| + | При уменьшении числа жертв уменьшается число хищников, и, наоборот, при увеличении числа жертв увеличивается число хищников. Причём при достижении некоторого значения число жертв резко начинает уменьшаться. Аналогичное утверждение справедливо и для хищников. Такое поведение функции числа особей обусловлено внутривидовой конкуренцией. Полученная интерпретация удовлетворяет простейшим биологическим представлениям о взаимодействии хищников и жертв. | ||
| + | |||
| + | == Список литературы == | ||
| + | |||
| + | 1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011. | ||
| + | |||
| + | 2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2024. | ||
Версия 21:58, 6 декабря 2024
Содержание
Биологическая интерпретация характеристик системы
Модель Лотки-Вольтерры описывает взаимодействие двух видов, один из которых является хищником, а другой — жертвой. Если $$u(t)$$ — численность жертв, $$v(t)$$ — численность хищников в момент времени $$t$$, то модель имеет вид \begin{equation}\label{sys1} \begin{cases} \dot{u} = au - buv, \\ \dot{v} = - cv + duv,\\ \end{cases} \end{equation} где $$a, b, c, d > 0.$$
Рассматривая систему \ref{sys1} в качестве математической модели взаимодействующих популяций, естественно считать фазовым пространством множество $$\mathbb{R}^2_+ = \{u, v: ~ u \geq 0, v\geq 0\}$$, которое является инвариантным.
Заметим, что если отсутствуют хищники, то в математической модели \ref{sys1} популяция жертв экспоненциально растёт. Естественно изменить модель таким образом, чтобы ограничить рост жертв. Кроме того, хотя это и менее критично в рассматриваемой модели, введём слагаемое, ограничивающее рост популяции хищников. Получим: \begin{equation}\label{sys2} \begin{cases} \dot{u} = au - buv - eu^2, \\ \dot{v} = - cv + duv - fv^2, \end{cases} \end{equation} где $$a, b, c, d, e, f > 0, (u, v) \in \mathbb{R}^2_+$$.
Заметим, что \ref{sys2} отличается от \ref{sys1} последним слагаемым. Из вида этого слагаемого можно сделать вывод: чем меньше в популяции особей, тем меньше они конкурируют между собой.
Введение безразмерных переменных
Введём замену переменных $$t = T\tau, \, x = Ap\left(\tau\right), \, y = Bq\left(\tau\right)$$. Здесь $$T, A, B$$ — положительные постоянные. Далее можем записать\[\frac{d}{dt} = \frac{d}{d\tau} \cdot\frac{d\tau}{dt} = \frac{1}{T}\cdot\frac{d}{d\tau}.\] Тогда систему \ref{sys2} можно записать в виде\[\begin{cases} \frac{A}{T}\dot{p} = aAp - bApBq - eA^2p^2, \\ \frac{B}{T}\dot{q} = -cBq + dApBq - fB^2q^2. \end{cases}\] Упростим оба уравнения системы: \begin{cases} \dot{p} = aTp - bTBpq - eTAp^2, \\ \dot{q} = - cTq + dTApq - fTBq^2. \end{cases} Пусть теперь \begin{equation*} T = \frac{1}{a}, \quad B = \frac{a}{b},\quad A = \frac{a}{d}. \end{equation*} Тогда система будет выглядеть следующим образом: \begin{cases} \dot{p} = p - pq - \frac{e}{d}p^2, \\ \dot{q} = - \frac{c}{a}q + pq - \frac{f}{b}q^2. \end{cases} Обозначим \begin{equation*} \alpha = \frac{e}{d}, \quad \gamma = \frac{c}{a}, \quad \beta = \frac{f}{b}, \quad u = p, \quad v = q. \end{equation*} Тогда финальная система имеет вид: \begin{equation}\label{sys3} \begin{cases} \dot{u} = u - uv - \alpha u^2, \\ \dot{v} = -\gamma v + uv - \beta v^2, \end{cases} \quad (u, v)\in \mathbb{R}^2_+, \quad \alpha > 0,\quad \beta > 0,\quad \gamma > 0. \end{equation}
Исследование неподвижных точек и характера их устойчивости
Для нахождения особых точек системы \ref{sys3} необходимо решить следующую систему: \begin{equation}\label{ot} \begin{cases} u(1 - v - \alpha u) = 0, \\ v(-\gamma + u - \beta v) = 0. \end{cases} \end{equation} Очевидно, точка $$O(0, 0)$$ является решением.
Точка $$A(0, -\frac{\gamma}{\beta})$$ является решением системы \ref{ot}, но не лежит в $$\mathbb{R}^2_+$$, следовательно, не является точкой покоя.
Точка $$B(\frac{1}{\alpha}, 0)$$ является точкой покоя.
Последнюю точку покоя получаем как решение системы: \begin{equation*} \begin{cases} 1 - v - \alpha u = 0, \\ -\gamma + u - \beta v = 0. \end{cases} \end{equation*} Обозначим \begin{equation}\label{resh} u^\ast = \dfrac{\gamma + \beta}{1 + \alpha \beta}, \quad v^\ast = \dfrac{1 - \alpha\gamma}{1 + \alpha\beta}. \end{equation} Итак, ещё одна особая точка — $$M(u^\ast, v^\ast)$$.
Найдём матрицу Якоби для системы \ref{sys3}: \begin{equation}\label{j1} J \left(x, y\right)= \begin{pmatrix} \dfrac{\partial f_1}{\partial u} & \dfrac{\partial f_1}{\partial v} \\ \\ \dfrac{\partial f_2}{\partial u} & \dfrac{\partial f_2}{\partial v} \end{pmatrix} = \begin{pmatrix} 1 - v - 2\alpha u & -u \\ \\ v & -\gamma + u -2\beta v \end{pmatrix} \end{equation}
$$\quad\quad$$ 1. Посчитаем значения матрицы Якоби в точке $$O$$: \begin{equation*} J \left(0,0\right)= \begin{pmatrix} 1 & 0 \\ 0 & -\gamma \end{pmatrix}. \end{equation*} В данном случае собственные значения матрицы вычисляются легко: $$\lambda_1 = 1, ~ \lambda_2 = -\gamma.$$ Получили, что $$\lambda_{1, 2} \in \mathbb{R}, ~\lambda_1 \cdot \lambda_2 < 0$$, значит $$O$$ — седло по определению. Напомним, что седло — всегда неустойчивое положение равновесия.
$$\quad\quad$$ 2. Посчитаем значения матрицы Якоби в точке $$B$$: \begin{equation*} J \bigg(\dfrac{1}{\alpha},0\bigg)= \begin{pmatrix} -1 & -\dfrac{1}{\alpha} \\ 0 & -\gamma + \dfrac{1}{\alpha} \end{pmatrix}. \end{equation*} Рассмотрим характеристический многочлен полученной матрицы: \begin{equation*} \chi = \bigg(\lambda + 1\bigg)\bigg(\lambda - \bigg(\dfrac{1}{\alpha} - \gamma\bigg)\bigg) \end{equation*} Теперь можем найти собственные значения: \begin{equation*} \lambda_1 = -1, \quad \lambda_2 = \dfrac{1}{\alpha} - \gamma, \quad \lambda_{1, 2} \in \mathbb{R}. \end{equation*} Если $$\alpha \gamma < 1$$, то $$\lambda_1 \cdot \lambda_2 < 0$$, и $$B$$ — седло по определению.
Если $$\alpha \gamma > 1$, то $\lambda_2 < 0,~ \lambda_1 \cdot \lambda_2 > 0$$, и $$B$$ — устойчивый узел по определению.
$$\quad\quad$$ 3. Посчитаем значения матрицы Якоби в точке $$M$$: \begin{equation*} J \bigg(u^\ast, v^\ast\bigg)= \begin{pmatrix} -\alpha u^\ast & -u^\ast \\ v^\ast & -\beta v^\ast \end{pmatrix}. \end{equation*} Вспомним условие устойчивости особой точки для общей схемы исследования: \begin{equation} \Tr J < 0, \quad \det J > 0. \end{equation} Заметим, что при $$\alpha \gamma > 1$$ точку $$M$$ рассматривать не нужно, так как из \ref{resh}: $$~v^\ast < 0$$ и $$M \notin \mathbb{R}^2_+$$.
Тогда в нашей задаче \begin{equation*} \Tr J(u^\ast, v^\ast) = -\alpha u^\ast - \beta v^\ast < 0, \quad \det J(u^\ast, v^\ast) = u^\ast v^\ast (1 + \alpha \beta) > 0. \end{equation*} Таким, образом, $$M$$ — устойчивое положение равновесия.
Объединим все полученные выше случаи. Если $$\alpha \gamma < 1$$, то особые точки $$O, ~ B$$ неустойчивые, а $$M$$ устойчивая. Если $$\alpha \gamma > 1$$, то $$O$$ — неустойчивая особая точка, $$B$$ — устойчивый узел.
Построение фазовых портретов системы
В отличие от классической модели Лотки-Вольтерры, переменные в уравнении для траекторий не разделяются, поэтому для анализа фазового портрета применим метод нуль-изоклин. Разделим $$\mathbb{R}^2_+$$ на области прямыми \begin{equation*} v^\ast = 1 - \alpha u^\ast,\quad ~ u^\ast = \gamma + \beta v^\ast. \end{equation*} Тогда в полученных областях сможем оценить направление траекторий, тем самым построив "набросок" фазового портрета.
По графику для случая $$\alpha \gamma > 1$$ можно сделать вывод, что с течением времени система приходит в асимптотически устойчивое положение равновесия. Особая точка "похожа" на фокус. Из второго графика(случай $$\alpha \gamma < 1$$) видим, что в конечном итоге хищники вымирают, значит из биологической интерпретации этот случай нам не подходит. Для первого случая можем численно решить систему и построить фазовый портрет.
При уменьшении числа жертв уменьшается число хищников, и, наоборот, при увеличении числа жертв увеличивается число хищников. Причём при достижении некоторого значения число жертв резко начинает уменьшаться. Аналогичное утверждение справедливо и для хищников. Такое поведение функции числа особей обусловлено внутривидовой конкуренцией. Полученная интерпретация удовлетворяет простейшим биологическим представлениям о взаимодействии хищников и жертв.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2024.