Теорема Бендиксона-Пуанкаре: различия между версиями
| Строка 1: | Строка 1: | ||
== Теорема Бендиксона-Пуанкаре == | == Теорема Бендиксона-Пуанкаре == | ||
| + | === Определения === | ||
| + | |||
| + | === Точка покоя === | ||
| + | **Точка покоя** системы дифференциальных уравнений | ||
| + | \[ | ||
| + | \begin{aligned} | ||
| + | \dot{x} &= f_1(x, y), \\ | ||
| + | \dot{y} &= f_2(x, y) | ||
| + | \end{aligned} | ||
| + | \] | ||
| + | — это такая точка \((x_0, y_0) \in \mathbb{R}^2\), в которой выполняются равенства: | ||
| + | \[ | ||
| + | f_1(x_0, y_0) = 0, \quad f_2(x_0, y_0) = 0. | ||
| + | \] | ||
| + | В этой точке движение системы замирает: траектория остаётся неподвижной. | ||
| + | |||
| + | === Предельная точка === | ||
| + | **Предельная точка** траектории \(\gamma(t) = (x(t), y(t))\) системы дифференциальных уравнений — это точка \((\bar{x}, \bar{y}) \in \mathbb{R}^2\), для которой существует последовательность моментов времени \(\{t_k\}_{k=1}^\infty\), такая что: | ||
| + | \[ | ||
| + | t_k \to \infty, \quad (x(t_k), y(t_k)) \to (\bar{x}, \bar{y}), \quad \text{при } k \to \infty. | ||
| + | \] | ||
| + | |||
| + | === Мешок Бендиксона === | ||
| + | Мешок Бендиксона — это область фазового пространства, ограниченная замкнутой траекторией, внутри которой отсутствуют другие замкнутые траектории, точки покоя или бесконечные траектории. Используется для анализа поведения динамических систем в положительно инвариантных областях. | ||
| + | |||
Рассмотрим систему дифференциальных уравнений: | Рассмотрим систему дифференциальных уравнений: | ||
\[ | \[ | ||
Версия 10:42, 19 декабря 2024
Содержание
Теорема Бендиксона-Пуанкаре
Определения
Точка покоя
- Точка покоя** системы дифференциальных уравнений
\[ \begin{aligned} \dot{x} &= f_1(x, y), \\ \dot{y} &= f_2(x, y) \end{aligned} \] — это такая точка \((x_0, y_0) \in \mathbb{R}^2\), в которой выполняются равенства: \[ f_1(x_0, y_0) = 0, \quad f_2(x_0, y_0) = 0. \] В этой точке движение системы замирает: траектория остаётся неподвижной.
Предельная точка
- Предельная точка** траектории \(\gamma(t) = (x(t), y(t))\) системы дифференциальных уравнений — это точка \((\bar{x}, \bar{y}) \in \mathbb{R}^2\), для которой существует последовательность моментов времени \(\{t_k\}_{k=1}^\infty\), такая что:
\[ t_k \to \infty, \quad (x(t_k), y(t_k)) \to (\bar{x}, \bar{y}), \quad \text{при } k \to \infty. \]
Мешок Бендиксона
Мешок Бендиксона — это область фазового пространства, ограниченная замкнутой траекторией, внутри которой отсутствуют другие замкнутые траектории, точки покоя или бесконечные траектории. Используется для анализа поведения динамических систем в положительно инвариантных областях.
Рассмотрим систему дифференциальных уравнений:
\[
\begin{aligned}
\dot{x} &= f_1(x, y), \\
\dot{y} &= f_2(x, y),
\end{aligned} \quad \bar{D} \subset \mathbb{R}^2
\]
Условия:
- 1. \(\bar{D}\) — ограниченная замкнутая область в \(\mathbb{R}^2\).
- 2. \(\bar{D}\) — положительно инвариантна относительно системы:
\[
(x_0, y_0) \in \bar{D}, \quad
\left.
\begin{gathered}
x = x(x_0, y_0) \\
y = y(x_0, y_0)
\end{gathered}
\right\} \quad \gamma \subset \bar{D}
\]
- 3. в \(\bar{D}\) нет точек покоя.
Если все три условия выполняются, то в \(D\) существует по крайней мере одна замкнутая траектория (цикл).
Лемма 1
Если траектория системы содержит хотя бы одну свою предельную точку при \(t \to \infty\), то это либо точка покоя, либо цикл.
Доказательство:
Пусть содержится \(\bar{x}\) и \(t \to \infty\).
1. Если \(\bar{x}\) - точка покоя, то \(x(t) = \bar{x}\).
Иначе рассмотрим второй случай.
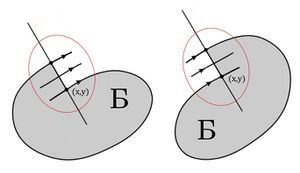
2. Рассмотрим окрестность точки \(\bar{x}\). В окрестности точки по теореме о выпрямлении векторного поля, его можно представить как пучок параллельных прямых. \(\bar{x}\) - предельная точка, то траектории будут близко к ней. Если траектория не попадает в \(\bar{x}\), то она будет оставаться в мешке Бендиксона и не будет приближаться к \(\bar{x}\). Получаем противоречие.
Лемма 2
Пусть траектория \(\gamma\) при \(t \to \infty\) имеет предельную точку \(\bar{M} \in \gamma\), принадлежащую некоторой замкнутой кривой \(\bar{\gamma}\). Тогда либо \(\gamma = \bar{\gamma}\), либо \(\gamma\) спиралевидно приближается к \(\bar{\gamma}\).
Доказательство:
1. Траектория \(\gamma\) проходит через \(\bar{M} \in \bar{\gamma}\), тогда \(x(t, \bar{M}) \in \bar{\gamma}\).
2. Если траектория проходит сколь угодно близко от \(\bar{M}\), но тогда траектория на любом обороте будет приближаться к \(\bar{M}\), так как это предельная точка.
Доказательство теоремы Бендиксона-Пуанкаре
Из произвольной точки выпускаем траекторию: \[ \gamma: \begin{cases} x = x(t, x_0), \\ y = y(t, y_0) \end{cases}, \quad (x_0, y_0) \in \bar{D}. \] Эта траектория не покидает замкнутую область \(\bar{D}\).
По теореме Вейерштрасса можно выделить последовательность \(t_k\), сходящуюся к предельной точке: \[ \begin{cases} x_k = x(t_k, x_0), \\ y_k = y(t_k, y_0) \end{cases} \rightarrow \begin{pmatrix} \bar{x} \\ \bar{y} \end{pmatrix} = \bar{M}. \]
Теперь рассматриваем два возможных случая:
1. \(\bar{M} \in \gamma\): в этом случае, по Лемме 1, \(\gamma\) является замкнутой траекторией.
2. \(\bar{M} \notin \gamma\).Тогда рассматриваем траекторию \(\bar{\gamma}\), проходящую через \(\bar{M}\):
\[
\begin{cases}
x = x(t, x_0), \\
y = y(t, y_0)
\end{cases} \quad \Rightarrow \quad \bar{\gamma}.
\]
Для этой траектории выделяем последовательность \(\{t_n\}\), сходящуюся к предельной точке.
\[ \begin{cases} x_n = x(t_n, \bar{x}), \\ y_n = y(t_n, \bar{y}) \end{cases} \rightarrow \begin{pmatrix} \bar{\bar{x}} \\ \bar{\bar{y}} \end{pmatrix} = \bar{\bar{M}}. \] Из инвариантности предельного множества следует, что \(\bar{\gamma}\) является предельным множеством, а значит, возможны два случая:
Случай \(\bar{\bar{M}} \in \bar{\gamma}\): тогда по Лемме 2 \(\bar{\gamma}\) является замкнутой траекторией.
Случай \(\bar{\bar{M}} \notin \bar{\gamma}\): Это приводит к противоречию, так как \(\bar{\bar{M}}\) и любая другая точка \(\tilde{a}\) из \(\bar{\gamma}\) одновременно не могут быть предельными.
Таким образом, доказано, что при выполнении условий теоремы траектория либо является замкнутой, либо приводит к противоречию.
Пример
Рассмотрим систему уравнений: \[ \begin{cases} \dot{x} = y, \\ \dot{y} = -x \end{cases} \] Траектории системы лежат на окружностях вида \(x^2 + y^2 = R^2\). Условия теоремы выполнены, но предельного цикла нет.
Практическое применение
Теорема Бендиксона-Пуанкаре имеет широкое применение в различных областях, где исследуются динамические системы с ограничениями и колебательными процессами. Она помогает предсказать наличие устойчивых циклических решений в сложных системах. Рассмотрим несколько примеров её применения:
1. Биологические популяции
Один из наиболее известных примеров — модель взаимодействия хищников и жертв, известная как модель Лотки-Вольтерры. Эта модель описывает динамику двух популяций: хищников и их жертв. В частности, она формулируется как система дифференциальных уравнений:
\[ \begin{cases} \dot{x} = \alpha x - \beta xy, \\ \dot{y} = \delta xy - \gamma y \end{cases} \]
где: - \(x\) — численность популяции жертв, - \(y\) — численность популяции хищников, - \(\alpha\), \(\beta\), \(\delta\), \(\gamma\) — положительные константы, характеризующие взаимодействие между популяциями.
Теорема Бендиксона-Пуанкаре утверждает, что если система не имеет точек покоя в области фазового пространства, то существуют замкнутые траектории (циклические колебания). Это соответствует колебаниям численности хищников и жертв, когда численности обеих популяций периодически увеличиваются и уменьшаются. Важно, что теорема позволяет установить существование устойчивых циклов, что даёт понимание долгосрочного поведения экосистемы.
2. Электрические цепи
Теорема Бендиксона-Пуанкаре находит применение и в области электрических цепей, особенно при анализе непрямолинейных колебательных процессов. Например, в цепях с нелинейными элементами, такими как диоды или транзисторы, часто наблюдаются устойчивые периодические колебания. Эти колебания могут быть описаны дифференциальными уравнениями, аналогичными тем, что возникают в биологических моделях.
Одним из классических примеров является модель цепи с нелинейным сопротивлением, описанная системой уравнений:
\[ \begin{cases} \dot{x} = y, \\ \dot{y} = -x + f(x), \end{cases} \]
где \(f(x)\) — нелинейная функция, представляющая характеристики нелинейного сопротивления. Теорема Бендиксона-Пуанкаре предсказывает, что в таких системах, если отсутствуют точки покоя и система положительно инвариантна, то возможны устойчивые замкнутые траектории, которые соответствуют периодическим колебаниям напряжения или тока в цепи.
Эти колебания могут быть использованы в различных электронных устройствах, таких как генераторы и осцилляторы, для создания стабильных и предсказуемых периодических сигналов.
Следствие
Если в окрестности замкнутой траектории \(\bar{\gamma}\) отсутствуют другие замкнутые траектории, то все траектории, начинающиеся вблизи \(\bar{\gamma}\), спиралевидно стремятся к \(\bar{\gamma}\).
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2024.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.