Модель взаимодействия видов Гаузе. Принцип Гаузе

Модель взаимодействия видов Гаузе

Рассмотрим межпопуляционное отношение конкуренции между двумя видами. Предполагается, что оба вида являются автотрофами, т. е. способны размножаться независимо друг от друга. В модели Лотки—Вольтерры такой способностью обладали лишь жертвы, а способность к размножению хищников была связана с наличием жертв. Полагаем, что в изоляции динамика популяции обоих видов подчиняется логистическому уравнению (в биологических терминах — в популяциях существует внутривидовая конкуренция), а взаимно отрицательное влияние пропорционально численности видов. Математической моделью описанной ситуации является следующая система: \begin{equation} \dot{N_1} = r_1 N_1 \left ( 1 - \dfrac{N_1}{K_1} \right ) - a N_1 N_2, \\ \dot{N_2} = r_2 N_2 \left ( 1 - \dfrac{N_2}{K_2} \right ) - b N_1 N_2. \end{equation} Здесь $$N_1$$ и $$N_2$$ — текущие численности видов, а $$K_1$$ и $$K_2$$ — их предельные численности.

В безразмерных переменных система принимает вид \begin{equation} \dot{u} = u(1 - v - \alpha u), \\ \dot{v} = v(\gamma - u - \beta v). \end{equation}

В области $$\mathbb{R}^2_+$$ всегда существуют положения равновесия \begin{equation} A_1 = (0, \, 0), \ A_2 = (\alpha^{-1}, \, 0), \ A_3 = (0, \gamma \beta^{-1}). \end{equation} Кроме того, если $$\alpha \beta > 1$$, $$\alpha \gamma > 1$$, $$\beta > \gamma$$ или $$\alpha \beta < 1$$, $$\alpha \gamma < 1$$, $$\beta < \gamma$$, то в $$R^2_+$$ существует положение равновесия \begin{equation} A_4 = (u^*, \, v^*) = ((\beta - \gamma)(\alpha \beta - 1)^{-1}, \, (\alpha \gamma - 1)(\alpha \beta - 1)^{-1}). \end{equation} Матрица Якоби системы (*) имеет вид \begin{equation} J(u, \, v) = \begin{bmatrix} 1 - 2 \alpha u - v & -u \\ -v & \gamma - u - 2 \beta v \end{bmatrix}. \end{equation} Положение равновесия $$A_1$$ — неустойчивый узел (собственные числа равны $$1$$ и $$\gamma$$); $$A_2$$ — седло, если $$\beta > \gamma$$ и устойчивый узел, если $$\beta < \gamma$$. Если $$A_4 \in \mathbb{R}^2_+$$, то \begin{equation} \tr J(u^*, \, v^*) = -(\alpha u^* + \beta v^*) < 0, \\ \det J(u^*, \, v^*) = (\alpha \beta - 1) u^* v^*. \end{equation}

Анализ параметрического портрета

Рис. 1. Параметрический портрет системы (2)

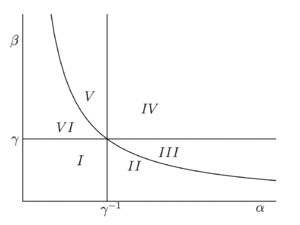
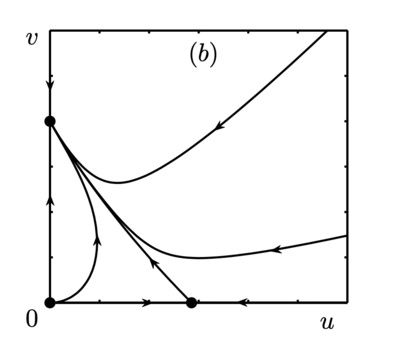
Удобно изобразить линии, на которых происходит смена устойчивости положений равновесия, на параметрическом портрете (рис. 1). В областях II и III фазовые портреты топологически эквивалентны, все траектории стремятся к асимптотически устойчивому положению равновесия $$A_3$$ (рис. (b)). Ситуация аналогична для областей V и VI с тем отличием, что орбиты системы (2) стремятся к $$A_2$$. Оба этих случая характеризуются доминированием одного из конкурирующих видов и неизбежным вымиранием второго.

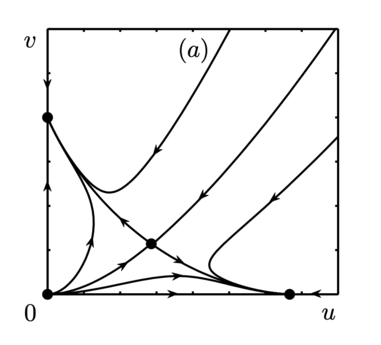
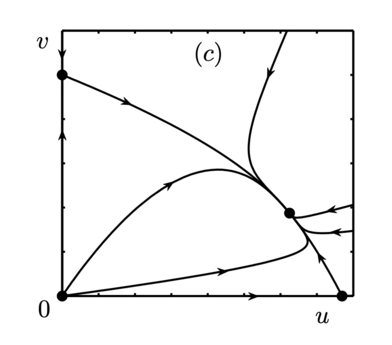
В области I реализуется бистабильная ситуация (рис. (a)). Положение равновесия $$A_4 \in \mathbb{R}^2_+$$ неустойчиво (седловая точка), а $$A_2$$ и $$A_3$$ — устойчивые узлы. В зависимости от начальных условий может доминировать как первый вид, так и второй. Во всех указанных выше случаях один из видов в процессе эволюции вымирает. Ситуация становится принципиально иной в области IV. Положение равновесия $$A_4 \in \mathbb{R}^2_+$$ в этой области асимптотически устойчиво (устойчивый узел), остальные положения равновесия неустойчивы (рис. (c)).

• 
• 
• 

Как показывает рис. 1, из шести областей значений параметров модели (2) только в одной происходит сосуществование конкурирующих видов. Многочисленные наблюдения и исследования показывают, что данная ситуация оказывается общей — практически всегда один из конкурирующих видов подавляет другой. Одним из первых математически точно сформулировал этот принцип (закон конкурентного исключения) Георгий Францевич Гаузе в своей работе «Борьба за существование».

Принцип Гаузе

Согласно принципу Гаузе, два вида, занимающие одну экологическую нишу, не могут устойчиво сосуществовать друг с другом. Докажем закон Гаузе как математиское утверждение в рамках предложенной математической модели.

Утверждение. Если $$n$$ полуляций линейно зависят от $$m$$ ресурсов, причем $$m < n$$, то по крайней мере одна из популяций вымирает.

Доказательство. Предположение о линейной зависимости от ресурсов критично для приведенного утверждения. Оно означает, что коэффициент скорости роста i-й популяции имеет вид \begin{equation} \dfrac{\dot{u_i}}{u_i} = b_{i1} R_1 + \dots + b_{im} R_m - \alpha_i, \ i = 1, \, \dots, \, n. \end{equation} Постоянные $$\alpha_i$$ показывают скорость вымирания в отсутствие ресурсов. $$R_k$$ — это изобилие k-го ресурса, а коэффициенты $$b_{ik}$$ описывают эффективность i-го вида использовании k-го ресурса. Изобилие k-го ресурса зависит от плотностей популяций. Если эта зависимость линейна, то в качестве выражений для $$R_k$$ можно взять \begin{equation} R_k = \overline{R_k} - \sum{u_i a_{ki}} \end{equation} с положительными постоянными $$\overline{R_k}$$ и $$a_{ki}$$. Последнее предположение задает систему дифференциальных уравнений в явном виде, но для доказательства не потребуется. Достаточно допустить, что ресурсы могут быть исчерпаны. Другими словами, плотности $$u_i$$ не могут расти до бесконечности.

Так как $$n > m$$, система уравнений \begin{equation} \sum_{i = 1}^n{c_i b_{ij}} = 0, \ j = 1, \, \dots, \, m \end{equation} имеет нетривиальное решение $$(c_1, \, \dots, \, c_n)$$. Пусть \begin{equation} \alpha = \sum_{i = 1}^n{c_i \alpha_i} \neq 0 \end{equation} (этого всегда можно добиться, если $$n > m + 1$$).

Рассмотрим общий случай $$\alpha > 0$$. Так как наряду с решением $$(c_1, \, \dots, \, c_n)$$ пригодно решение $$(-c_1, \, \dots, \, -c_n)$$, мы можем считать, что $$\alpha > 0$$. Из (5.7 в Братусе) получим \begin{equation} \sum{c_i \dfrac{d}{dt}(ln u_i)} = \sum{c_i \dfrac{\dot{u_i}}{u_i}} = -\alpha. \end{equation}

Интегрируя от $$0$$ до $$T$$, получим \begin{equation} \prod_{i = 1}^n{(u_i(T))^{c_i}} = C e^{-\alpha T} \end{equation} для некоторой постоянной $$C$$. Если $$T \to \infty$$, правая часть последнего выражения сходится к нулю. Так как все $$u_i$$ ограничены, должен существовать по крайней мере один индекс $$i$$ такой, что $$\lim \inf_{T \to \infty} u_i(T) = 0$$, что и означает вымирание соответствующего вида.

Применимость к биологическим моделям

Слово «закон» в применении к экологическим системам не должно трактоваться в точном математическом смысле. Хотя закон конкурентного исключения в настоящее время является общепринятым, все же существуют ситуации, когда его необходимо корректировать. Например, в верхних слоях водной толщи нередко сосуществуют несколько десятков видов планктонных водорослей, а число факторов, ограничивающих рост их популяций, очень невелико, что противоречит закону Гаузе. Объяснение этого феномена было предложено Хатчинсоном (George Evelyn Hutchinson, 1903–1991, американский зоолог и иммунолог, известный также многочисленными применениями математических моделей в биологии), который предположил, что планктонное сообщество находится в неравновесном состоянии: одни виды не вытесняют другие окончательно, так как постоянно меняются внешние условия, а в новых условиях преимущество получают совсем другие виды.

Список литературы

1. Абрамова В.В. «Лекции по динамическим системам и биоматематике», 2024.
2. Братусь А. С., Новожилов А. С., Платонов А. П. «Динамические системы и модели биологии», 2011.