Классификация особых точек в двумерном пространстве

Постановка задачи

Рассмотрим линейную систему с постоянными вещественными коэффициентами относительно вектор-функции $$\overline{y}(t) = (y_1(t), y_2(t))^T$$ \begin{equation} \label{sist1} \dfrac{d\overline{y}}{dt} = A\overline{y}, \ \ A = \left(\ \begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22}\\ \end{array}\right) . \end{equation} Нас будут интересовать фазовые $$($$то есть в плоскости $$(y_1,y_2))$$ траектории системы (\ref{sist1}). Заметим, что фазовые траектории этой системы являются интегральными кривыми обыкновенного дифференциального уравнения, полученного после исключения переменной $$t$$ из (\ref{sist1}) \begin{equation} \label{sist2} \dfrac{dy_1}{dy_2} = \dfrac{a_{11}y_1+a_{12}y_2}{a_{21}y_1+a_{22}y_2} . \end{equation} Точка покоя $$(0,0)$$ является особой для для уравнения (\ref{sist2}), поскольку в ней нарушены условия теоремы существования и единственности решения задачи Коши. Поэтому через точку $$(0,0)$$ может проходить как несколько фазовых кривых, так и ни одной. Таким образом, точка покоя $$(0,0)$$ исходной системы (\ref{sist1}) является особой точкой уравнения (\ref{sist2}) в фазовых переменных.

Классификацию точек покоя будем проводить в зависимости от собственных значений и собственных векторов матрицы $$A$$. В рассматриваемом случае $$n=2$$ имеется два собственных значения $$\lambda_1, \lambda_2$$. Если $$\lambda_1 \neq \lambda_2,$$ то соответствующие собственные векторы \[ \overline{h_1} = \left(\ \begin{array}{ccc} h_{11} \\ h_{21}\\ \end{array}\right), \] \[ \overline{h_2} = \left(\ \begin{array}{ccc} h_{12} \\ h_{22}\\ \end{array}\right). \] линейно независимы и составляют базис в $$\mathbb{C}^{2}$$. Если $$\lambda_1 = \lambda_2,$$ то возможно существование как двух, так и одного линейно независимого собственного вектора. В последнем случае существует один присоединенный вектор, линейно независимый с собственным. Рассмотрим типы точек покоя в случае невырожденной матрицы $$A$$ $$(\mathrm{det} A \neq 0)$$.

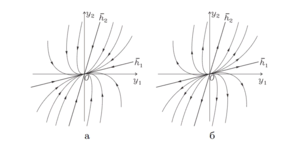
Узел $$(\lambda_1, \lambda_2 \in \mathbb{R}, \ \ \lambda_1 \neq \lambda_2, \ \ \lambda_1 \cdot \lambda_2 > 0)$$

Общее решение системы (\ref{sist1}) имеет вид \begin{equation} \label{sist3} y(t) = \begin{pmatrix} y_1(t) \\ y_2(t) \end{pmatrix} = С_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t} + С_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}, \ \ \forall C_1, C_2 \in \mathbb{R}. \end{equation}

Рассмотрим сначала случай, когда собственные значения отрицательны: $$\lambda_2 < \lambda_1 < 0.$$ Тогда нулевая точка покоя асимптотически устойчива по Ляпунову и называется устойчивым узлом. Фазовые кривые при $$t \rightarrow +\infty$$ стремятся к устойчивому узлу: $$\overline{y}(t) \rightarrow \overline{\Theta}$$. Выясним, по какому направлению фазовые траектории входят в узел. Для этого вычислим производную \begin{equation} \label{sist4} \dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{\lambda_1t} + C_2h_{12}\lambda_2e^{\lambda_2t}}{C_1h_{21}\lambda_1e^{\lambda_1t} + C_2h_{22}\lambda_2e^{\lambda_2t}} = \dfrac{C_1h_{11}\lambda_1 + C_2h_{12}\lambda_2e^{(\lambda_2 - \lambda_1)t}}{C_1h_{21}\lambda_1 + C_2h_{22}\lambda_2e^{(\lambda_2 - \lambda_1)t}}. \end{equation} Так как $$\lambda_2 - \lambda_1 < 0,$$ то при $$C_1 \neq 0$$ имеем $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac{h_{11}}{h_{21}}$$ при $$t \rightarrow +\infty$$, то есть касательный вектор фазовой траектории в пределе коллинеарен собственному вектору $$\overline{h_1}$$. Если же $$C_1 = 0$$, то \[ \overline{y}(t) = C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix} e^{\lambda_2t}. \] Значит, фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h}_2$$, и приближается к точке покоя при $$t \rightarrow +\infty$$.

Фазовые траектории узла: а - устойчивый, б - неустойчивый

Выясним направление фазовых траекторий при $$t \rightarrow -\infty$$. В этом случае фазовые траектории, отличные от точки покоя, стремятся к бесконечно удаленной точке. В силу (\ref{sist3}) при $$C_2 \neq 0$$ имеем \[ \dfrac{dy_1}{dy_2} = \dfrac{C_1h_{11}\lambda_1e^{(\lambda_1-\lambda_2)t} + C_2h_{12}\lambda_2}{C_1h_{21}\lambda_1e^{(\lambda_1-\lambda_2)t} + C_2h_{22}\lambda_2} \rightarrow \dfrac{h_{12}}{h_{22}}, \ \ t \rightarrow -\infty, \ \ (\lambda_1 - \lambda_2 > 0), \] то есть траектории в окрестности бесконечно удаленной точки выстраиваются параллельно вектору $$\overline{h_2}$$. Если же $$C_2 = 0$$, то \[ \overline{y}(t) = C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} e^{\lambda_1t}, \] и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$.

Для положительных собственных значений $$0 < \lambda_1 < \lambda_2$$ точка покоя называется неустойчивым узлом, расположение и вид траекторий остаются теми же, что и для отрицательных собственных значений, но направление движения по траекториям меняется на противоположное.

Полезно помнить правило узла: фазовые траектории входят в узел, касаясь собственного вектора с наименьшим по модулю собственным значением.

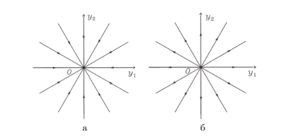
Дикритический узел $$(\lambda_1 = \lambda_2 \neq 0, \ \ \mathrm{dim \, ker}(A - \lambda_1E) = 2)$$

Фазовые траектории дикритического узла: a - устойчивый, б - неустойчивый

В случае дикритического узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечают два линейно независимых собственных вектора $$\overline{h_1}$$ и $$\overline{h_2}$$ матрицы $$A$$. Тогда выражение $$(\ref{sist3})$$ для общего решения принимает вид \[ \overline{y}(t) = (C_1\overline{h_1} + C_2\overline{h_2})e^{\lambda t} \] и определяет на плоскости $$(y_1, y_2)$$ совокупность всевозможных лучей. Выделяют два типа дикритических узла: устойчивый дикритический узел, если лучи входят в точку покоя для $$\lambda < 0$$, при $$t \rightarrow +\infty$$, и неустойчивый дикритический узел, если лучи выходят из точки покоя для $$\lambda > 0$$ , при $$t \rightarrow +\infty$$.

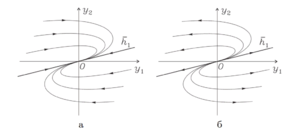
Вырожденный узел $$(\lambda_1 = \lambda_2 \neq 0,\ \ \mathrm{dim \, ker}(A-\lambda_1E) = 1)$$

Фазовые траектории вырожденного узла: а - устойчивый, б - неустойчивый

Вырожденный узел устойчив, если $$\lambda_1 = \lambda_2 < 0$$, и неустойчив, если $$\lambda_1 = \lambda_2 > 0$$. В случае вырожденного узла двукратному собственному значению $$\lambda = \lambda_1 = \lambda_2$$ отвечает один собственный вектор $$\overline{h_1}$$ матрицы $$A$$ и один присоединенный вектор $$\overline{p_1}$$. Общее решение системы (\ref{sist1}) записывается в виде \[ \overline{y}(t) = C_1\overline{h_1}e^{\lambda t} + C_2(\overline{p_1} + t\overline{h_1})e^{\lambda t}. \] Если $$C_2 = 0$$, то фазовые траектории решения $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda t}$$ состоят из двух лучей, входящих в точку покоя для $$\lambda < 0$$ (выходящих из точки покоя для $$\lambda > 0$$) при $$t \rightarrow +\infty$$ по направлению собственного вектора.

Если $$C_2 \neq 0$$, то \[ \overline{y}(t) = te^{\lambda t}(C_2\overline{h_1} + \overline{o}(1)), \ \ t \rightarrow +\infty. \] Видно, что решение касается собственного вектора в точке покоя при $$t \rightarrow +\infty$$ для $$\lambda < 0$$, либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$. На бесконечности при $$t \rightarrow +\infty$$ для $$\lambda < 0$$ либо при $$t \rightarrow -\infty$$ для $$\lambda > 0$$ фазовая траектория опять выстраивается по направлению собственного вектора, но в противоположном направлении благодаря смене знака множителя $$t$$.

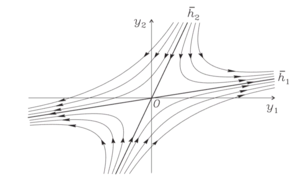
Седло $$(\lambda_1,\lambda_2 \in \mathbb{R},\ \ \lambda_2 < 0 < \lambda_1)$$

Фазовые траектории седла.

Ясно, что седло является неустойчивой точкой покоя. Воспользуемся для анализа поведения траекторий формулой (\ref{sist3}). Для $$C_1 \neq 0 $$ при $$t \rightarrow +\infty$$ получаем представление \[ \overline{y}(t) = e^{\lambda_1 t}\left(C_1 \begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + C_2 \begin{pmatrix} h_{12} \\ h_{22} \end{pmatrix}e^{(\lambda_2-\lambda_1)t}\right) = e^{\lambda_1t}\left(C_1\begin{pmatrix} h_{11} \\ h_{21} \end{pmatrix} + \overline{o}(1)\right). \] Кроме того, из (\ref{sist4}) нетрудно видеть, что $$\dfrac{dy_1}{dy_2} \rightarrow \dfrac {h_{11}}{h_{21}}$$, то есть фазовые траектории при $$t \rightarrow +\infty$$ стремятся к бесконечно удаленной точке и имеют асимптоту, задаваемую собственным вектором $$\overline{h_1}$$. Если же $$C_1 = 0$$, то $$\overline{y}(t) = C_2\overline{h_2}e^{\lambda_2t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_2}$$, приближаясь к точке покоя при $$t \rightarrow +\infty$$.

Для $$t \rightarrow -\infty$$ картина противоположная: фазовые траектории стремятся к бесконечно удаленной точке при $$C_2 \neq 0$$ и имеют асимпоту, задаваемую вектором $$\overline{h_2}$$. Если $$C_2 = 0$$, то $$\overline{y}(t) = C_1\overline{h_1}e^{\lambda_1t}$$, и фазовая траектория лежит на прямой, задаваемой собственным вектором $$\overline{h_1}$$, приближаясь к точке покоя при $$t \rightarrow -\infty$$.

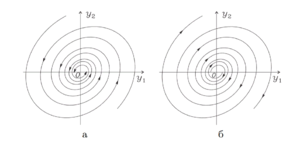
Фокус $$(\lambda_{1,2} = \delta \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0, \ \ \delta \neq 0)$$

Фазовые траектории фокуса: а - устойчивый, б - неусточивый

Точка покоя называется фокусом, если матрица $$A$$ имеет комплексно сопряженные собственные значения с ненулевыми действительной и мнимой частями. Пусть $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ $$—$$ собственный вектор с линейно независимыми $$\overline{h_{1,2}}$$, отвечающи1 собственному значению $$\lambda_1 = \delta + i\omega$$. Тогда действительная и мнимая части комплекснозначной вектор-функции $$\overline{z} = \overline{h}e^{\lambda_1t}$$ составляют вещественную фундаментальную систему решений системы \[ \left\{ \begin{array}{ccc} \overline{y_1}(t) = \mathrm{Re}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\cos{\omega t} - \overline{h_2}\sin{\omega t}), \\ \overline{y_2}(t) = \mathrm{Im}(\overline{z}(t)) = e^{\delta t}(\overline{h_1}\sin{\omega t} + \overline{h_2}\cos{\omega t}).\\ \end{array} \right. \] Поэтому общее вещественное решение имеет вид \[ \overline{y}(t) = C_1\overline{y_1}(t) + C_2\overline{y_2}(t) = e^{\delta t}(C_2\sin{\omega t} + C_1\cos{\omega t})\overline{h_1} + e^{\delta t}(C_2\cos{\omega t} - C_1\sin{\omega t})\overline{h_2}. \] Обозначая $$C = \sqrt{{C_1}^2 + {C_2}^2} \neq 0$$ и вводя вспомогательный угол $$\psi$$ из условий \[ \sin{\psi} = \dfrac{C_1}{C}, \ \ \cos{\psi} = \dfrac{C_2}{C}, \] приходим к разложению решения по базису, составленному из векторов $$\overline{h_1}$$ и $$\overline{h_2}$$ \[ \overline{y}(t) = \xi_1(t)\overline{h_1} + \xi_2(t)\overline{h_2}. \] Коэффициенты разложения определяются из соотношений \[ \xi_1(t) = Ce^{\delta t}\sin{(\omega t + \psi)},\ \ \xi_2(t) = Ce^{\delta t}\cos{(\omega t + \psi)}, \] задающих логарифмическую спираль. Выделяют два типа фокусов: устойчивый фокус $$—$$ фокус, при котором логарифмическая спираль при $$t \rightarrow +\infty$$ скручивается для $$\delta < 0$$, и неустойчивый фокус $$—$$ фокус, при котором логарифмическая спираль раскручивается для $$\delta > 0$$ .

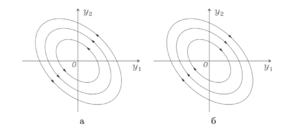
Центр $$(\lambda_{1,2} = \pm i\omega \in \mathbb{C}, \ \ \omega \neq 0)$$

Фазовые траектории центра.

Точка покоя называется центром, если матрица $$A$$ имеет чисто мнимые комплексно сопряженные собственные значения. Таким образом, центр $$—$$ устойчивая по Ляпунову точка покоя, не являющаяся асимптотически устойчивой. С помощью комплекснозначного собственного вектора $$\overline{h} = \overline{h_1} + i\overline{h_2}$$ с линейно независимыми вещественными составляющими \overline{h_1} и \overline{h_2} аналогично случаю фокуса запишем общее решение в виде разложения $$\overline{y}(t) = \xi_1(t)\overline{h_1} + \xi_2(t)\overline{h_2}$$ с коэффициентами \[ \xi_1(t) = C\sin{(\omega t + \psi)},\ \ \xi_2(t) = C\cos{(\omega t + \psi)}, \] удовлетворяющими равенству $$\xi_1^2(t) + \xi_2^2(t) = C^2$$. Тогда вектор коэффициентов $$(\xi_1(t), \xi_2(t))$$ описывает периодическое движение по окружности.

Список литературы

1. Денисов А.М., Разгулин А.В. "Обыкновенные дифференциальные уравнения", 2009.
2. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.