Преобразование Лапласа

Преобразование Лапласа — интегральное преобразование, связывающее функцию $$F(p)$$ комплексного переменного (изображение) с функцией $$f(t)$$ вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.

Определение

Прямое преобразование

Преобразованием Лапласа действительнозначной функции $$f(t)$$ называется функция $$F(p)$$ комплексной переменной такая, что

\begin{equation}\label{intLapl} \boxed{F(p) = \int\limits^{+\infty}_0 f(t) e^{-pt} dt, \quad p \in \mathbb(C).} \end{equation}

Правая часть этого выражения называется интегралом Лапласа.

Для преобразования Лапласа используется обозначение $$f(t) \supset F(t)$$

Выясним, при каких условиях существует интеграл Лапласа для заданной функции $$f(t)$$. Будем рассматривать функцию $$f_\mu(t) = e^{-\mu t} f(t)$$, $$\mu \in \mathbb{R}$$. Пусть существуют константы $$A$$, $$\mu_0$$ такие, что $$|f(t)| \le Ae^{-\mu_0 t}$$ $$\forall t\ge T$$. Тогда для любого $$\mu \ge \mu_0$$ $$\exists \int\limits_0^{+\infty} |e^{-\mu t} f(t)|dt < \infty$$. Поставим в соответствие функции $$f_\mu(t)$$ функцию $$F_\mu(t)$$, определяемую как прямое преобразование Фурье функции $$f_\mu(t)$$: $$F_\mu(t) = \int\limits_0^{+\infty} f_\mu(t) e^{-i\omega t} dt = \int\limits_0^{+\infty} f(t) e^{-\mu t} e^{-i\omega t} dt = \left\{\text{обозначим } p = \mu + i\omega\in \mathbb{C}\right\} = \int\limits_0^{+\infty} f(t) e^{-pt} dt \equiv F(p)$$.

Получаем следующие достаточные условия существования прямого преобразования Лапласа:

1. функция $$f$$ растёт не быстрее показательной функции, т.е.

\begin{equation}\label{growth_cond} \exists A, \mu_0 \text{ такие, что } |f(t)|\le Ae^{-\mu_0 t} \quad \forall t\ge T \end{equation}

1. интеграл $$\int\limits_0^{+\infty}|f(t) dt|$$ существует и конечен.

Обратное преобразование

Будем рассматривать физически реализуемую функцию $$\chi(t)f_\mu(t)$$, где функция $$\chi(t)$$ — функция Хевисайда: \[ \chi(t) = \left\{\begin{align*} 1,\ &t\ge0,\\ 0,\ &t<0. \end{align*}\right. \]

В этом случае $$t$$ может иметь смысл времени, поэтому получаем, что функция $$f(t)\chi(t)$$ задана только на положительной полуоси $$t\ge0$$.

Рассмотрим обратное преобразование Фурье от функции $$F_\mu(\omega)$$: \[ f(t) e^{-\mu t} \chi(t) = f_\mu(t) \chi(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F_\mu(\omega) e^{i\omega t} dt = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F(p) e^{i\omega t} dt. \]

Сделаем замену $$p = \mu + i\omega$$. Тогда $$d\omega = \frac{dp}{i}$$, а верхний и нижний пределы интегрирования равны: $$\omega = +\infty \Rightarrow p = \mu + i\infty$$, $$\omega = -\infty \Rightarrow p = \mu - i\infty$$. Получаем:

\[ f(t) e^{-\mu t} \chi(t) = \frac{1}{2\pi i} e^{-\mu t} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p) e^{pt} dp \quad \forall \mu > \tilde{\mu}. \]

Домножив обе части равенства на $$e^{\mu t}$$, окончательно получим формулу обратного преобразования Лапласа:

\begin{equation}\label{Mellins_formula} \boxed{f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p)e^{pt} dp.} \end{equation}

Правая часть этого выражения называется формулой Меллина.

Теорема об области существовании изображения

Область существования изображения.

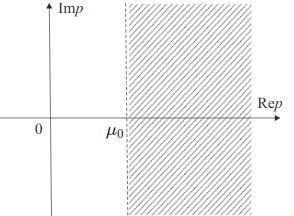
Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости \(\mathrm{Re} p > \mu_0\) и является в этой области аналитической функцией.

Доказательство. Докажем, сначала, что интеграл Лапласа \eqref{intLapl} сходится абсолютно в области $$\mathrm{Re} p = \mu > \mu_0$$. В силу общего признака сравнения и условия роста \eqref{growth_cond} получаем, что

\[ \left|\int\limits_0^{+\infty} f(t) e^{pt} dt\right| \le \int\limits_0^{+\infty} |f(t)| e^{-\mu t} dt < A \int\limits_0^{+\infty} e^{-(\mu-\mu_0)t} dt. \]

Итак, для $$\mu>\mu_0$$: \begin{equation}\label{int_bounds} \left| \int\limits_0^{+\infty} f(t) e^{-pt} dt \right| < \frac{A}{\mu-\mu_0}, \end{equation} то есть интеграл Лапласа сходится абсолютно.

Докажем теперь существование производной несобственного интеграла \eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$\mathrm{Re}\,p > \mu_0$$ интеграла \[ F'(p) = J(p) = \int\limits_0^{+\infty} (-t) f(t) e^{(\mu + i\omega)t} dt \]

Выберем произвольное положительное действительное число $$\mu_1$$ такое, что $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. Тогда, в соответствии с признаком Вейерштрасса равномерной сходимости получаем, что

\[ |J(p)| \le \int\limits_0^{+\infty} t |f(t)| e^{-\mu_1 t} dt < A\int\limits_0^{+\infty} t e^{-(\mu_1-\mu_0)t} dt = \frac{A}{(\mu_1-\mu_0)^2} < \infty, \]

что и доказывает возможность дифференцирования интеграла \eqref{intLapl} по параметру $$p$$ в области $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. В силу произвольности выбора $$\mu_1$$ мы доказали аналитичность изображения в области $$\mathrm{Re}\,p > \mu_0$$. $$\blacksquare$$

Замечание. Из неравенства \eqref{int_bounds} вытекает, что $$\lim\limits_{\mu \to +\infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)\to 0$$ при $$p \to \infty$$, оставаясь внутри угла $$-\frac{\pi}{2} + \delta < \arg p < \frac{\pi}{2} - \delta$$, где $$\delta$$ — сколь угодно малое положительное число. Если же функция $$F(p)$$ аналитична в бесконечно удалённой точке $$p=\infty$$, то $$F(p)\to\infty$$ при $$p\to\infty$$ по любому пути.

Элементарные преобразования

$$f(t) \chi(t)$$	$$F(t)$$
\[1\]	\[\frac{1}{p}\]
\[ e^{\beta t} \]	\[ \frac{1}{p-\beta} \]
\[ f(t)e^{\beta t} \]	\[ F(p-\beta) \]
\[ f(t)e^{-\beta t} \]	\[ F(\beta-p) \]
\[ t^\alpha e^{\beta t} \]	\[ \frac{\Gamma(\alpha + 1)}{(p-\beta)^{\alpha + 1}} \]
\[ t^n, n\in\mathbb{N} \]	\[ \frac{n!}{p^{n+1}} \]
\[ t^\alpha, \alpha\in\mathbb{R} \]	\[ \frac{\Gamma(\alpha+1)}{p^{\alpha+1}} \]
\[ \sin \beta t \]	\[ \frac{\beta}{p^2+\beta^2} \]
\[ \cos \beta t \]	\[ \frac{p}{p^2+\beta^2} \]
\[ t^\alpha \sin \beta t \]	\[ \frac{\Gamma(\alpha + 1)}{2i}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} - \frac{1}{(p + i\beta)^{\alpha+1}} \right) \]
\[ t^\alpha \cos \beta t \]	\[ \frac{\Gamma(\alpha + 1)}{2}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} + \frac{1}{(p + i\beta)^{\alpha+1}} \right) \]
\[ \sinh t \]	\[ \frac{\beta}{p^2-\beta^2} \]
\[ \cosh t \]	\[ \frac{p}{p^2-\beta^2} \]
\[ t^\alpha \sinh t \]	\[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} - \frac{1}{(p+\beta)^{\alpha + 1}} \right) \]
\[ t^\alpha \cosh t \]	\[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} + \frac{1}{(p+\beta)^{\alpha + 1}} \right) \]
\[ \delta \]	\[ 1 \]

Приведём доказательства для некоторых из этих формул.

1. Пусть $$f(t)=1$$.
   \[ \int\limits_0^{+\infty} t e^{-pt} dt = \left. -\frac{1}{p} e^{-pt} \right|^{+\infty}_0 = \frac{1}{p}. \]
   Легко видеть, что данный интеграл сходится при любом $$\mu>0$$
2. Пусть теперь $$f(t) \supset F(p)$$.
   \[ \int\limits_0^{+\infty} f(t) e^{(\beta-p)t} dt = F(p-\beta). \]
3. Найдём преобразование Лапласа для функции $$f(t) = \chi(t) t^\alpha$$, $$\alpha > 0$$.
   \[ \forall p\in\mathbb{R} : \int\limits_0^{+\infty} t^\alpha e^{-\pt} dt = \left\{ \begin{matrix} pt = s \\ ds = pdt \end{matrix} \right\} = \int\limits_0^{+\infty} \left( \frac{s}{p} \right)^\alpha e^{-s} \frac{1}{p} ds = \frac{1}{p^{\alpha + 1}} \int\limits_0^{+\infty} s^\alpha e^{-s} ds = \frac{1}{p^{\alpha + 1}} \Gamma(\alpha + 1). \]
   Эту функцию можно аналитически продолжить на всю комплексную плоскость, т.е. \[ \forall p\in\mathbb{C} : \chi(t) t^\alpha \supset \frac{\Gamma(\alpha + 1)}{p^{\alpha + 1}} \quad \forall \alpha > 0. \]
4. Рассмотрим функции $$\chi(t) t^\alpha \cos \beta t$$ и $$\chi(t) t^\alpha \sin \beta t$$. По формуле Эйлера: \[ \cos \beta t = \frac{e^{i\beta t} + e^{-i\beta t}}{2}, \quad \sin \beta t = \frac{e^{i\beta t} - e^{-i\beta t}}{2} \]
   Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций.
   Аналогично выводятся формулы для гиперболических тригонометрических функций: \[ \sinh x = \frac{e^x - e^{-x}}{2}, \quad \cosh x = \frac{e^x + e^{-x}}{2} \]

Вычисление обратного преобразования Лапласа

.

Рассмотрим формулу Меллина \eqref{Mellins_formula}: \[ f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp \]

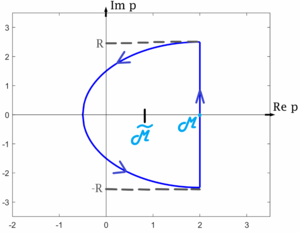
В области $$\mu > \mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, \dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} \overset{\Omega_R}{\underset{\R \to +\infty}{\rightrightarrows}} 0$$. Отсюда получаем: \[ f(t)\chi(t) = \frac{1}{2\pi i } \cdot 2\pi i \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) = \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) \]

Свойства преобразования Лапласа

Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд.

Линейность

Для любых $$\alpha,\ \beta \in \mathbb{C}$$ справедливо:

\[ \alpha f(t) + \beta g(t) \supset \alpha F(p) + \beta G(p). \]

Это соотношение является прямым следствием линейности преобразования Фурье.

Масштабируемость

\[ \begin{matrix} \dfrac{1}{a} f\left( \dfrac{t}{a} \right) \supset F(pa) \\ f(ta) \supset \dfrac{1}{a} F\left( \dfrac{p}{a} \right) \end{matrix} \quad \forall a>0. \]

Доказательство. Рассмотрим преобразование Лапласа функции $$f\left( \frac{t}{a} \right)$$: \[ \int\limits_0^{+\infty} f\left( \dfrac{t}{a} \right) e^{-pt} dt = \left\{ \begin{matrix} z = at \\ dz = adt \end{matrix} \right\} = \int\limits_0^{+\infty} f(z) e^{-paz} a\,dz = aF(pa). \]

Аналогично доказывается вторая формула. $$\blacksquare$$

Сдвиг №1

Запаздывающий сигнал.

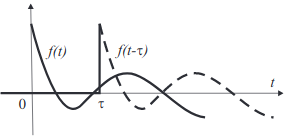
Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо: \[ \chi(t-\tau)f(t-\tau) \supset e^{-p\tau}F(p) \]

Доказательство. Применим преобразование Лапласа к функции $$\chi(t-\tau) f(t-\tau)$$. Сделав замену переменной $$\xi = t-a$$, получим \[ \int\limits_\tau^{+\infty} f(t-\tau) e^{-pt} dt = \int_0^{+\infty} f(\xi) e^{-p(\tau+\xi)} d\xi = e^{-p\tau} F(\xi) \quad \blacksquare \]

Сдвиг №2

Оригинальный и сдвинутый сигналы.

Пусть $$\chi(t) f(t) \supset F(t)$$. Тогда $$\forall \tau>0$$ справедливо:

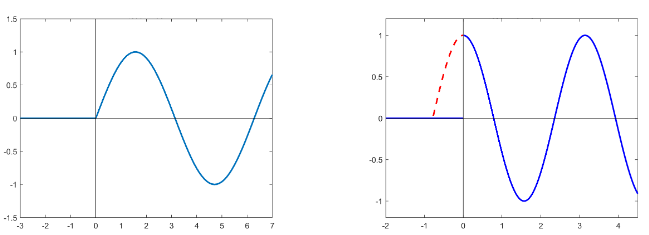
\[ \chi(t) f(t+a) \supset e^{pa} \left( F(p) - \int\limits_0^a f(\xi) e^{-p\xi} d\xi \right) \]

Доказательство. Найдём преобразование Лапласа для функции $$\chi(t) f(t+a)$$: \[ \int\limits_0^{+\infty} f(t+a)e^{-pt} dt = \int\limits_0^{+\infty} e^{-p(\xi-a)} d\xi - \int\limits_0^a f(\xi) e^{-p(\xi-a)} d\xi \quad \blacksquare \]

Заметим, что вычитаемое в этой формуле соответствует утерянной части сигнала.

Дифференцирование оригинала

Если функция $$f(t) \in C'(0, +\infty)$$ и она удовлетворяет достаточным условиям существования прямого преобразования Лапласа, тогда выполнено следующее соотношение: \begin{equation}\label{LT_Deriv} f'(t) \supset pF(p) -f(0+0). \begin{equation}

В общем случае: если $$f(t) \in C^{(k)}(0,+\infty)$$ и выполнены достаточные условия существования прямого преобразования, то \[ f^{(k)}(t) \supset p^k F(p) - p^{k-1} f(0+0) - p^{k-2} f'(0+0) - \dots - pf^{(k-2)}(0+0) - f^{(k-1)}(0+0). \]

Доказательство. Посчитаем преобразование Лапласа от функции $$f'(t)$$. Используя интегрирование по частям, получаем: \[ \int\limits_0^{+\infty} f'(t) e^{-pt} dt = f(t) e^{-pt} \bigg|_0^{+\infty} - \int\limits_0^{+\infty} f(t) (-p) e^{-pt} dt = 0 - f(0+0) + pF(p). \]

Далее найдём изображение второй производной, дважды применив формулу \eqref{LT_Deriv}: \[ f''(t) = \left( f(t) \right)' \supset p\left( pF(p) - f(0+0) \right) - f'(0+0) = p^2 F(p) - pf(0+0) - f'(0+0). \]

Далее, по методу математической индукции, находим: \[ f^{(k)} = \left( f^{(k-1)}(t) \right) \supset p \left( p^{k-1} F(p) -\sum\limits_{} \right) \]

Периодическая функция

Пусть $$f(t)$$ — периодическая функция с периодом $$T>0$$.

\[ \int\limits_0^{+\infty} f(t) e^{-pt} dt = \sum\limits_{k=1}^{+\infty} \int_{(k-1)T}^{kT} f(t) e^{-pt} dt = \left\{ t = (k-1)T + s \right\} = \sum\limits_{k=1}^{+\infty} \int_0^T f(s) e^{-ps} e^{-p(k-1)T} ds = \left( \sum\limits_{k=1}^{+\infty} e^{-p(k-1)T} \right) \int\limits_0^T f(s) e^{-ps} ds = \dfrac{1}{1-e^{-pT}} \int\limits_0^T f(s) e^{-ps} ds, \] то есть в случае периодической функции достаточно посчитать интеграл Лапласа на одном периоде.