Фазовый объём. Теорема Лиувилля

Определения

Определение 1.

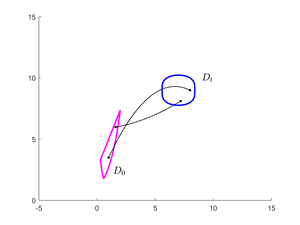
Пусть рассматривается система обыкновенных дифференциальных уравнений: \begin{gather*} \frac{dx_i}{dt}=f_i(x),\quad \text{где}\quad x\in \mathbb{R}^n\quad \text{и}\quad f\in \mathbb{R}^n;\\ x(0)=x_0\in D_0. \end{gather*} Введём обозначение для множества решений системы в фиксированный момент времени: \begin{gather*} D_t=\left\{\,x(\,t;x_0),\quad x_0\in D_0\right\}. \end{gather*} Фазовым объёмом множества $$D_t$$ называется выражение, определяемое по интегральной формуле: \begin{gather*} %V_t=\underbrace{\int...\int}_{D_t} dx_1\,dx_2...dx_n. V_t=\int\limits_{D_t} dx_1 dx_2...dx_n.\\ \end{gather*}
Определение 2.

Величина $$\dfrac{dv_t}{dt}$$ называется изменением фазового объёма.

Вспомогательные леммы

Лемма 1. (Уравнение в вариациях)

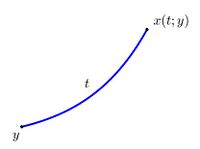
$$\quad$$ Пусть задана система обыкновенных дифференциальных уравнений: \begin{equation} \label{1} \frac{dx}{dt}=f(x),\quad \text{где}\quad x\in \mathbb{R}^n\quad \text{и}\quad f\in \mathbb{R}^n; \end{equation}

\begin{equation} x(0)=y, \quad y\in D_0. \end{equation}

Считаем, что $$x(t;y)-$$ решение системы (1-2) является дважды непрерывно дифференцируемой вектор-функцией в некоторой области, в которой и происходит рассмотрение леммы.

Запишем матрицу чувствительности начальных данных:

\begin{gather*} &\frac{\partial x(t;y)}{\partial y}=\bigg(\frac{\partial x_i}{\partial y_j}\bigg)_{i,j=\overline{1,n}}= \begin{pmatrix} \frac{\partial x_1}{\partial y_1}& \frac{\partial x_1}{\partial y_2}& ... & \frac{\partial x_1}{\partial y_n}\\ \frac{\partial x_2}{\partial y_1}& \frac{\partial x_2}{\partial y_2}& ... & \frac{\partial x_2}{\partial y_n}\\ ...&...&...&...\\ \frac{\partial x_n}{\partial y_1}& \frac{\partial x_n}{\partial y_2}& ... & \frac{\partial x_n}{\partial y_n}\\ \end{pmatrix}. \end{gather*} В этой матрице $$\dfrac{\partial x_i}{\partial y_j}-$$ скорость изменения координаты $$x_i$$ в зависимости от начального значения $$y_j.$$

Запишем ещё одну матрицу:

\begin{gather*} &\frac{\partial f}{\partial x}=\bigg(\frac{\partial f_i}{\partial x_j}\bigg)_{i,j=\overline{1,n}}= \begin{pmatrix} \frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& ... & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& ... & \frac{\partial f_2}{\partial x_n}\\ ...&...&...&...\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& ... & \frac{\partial f_n}{\partial x_n}\\ \end{pmatrix}. \end{gather*}

Тогда лемма утверждает, что справедливо матричное равенство (уравнение в вариациях): \begin{equation} \frac{d}{dt}\bigg(\frac{\partial x(t;y)}{\partial y}\bigg)=\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t;y)}{\partial y}\bigg). \end{equation} Доказательство.

\begin{gather*} (1)\Leftrightarrow \frac{dx_k(t;y)}{dt}=f_k\big(x(t;y)\big) \quad \bigg| \cdot \frac{\partial}{\partial y_j}\\ \frac{\partial}{\partial y_j}\frac{dx_k(t;y)}{dt}=\left\{\text{Переставим операции местами, в силу гладкости}\right\}=\frac{d}{dt}\frac{\partial x_k(t;y)}{\partial y_j}=\frac{\partial}{\partial y_j}\Big(f_k\big(x(t;y)\big)\Big)=\\ =\sum\limits_{s=1}^n \frac{\partial f_k}{\partial x_s} \cdot \frac{\partial x_s}{\partial y_j}=\bigg(\frac{\partial f_k}{\partial x_1},...,\frac{\partial f_k}{\partial x_n}\bigg)\cdot\bigg(\frac{\partial x_1}{\partial y_j},...,\frac{\partial x_n}{\partial y_j}\bigg)^T=\frac{\partial f_k}{\partial x}\cdot\bigg(\frac{\partial x(t;y)}{\partial y_j}\bigg). \end{gather*}

$$\blacksquare$$

Лемма 2. (Лиувилля, о дифференцировании определителя)

$$\quad$$ Пусть задана матрица $$A=\big(a_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}.$$

По определению след матрицы $$A$$ считается, как $$\,Tr A=\sum\limits_{i=1}^n a_{ii}.$$

Тогда справедливо следующее равенство: \begin{gather*} \frac{d}{dt}|A(t)|=|A(t)|\cdot Tr(A^{'}A^{-1}(t)), \text{ где } A^{'}(t)=\big(a^{'}_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}. \end{gather*}

Доказательство.

Необходимо быть знакомым с понятием $$\bar{o}$$-малое.

По формуле Тейлора имеем: \begin{gather*} a_{ij}(t+\Delta t)=a_{ij}(t)+a^{'}_{ij}(t)\Delta t+\bar{o}(\Delta t).\\ |A(t+\Delta t)|=|A(t)+A^{'}(t)\Delta t+\bar{o}(\Delta t)|=\bigg|\big(E+A^{'}(t)A^{-1}(t)\Delta t+\bar{o}(\Delta t)\big)A(t)\bigg|=\\ =\big|A(t)\big|\cdot\big|E+A^{'}(t)A^{-1}(t)\Delta t+\bar{o}(\Delta t)\big|. \end{gather*}

\begin{gather*} \big|E+\underbrace{A^{'}(t)A^{-1}(t)}_{b_{ij}}\Delta t+\bar{o}(\Delta t)\big|= \begin{vmatrix} 1+b_{11}\Delta t& b_{12}\Delta t& ... & b_{1n}\Delta t\\ b_{21}\Delta t& 1+b_{22}\Delta t& ... & b_{2n}\Delta t\\ ...&...&...&...\\ b_{n1}\Delta t& b_{n2}\Delta t& ... & 1+b_{nn}\Delta t\\ \end{vmatrix}+\bar{o}(\Delta t) =1+\Delta t\cdot Tr(A^{'}A^{-1})+\bar{o}(\Delta t). \end{gather*}

\begin{gather*} \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=\frac{\big|A(t)\big|\cdot \big(1+\Delta t \cdot Tr(A^{'}A^{-1})+\bar{o}(\Delta t)-1\big)}{\Delta t}=|A(t)|\cdot \big(Tr(A^{'}A^{-1}(t))+\bar{o}(1)\big)\\ \lim\limits_{\Delta t\to 0} \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=\frac{d}{dt}|A(t)|=|A(t)|\cdot Tr(A^{'}A^{-1}(t)). \end{gather*}

$$\blacksquare$$

Теорема Лиувилля об изменении фазового объёма

Теорема.

$$\quad$$ Пусть задана система обыкновенных дифференциальных уравнений: \begin{gather*} \frac{dx}{dt}=f(x),\quad \text{где}\quad x\in \mathbb{R}^n\quad \text{и}\quad f\in \mathbb{R}^n;\\ x(0)=y, \quad y\in D_0. \end{gather*} Также заданы множества решений системы в фиксированные моменты времени: \begin{gather*} D_t=\left\{\,x(\,t;y),\quad y\in D_0\right\}.\\ |D_0|=V_0, \quad |D_t|=V_t. \end{gather*} Тогда верна следующая формула для нахождения изменения фазового объёма: \begin{gather*} \frac{d V_t}{dt}=\int\limits_{D_t} div\, f\, dx_t,\quad \text{ где }\quad d x_t=dx_1\,dx_2\,...\,dx_n. \end{gather*} Напомним определение дивиргенции векторного поля $$f:$$ \begin{gather*} div\, f=\sum\limits_{i=1}^n \frac{\partial f_i}{\partial x_i}(x). \end{gather*}

Доказательство.

Необходимо быть знакомым с понятием якобиан системы.

\begin{gather*} dx_t=dx_1(t;y)\,dx_2(t;y)\,...\, dx_n(t;y)=\bigg|\frac{\partial x(t;y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n \quad \Rightarrow \\ \Rightarrow \quad V_t=\int\limits_{D_t} dx_t=\int\limits_{D_t} dx_1(t;y)\,dx_2(t;y)\,...\, dx_n(t;y)=\int\limits_{D_0} \bigg|\frac{\partial x(t;y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n.\\ \end{gather*}

\begin{gather*} \frac{dV_t}{dt}=\int\limits_{D_0} \frac{d}{dt}\bigg(\bigg|\frac{\partial x(t;y)}{\partial y}\bigg|\bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 2}\right\}=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t;y)}{\partial y}\bigg|\cdot Tr\Bigg(\frac{d}{dt}\bigg(\frac{\partial x(t;y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t;y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 1}\right\}=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t;y)}{\partial y}\bigg|\cdot Tr\Bigg(\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t;y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t;y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t;y)}{\partial \vec{y}}\bigg|\cdot Tr\bigg(\frac{\partial \vec{f}}{\partial x}\bigg) \,dy_1\,dy_2\,...\, dy_n=\int\limits_{D_t} Tr\bigg(\frac{\partial f}{\partial x}\bigg) dx_t=\int\limits_{D_t} div\, f\, dx_t. \end{gather*}

$$\blacksquare$$

Следствие теоремы Лиувилля для линейных систем

Следствие.

Пусть задана система линейных дифференциальных уравнений: \begin{gather*} \frac{dx_i}{dt}=\sum\limits_{j=1}^n a_{ij}\,x_j. \end{gather*} Её также можно записать в матричном виде: \begin{gather*} \dot{x}=Ax=f(x), \quad { где } \quad A=\big(a_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}. \end{gather*} Очевидно, что при таких условиях верно: \begin{gather*} div\,f=Tr(A). \end{gather*}

Тогда по Теореме Лиувилля имеем: \begin{gather*} \frac{d V_t}{dt}=\int\limits_{D_t} Tr(A) dx_t=Tr(A)\int\limits_{D_t} dx_t=Tr(A)\cdot V_t. \end{gather*} Таким образом, получили дифференциальное уравнение, решение которого элементарно находится: \begin{gather*} V_t=V_0\, e^{Tr(A)t}. \end{gather*} Понятно, что с использованием свойств экспоненты можно заключить следующее:

• $$\quad Tr(A)>0 \quad \Rightarrow \quad \text{траектории разбегаются.}$$
• $$\quad Tr(A)<0 \quad \Rightarrow \quad \text{траектории сближаются.}$$
• $$\quad Tr(A)=0 \quad \Rightarrow \quad \text{фазовый объём сохраняется.}$$

Пример сохранения фазового объёма

Пример.

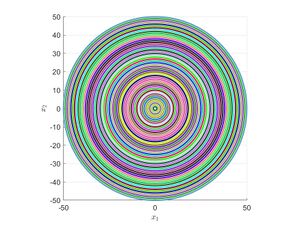
Пусть задана линейная система ОДУ:

\begin{gather*} \begin{cases} \dot{x}_1=x_2,\\ \dot{x}_2=-x_1. \end{cases} \end{gather*} Тогда матрица $$A$$ системы выписывается элементарно: \begin{gather*} A=\begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}. \end{gather*} \begin{gather*} Tr(A)=0,\text{ то есть фазовый объём сохраняется.} \end{gather*}

Фазовое пространство системы из примера. Траектории являются замкнутыми кривыми.

Показать сохранение фазового объёма можно и через первый интеграл (или энергию системы): \begin{gather*} \frac{dx_2}{dx_1}=-\frac{x_1}{x_2},\\ \int x_2 \, dx_2=-\int x_1 \, dx_1,\\ x_1^2+x_2^2=Const,\\ H(x_1,x_2)=x_1^2+x_2^2 \quad \text{- энергия системы.} \end{gather*} Итак, если $$(x_1(t),x_2(t))$$ - решение системы, то функция $$H(x_1(t),x_2(t))$$ не зависит от $$t:$$ \begin{gather*} \frac{d}{dt} H(x_1(t),x_2(t))=\frac{\partial H(x_1(t),x_2(t))}{\partial x_1}\cdot \frac{dx_1}{dt}+\frac{\partial H(x_1(t),x_2(t))}{\partial x_2}\cdot \frac{dx_2}{dt}=2x_1x_2+2x_2(-x_1)=0. \end{gather*} Фазовые кривые являются окружностями, поэтому фазовый объём сохраняется.

Список литературы

1. Федорюк М. В. "Обыкновенные дифференциальные уравнения", М.: Наука, 1985.
2. Братусь А.С., Новожилов A.C., Платонов А.П. "Динамические системы и модели биологии", М.: ФИЗМАТЛИТ, 2010.
3. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.