Неподвижные точки системы

Динамические системы с дискретным временем

Пусть задана динамическая система с дискретным временем

\begin{equation} \label{sist1} N_{t+1}=f(N_{t}), N_{t}\in\mathbb{R}, f:\mathbb{R} \rightarrow \mathbb{R} \end{equation}

Определение 1.

Решения задачи (\ref{sist1}), не изменяющиеся с течением времени $$t$$ называются неподвижными точками отображения (\ref{sist1}). Неподвижные точки определяются как решение уравнения $$N=f(N)$$.

Заметим, что нередко функцию $$f(N)$$ представляют в виде $$f(N)=Nf(N)$$, чтобы подчеркнуть существование тривиальной неподвижной точки $$N^{*}=0$$. В этом случае остальные неподвижные точки — решения уравнения $$f(N)$$

Устойчивость неподвижных точек

$$r=30, b=3$$, система имеет два различных неотрицательных корня.

$$r=0.9, b=7$$, система имеет единственный корень $$v=0$$.

Определение 2.

Неподвижная точка $$N^{*}$$ отображения (\ref{sist1}) называется устойчивой по Ляпунову, если для любого $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что для любых начальных данных $$N_{0}$$ из $$\delta$$-окрестности точки $$N^{*}$$ вся траектория системы $$N_{t}$$, $$t = 0, 1, 2, ...$$ содержится в $$\varepsilon$$-окрестности точки $$N^{*}$$.

Если, кроме того, $$\displaystyle{\lim_{t\to\infty}} N_{t} = N^{*}$$, то точка $$N^{*}$$ называется асимптотически устойчивой.

Асимптотически устойчивые неподвижные точки иногда называют аттракторами, а неустойчивые неподвижные точки иногда называют репеллерами.

Теорема 1.

Пусть $$N^{*}$$ — неподвижная точка отображения (\ref{sist1}), т.е. $$N^{*}$$ = $$f(N^{*})$$, и пусть $$f$$ обратима в малой окрестности $$N^{*}$$. Тогда $$N^{*}$$ асимптотически устойчива, если $$|f^{'}(N^{*})| < 1$$, и неустойчива, если $$|f^{'}(N^{*})| > 1$$. Если $$ |f^{'}(N^{*})| = 1$$, то требуются дополнительные исследования.

Доказательство.

Пусть $$|f^{'}(N^{*})| < 1$$ и пусть $$N$$ принадлежит малой окрестности $$N^{*}$$. Так как \[ \displaystyle{\lim_{t\to\infty}} \frac{|f(N)-f(N^{*})|}{|N-N^{*}|}=|f^{'}(N^{*})|, \] поэтому существует такая окрестность $$N^{*}$$, что \[ \frac{|f(N)-f(N^{*})|}{|N-N^{*}|} \leqslant a, \] для всех $$N$$ из этой окрестности; здесь $$a$$ — некоторое число, такое что $$|f^{'}(N^{*})| \leqslant a < 1$$. Таким образом, $$f(N)$$ остается в той же окрестности, что и $$N$$, и, кроме того, ближе к неподвижной точке $$N^{*}$$, по крайней мере, на множитель $$a$$. Отсюда следует, что \[|f(f(N)) − f(f(N^{*}))| \leqslant a |f(N) − f(N^{*})| \leqslant a^2|N − N^{*}|, \] или, по индукции, \[|f^{k}(N) − N^{*}| \leqslant a^{k}|N − N^{*}|, \] где $$f^{k}$$ обозначает $$k$$-ую суперпозицию отображения $$f$$. Таким образом мы доказали,что последовательность $$f^{k}(N)$$ будет сходиться к $$N^{*}$$, то есть является асимптотически устойчивой.

Вторая часть утверждения доказывается сходным образом. $$\blacksquare$$

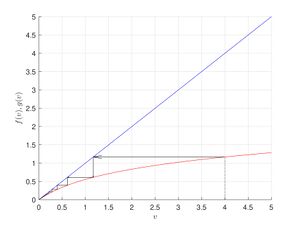
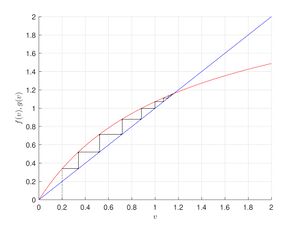
Пример поиска неподвижных точек с помощью графического метода

Аттрактор в точке $$v_2^*$$ при параметрах $$r=10, b=2, v_0=1.$$

Аттрактор в точке $$v_2^*$$ при параметрах $$r=3, b=0.9, v_0=4.5$$.

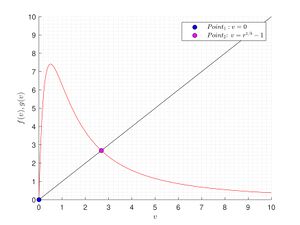
Пусть задана система $$v_{t+1} = \frac{r v_t}{(1+ v_t)^b}$$.

Графически неподвижные точки — это точки пересечения графика функции $$f(N)$$ и биссектрисы первого координатного угла $$N_{t+1} = N_{t}$$ (нас интересуют только неотрицательные решения). Для нахождения неподвижных точек заданной системы рассмотрим возможные пересечения графика функции $$f(v)=\frac{rv}{(1+v)^b}$$ с прямой $$g(v)=v$$.

Заметим, что система \begin{equation} \label{sist2} \begin{cases} f(v)=\frac{rv}{(1+v)^b},\\g(v)=v. \end{cases} \end{equation} при любых $$v \geqslant 0, ~r,b > 0$$ имеет хотя бы один корень, а именно $$v=0$$. Второй корень $$v=r^{1/b}-1$$ система может иметь только при значении параметра $$r> 1$$. Больше двух неотрицательных корней система (\ref{sist2}) не имеет.

Аттрактор в точке $$v_1^*$$ при параметрах $$r=0.9, b=0.7, v_0=4.$$

Репеллер в точке $$v_1^*$$ при параметрах $$r=2, b=0.9, v_0=2.$$

Пример исследования неподвижных точек на устойчивость для системы с дискретным временем

Исследуем на устойчивость неподвижные точки $$v^{*}_1=0$$ и $$v^{*}_2=r^{1/b}-1$$ для системы (\ref{sist2}).

\begin{equation} f_v(v^{*})=\frac{r((1+v)^b-bv(1+v)^{b-1})}{(1+v)^{2b}}. \end{equation}

Исследуем сначала точку $$v^{*}_2=r^{1/b}-1$$:

Подставим $$v_2^{*}$$ в выражение (\ref{sist2}) и с учетом наложенных ограничений $$r>1, b>0$$ для существования точки получим

\[ f_v(v_2^{*})=b(r^{-1/b}-1)+1. \]

Согласно теореме 1 точка $$v^{*}_2=r^{1/b}-1$$ будет асимптотически устойчивой, при $$r^{-1/b}<1$$ и неустойчивой при $$r^{-1/b}>1$$. Отметим, что точка $$v^{*}_2=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, точка $$v^{*}_2$$ асимптотически устойчива всегда, если она существует.

Теперь исследуем на устойчивость точку $$v^{*}_1=0$$:

Подставим $$v_1^{*}$$ в выражение (\ref{sist2}) и получим \[ f_v(v_1^{*})=r. \] Таким образом, по теореме 1, точка $$v^{*}_1=0$$ будет асимптотически устойчивой, при $$r<1$$ и неустойчивой при $$r>1$$.

Динамические системы с непрерывным временем

Определение 3.

Точка $$a \in \mathbb{R}^n$$ называется неподвижной точкой динамической системы $$\dot x_i = f_i(x_1,...,x_n)$$, где $$(x_1,...,x_2) \in D \subset \mathbb{R}^n, i=\overline{1,n}, f=(f_1,...,f_n)$$, если $$f(a)=0$$.

Пусть задана динамическая система с непрерывным временем

\begin{equation} \label{sist3} \dot u=f(u), u \in U \subseteq \mathbb{R}^{n}, f: U \rightarrow \mathbb{R}^{n}. \end{equation}

Определение 4.

Положение равновесия динамической системы (\ref{sist3}) называется гиперболическим, если число собственных значений $$n_0$$ якобиана вектор-функции $$f(u)$$ равняется нулю, т.е. не существует собственных чисел, расположенных на мнимой оси матрицы Якоби. Гиперболическое положение равновесия называется гиперболическим седлом, если $$n_+$$ $$n_- \neq 0$$, где $$n_+$$, $$n_-$$, $$n_0$$ — количество собственных значений якобиана (с учётом их кратности) с положительной, отрицательной и равной нулю вещественной частью соответственно.

Теорема 2 (А. М. Ляпунов, А. Пуанкаре).

Пусть $$u^*$$ — гиперболическое положение равновесия (\ref{sist3}). Тогда, если $$n_+=0$$, то положение равновесия $$u^*$$ асимптотически устойчиво, если $$n_+>0$$, то неустойчиво.

Устойчивость гиперболического положения равновесия определяется собственными числами матрицы Якоби, вычисленными в точке $$u^*$$. В случае, когда вещественная часть одного или нескольких собственных значений равна нулю, необходимы дополнительные исследования.

Пример поиска неподвижных точек для системы с непрерывным временем и исследования на устойчивость

Рассмотрим динамическую систему

\begin{equation} \label{sist4} \begin{cases} uv=\dfrac{\mu \nu u^2}{1+u},\\ uv=v \mu. \end{cases} \end{equation}

Из второго уравнения системы (\ref{sist4}):

Пусть $$v=0$$. Тогда $$\dfrac{\mu \nu u^2}{1+u}=0, \mu,\nu>0$$, значит $$u=0$$.

Пусть $$v \neq 0$$. Тогда $$u = \mu$$ и $$v = \dfrac{\mu^2 \nu}{1+\mu}$$.

Других решений система (\ref{sist4}) не имеет.

Получили 2 неподвижные точки:

1) $$u=0,v=0$$. Обозначим как точку $$A$$.

2) $$u=\mu, v=\frac{\mu^2 \nu}{1+\mu}$$. Обозначим как точку $$B$$.

Чтобы исследовать найденные неподвижные точки на устойчивость, выпишем якобиан системы (\ref{sist4}) и воспользуемся теоремой 2.

\begin{equation} \label{jacobian} J(u,v) = \begin{bmatrix} \frac{2 \mu \nu u}{1+u} - \frac{\mu \nu u^2}{(1+u)^2} - v & -u \\ v & u-\mu \end{bmatrix} \end{equation}

Рассмотрим значения якобиана в точкe $$A=(0,0)$$.

\begin{equation} J(A) = \begin{bmatrix} 0 & 0 \\ 0 & -\mu \end{bmatrix}\ \end{equation}

Собственными значениями являются числа $$\lambda_1=0, \lambda_2=-\mu$$. В этом случае теорема 2 не применима. Устойчивость точки $$A=(0,0)$$ без дополнительных исследований установить нельзя.

Рассмотрим значения якобиана в точкe $$B=\left(\mu,\frac{\mu^2 \nu}{1+\mu}\right)$$.

\begin{equation} J(B) = \begin{bmatrix} \frac{\mu^2 \nu}{\mu+1}-\frac{\mu^3 \nu}{(\mu+1)^2} & - \mu \\ \frac{\mu^2 \nu}{\mu+1} & 0 \end{bmatrix}\ \end{equation}

Найдём собcтвeнные значения.

\[ \det(J(B)- I \cdot \lambda) = \begin{bmatrix} \frac{\mu^2 \nu}{\mu+1}-\frac{\mu^3 \nu}{(\mu + 1 )^2} - \lambda & - \mu \\ \frac{\mu^2 \nu}{\mu+1} & - \lambda \end{bmatrix}\ = - \lambda \left( \frac{\mu^2 \nu}{\mu+1} - \frac{\mu^3 \nu}{(\mu+1)^2 } - \lambda \right) + \frac{\mu^3 \nu}{\mu+1} =0. \]

\[ (\mu+1)^2 \lambda^2 - \mu^2 \nu \lambda + (\mu + 1) \mu^3 \nu =0. \]

Далее решаем квадратное уравнение относительно $$\lambda$$. Дискриминант: \[ D = (\mu^2 \nu)^2 - 4(\mu + 1)^2(\mu+1) \mu^3 \nu = \mu^4 \nu^2 - 4\mu^3 \nu (\mu^3 + 3\mu^2 + 3\mu +1). \]

Тогда корни уравнения: \[ \lambda_{1,2} = \frac{\mu^2 \nu \pm \sqrt{\mu^4 \nu^2 - 4 \mu^3 \nu (\mu^3 + 3\mu^2 + 3\mu +1)}}{2(\mu+1)^2} \]

Так как параметры $$\mu, \nu>0$$, то положения равновесия являются гиперболическими. Возможны 2 случая:

1) $$D \geqslant 0$$.

Этот случай возникает при $$\nu \geqslant 4(\mu^2 + 3\mu + 3 + \frac{1}{\mu})$$. Собственные значения $$\lambda_{1,2}$$ будут вещественными и положительными, таким образом положение равновесия — узел.

По теореме 2 узел будет неустойчивым.

2) $$D < 0$$.

Этот случай возникает при $$\nu < 4(\mu^2 + 3\mu + 3 + \frac{1}{\mu})$$. Собственные значения $$\lambda_{1,2}$$ будут комплексными с положительной вещественной частью, значит положение равновесия — фокус.

По теореме 2 фокус будет неустойчивым.

Приведем параметрический портрет системы.

В области $$I$$ точка $$B$$ будет неустойчивым узлом. В области $$II$$ точка $$B$$ будет неустойчивым фокусом.

Список литературы

1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.

2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.