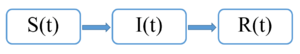Математическая модель распространения эпидемий

Математические модели эпидемиологии — динамические системы, описывающие распространение инфекционных популяций среди здоровых.

Не все заболевания рассматриваются в рамках такого исследования: моделируются инфекции, вызываемые микропаразитами. В таком случае можно пренебречь динамикой каждого паразита (в отличие от случая макропаразитов), поскольку заболевание протекает у инфицированных с одинаковым характером. Поэтому обладания информацией о динамике здоровой популяции и заражённой достаточно для анализа модели.

Общая формулировка SIR-модели

Одна из простейших моделей распространения эпидемий — SIR-модель. Это модель ящикового вида, в которой все особи популяции разделяются на группы — "ящики", — внутри которых особи неразличимы.

Диаграмма эволюции особи популяции в SIR-модели

В SIR-модели все особи поделены на 3 группы:

1. \(S(t)\) — подверженные заболеванию особи (от англ. susceptible)
2. \(I(t)\) — заражённые особи (от англ. infected)
3. \(R(t)\) — переболевшие (от англ. resistant)

Важно отметить, что ящиковая модель, в том числе и SIR-модель, подразумевает собой замкнутую популяцию, в которой не происходят процессы рождаемости и смертности. Поэтому на введённые классы можно выписать ограничение\[ S + I + R = N, \] где \( N \) — общее число особей популяции.

Замечание. Из замкнутости популяции и характера эволюции особи можно сделать вывод, что с течением времени "ящик" \(I\) заражённых особей станет пустым.

Исследование SIR-модели

Функция инфективности

Для анализа сформулированной модели вводится функция инфективности \(A(\tau)\), которая характеризует вероятность того, что произойдёт заражение индивида при контакте с заражённым индивидом \(\tau\) единиц времени назад.

В общем виде функция инфективности выглядит следующим образом:\[ A(\tau) = \begin{equation} \begin{cases} c \cdot p,\ \ t \in [T_1,\ T_2]\\ 0,\ \ \text{иначе}. \end{cases} \label{sys1} \end{equation} \]

Здесь \(p\) — вероятность заражения, а \(c\) — среднее число контактов в единицу времени. Промежуток времени \(t \in [T_1,\ T_2]\) — окно, в течение которого индивидуум заразен.

Таким образом, в частном случае \(A(\tau)\) можно ввести так:\[ A(\tau) = \underbrace{\beta N}_{c} \cdot \underbrace{\exp\{ -\gamma\tau \} }_{p},\ \ \beta=const,\] то есть, заражение распределено экспоненциально со средним \(\frac{1}{\gamma}\). Следовательно, средняя длина промежутка времени, в течение которого индивид заразен, равна \(\frac{1}{\gamma}\).

Замечание. Введя подобным образом функцию инфективности, получают, что число контактов растёт линейно с общим объёмом популяции \(N\), что, вообще говоря, является довольно грубым допущением. Однако оно необходимо для упрощения и наглядности исследования.

Получение аналитического вида SIR-модели

Рассмотрим ещё одну величину \(i(t)\) — число новых заболевших в момент времени \(t\). Таким образом, \(i(t) = -\dot{S}(t)\).