Динамическая система: различия между версиями
| (не показано 28 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
| − | '''Динамическая система''' | + | '''Динамическая система''' — это абстрактная математическая модель, которая состоит из множества элементов, связанных между собой функциональной зависимостью между временем и положением в фазовом пространстве каждого элемента системы. Такая модель позволяет изучать и описывать эволюцию системы во времени. |
| − | Определение динамической системы является математической формализацией общей научной концепции [https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C детерминированного процесса]. Процесс называется детерминированным, если | + | Определение динамической системы является математической формализацией общей научной концепции [https://ru.wikipedia.org/wiki/%D0%94%D0%B5%D1%82%D0%B5%D1%80%D0%BC%D0%B8%D0%BD%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C детерминированного процесса]. Процесс называется детерминированным, если все его будущее и прошлое |
| − | однозначно | + | однозначно определяется состоянием в настоящее время. |
==Введение== | ==Введение== | ||
| − | ''Динамическая система'' может быть представлена как система, которая имеет '' | + | $$\quad$$ ''Динамическая система'' может быть представлена как система, которая имеет ''состояния''. Подход, основанный на состоянии, позволяет описать динамику процесса. [https://sawiki.cs.msu.ru/index.php?title=%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D1%8B%D0%B5_%D0%B8_%D0%B8%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BA%D1%80%D0%B8%D0%B2%D1%8B%D0%B5._%D0%A4%D0%B0%D0%B7%D0%BE%D0%B2%D0%BE%D0%B5_%D0%BF%D1%80%D0%BE%D1%81%D1%82%D1%80%D0%B0%D0%BD%D1%81%D1%82%D0%B2%D0%BE&action=edit&redlink=1 Фазовое пространство] системы представляет собой набор ''всех допустимых состояний'' динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, определяющим переход системы из начального состояния в другое. |
| − | Основная задача теории динамических систем | + | $$\quad$$ Основная задача теории динамических систем — это исследование поведения систем. Это включает разбиение фазового пространства на траектории и изучение предельного поведения этих траекторий, таких как поиск и классификация положений равновесия, выделение притягивающих ([https://ru.wikipedia.org/wiki/%D0%90%D1%82%D1%82%D1%80%D0%B0%D0%BA%D1%82%D0%BE%D1%80 аттракторы]) и отталкивающих (''репеллеры'') множеств. Важнейшими понятиями теории динамических систем являются ''устойчивость состояний равновесия'' (способность системы при малых изменениях начальных условий оставаться около [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B положения равновесия] или на заданном множестве) и грубость (сохранение свойств при малых изменениях самой математической модели). Основные методы изучения динамических систем включают численное и аналитическое решение дифференциальных уравнений, а также геометрические методы анализа фазовых портретов. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Эволюционный оператор== | ==Эволюционный оператор== | ||
| Строка 70: | Строка 40: | ||
$$\quad$$Самый простой способ задать динамическую систему — указать эволюционный оператор в явном виде. Например, можно положить $$ϕ^1 = f(N) = 2N$$. То есть, за | $$\quad$$Самый простой способ задать динамическую систему — указать эволюционный оператор в явном виде. Например, можно положить $$ϕ^1 = f(N) = 2N$$. То есть, за | ||
| − | каждую единицу времени численность популяции увеличивается в 2 раза. | + | каждую единицу времени численность [https://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%BF%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F популяции] увеличивается в 2 раза. |
$$\quad$$Другой общий способ задания динамической системы — описать закон эволюции с помощью дифференциальных уравнений. | $$\quad$$Другой общий способ задания динамической системы — описать закон эволюции с помощью дифференциальных уравнений. | ||
| Строка 88: | Строка 58: | ||
\end{cases} | \end{cases} | ||
\end{equation*} | \end{equation*} | ||
| + | ==Примеры== | ||
| + | '''Пример 1'''. | ||
| + | |||
| + | $$\quad$$ Рассмотрим изолированную популяцию, находящуюся в неизменных условиях, не подвергающуюся | ||
| + | внешнему воздействию, каждая особь которой имеет одинаковый доступ к ресурсам, а так же, одинаковую вероятность встретить (и | ||
| + | таким образом конкурировать) другую особь популяции. | ||
| + | |||
| + | $$\quad$$ Так как численность не может быть отрицательной, то пространство состояний | ||
| + | в данном примере $$X = \mathbb{R}^+$$, где $$\mathbb{R}^+ = \{N ∈ \mathbb{R}: N > 0\}$$. Здесь следует отметить, | ||
| + | что если рассматривать численность как функцию времени, то очевидно, что эта | ||
| + | функция целочисленна, т.е. $$N(t) ∈ {N ∈ Z: N > 0}$$. Величина $$\dfrac{N(t + ∆t) − N(t)}{∆t}$$ | ||
| + | описывает среднюю скорость роста в интервале времени $$(t, t+∆t]$$. Если численность | ||
| + | популяции велика, то скачки, вызванные рождением и смертью отдельных индивидуумов, выглядят пренебрежимо малыми на графике функции $$N(t)$$. Поэтому можно рассмотреть следующую производную: \[\dfrac{dN(t)}{dt} = \lim\limits_{∆t→0}\dfrac{N(t + ∆t) − N(t)}{∆t} ≡ \dot{N}.\] | ||
| + | |||
| + | |||
| + | '''Пример 2: модель Мальтуса'''. [[Файл:Мальтус4.png|мини|Пример 2. Рост популяции и линейное распределение ресурсов]] | ||
| + | |||
| + | $$\quad$$''Модель Мальтуса'' — это экспоненциальный рост с постоянным темпом. Модель названа в честь английского демографа и экономиста [https://www.bing.com/ck/a?!&&p=fe40d8720325643eJmltdHM9MTcwMTgyMDgwMCZpZ3VpZD0xMWUxY2NjOS0xNjEyLTZjNWUtMzM5NC1jMzI1MTczYTZkNmImaW5zaWQ9NTE2Mw&ptn=3&ver=2&hsh=3&fclid=11e1ccc9-1612-6c5e-3394-c325173a6d6b&psq=%d0%a2%d0%be%d0%bc%d0%b0%d1%81%d0%b0+%d0%9c%d0%b0%d0%bb%d1%8c%d1%82%d1%83%d1%81%d0%b0.&u=a1aHR0cHM6Ly9ydS53aWtpcGVkaWEub3JnL3dpa2kvJUQwJTlDJUQwJUIwJUQwJUJCJUQxJThDJUQxJTgyJUQxJTgzJUQxJTgxLF8lRDAlQTIlRDAlQkUlRDAlQkMlRDAlQjAlRDElODFfJUQwJUEwJUQwJUJFJUQwJUIxJUQwJUI1JUQxJTgwJUQxJTgy&ntb=1 Томаса Мальтуса]. | ||
| + | |||
| + | $$\quad$$Мальтузианские модели выглядят следующим образом: | ||
| + | $$ N(t) = N_0e^{rt}$$, | ||
| + | где | ||
| + | |||
| + | * $$N_0 = N(0)$$ — исходная численность населения, | ||
| + | * $$r>0$$ — темп прироста населения («мальтузианский параметр»), | ||
| + | * $$t$$ — время. | ||
| + | |||
| + | $$\quad$$В дискретном времени эту же модель можно записать в виде: | ||
| + | $$N_{t+1} = mN_t$$, где $$m>0$$ — константа пропорциональности. Можно заметить, что если непрерывная и дискретная модель описывают одну и ту же популяцию, то $$r = \ln(m)$$. | ||
| + | |||
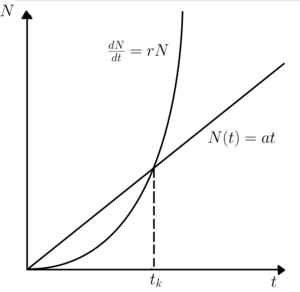
| + | $$\quad$$Заметим, что при линейном распределении ресурсов ($$N(t) = at$$, где $$N$$ — число особей, которым хватает ресурсов, а $$a$$ — темп прироста ресурсов), в модели Мальтуса существует точка кризиса ресурсов $$t_k$$, когда их перестает хватать на популяцию, поэтому существует множество усовершенствованных моделей учитывающих этот фактор. Например, можно сделать коэффициенты $$r, m$$ зависимыми от времени или использовать модель с [https://sawiki.cs.msu.ru//index.php/%D0%9B%D0%BE%D0%B3%D0%B8%D1%81%D1%82%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B8_%D0%B5%D0%B3%D0%BE_%D1%81%D0%B2%D0%BE%D0%B9%D1%81%D1%82%D0%B2%D0%B0 логистическим уравнением]. | ||
| − | + | '''Пример 3: Задача о росте числа кроликов'''[[Файл:Поколения2.png|мини|Пример 3. Поколения кроликов]] | |
| − | $$\quad$$ | + | $$\quad$$Одной из старейших и известнейших задач популяционной динамики является задача о росте числа кроликов. В этой задаче предполагается, что каждая пара кроликов через месяц после своего рождения производит другую пару кроликов, и рождение кроликов начинается со второго месяца. Эта задача была опубликована в 1202 году в "Трактате о счете" итальянского математика |
| + | [https://ru.wikipedia.org/wiki/%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8 Леонардо Пизанского], более известного как Фибоначчи. Решением этой задачи является знаменитая последовательность [https://ru.wikipedia.org/wiki/%D0%A7%D0%B8%D1%81%D0%BB%D0%B0_%D0%A4%D0%B8%D0%B1%D0%BE%D0%BD%D0%B0%D1%87%D1%87%D0%B8 чисел Фибоначчи]. Математическая формулировка этой задачи выглядит следующим образом: | ||
| − | + | \[ N_{t+1} = N_t + N_{t-1}, \] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | == | + | где $$N_t$$ — число пар кроликов в t-ый месяц, $$N_0 = 0,\ N_1 = 1$$. |
| − | + | $$\quad$$Т. е. динамическая система может выглядеть следующим образом: | |
| − | * | + | \begin{equation*} |
| − | + | \begin{cases} | |
| − | + | M_{t+1} = N_t,\\ | |
| − | * | + | N_{t+1} = N_t+M_t. |
| + | \end{cases} | ||
| + | \end{equation*} | ||
==Список литературы== | ==Список литературы== | ||
Текущая версия на 15:40, 11 декабря 2023
Динамическая система — это абстрактная математическая модель, которая состоит из множества элементов, связанных между собой функциональной зависимостью между временем и положением в фазовом пространстве каждого элемента системы. Такая модель позволяет изучать и описывать эволюцию системы во времени.
Определение динамической системы является математической формализацией общей научной концепции детерминированного процесса. Процесс называется детерминированным, если все его будущее и прошлое однозначно определяется состоянием в настоящее время.
Содержание
Введение
$$\quad$$ Динамическая система может быть представлена как система, которая имеет состояния. Подход, основанный на состоянии, позволяет описать динамику процесса. Фазовое пространство системы представляет собой набор всех допустимых состояний динамической системы. Таким образом, динамическая система характеризуется своим начальным состоянием и законом, определяющим переход системы из начального состояния в другое.
$$\quad$$ Основная задача теории динамических систем — это исследование поведения систем. Это включает разбиение фазового пространства на траектории и изучение предельного поведения этих траекторий, таких как поиск и классификация положений равновесия, выделение притягивающих (аттракторы) и отталкивающих (репеллеры) множеств. Важнейшими понятиями теории динамических систем являются устойчивость состояний равновесия (способность системы при малых изменениях начальных условий оставаться около положения равновесия или на заданном множестве) и грубость (сохранение свойств при малых изменениях самой математической модели). Основные методы изучения динамических систем включают численное и аналитическое решение дифференциальных уравнений, а также геометрические методы анализа фазовых портретов.
Эволюционный оператор
Эволюция динамической системы означает изменение состояния системы со временем $$t ∈ T$$, где $$T$$ — упорядоченное множество.
$$\quad$$В математической биологии применяются два типа динамических систем: непрерывные с временем $$T = \mathbb{R}$$ и дискретные с целочисленным временем $$T = Z$$.
$$\quad$$Основным компонентом любой динамической системы является закон эволюции, который определяет состояние системы $$x_t$$ в момент времени $$t$$, при условии, что начальное состояние $$x_0$$ известно.
$$\quad$$Самый общий способ описать закон эволюции — задать отображение: \[ϕ^t: X → X,\] которое переводит начальное состояние в состояние системы в момент $$t$$: $$x_t = ϕ^t x_0$$.
$$\quad$$Отображение $$ϕ^t$$ часто называют эволюционным оператором динамической системы. Эволюционный оператор имеет два естественных свойства, которые отражают детерминированный характер поведения динамической системы: \begin{equation} \label{eq:0} ϕ^0 x = x,\ \forall x \in X,\\ \end{equation} \begin{equation} \label{eq:1} ϕ^{t+s} = ϕ^t◦ϕ^s\ \text{или}\ ϕ^{t+s}x = ϕ^t(ϕ^sx),\ \forall x \in X. \end{equation} $$\quad$$Другими словами, свойство \eqref{eq:0} означает, что динамическая система не изменяет своего состояния «спонтанно», а свойство \eqref{eq:1},что результат эволюции системы в течение $$t + s$$ единиц времени тот же самый, как если бы сначала зафиксировать изменение системы за $$s$$ единиц времени и затем получить состояние измененной системы еще через $$t$$ единиц времени.
Определение динамической системы
$$\quad$$Динамической системой называется пара $${X,\ ϕ^t}$$, где $$X$$ — пространство состояний, $$ϕ^t$$ — однопараметрическое семейство эволюционных операторов, удовлетворяющее свойствам \eqref{eq:0} и \eqref{eq:1}.
$$\quad$$Самый простой способ задать динамическую систему — указать эволюционный оператор в явном виде. Например, можно положить $$ϕ^1 = f(N) = 2N$$. То есть, за каждую единицу времени численность популяции увеличивается в 2 раза.
$$\quad$$Другой общий способ задания динамической системы — описать закон эволюции с помощью дифференциальных уравнений.
$$\quad$$Предположим, что пространство состояний динамической системы есть подмножество $$X = U ⊆ \mathbb{R}^n$$ с координатами $$u = (u_1, u_2, . . . , u_n)$$. Закон эволюции задается неявно, в терминах скоростей изменения координат: \[\dot{u} = f(u),\ u ∈ U ⊆ \mathbb{R}^n,\ f : U → \mathbb{R}^n,\] или, в покоординатной форме записи:
\begin{equation*} \begin{cases} \dot{u}_1 = f_1(u_1, u_2, . . . , u_n),\\ \dot{u}_2 = f_2(u_1, u_2, . . . , u_n),\\ ...\\ \dot{u}_n = f_n(u_1, u_2, . . . , u_n). \end{cases} \end{equation*}
Примеры
Пример 1.
$$\quad$$ Рассмотрим изолированную популяцию, находящуюся в неизменных условиях, не подвергающуюся внешнему воздействию, каждая особь которой имеет одинаковый доступ к ресурсам, а так же, одинаковую вероятность встретить (и таким образом конкурировать) другую особь популяции.
$$\quad$$ Так как численность не может быть отрицательной, то пространство состояний в данном примере $$X = \mathbb{R}^+$$, где $$\mathbb{R}^+ = \{N ∈ \mathbb{R}: N > 0\}$$. Здесь следует отметить, что если рассматривать численность как функцию времени, то очевидно, что эта функция целочисленна, т.е. $$N(t) ∈ {N ∈ Z: N > 0}$$. Величина $$\dfrac{N(t + ∆t) − N(t)}{∆t}$$ описывает среднюю скорость роста в интервале времени $$(t, t+∆t]$$. Если численность популяции велика, то скачки, вызванные рождением и смертью отдельных индивидуумов, выглядят пренебрежимо малыми на графике функции $$N(t)$$. Поэтому можно рассмотреть следующую производную: \[\dfrac{dN(t)}{dt} = \lim\limits_{∆t→0}\dfrac{N(t + ∆t) − N(t)}{∆t} ≡ \dot{N}.\]
Пример 2: модель Мальтуса.
$$\quad$$Модель Мальтуса — это экспоненциальный рост с постоянным темпом. Модель названа в честь английского демографа и экономиста Томаса Мальтуса.
$$\quad$$Мальтузианские модели выглядят следующим образом: $$ N(t) = N_0e^{rt}$$, где
- $$N_0 = N(0)$$ — исходная численность населения,
- $$r>0$$ — темп прироста населения («мальтузианский параметр»),
- $$t$$ — время.
$$\quad$$В дискретном времени эту же модель можно записать в виде: $$N_{t+1} = mN_t$$, где $$m>0$$ — константа пропорциональности. Можно заметить, что если непрерывная и дискретная модель описывают одну и ту же популяцию, то $$r = \ln(m)$$.
$$\quad$$Заметим, что при линейном распределении ресурсов ($$N(t) = at$$, где $$N$$ — число особей, которым хватает ресурсов, а $$a$$ — темп прироста ресурсов), в модели Мальтуса существует точка кризиса ресурсов $$t_k$$, когда их перестает хватать на популяцию, поэтому существует множество усовершенствованных моделей учитывающих этот фактор. Например, можно сделать коэффициенты $$r, m$$ зависимыми от времени или использовать модель с логистическим уравнением.
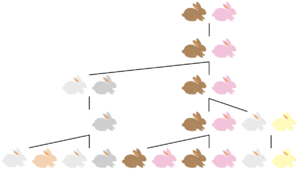
Пример 3: Задача о росте числа кроликов
$$\quad$$Одной из старейших и известнейших задач популяционной динамики является задача о росте числа кроликов. В этой задаче предполагается, что каждая пара кроликов через месяц после своего рождения производит другую пару кроликов, и рождение кроликов начинается со второго месяца. Эта задача была опубликована в 1202 году в "Трактате о счете" итальянского математика Леонардо Пизанского, более известного как Фибоначчи. Решением этой задачи является знаменитая последовательность чисел Фибоначчи. Математическая формулировка этой задачи выглядит следующим образом:
\[ N_{t+1} = N_t + N_{t-1}, \]
где $$N_t$$ — число пар кроликов в t-ый месяц, $$N_0 = 0,\ N_1 = 1$$.
$$\quad$$Т. е. динамическая система может выглядеть следующим образом: \begin{equation*} \begin{cases} M_{t+1} = N_t,\\ N_{t+1} = N_t+M_t. \end{cases} \end{equation*}
Список литературы
- Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
- Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.