Задача быстродействия "из точки в точку": различия между версиями
Tochilin (обсуждение | вклад) (Новая страница: «== Постановка задачи == ''Задача быстродействия'' - задача перевода системы из начального ф...») |
Alina22 (обсуждение | вклад) |
||
| (не показано 29 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
== Постановка задачи == | == Постановка задачи == | ||
| − | ''Задача быстродействия'' - задача перевода системы из начального фиксированного положения в конечное, также фиксированное, положение за минимальное время. | + | '''Задача быстродействия'''\(~-\) задача перевода системы из начального фиксированного положения в конечное, также фиксированное, положение за минимальное время. |
Пусть наша система описывается следующими условиями: | Пусть наша система описывается следующими условиями: | ||
\[ | \[ | ||
\begin{cases} | \begin{cases} | ||
| − | \dot{x}(t) = | + | \dot{x}(t) = f(x(t), u(t)), \\ |
x(t_0) = x^0, \\ | x(t_0) = x^0, \\ | ||
x(t_1) = x^1, \\ | x(t_1) = x^1, \\ | ||
| − | u(\tau) \in \mathcal{P}(\tau) \in \text{conv}\mathbb{R}^m, \\ | + | u(\tau) \in \mathcal{P}(\tau) \in \text{conv} \, \mathbb{R}^m, \\ |
| − | t_1 - t_0 \rightarrow \inf, | + | t_1 - t_0 \rightarrow \underset{u(\cdot)}{\text{inf}}, |
\end{cases} | \end{cases} | ||
\] | \] | ||
| − | где \( x_0, x_1, t_0 \) - фиксированы, \( A(t), B(t), f(t) \) - непрерывны, а \( \mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \( l: \rho(l\vert\mathcal{P}(\tau)\) по \(\tau\) непрерывна\(^1\)). | + | где \(x_0, x_1, t_0 \) \(~-\) фиксированы, \(A(t), B(t), f(t) \) \(~-\) непрерывны, а \(\mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \(l: \rho(l\vert\mathcal{P}(\tau)\) по \(\tau\) непрерывна\(^1\)). |
| − | \(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P} = [a(\tau), b(\tau)]\); | + | \(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P} = [a(\tau), b(\tau)]\); непрерывность многозначного отображения означает, что \(a(\tau), b(\tau)\) - непрерывны. |
| − | + | Заметим, что в общем случае функционал имеет вид: | |
| − | |||
| − | |||
| − | |||
\[ | \[ | ||
| − | \ | + | \mathcal{J} = \int\limits_{t_0}^{t_1}f^0(x(t), u(t))\,dt \rightarrow \underset{u(\cdot)}{\text{inf}} |
| − | |||
| − | |||
| − | |||
| − | |||
\] | \] | ||
| + | Принимая \(f^0 \equiv 1 \), получаем задачу быстродействия с функционалом \(\mathcal{J} = t_1 - t_0\). | ||
| − | + | '''Сопряженная переменная''' имеет следующий вид: \(\psi = (\psi_1, ..., \psi_n)\). | |
| − | + | Выпишем '''функцию Гамильтона-Понтрягина''': | |
| + | \[ | ||
| + | \mathcal{H}(\psi, x, u) = \langle \psi, f(x(t), u(t)) \rangle. | ||
| + | \] | ||
| − | + | Тогда можно говорить о сопряженной системе: | |
\[ | \[ | ||
| − | + | \dot{\psi} = -\frac{\partial \mathcal{H}}{\partial x(t)}. | |
\] | \] | ||
| − | + | Заметим, что '''гамильтонианом''' системы называется \(M = \underset{u\in \mathcal{P}}{\text{sup}} \, \mathcal{H}(\psi, x, u)\). Однако в задаче быстродействия супремум достижим, поэтому \(M = \underset{u\in \mathcal{P}}{\text{max}} \, \langle \psi, f(x(t), u(t)) \rangle\). | |
| − | + | == Принцип максимума Понтрягина == | |
| − | ==== | + | ==== Теорема(ПМП для автономной задачи быстродействия) ==== |
| − | + | Пусть \((x^*(\cdot), u^*(\cdot))\) \(~-\) оптимальная пара, \(\mathcal{H}\) \(~-\) функция Гамильтона–Понтрягина. Тогда существует \(\psi^*:[t_0, t_1] \rightarrow \mathbb{R}^n \), \(\psi^* \neq 0 \) такое, что: | |
| − | + | 1) Сопряженная система (СС): | |
| + | \[\dot{\psi} = -\frac{\partial H(\psi(t), x(t), u(t))}{\partial x(t)} \bigg|_{x=x^*(t) \\ u=u^*(t) \\ \psi = \psi^*(t)};\] | ||
| + | 2) Условие максимума (УМ): | ||
| + | \[u^*(t) \stackrel{\textrm{п.в.}}{\in} \underset{u \in \cal{P}}{\text{Argmax}} \, \mathcal{H}(\psi^*(t), x^*(t), u(t));\] | ||
| + | 3) \[M(\psi^*(t), x^*(t)) \equiv \text{const} \geqslant 0.\] | ||
| − | ==== Пример | + | '''Доказательство''' принципа максимума Понтрягина можно найти в книге: Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976 [http://control.botik.ru/wp-content/files_mf/1447942876im3547.pdf]. |
| − | + | ||
| + | В общем случае еще учитывается условие трансверсальности на концах, однако поскольку рассматриваемая задача быстродействия является задачей "из точки в точку", их можно опустить. Уточним, что в задаче быстродействия нецелесообразно вводит дополнительную координату в вектор \(x\) и сопряженную переменную \(\psi\), поскольку все условия, связанные с этой дополнительной координатой, равны нулю или не имеют значения. | ||
| + | |||
| + | Важно отметить, что принцип максимума является необходимым, но не достаточным условием. | ||
| + | |||
| + | == Примеры == | ||
| + | |||
| + | === Пример 1 === | ||
| + | Рассмотрим поезд, движущийся по железной дороге. Задача состоит в том, чтобы привести поезд на станцию и остановить его там за кратчайшее время. Положение поезда описывается действительной координатой \(x^1\); начало отсчета \(0\) соответствует станции. Будем считать, что поезд движется без трения, а мы управляем ускорением поезда, прикладывая ограниченную по модулю силу. Подберем единицы измерения так, чтобы максимальное по модулю ускорение было единичным. | ||
| + | Тогда система описывается уравнениями: | ||
\[ | \[ | ||
\begin{cases} | \begin{cases} | ||
| − | \ | + | \ddot{x} = u, \\ |
| − | + | x(0) = x^0, \\ | |
| − | + | x(t_1) = 0; \\ | |
| − | \ | + | u \in [-1, 1]. |
\end{cases} | \end{cases} | ||
\] | \] | ||
| − | + | Или, в стандартном виде: | |
| + | \[ | ||
| + | \begin{cases} | ||
| + | \dot{x}_1 = x_2, \\ | ||
| + | \dot{x}_2 = u, \\ | ||
| + | x_1(0) = x_1^0, \\ | ||
| + | x_2(0) = x_2^0, \\ | ||
| + | x_1(t_1) = 0, \\ | ||
| + | x_2(t_1) = 0, \\ | ||
| + | u \in [-1, 1]. | ||
| + | \end{cases} | ||
| + | \] | ||
| − | + | '''Решение:''' | |
| − | + | Выпишем функцию Гамильтона-Понтрягина: | |
| − | + | \[ | |
| − | + | \mathcal{H} = \psi_1x_2 + \psi_2u. | |
| − | + | \] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Тогда сопряженная система имеет вид: | ||
| + | \[ | ||
| + | \begin{cases} | ||
| + | \dot{\psi}_1 = 0, \\ | ||
| + | \dot{\psi}_2 = -\psi_1. | ||
| + | \end{cases} | ||
| + | \] | ||
| − | + | Из условия максимума имеем, что: | |
| − | |||
\[ | \[ | ||
| − | + | u^*(t) = \text{sgn}\, (\psi_2(t)). | |
\] | \] | ||
| − | + | Поскольку \(\ddot{\psi}_2 = 0\), то \(\psi_2 = \alpha +\beta t \), а значит \(u^*(t) = \text{sgn}\, (\alpha +\beta t)\). Следовательно, \(u(t)\) кусочно постоянно, принимает только экстремальные значения \(\pm 1\) и имеет не более одного переключения (точки разрыва). | |
| + | |||
| + | Отыщем все траектории, соответствующие таким управлениям и приходящие в нуль. Найдем решения следующей системы: | ||
\[ | \[ | ||
| − | + | \begin{cases} | |
| + | \dot{x}_1 = x_2, \\ | ||
| + | \dot{x}_2 = \pm1. | ||
| + | \end{cases} | ||
\] | \] | ||
| − | |||
\[ | \[ | ||
| − | + | x_1 = \pm\frac{x_2^2}{2}+C, C = const | |
\] | \] | ||
| − | + | Из семейства функций, являющихся решением, найдем те, которые не имеют переключений: | |
| − | |||
| − | |||
| − | |||
| − | |||
\[ | \[ | ||
| − | + | x_1 = \frac{x_2^2}{2}, x_2 < 0, \dot{x}_2 > 0; \\ | |
| + | x_1 = -\frac{x_2^2}{2}, x_2 > 0, \dot{x}_2 < 0. | ||
\] | \] | ||
| − | + | Выпишем уравнения для траекторий, когда имеется одно переключение. Пусть \((p, q)\) \(~-\) точка переключения, тогда траектории можно записать как: | |
| − | |||
| − | |||
\[ | \[ | ||
| + | x_1 = | ||
\begin{cases} | \begin{cases} | ||
| − | \ | + | -\frac{x_2^2}{2} + \frac{q^2}{2} + p, x_2 > q, \dot{x}_2 < 0, \\ |
| − | + | \frac{x_2^2}{2}, 0 > x_2 > q, \dot{x}_2 > 0, | |
| − | |||
| − | |||
| − | |||
\end{cases} | \end{cases} | ||
\] | \] | ||
| − | |||
\[ | \[ | ||
| − | \ | + | x_1 = |
| + | \begin{cases} | ||
| + | \frac{x_2^2}{2} - \frac{q^2}{2} + p, x_2 < q, \dot{x}_2 > 0, \\ | ||
| + | -\frac{x_2^2}{2}, 0 < x_2 < q, \dot{x}_2 < 0. | ||
| + | \end{cases} | ||
\] | \] | ||
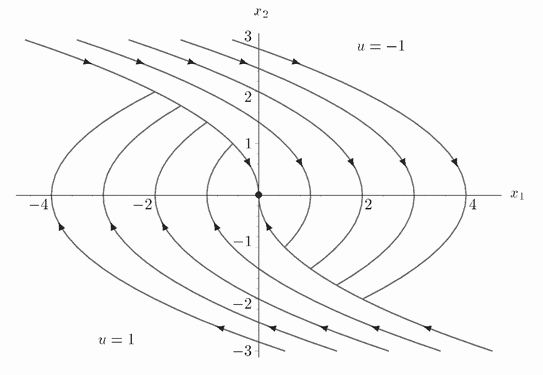
| − | + | Все траектории можно изобразить на графике: | |
| + | |||
| + | [[Файл:grafpng.png|центр|обрамить|Общий вид оптимального синтеза]] | ||
| + | |||
| + | Поскольку через любую точку вида \((x_1, x_2)\) проходит единственная кривая из представленных, то для любой начальной точки существует единственная траектория, переводящая ей в конечную. Оптимальные траектории существуют, значит и решение оптимально. | ||
| − | + | === Пример 2 === | |
| − | + | Решим следующую задачу быстродействия: | |
\[ | \[ | ||
| − | + | \begin{cases} | |
| + | \dot{x}_1 = x_2, \\ | ||
| + | \dot{x}_2 = -x_1 + u, \\ | ||
| + | x(0) = x^0, \\ | ||
| + | x(t_1) = 0; \\ | ||
| + | u \in [-1, 1]. | ||
| + | \end{cases} | ||
\] | \] | ||
| − | + | '''Решение:''' | |
| + | Выпишем функцию Гамильтона-Понтрягина: | ||
| + | \[ | ||
| + | \mathcal{H} = \psi_1x_2 - \psi_2x_1 + \psi_2u. | ||
| + | \] | ||
| − | + | Тогда сопряженная система имеет вид: | |
| + | \[ | ||
| + | \begin{cases} | ||
| + | \dot{\psi}_1 = \psi_2, \\ | ||
| + | \dot{\psi}_2 = -\psi_1. | ||
| + | \end{cases} | ||
| + | \] | ||
| − | + | Из условия максимума имеем, что оптимальное управление: | |
| − | |||
\[ | \[ | ||
| − | + | u^*(t) = \text{sgn}(\psi_2(t)). | |
\] | \] | ||
| − | |||
| − | |||
| − | |||
| − | ==== | + | Так как \(\ddot{\psi}_2 = \psi_2\), то \(\psi_2 = \alpha\, \text{sin}(t+\beta), \alpha, \beta = const\). При этом \(\alpha \neq 0\), поскольку иначе \(\psi_2 = 0 \rightarrow \psi_1 = 0\) (из сопряженной системы) \(~-\) а это противоречит принципу максимума. |
| − | |||
| − | = | + | Поскольку \(u^*(t) = \text{sgn}(\alpha\, \text{sin}(t+\beta))\), то переключения зависят от первого момента переключения \(\tau \in [0, t]\) и изначального знака \(\text{sgn}\, (u^*(0)) \in \{\pm1\} \). Сами переключения будут происходить через каждое \(\pi\) от начального переключения \(\tau\). Оптимальное управление принимает только значение \(\pm 1\), тогда траектории \((x_1(t), x_2(t)\) состоят из кусков, удовлетворяющих системе: |
| − | |||
| − | |||
| − | |||
| − | |||
\[ | \[ | ||
\begin{cases} | \begin{cases} | ||
| − | \dot{x}_1 = | + | \dot{x}_1 = x_2, \\ |
| − | \dot{x}_2 = | + | \dot{x}_2 = -x_1\pm1, |
\end{cases} | \end{cases} | ||
\] | \] | ||
| + | т.е. из дуг окружностей \((x_1 \pm 1)^2 + x_2^2 = C, C = const\). | ||
| − | + | Заметим, что существует закономерность: переключения происходят на полуокружностях | |
| − | + | \[ | |
| − | = | + | (x_1 + 1)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ |
| − | + | (x_1 - 3)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ | |
| − | + | (x_1 + 5)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ | |
| + | (x_1 - 7)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ | ||
| + | \] | ||
| + | и так далее. Таким образом, кривую переключений можно выразить как | ||
\[ | \[ | ||
| − | + | (x_1 + (2k-1))^2 + x_2^2 = 1, x_2 \geqslant 0, k \in \mathbb{N}\\ | |
| + | (x_1 - (2k-1))^2 + x_2^2 = 1, x_2 \leqslant 0, k \in \mathbb{N} \\ | ||
\] | \] | ||
| − | + | ||
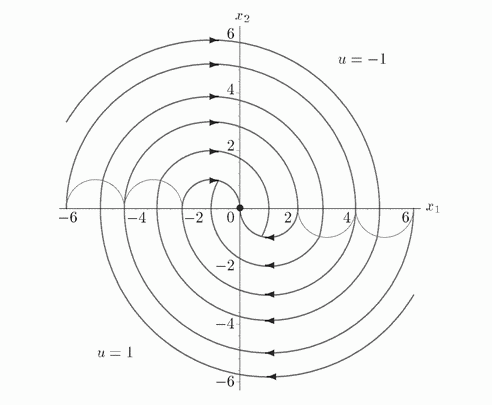
| + | Все траектории можно изобразить на графике: | ||
| + | |||
| + | [[Файл:graf_2.png|центр|обрамить|Оптимальные траектории]] | ||
| + | |||
| + | Поскольку для любой точки вида \((x_1, x_2)\) существует единственная кривая из семейства выше, то можно однозначно восстановить оптимальную траекторию. | ||
| + | |||
| + | == Список литературы == | ||
| + | * Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976, | ||
| + | * А.А. Аграчев, Ю.Л. Сачков. "Геометрическая теория управления". Москва, Физматлит, 2005 | ||
Текущая версия на 22:48, 14 февраля 2023
Содержание
Постановка задачи
Задача быстродействия\(~-\) задача перевода системы из начального фиксированного положения в конечное, также фиксированное, положение за минимальное время.
Пусть наша система описывается следующими условиями: \[ \begin{cases} \dot{x}(t) = f(x(t), u(t)), \\ x(t_0) = x^0, \\ x(t_1) = x^1, \\ u(\tau) \in \mathcal{P}(\tau) \in \text{conv} \, \mathbb{R}^m, \\ t_1 - t_0 \rightarrow \underset{u(\cdot)}{\text{inf}}, \end{cases} \]
где \(x_0, x_1, t_0 \) \(~-\) фиксированы, \(A(t), B(t), f(t) \) \(~-\) непрерывны, а \(\mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \(l: \rho(l\vert\mathcal{P}(\tau)\) по \(\tau\) непрерывна\(^1\)).
\(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P} = [a(\tau), b(\tau)]\); непрерывность многозначного отображения означает, что \(a(\tau), b(\tau)\) - непрерывны.
Заметим, что в общем случае функционал имеет вид: \[ \mathcal{J} = \int\limits_{t_0}^{t_1}f^0(x(t), u(t))\,dt \rightarrow \underset{u(\cdot)}{\text{inf}} \] Принимая \(f^0 \equiv 1 \), получаем задачу быстродействия с функционалом \(\mathcal{J} = t_1 - t_0\).
Сопряженная переменная имеет следующий вид: \(\psi = (\psi_1, ..., \psi_n)\).
Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H}(\psi, x, u) = \langle \psi, f(x(t), u(t)) \rangle. \]
Тогда можно говорить о сопряженной системе: \[ \dot{\psi} = -\frac{\partial \mathcal{H}}{\partial x(t)}. \]
Заметим, что гамильтонианом системы называется \(M = \underset{u\in \mathcal{P}}{\text{sup}} \, \mathcal{H}(\psi, x, u)\). Однако в задаче быстродействия супремум достижим, поэтому \(M = \underset{u\in \mathcal{P}}{\text{max}} \, \langle \psi, f(x(t), u(t)) \rangle\).
Принцип максимума Понтрягина
Теорема(ПМП для автономной задачи быстродействия)
Пусть \((x^*(\cdot), u^*(\cdot))\) \(~-\) оптимальная пара, \(\mathcal{H}\) \(~-\) функция Гамильтона–Понтрягина. Тогда существует \(\psi^*:[t_0, t_1] \rightarrow \mathbb{R}^n \), \(\psi^* \neq 0 \) такое, что:
1) Сопряженная система (СС): \[\dot{\psi} = -\frac{\partial H(\psi(t), x(t), u(t))}{\partial x(t)} \bigg|_{x=x^*(t) \\ u=u^*(t) \\ \psi = \psi^*(t)};\] 2) Условие максимума (УМ): \[u^*(t) \stackrel{\textrm{п.в.}}{\in} \underset{u \in \cal{P}}{\text{Argmax}} \, \mathcal{H}(\psi^*(t), x^*(t), u(t));\] 3) \[M(\psi^*(t), x^*(t)) \equiv \text{const} \geqslant 0.\]
Доказательство принципа максимума Понтрягина можно найти в книге: Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976 [1].
В общем случае еще учитывается условие трансверсальности на концах, однако поскольку рассматриваемая задача быстродействия является задачей "из точки в точку", их можно опустить. Уточним, что в задаче быстродействия нецелесообразно вводит дополнительную координату в вектор \(x\) и сопряженную переменную \(\psi\), поскольку все условия, связанные с этой дополнительной координатой, равны нулю или не имеют значения.
Важно отметить, что принцип максимума является необходимым, но не достаточным условием.
Примеры
Пример 1
Рассмотрим поезд, движущийся по железной дороге. Задача состоит в том, чтобы привести поезд на станцию и остановить его там за кратчайшее время. Положение поезда описывается действительной координатой \(x^1\); начало отсчета \(0\) соответствует станции. Будем считать, что поезд движется без трения, а мы управляем ускорением поезда, прикладывая ограниченную по модулю силу. Подберем единицы измерения так, чтобы максимальное по модулю ускорение было единичным. Тогда система описывается уравнениями: \[ \begin{cases} \ddot{x} = u, \\ x(0) = x^0, \\ x(t_1) = 0; \\ u \in [-1, 1]. \end{cases} \]
Или, в стандартном виде: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = u, \\ x_1(0) = x_1^0, \\ x_2(0) = x_2^0, \\ x_1(t_1) = 0, \\ x_2(t_1) = 0, \\ u \in [-1, 1]. \end{cases} \]
Решение: Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H} = \psi_1x_2 + \psi_2u. \]
Тогда сопряженная система имеет вид: \[ \begin{cases} \dot{\psi}_1 = 0, \\ \dot{\psi}_2 = -\psi_1. \end{cases} \]
Из условия максимума имеем, что: \[ u^*(t) = \text{sgn}\, (\psi_2(t)). \] Поскольку \(\ddot{\psi}_2 = 0\), то \(\psi_2 = \alpha +\beta t \), а значит \(u^*(t) = \text{sgn}\, (\alpha +\beta t)\). Следовательно, \(u(t)\) кусочно постоянно, принимает только экстремальные значения \(\pm 1\) и имеет не более одного переключения (точки разрыва).
Отыщем все траектории, соответствующие таким управлениям и приходящие в нуль. Найдем решения следующей системы: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = \pm1. \end{cases} \]
\[ x_1 = \pm\frac{x_2^2}{2}+C, C = const \]
Из семейства функций, являющихся решением, найдем те, которые не имеют переключений: \[ x_1 = \frac{x_2^2}{2}, x_2 < 0, \dot{x}_2 > 0; \\ x_1 = -\frac{x_2^2}{2}, x_2 > 0, \dot{x}_2 < 0. \]
Выпишем уравнения для траекторий, когда имеется одно переключение. Пусть \((p, q)\) \(~-\) точка переключения, тогда траектории можно записать как:
\[ x_1 = \begin{cases} -\frac{x_2^2}{2} + \frac{q^2}{2} + p, x_2 > q, \dot{x}_2 < 0, \\ \frac{x_2^2}{2}, 0 > x_2 > q, \dot{x}_2 > 0, \end{cases} \]
\[ x_1 = \begin{cases} \frac{x_2^2}{2} - \frac{q^2}{2} + p, x_2 < q, \dot{x}_2 > 0, \\ -\frac{x_2^2}{2}, 0 < x_2 < q, \dot{x}_2 < 0. \end{cases} \]
Все траектории можно изобразить на графике:
Поскольку через любую точку вида \((x_1, x_2)\) проходит единственная кривая из представленных, то для любой начальной точки существует единственная траектория, переводящая ей в конечную. Оптимальные траектории существуют, значит и решение оптимально.
Пример 2
Решим следующую задачу быстродействия: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = -x_1 + u, \\ x(0) = x^0, \\ x(t_1) = 0; \\ u \in [-1, 1]. \end{cases} \]
Решение: Выпишем функцию Гамильтона-Понтрягина: \[ \mathcal{H} = \psi_1x_2 - \psi_2x_1 + \psi_2u. \]
Тогда сопряженная система имеет вид: \[ \begin{cases} \dot{\psi}_1 = \psi_2, \\ \dot{\psi}_2 = -\psi_1. \end{cases} \]
Из условия максимума имеем, что оптимальное управление: \[ u^*(t) = \text{sgn}(\psi_2(t)). \]
Так как \(\ddot{\psi}_2 = \psi_2\), то \(\psi_2 = \alpha\, \text{sin}(t+\beta), \alpha, \beta = const\). При этом \(\alpha \neq 0\), поскольку иначе \(\psi_2 = 0 \rightarrow \psi_1 = 0\) (из сопряженной системы) \(~-\) а это противоречит принципу максимума.
Поскольку \(u^*(t) = \text{sgn}(\alpha\, \text{sin}(t+\beta))\), то переключения зависят от первого момента переключения \(\tau \in [0, t]\) и изначального знака \(\text{sgn}\, (u^*(0)) \in \{\pm1\} \). Сами переключения будут происходить через каждое \(\pi\) от начального переключения \(\tau\). Оптимальное управление принимает только значение \(\pm 1\), тогда траектории \((x_1(t), x_2(t)\) состоят из кусков, удовлетворяющих системе: \[ \begin{cases} \dot{x}_1 = x_2, \\ \dot{x}_2 = -x_1\pm1, \end{cases} \] т.е. из дуг окружностей \((x_1 \pm 1)^2 + x_2^2 = C, C = const\).
Заметим, что существует закономерность: переключения происходят на полуокружностях \[ (x_1 + 1)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ (x_1 - 3)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ (x_1 + 5)^2 + x_2^2 = 1, x_2 \geqslant 0, \\ (x_1 - 7)^2 + x_2^2 = 1, x_2 \leqslant 0, \\ \] и так далее. Таким образом, кривую переключений можно выразить как \[ (x_1 + (2k-1))^2 + x_2^2 = 1, x_2 \geqslant 0, k \in \mathbb{N}\\ (x_1 - (2k-1))^2 + x_2^2 = 1, x_2 \leqslant 0, k \in \mathbb{N} \\ \]
Все траектории можно изобразить на графике:
Поскольку для любой точки вида \((x_1, x_2)\) существует единственная кривая из семейства выше, то можно однозначно восстановить оптимальную траекторию.
Список литературы
- Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976,
- А.А. Аграчев, Ю.Л. Сачков. "Геометрическая теория управления". Москва, Физматлит, 2005