Матрица Якоби. Лемма о выпрямлении векторного поля: различия между версиями
Nikita23 (обсуждение | вклад) |
Nikita23 (обсуждение | вклад) |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 14: | Строка 14: | ||
В частном случае, при <math> m = 1 </math> матрица Якоби состоит из одной строки: этот вектор называется '''градиентом''' функции <math> f(x_1, \dots, x_n) </math> в точке <math> | В частном случае, при <math> m = 1 </math> матрица Якоби состоит из одной строки: этот вектор называется '''градиентом''' функции <math> f(x_1, \dots, x_n) </math> в точке <math> | ||
\bar{x} = (\bar{x}_1, \dots, \bar{x}_n): </math>: | \bar{x} = (\bar{x}_1, \dots, \bar{x}_n): </math>: | ||
| − | <math> grad \ f(\bar{x}) = \begin{pmatrix} | + | <math> \mathrm{grad} \ f(\bar{x}) = \begin{pmatrix} |
\dfrac{\partial{f}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f}}{\partial{x_n}}(\bar{x}) \\ | \dfrac{\partial{f}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f}}{\partial{x_n}}(\bar{x}) \\ | ||
\end{pmatrix}. | \end{pmatrix}. | ||
| Строка 22: | Строка 22: | ||
[https://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B8%D1%82%D0%B5%D0%BB%D1%8C определитель] называется '''якобианом''' или '''определителем Якоби''' или '''функциональным определителем''' системы из <math> n </math> функций <math> \{f_1(x_1, x_2, \dots, x_n), \dots, f_n(x_1, x_2, \dots, x_n) \} </math> по переменным <math> x_1, \dots, x_n: </math>: | [https://ru.wikipedia.org/wiki/%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B8%D1%82%D0%B5%D0%BB%D1%8C определитель] называется '''якобианом''' или '''определителем Якоби''' или '''функциональным определителем''' системы из <math> n </math> функций <math> \{f_1(x_1, x_2, \dots, x_n), \dots, f_n(x_1, x_2, \dots, x_n) \} </math> по переменным <math> x_1, \dots, x_n: </math>: | ||
<math> | <math> | ||
| − | \mathcal{J}(x_1, \dots, x_n) = \ | + | \mathcal{J}(x_1, \dots, x_n) = \det D_x{f}(x)= \begin{vmatrix} |
\dfrac{\partial{f_1}}{\partial{x_1}}(x) & \dfrac{\partial{f_1}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_1}}{\partial{x_n}}(x) \\ | \dfrac{\partial{f_1}}{\partial{x_1}}(x) & \dfrac{\partial{f_1}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_1}}{\partial{x_n}}(x) \\ | ||
\dfrac{\partial{f_2}}{\partial{x_1}}(x) & \dfrac{\partial{f_2}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_2}}{\partial{x_n}}(x) \\ | \dfrac{\partial{f_2}}{\partial{x_1}}(x) & \dfrac{\partial{f_2}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_2}}{\partial{x_n}}(x) \\ | ||
| Строка 31: | Строка 31: | ||
== Теорема о локальной обратимости == | == Теорема о локальной обратимости == | ||
| − | * <math> Y \subset \mathbb{R}^n </math> | + | '''Теорема 1.''' |
| + | |||
| + | $$\quad$$ Пусть нам известно, что | ||
| + | * <math> Y \subset \mathbb{R}^n </math> — [https://ru.wikipedia.org/wiki/%D0%9E%D1%82%D0%BA%D1%80%D1%8B%D1%82%D0%BE%D0%B5_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE открытое множество]; | ||
* <math> g(y): Y \rightarrow \mathbb{R}^n </math>, непрерывна вместе со своими частными производными в <math> Y</math>; | * <math> g(y): Y \rightarrow \mathbb{R}^n </math>, непрерывна вместе со своими частными производными в <math> Y</math>; | ||
| − | * | + | * якобиан <math> \det D_y g(y) \neq 0 \ \forall y \in Y</math>. |
| − | Тогда <math> g(y) </math> локально обратима, то есть <math> \forall y_0 \in Y | + | Тогда <math> g(y) </math> локально обратима, то есть <math> \forall y_0 \in Y </math> существует открытое множество <math> Y_0: y_0 \in Y_0 \subset Y</math> и |
[https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F обратное отображение] <math> (g(y)|_{Y_0})^{-1}: X_0 \rightarrow Y_0 </math>, где <math> X_0 = g(Y_0)</math>. <br> | [https://ru.wikipedia.org/wiki/%D0%9E%D0%B1%D1%80%D0%B0%D1%82%D0%BD%D0%B0%D1%8F_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D1%8F обратное отображение] <math> (g(y)|_{Y_0})^{-1}: X_0 \rightarrow Y_0 </math>, где <math> X_0 = g(Y_0)</math>. <br> | ||
''Доказательство.'' <br> | ''Доказательство.'' <br> | ||
| − | Зафиксируем <math> \forall y_0 \in Y</math>. Обозначим <math> x_0 = g(y_0) </math>. <math> F(x, y)</math> примем равным <math> g(y) - x</math>. Применим к ней теорему о неявной функции | + | Зафиксируем <math> \forall y_0 \in Y</math>. Обозначим <math> x_0 = g(y_0) </math>. <math> F(x, y)</math> примем равным <math> g(y) - x</math>. Применим к ней [[#Используемые теоремы|теорему о неявной функции]], для этого покажем выполнимость её условий: |
# <math> F(x_0, y_0) = g(y_0) - x_0 = 0</math>. | # <math> F(x_0, y_0) = g(y_0) - x_0 = 0</math>. | ||
| − | # <math> F(x, y)</math> | + | # <math> F(x, y)</math> — непрерывна вместе со своими частными производными в окрестности точки <math> (x_0, y_0)</math> из условия. |
| − | # Якобиан <math> \det D_y{F(x_0, y_0)} = \det | + | # Якобиан <math> \det D_y{F(x_0, y_0)} = \det D_y{g(y_0)} \neq 0</math> по условию. |
Поэтому <math> \exists \gamma > 0, \delta > 0 </math> и непрерывно дифференцируемая функция <math> \phi: U_{\gamma}(x_0) \rightarrow U_{\delta}(y_0)</math> такая, что: | Поэтому <math> \exists \gamma > 0, \delta > 0 </math> и непрерывно дифференцируемая функция <math> \phi: U_{\gamma}(x_0) \rightarrow U_{\delta}(y_0)</math> такая, что: | ||
<math> \forall x \in U_{\gamma}(x_0), y \in U_{\delta}(y_0) \Rightarrow y = \phi(x) \Leftrightarrow F(x, y) = 0 \Leftrightarrow g(y) = x. </math> | <math> \forall x \in U_{\gamma}(x_0), y \in U_{\delta}(y_0) \Rightarrow y = \phi(x) \Leftrightarrow F(x, y) = 0 \Leftrightarrow g(y) = x. </math> | ||
| − | Таким образом, мы | + | Таким образом, мы доказали, что для <math> x</math> и <math> y</math>, взятых из данных достаточно малых окрестностей, у функции <math> g(y)</math> существует обратная к ней <math> \phi(x) </math>. |
$$\blacksquare$$ | $$\blacksquare$$ | ||
== Лемма о выпрямлении векторного поля == | == Лемма о выпрямлении векторного поля == | ||
| − | Пусть нам задана система: | + | '''Лемма.''' |
| − | <math> \dfrac | + | |
| + | $$\quad$$ Пусть нам задана система: | ||
| + | <math> \dfrac{d x_i}{dt} = f_i(x_1, \dots, x_n), \ \ \ i = \overline{1, n}, </math> | ||
с непрерывно дифференцируемой правой частью <math> f(x)</math> и некоторая [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B нестационарная точка] <math> a </math> (<math>f(a) \neq 0 </math>), тогда найдётся такая окрестность <math> U(a)</math> и новые координаты <math> y_1, \dots, y_n</math>, для которых <math> x_i = \psi_i(y_1, \dots, y_n) </math>, такие, что: | с непрерывно дифференцируемой правой частью <math> f(x)</math> и некоторая [https://sawiki.cs.msu.ru/index.php/%D0%9D%D0%B5%D0%BF%D0%BE%D0%B4%D0%B2%D0%B8%D0%B6%D0%BD%D1%8B%D0%B5_%D1%82%D0%BE%D1%87%D0%BA%D0%B8_%D1%81%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D1%8B нестационарная точка] <math> a </math> (<math>f(a) \neq 0 </math>), тогда найдётся такая окрестность <math> U(a)</math> и новые координаты <math> y_1, \dots, y_n</math>, для которых <math> x_i = \psi_i(y_1, \dots, y_n) </math>, такие, что: | ||
| − | <math> \dfrac{ | + | <math> \dfrac{dy_i}{dt} = 0, \dfrac{dy_n}{dt} = 1, \ \ \ i = \overline{1, n-1}.</math> |
''Доказательство.'' <br> | ''Доказательство.'' <br> | ||
| − | + | Будем считать, что <math> f_n(a) \neq 0 </math> (пользуемся тем, что <math> f(a) \neq 0 </math>). Рассмотрим задачу Коши: | |
<math> | <math> | ||
\begin{equation}\label{eq1} | \begin{equation}\label{eq1} | ||
\begin{cases} | \begin{cases} | ||
| − | \dfrac{ | + | \dfrac{dx_i}{dt} = f_i(x_1, \dots, x_n), \ \ \ i = \overline{1, n}, \\ |
x_1(0) = \xi_1, \ \dots, \ x_{n-1}(0) = \xi_{n-1}, \ x_n(0) = a_n. | x_1(0) = \xi_1, \ \dots, \ x_{n-1}(0) = \xi_{n-1}, \ x_n(0) = a_n. | ||
\end{cases} | \end{cases} | ||
| Строка 62: | Строка 67: | ||
</math> | </math> | ||
Обозначим за <math> a' </math> первые <math> n - 1 </math> координаты точки <math> a </math>, а <math> \xi' </math> примем равным <math> (\xi_1, \dots, \xi_{n-1}),</math> причём <math> \xi' </math> будем брать из <math> U(a') </math>. Тогда система <math> \eqref{eq1}</math> задаёт в зависимости от начальных условий фазовую траекторию, которую выпустили с <math> U(a) \cap \{ x \ | \ x_n = a_n \}</math>. Тут важно отметить, что в силу <math> \dot{x}_n(a) \neq 0</math>, нам достаточно анализировать только траектории, лежащие в малой окрестности точки <math> a </math>, пересекающие <math> \{ x \ | \ x_n = a_n \}</math>, ведь в случае касания обнуляется производная, а случай, когда решение не имеет общих точек с рассматриваемой [https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%BF%D0%B5%D1%80%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D1%8C гиперплоскостью], но лежит в окрестности <math> a </math>, считаем несущественным, так как будет понятно в дальнейшем: на выпрямление векторного поля он не влияет. | Обозначим за <math> a' </math> первые <math> n - 1 </math> координаты точки <math> a </math>, а <math> \xi' </math> примем равным <math> (\xi_1, \dots, \xi_{n-1}),</math> причём <math> \xi' </math> будем брать из <math> U(a') </math>. Тогда система <math> \eqref{eq1}</math> задаёт в зависимости от начальных условий фазовую траекторию, которую выпустили с <math> U(a) \cap \{ x \ | \ x_n = a_n \}</math>. Тут важно отметить, что в силу <math> \dot{x}_n(a) \neq 0</math>, нам достаточно анализировать только траектории, лежащие в малой окрестности точки <math> a </math>, пересекающие <math> \{ x \ | \ x_n = a_n \}</math>, ведь в случае касания обнуляется производная, а случай, когда решение не имеет общих точек с рассматриваемой [https://ru.wikipedia.org/wiki/%D0%93%D0%B8%D0%BF%D0%B5%D1%80%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D1%8C гиперплоскостью], но лежит в окрестности <math> a </math>, считаем несущественным, так как будет понятно в дальнейшем: на выпрямление векторного поля он не влияет. | ||
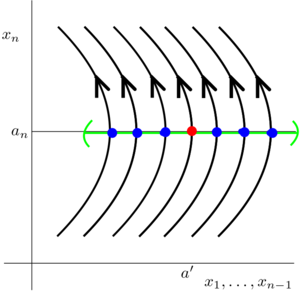
| − | [[Файл: | + | [[Файл:Traj_2.png|300px|thumb|right|Изначальное векторное поле в окрестности точки <math> a </math>. Зелёным цветом изображено <math> U(a) \cap \{ x \ | \ x_n = a_n \}</math>]] |
| − | + | Приведённые рассуждения позволяют провести | |
[https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%B5%D0%BA%D1%86%D0%B8%D1%8F взаимнооднозначное соответствие] между "существенными" траекториями из окрестности точки <math> a </math> и координатами их пересечений с <math> \{ x \ | \ x_n = a_n \}</math> (воспользовались тем, что в фазовом пространстве решения не пересекаются), что в совокупности с параметризацией по времени позволяет нам целиком восстанавливать решения. <br> | [https://ru.wikipedia.org/wiki/%D0%91%D0%B8%D0%B5%D0%BA%D1%86%D0%B8%D1%8F взаимнооднозначное соответствие] между "существенными" траекториями из окрестности точки <math> a </math> и координатами их пересечений с <math> \{ x \ | \ x_n = a_n \}</math> (воспользовались тем, что в фазовом пространстве решения не пересекаются), что в совокупности с параметризацией по времени позволяет нам целиком восстанавливать решения. <br> | ||
| − | Формализуем проведённый выше анализ и отталкиваясь от него докажем лемму. Взаимнооднозначное соответствие представим как <math> x(t | + | Формализуем проведённый выше анализ и отталкиваясь от него докажем лемму. Взаимнооднозначное соответствие представим как <math> x(t, (\xi', a_n)) = \psi(t, \xi')</math>, а начальные условия <math> \eqref{eq1}</math> перепишем в виде <math> \psi_i(0, \xi') = \xi_i, \ \ \ i = \overline{1, n-1}, \psi_n(0, \xi') = a_n </math> (в момент времени 0 находимся в точке <math> (\xi', a_n) </math>). Теперь покажем, что <math> y_i = \xi_i, \ i = \overline{1, n-1}, y_n = t </math> является искомой заменой координат, то есть, что в новых координатах получается требуемая система дифференциальных уравнений и якобиан перехода не вырожден (замена корректна).: |
| − | <math> \dfrac{ | + | <math> \dfrac{dy_i}{dt} = 0, \ \ \ i = \overline{1, n-1}, </math> |
| − | поскольку со временем координата пересечения траектории с <math> \{ x \ | \ x_n = a_n \}</math> не изменяется. <math> \dfrac{ | + | поскольку со временем координата пересечения траектории с <math> \{ x \ | \ x_n = a_n \}</math> не изменяется. <math> \dfrac{dy_n}{dt} = 1,</math> по построению. <br> |
| − | Корректность замены. Из того, что у исходной системы уравнений гладкая правая часть, мы можем воспользоваться теоремой о непрерывной дифференцируемости решений задачи Коши по начальным значениям и в совокупности с определением <math> x(t | + | Корректность замены. Из того, что у исходной системы уравнений гладкая правая часть, мы можем воспользоваться [[#Используемые теоремы| теоремой о непрерывной дифференцируемости решений задачи Коши по начальным значениям]] и в совокупности с определением <math> x(t, (\xi', a_n)) = \psi(t, \xi')</math>, получить, что <math> \psi_i(t, \xi')</math> имеет непрерывные частные производные в прообразе <math> U(a)</math>. Это в свою очередь является [[#Используемые теоремы| достаточным условием дифференцируемости]]. Вычислим значения частных производных: |
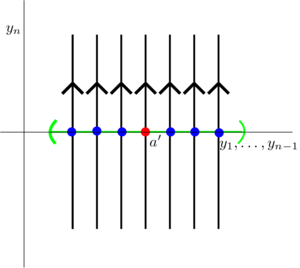
| − | [[Файл: | + | [[Файл:Traj_1.png|300px|thumb|right|Прямое векторное поле после замены координат]]: |
<math> | <math> | ||
\dfrac{\partial{\psi}_i}{\partial{y}_j}\bigg{|}_{t = 0} = \delta_{ij}, \ \ \ i = \overline{1, n}, j = \overline{1, n-1}, | \dfrac{\partial{\psi}_i}{\partial{y}_j}\bigg{|}_{t = 0} = \delta_{ij}, \ \ \ i = \overline{1, n}, j = \overline{1, n-1}, | ||
</math> | </math> | ||
| − | так как частные производные берём не по <math> n</math>-ой координате, то можем её значение <math> y_n = t = 0</math> подставить в числитель сразу | + | так как частные производные берём не по <math> n</math>-ой координате, то можем её значение <math> y_n = t = 0</math> подставить в числитель сразу <math>( \psi_i(0, y') = \xi_i = y_i )</math>. <math> \delta_{ij}</math> — это [https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%B2%D0%BE%D0%BB_%D0%9A%D1%80%D0%BE%D0%BD%D0%B5%D0%BA%D0%B5%D1%80%D0%B0 символ Кронекера]. : |
<math> | <math> | ||
| − | \dfrac{\partial{\psi}_n}{\partial{y}_n}\bigg{|}_{t = 0} = \dfrac{\partial{\psi}_n}{\partial{t}}\bigg{|}_{t = 0} = \bigg{\{} \dfrac{ | + | \dfrac{\partial{\psi}_n}{\partial{y}_n}\bigg{|}_{t = 0} = \dfrac{\partial{\psi}_n}{\partial{t}}\bigg{|}_{t = 0} = \bigg{\{} \dfrac{dx_n}{dt} = \sum_{k=1}^{n}{\dfrac{\partial{\psi}_n}{\partial{y}_k}} \dfrac{d{y}_k}{d{t}} = \dfrac{\partial{\psi}_n}{\partial{t}} \bigg{\}} = \dfrac{d{x}_n}{d{t}}\bigg{|}_{t = 0} = f_n(\xi', a_n) \neq 0, |
</math> | </math> | ||
окрестность <math> U(a)</math> подбирается таким образом, чтобы в ней сохранялось <math> f_n(\xi', a_n) \neq 0 </math>. Записывая якобиан для замены переменных в момент времени <math> t = 0</math>, получим: | окрестность <math> U(a)</math> подбирается таким образом, чтобы в ней сохранялось <math> f_n(\xi', a_n) \neq 0 </math>. Записывая якобиан для замены переменных в момент времени <math> t = 0</math>, получим: | ||
<math> | <math> | ||
| − | \ | + | \det D_y\psi(0, \xi') = \begin{vmatrix} |
1 & 0 & \dots & 0 & * \\ | 1 & 0 & \dots & 0 & * \\ | ||
0 & 1 & \dots & 0 & * \\ | 0 & 1 & \dots & 0 & * \\ | ||
| Строка 88: | Строка 93: | ||
</math> | </math> | ||
Подытожим некоторые факты, доказанные выше: | Подытожим некоторые факты, доказанные выше: | ||
| − | # <math> \psi(y)</math> является непрерывной вместе со своими частными производными для <math> y</math>, соответствующих прообразу <math> U(a)</math> | + | # <math> \psi(y)</math> является непрерывной вместе со своими частными производными для <math> y</math>, соответствующих прообразу <math> U(a)</math>. |
| − | # Якобиан <math> \det | + | # Якобиан <math> \det D_y\psi(0, \xi') \neq 0</math>. |
| − | + | Что позволяет нам использовать [[#Теорема о локальной обратимости| теорему о локальной обратимости]] для функции <math> \psi(y) </math> в окрестности точки <math> y_0 = (a', 0) </math> и тем самым завершить доказательство. | |
$$\blacksquare$$ | $$\blacksquare$$ | ||
== Используемые теоремы == | == Используемые теоремы == | ||
| − | '''Теорема | + | '''Теорема 2.''' (О неявной функции) |
| − | + | ||
| − | + | $$\quad$$ Пусть | |
| − | + | * <math> F_1(x, y_1, \dots, y_m), \dots, F_m(x, y_1, \dots, y_m)</math> непрерывны в окрестности точки <math> (x^0, y_1^0, \dots, y_m^0) </math> вместе со своими частными производными; | |
| + | * <math> F_i(x^0, y_1^0, \dots, y_m^0) = 0, i = \overline{1, m}</math>; | ||
| + | * якобиан <math> \det D_y{F(x^0, y_1^0, \dots, y_m^0)} \neq 0</math>. | ||
Тогда существует окрестность точки <math> (x^0, y_1^0, \dots, y_m^0) </math>, в которой | Тогда существует окрестность точки <math> (x^0, y_1^0, \dots, y_m^0) </math>, в которой | ||
<math> y = \phi(x) \Leftrightarrow F(x, y) = 0 </math> и, кроме того, функции <math> \phi_i(x), i = \overline{1, m}</math> непрерывно дифференцируемы в окрестности точки <math> x^0</math>. | <math> y = \phi(x) \Leftrightarrow F(x, y) = 0 </math> и, кроме того, функции <math> \phi_i(x), i = \overline{1, m}</math> непрерывно дифференцируемы в окрестности точки <math> x^0</math>. | ||
| − | '''Теорема | + | '''Теорема 3.''' (О непрерывной дифференцируемости решений задачи Коши по начальным данным) |
| − | + | ||
| − | + | $$\quad$$ Рассмотрим в области <math> Q_{\mu} = \{ (t, y, \mu): |t - t_0| \leqslant T, \ A \leqslant y \leqslant B, \ \mu_1 \leqslant \mu \leqslant \mu_2 \}</math> задачу Коши: | |
<math> | <math> | ||
\begin{cases} | \begin{cases} | ||
| Строка 111: | Строка 118: | ||
\end{cases} | \end{cases} | ||
</math> | </math> | ||
| − | * | + | Пусть для неё выполняются следующие условия |
| − | * | + | * <math> f(t, y, \mu)</math> непрерывна в <math> Q_{\mu}</math> и имеет в <math> Q_{\mu}</math> непрерывные частные производные <math> f_y(t, y, \mu), f_{\mu}(t, y, \mu)</math>; |
| − | Тогда, если <math> y(t, \mu)</math> | + | * функция <math> y_0(\mu)</math> непрерывно дифференцируема на отрезке <math> [\mu_1, \mu_2] </math>. |
| + | Тогда, если <math> y(t, \mu)</math> — решение задачи Коши на отрезке <math> [t_0 - T, t_0 + T]</math> для всех <math> \mu \in [\mu_1, \mu_2]</math>, то функция <math> y(t, \mu)</math> имеет в <math> t \in [t_0 - T, t_0 + T], \mu \in [\mu_1, \mu_2]</math> непрерывную производную по <math> \mu </math>. | ||
| − | '''Теорема | + | '''Теорема 4.''' (Достаточное условие дифференцируемости) |
| − | Если функция определена на множестве и имеет в точке непрерывные частные производные по всем переменным, то она в этой точке дифференцируема. | + | |
| + | $$\quad$$ Если функция определена на множестве и имеет в точке непрерывные частные производные по всем переменным, то она в этой точке дифференцируема. | ||
==Список литературы== | ==Список литературы== | ||
| Строка 122: | Строка 131: | ||
#Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011. | #Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011. | ||
#Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023. | #Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023. | ||
| − | + | #Федорюк М.В. Обыкновенные дифференциальные уравнения, М.: Наука, 1985 | |
<math> </math> | <math> </math> | ||
Текущая версия на 01:53, 19 декабря 2023
Содержание
Определение и основные свойства
Матрицей Якоби, системы из \( m \) функций \( \{f_1(x_1, x_2, \dots, x_n), \dots, f_m(x_1, x_2, \dots, x_n) \} \) по переменным
\( x_1, \dots, x_n \) в точке \( \bar{x} = (\bar{x}_1, \dots, \bar{x}_n) \) называется матрица, составленная из всевозможных
частных производных
этих функций, взятых в рассматриваемой точке\[
J(\bar{x}) = \begin{pmatrix}
\dfrac{\partial{f_1}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f_1}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f_1}}{\partial{x_n}}(\bar{x}) \\
\dfrac{\partial{f_2}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f_2}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f_2}}{\partial{x_n}}(\bar{x}) \\
\dots & \dots & \dots & \dots \\
\dfrac{\partial{f_m}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f_m}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f_m}}{\partial{x_n}}(\bar{x}) \\
\end{pmatrix}.
\]
В частном случае, при \( m = 1 \) матрица Якоби состоит из одной строки: этот вектор называется градиентом функции \( f(x_1, \dots, x_n) \) в точке \(
\bar{x} = (\bar{x}_1, \dots, \bar{x}_n): \)\[ \mathrm{grad} \ f(\bar{x}) = \begin{pmatrix}
\dfrac{\partial{f}}{\partial{x_1}}(\bar{x}) & \dfrac{\partial{f}}{\partial{x_2}}(\bar{x}) & \dots & \dfrac{\partial{f}}{\partial{x_n}}(\bar{x}) \\
\end{pmatrix}.
\]
Можно сказать, что в общем случае системы функций их матрица Якоби состоит из строк, являющихся градиентами этих функций.
В другом частном случае, когда \( m = n \), матрица Якоби становится квадратной и тогда ее
определитель называется якобианом или определителем Якоби или функциональным определителем системы из \( n \) функций \( \{f_1(x_1, x_2, \dots, x_n), \dots, f_n(x_1, x_2, \dots, x_n) \} \) по переменным \( x_1, \dots, x_n: \)\[
\mathcal{J}(x_1, \dots, x_n) = \det D_x{f}(x)= \begin{vmatrix}
\dfrac{\partial{f_1}}{\partial{x_1}}(x) & \dfrac{\partial{f_1}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_1}}{\partial{x_n}}(x) \\
\dfrac{\partial{f_2}}{\partial{x_1}}(x) & \dfrac{\partial{f_2}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_2}}{\partial{x_n}}(x) \\
\dots & \dots & \dots & \dots \\
\dfrac{\partial{f_n}}{\partial{x_1}}(x) & \dfrac{\partial{f_n}}{\partial{x_2}}(x) & \dots & \dfrac{\partial{f_n}}{\partial{x_n}}(x) \\
\end{vmatrix}.
\]
Теорема о локальной обратимости
Теорема 1.
$$\quad$$ Пусть нам известно, что
- \( Y \subset \mathbb{R}^n \) — открытое множество;
- \( g(y): Y \rightarrow \mathbb{R}^n \), непрерывна вместе со своими частными производными в \( Y\);
- якобиан \( \det D_y g(y) \neq 0 \ \forall y \in Y\).
Тогда \( g(y) \) локально обратима, то есть \( \forall y_0 \in Y \) существует открытое множество \( Y_0: y_0 \in Y_0 \subset Y\) и
обратное отображение \( (g(y)|_{Y_0})^{-1}: X_0 \rightarrow Y_0 \), где \( X_0 = g(Y_0)\).
Доказательство.
Зафиксируем \( \forall y_0 \in Y\). Обозначим \( x_0 = g(y_0) \). \( F(x, y)\) примем равным \( g(y) - x\). Применим к ней теорему о неявной функции, для этого покажем выполнимость её условий:
- \( F(x_0, y_0) = g(y_0) - x_0 = 0\).
- \( F(x, y)\) — непрерывна вместе со своими частными производными в окрестности точки \( (x_0, y_0)\) из условия.
- Якобиан \( \det D_y{F(x_0, y_0)} = \det D_y{g(y_0)} \neq 0\) по условию.
Поэтому \( \exists \gamma > 0, \delta > 0 \) и непрерывно дифференцируемая функция \( \phi: U_{\gamma}(x_0) \rightarrow U_{\delta}(y_0)\) такая, что\[ \forall x \in U_{\gamma}(x_0), y \in U_{\delta}(y_0) \Rightarrow y = \phi(x) \Leftrightarrow F(x, y) = 0 \Leftrightarrow g(y) = x. \] Таким образом, мы доказали, что для \( x\) и \( y\), взятых из данных достаточно малых окрестностей, у функции \( g(y)\) существует обратная к ней \( \phi(x) \). $$\blacksquare$$
Лемма о выпрямлении векторного поля
Лемма.
$$\quad$$ Пусть нам задана система\[ \dfrac{d x_i}{dt} = f_i(x_1, \dots, x_n), \ \ \ i = \overline{1, n}, \]
с непрерывно дифференцируемой правой частью \( f(x)\) и некоторая нестационарная точка \( a \) (\(f(a) \neq 0 \)), тогда найдётся такая окрестность \( U(a)\) и новые координаты \( y_1, \dots, y_n\), для которых \( x_i = \psi_i(y_1, \dots, y_n) \), такие, что\[ \dfrac{dy_i}{dt} = 0, \dfrac{dy_n}{dt} = 1, \ \ \ i = \overline{1, n-1}.\]
Доказательство.
Будем считать, что \( f_n(a) \neq 0 \) (пользуемся тем, что \( f(a) \neq 0 \)). Рассмотрим задачу Коши\[
\begin{equation}\label{eq1}
\begin{cases}
\dfrac{dx_i}{dt} = f_i(x_1, \dots, x_n), \ \ \ i = \overline{1, n}, \\
x_1(0) = \xi_1, \ \dots, \ x_{n-1}(0) = \xi_{n-1}, \ x_n(0) = a_n.
\end{cases}
\end{equation}
\]
Обозначим за \( a' \) первые \( n - 1 \) координаты точки \( a \), а \( \xi' \) примем равным \( (\xi_1, \dots, \xi_{n-1}),\) причём \( \xi' \) будем брать из \( U(a') \). Тогда система \( \eqref{eq1}\) задаёт в зависимости от начальных условий фазовую траекторию, которую выпустили с \( U(a) \cap \{ x \ | \ x_n = a_n \}\). Тут важно отметить, что в силу \( \dot{x}_n(a) \neq 0\), нам достаточно анализировать только траектории, лежащие в малой окрестности точки \( a \), пересекающие \( \{ x \ | \ x_n = a_n \}\), ведь в случае касания обнуляется производная, а случай, когда решение не имеет общих точек с рассматриваемой гиперплоскостью, но лежит в окрестности \( a \), считаем несущественным, так как будет понятно в дальнейшем: на выпрямление векторного поля он не влияет.
Приведённые рассуждения позволяют провести
взаимнооднозначное соответствие между "существенными" траекториями из окрестности точки \( a \) и координатами их пересечений с \( \{ x \ | \ x_n = a_n \}\) (воспользовались тем, что в фазовом пространстве решения не пересекаются), что в совокупности с параметризацией по времени позволяет нам целиком восстанавливать решения.
Формализуем проведённый выше анализ и отталкиваясь от него докажем лемму. Взаимнооднозначное соответствие представим как \( x(t, (\xi', a_n)) = \psi(t, \xi')\), а начальные условия \( \eqref{eq1}\) перепишем в виде \( \psi_i(0, \xi') = \xi_i, \ \ \ i = \overline{1, n-1}, \psi_n(0, \xi') = a_n \) (в момент времени 0 находимся в точке \( (\xi', a_n) \)). Теперь покажем, что \( y_i = \xi_i, \ i = \overline{1, n-1}, y_n = t \) является искомой заменой координат, то есть, что в новых координатах получается требуемая система дифференциальных уравнений и якобиан перехода не вырожден (замена корректна).\[ \dfrac{dy_i}{dt} = 0, \ \ \ i = \overline{1, n-1}, \]
поскольку со временем координата пересечения траектории с \( \{ x \ | \ x_n = a_n \}\) не изменяется. \( \dfrac{dy_n}{dt} = 1,\) по построению.
Корректность замены. Из того, что у исходной системы уравнений гладкая правая часть, мы можем воспользоваться теоремой о непрерывной дифференцируемости решений задачи Коши по начальным значениям и в совокупности с определением \( x(t, (\xi', a_n)) = \psi(t, \xi')\), получить, что \( \psi_i(t, \xi')\) имеет непрерывные частные производные в прообразе \( U(a)\). Это в свою очередь является достаточным условием дифференцируемости. Вычислим значения частных производных:
\[ \dfrac{\partial{\psi}_i}{\partial{y}_j}\bigg{|}_{t = 0} = \delta_{ij}, \ \ \ i = \overline{1, n}, j = \overline{1, n-1}, \]
так как частные производные берём не по \( n\)-ой координате, то можем её значение \( y_n = t = 0\) подставить в числитель сразу \(( \psi_i(0, y') = \xi_i = y_i )\). \( \delta_{ij}\) — это символ Кронекера. \[ \dfrac{\partial{\psi}_n}{\partial{y}_n}\bigg{|}_{t = 0} = \dfrac{\partial{\psi}_n}{\partial{t}}\bigg{|}_{t = 0} = \bigg{\{} \dfrac{dx_n}{dt} = \sum_{k=1}^{n}{\dfrac{\partial{\psi}_n}{\partial{y}_k}} \dfrac{d{y}_k}{d{t}} = \dfrac{\partial{\psi}_n}{\partial{t}} \bigg{\}} = \dfrac{d{x}_n}{d{t}}\bigg{|}_{t = 0} = f_n(\xi', a_n) \neq 0, \] окрестность \( U(a)\) подбирается таким образом, чтобы в ней сохранялось \( f_n(\xi', a_n) \neq 0 \). Записывая якобиан для замены переменных в момент времени \( t = 0\), получим\[ \det D_y\psi(0, \xi') = \begin{vmatrix} 1 & 0 & \dots & 0 & * \\ 0 & 1 & \dots & 0 & * \\ \dots & \dots & \dots & \dots & \dots \\ 0 & 0& \dots & 1 & * \\ 0 & 0 & \dots & 0 & f_n(\xi', a_n) \\ \end{vmatrix} = f_n(\xi', a_n) \neq 0. \] Подытожим некоторые факты, доказанные выше:
- \( \psi(y)\) является непрерывной вместе со своими частными производными для \( y\), соответствующих прообразу \( U(a)\).
- Якобиан \( \det D_y\psi(0, \xi') \neq 0\).
Что позволяет нам использовать теорему о локальной обратимости для функции \( \psi(y) \) в окрестности точки \( y_0 = (a', 0) \) и тем самым завершить доказательство. $$\blacksquare$$
Используемые теоремы
Теорема 2. (О неявной функции)
$$\quad$$ Пусть
- \( F_1(x, y_1, \dots, y_m), \dots, F_m(x, y_1, \dots, y_m)\) непрерывны в окрестности точки \( (x^0, y_1^0, \dots, y_m^0) \) вместе со своими частными производными;
- \( F_i(x^0, y_1^0, \dots, y_m^0) = 0, i = \overline{1, m}\);
- якобиан \( \det D_y{F(x^0, y_1^0, \dots, y_m^0)} \neq 0\).
Тогда существует окрестность точки \( (x^0, y_1^0, \dots, y_m^0) \), в которой \( y = \phi(x) \Leftrightarrow F(x, y) = 0 \) и, кроме того, функции \( \phi_i(x), i = \overline{1, m}\) непрерывно дифференцируемы в окрестности точки \( x^0\).
Теорема 3. (О непрерывной дифференцируемости решений задачи Коши по начальным данным)
$$\quad$$ Рассмотрим в области \( Q_{\mu} = \{ (t, y, \mu): |t - t_0| \leqslant T, \ A \leqslant y \leqslant B, \ \mu_1 \leqslant \mu \leqslant \mu_2 \}\) задачу Коши\[ \begin{cases} y'(t) = f(t, y, \mu), \\ y(t_0) = y_0(\mu). \end{cases} \] Пусть для неё выполняются следующие условия
- \( f(t, y, \mu)\) непрерывна в \( Q_{\mu}\) и имеет в \( Q_{\mu}\) непрерывные частные производные \( f_y(t, y, \mu), f_{\mu}(t, y, \mu)\);
- функция \( y_0(\mu)\) непрерывно дифференцируема на отрезке \( [\mu_1, \mu_2] \).
Тогда, если \( y(t, \mu)\) — решение задачи Коши на отрезке \( [t_0 - T, t_0 + T]\) для всех \( \mu \in [\mu_1, \mu_2]\), то функция \( y(t, \mu)\) имеет в \( t \in [t_0 - T, t_0 + T], \mu \in [\mu_1, \mu_2]\) непрерывную производную по \( \mu \).
Теорема 4. (Достаточное условие дифференцируемости)
$$\quad$$ Если функция определена на множестве и имеет в точке непрерывные частные производные по всем переменным, то она в этой точке дифференцируема.
Список литературы
- Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
- Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.
- Федорюк М.В. Обыкновенные дифференциальные уравнения, М.: Наука, 1985
\( \)