Преобразование Лапласа: различия между версиями
Janus (обсуждение | вклад) м |
Janus (обсуждение | вклад) |
||
| Строка 170: | Строка 170: | ||
== Вычисление обратного преобразования Лапласа == | == Вычисление обратного преобразования Лапласа == | ||
| − | [[File:Analit_pict.PNG| | + | [[File:Analit_pict.PNG|300px|thumb|right|.]] |
Рассмотрим формулу Меллина \eqref{Mellins_formula}: | Рассмотрим формулу Меллина \eqref{Mellins_formula}: | ||
\[ | \[ | ||
f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp | f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp | ||
| + | \] | ||
| + | |||
| + | В области $$\mu > \mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, \dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} \overset{\Omega_R}{\underset{\R \to +\infty}{\rightrightarrows}} 0$$. Отсюда получаем: | ||
| + | \[ | ||
| + | f(t)\chi(t) = \frac{1}{2\pi i } \cdot 2\pi i \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) = \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) | ||
\] | \] | ||
Версия 19:46, 23 ноября 2020
Преобразование Лапласа — интегральное преобразование, связывающее функцию $$F(p)$$ комплексного переменного (изображение) с функцией $$f(t)$$ вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения. Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так, свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование
Преобразованием Лапласа действительнозначной функции $$f(t)$$ называется функция $$F(p)$$ комплексной переменной такая, что
\begin{equation}\label{intLapl} \boxed{F(p) = \int\limits^{+\infty}_0 f(t) e^{-pt} dt, \quad p \in \mathbb(C).} \end{equation}
Правая часть этого выражения называется интегралом Лапласа.
Для преобразования Лапласа используется обозначение $$f(t) \supset F(t)$$
Выясним, при каких условиях существует интеграл Лапласа для заданной функции $$f(t)$$. Будем рассматривать функцию $$f_\mu(t) = e^{-\mu t} f(t)$$, $$\mu \in \mathbb{R}$$. Пусть существуют константы $$A$$, $$\mu_0$$ такие, что $$|f(t)| \le Ae^{-\mu_0 t}$$ $$\forall t\ge T$$. Тогда для любого $$\mu \ge \mu_0$$ $$\exists \int\limits_0^{+\infty} |e^{-\mu t} f(t)|dt < \infty$$. Поставим в соответствие функции $$f_\mu(t)$$ функцию $$F_\mu(t)$$, определяемую как прямое преобразование Фурье функции $$f_\mu(t)$$: $$F_\mu(t) = \int\limits_0^{+\infty} f_\mu(t) e^{-i\omega t} dt = \int\limits_0^{+\infty} f(t) e^{-\mu t} e^{-i\omega t} dt = \left\{\text{обозначим } p = \mu + i\omega\in \mathbb{C}\right\} = \int\limits_0^{+\infty} f(t) e^{-pt} dt \equiv F(p)$$.
Получаем следующие достаточные условия существования прямого преобразования Лапласа:
- функция $$f$$ растёт не быстрее показательной функции, т.е.
\begin{equation}\label{growth_cond} \exists A, \mu_0 \text{ такие, что } |f(t)|\le Ae^{-\mu_0 t} \quad \forall t\ge T \end{equation}
- интеграл $$\int\limits_0^{+\infty}|f(t) dt|$$ существует и конечен.
Обратное преобразование
Будем рассматривать физически реализуемую функцию $$\chi(t)f_\mu(t)$$, где функция $$\chi(t)$$ — функция Хевисайда: \[ \chi(t) = \left\{\begin{align*} 1,\ &t\ge0,\\ 0,\ &t<0. \end{align*}\right. \]
В этом случае $$t$$ может иметь смысл времени, поэтому получаем, что функция $$f(t)\chi(t)$$ задана только на положительной полуоси $$t\ge0$$.
Рассмотрим обратное преобразование Фурье от функции $$F_\mu(\omega)$$: \[ f(t) e^{-\mu t} \chi(t) = f_\mu(t) \chi(t) = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F_\mu(\omega) e^{i\omega t} dt = \frac{1}{2\pi} \int\limits_{-\infty}^{+\infty} F(p) e^{i\omega t} dt. \]
Сделаем замену $$p = \mu + i\omega$$. Тогда $$d\omega = \frac{dp}{i}$$, а верхний и нижний пределы интегрирования равны: $$\omega = +\infty \Rightarrow p = \mu + i\infty$$, $$\omega = -\infty \Rightarrow p = \mu - i\infty$$. Получаем:
\[ f(t) e^{-\mu t} \chi(t) = \frac{1}{2\pi i} e^{-\mu t} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p) e^{pt} dp \quad \forall \mu > \tilde{\mu}. \]
Домножив обе части равенства на $$e^{\mu t}$$, окончательно получим формулу обратного преобразования Лапласа:
\begin{equation}\label{Mellins_formula} \boxed{f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu-i\infty}^{\mu+i\infty} F(p)e^{pt} dp.} \end{equation}
Правая часть этого выражения называется формулой Меллина.
Теорема об области существовании изображения
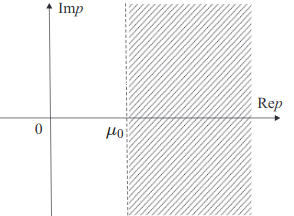
Для всякого оригинала $$f(t)$$ изображение по Лапласу $$F(p)$$ определено в полуплоскости \(\mathrm{Re} p > \mu_0\) и является в этой области аналитической функцией.
Доказательство. Докажем, сначала, что интеграл Лапласа \eqref{intLapl} сходится абсолютно в области $$\mathrm{Re} p = \mu > \mu_0$$. В силу общего признака сравнения и условия роста \eqref{growth_cond} получаем, что
\[ \left|\int\limits_0^{+\infty} f(t) e^{pt} dt\right| \le \int\limits_0^{+\infty} |f(t)| e^{-\mu t} dt < A \int\limits_0^{+\infty} e^{-(\mu-\mu_0)t} dt. \]
Итак, для $$\mu>\mu_0$$: \begin{equation}\label{int_bounds} \left| \int\limits_0^{+\infty} f(t) e^{-pt} dt \right| < \frac{A}{\mu-\mu_0}, \end{equation} то есть интеграл Лапласа сходится абсолютно.
Докажем теперь существование производной несобственного интеграла \eqref{intLapl} по параметру $$p$$. Для этого убедимся в равномерной сходимости в области $$\mathrm{Re}\,p > \mu_0$$ интеграла \[ F'(p) = J(p) = \int\limits_0^{+\infty} (-t) f(t) e^{(\mu + i\omega)t} dt \]
Выберем произвольное положительное действительное число $$\mu_1$$ такое, что $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. Тогда, в соответствии с признаком Вейерштрасса равномерной сходимости получаем, что
\[ |J(p)| \le \int\limits_0^{+\infty} t |f(t)| e^{-\mu_1 t} dt < A\int\limits_0^{+\infty} t e^{-(\mu_1-\mu_0)t} dt = \frac{A}{(\mu_1-\mu_0)^2} < \infty, \]
что и доказывает возможность дифференцирования интеграла \eqref{intLapl} по параметру $$p$$ в области $$\mathrm{Re}\,p \ge \mu_1 > \mu_0$$. В силу произвольности выбора $$\mu_1$$ мы доказали аналитичность изображения в области $$\mathrm{Re}\,p > \mu_0$$. $$\blacksquare$$
Замечание. Из неравенства \eqref{int_bounds} вытекает, что $$\lim\limits_{\mu \to +\infty} F(p) = 0$$. Отсюда следует, что изображение $$F(p)\to 0$$ при $$p \to \infty$$, оставаясь внутри угла $$-\frac{\pi}{2} + \delta < \arg p < \frac{\pi}{2} - \delta$$, где $$\delta$$ — сколь угодно малое положительное число. Если же функция $$F(p)$$ аналитична в бесконечно удалённой точке $$p=\infty$$, то $$F(p)\to\infty$$ при $$p\to\infty$$ по любому пути.
Элементарные преобразования
| $$f(t) \chi(t)$$ | $$F(t)$$ |
|---|---|
| \[1\] | \[\frac{1}{p}\] |
| \[ e^{\beta t} \] | \[ \frac{1}{p-\beta} \] |
| \[ f(t)e^{\beta t} \] | \[ F(p-\beta) \] |
| \[ f(t)e^{-\beta t} \] | \[ F(\beta-p) \] |
| \[ t^\alpha e^{\beta t} \] | \[ \frac{\Gamma(\alpha + 1)}{(p-\beta)^{\alpha + 1}} \] |
| \[ t^n, n\in\mathbb{N} \] | \[ \frac{n!}{p^{n+1}} \] |
| \[ t^\alpha, \alpha\in\mathbb{R} \] | \[ \frac{\Gamma(\alpha+1)}{p^{\alpha+1}} \] |
| \[ \sin \beta t \] | \[ \frac{\beta}{p^2+\beta^2} \] |
| \[ \cos \beta t \] | \[ \frac{p}{p^2+\beta^2} \] |
| \[ t^\alpha \sin \beta t \] | \[ \frac{\Gamma(\alpha + 1)}{2i}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} - \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] |
| \[ t^\alpha \cos \beta t \] | \[ \frac{\Gamma(\alpha + 1)}{2}\left( \frac{1}{(p-i\beta)^{\alpha + 1}} + \frac{1}{(p + i\beta)^{\alpha+1}} \right) \] |
| \[ \sinh t \] | \[ \frac{\beta}{p^2-\beta^2} \] |
| \[ \cosh t \] | \[ \frac{p}{p^2-\beta^2} \] |
| \[ t^\alpha \sinh t \] | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} - \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] |
| \[ t^\alpha \cosh t \] | \[ \frac{\Gamma(\alpha + 1)}{2} \left( \frac{1}{(p-\beta)^{\alpha + 1}} + \frac{1}{(p+\beta)^{\alpha + 1}} \right) \] |
| \[ \delta \] | \[ 1 \] |
Приведём доказательства для некоторых из этих формул.
- Пусть $$f(t)=1$$.
\[ \int\limits_0^{+\infty} t e^{-pt} dt = \left. -\frac{1}{p} e^{-pt} \right|^{+\infty}_0 = \frac{1}{p}. \]
Легко видеть, что данный интеграл сходится при любом $$\mu>0$$ - Пусть теперь $$f(t) \supset F(p)$$.
\[ \int\limits_0^{+\infty} f(t) e^{(\beta-p)t} dt = F(p-\beta). \] - Найдём преобразование Лапласа для функции $$f(t) = \chi(t) t^\alpha$$, $$\alpha > 0$$.
\[ \forall p\in\mathbb{R} : \int\limits_0^{+\infty} t^\alpha e^{-\pt} dt = \left\{ \begin{matrix} pt = s \\ ds = pdt \end{matrix} \right\} = \int\limits_0^{+\infty} \left( \frac{s}{p} \right)^\alpha e^{-s} \frac{1}{p} ds = \frac{1}{p^{\alpha + 1}} \int\limits_0^{+\infty} s^\alpha e^{-s} ds = \frac{1}{p^{\alpha + 1}} \Gamma(\alpha + 1). \]
Эту функцию можно аналитически продолжить на всю комплексную плоскость, т.е. \[ \forall p\in\mathbb{C} : \chi(t) t^\alpha \supset \frac{\Gamma(\alpha + 1)}{p^{\alpha + 1}} \quad \forall \alpha > 0. \] - Рассмотрим функции $$\chi(t) t^\alpha \cos \beta t$$ и $$\chi(t) t^\alpha \sin \beta t$$. По формуле Эйлера: \[
\cos \beta t = \frac{e^{i\beta t} + e^{-i\beta t}}{2}, \quad \sin \beta t = \frac{e^{i\beta t} - e^{-i\beta t}}{2}
\]
Отсюда, используя результаты пункта 3, легко получить формулы изображений для указанных функций.
Аналогично выводятся формулы для гиперболических тригонометрических функций: \[ \sinh x = \frac{e^x - e^{-x}}{2}, \quad \cosh x = \frac{e^x + e^{-x}}{2} \]
Свойства преобразования Лапласа
Будем обозначать через $$F(p)$$, $$G(p)$$, $$H(p)$$ и т.д. изображения по Лапласу оригиналов $$f(t)$$, $$g(t)$$, $$h(t)$$ и тд.
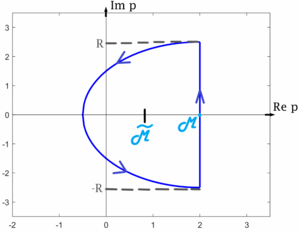
Вычисление обратного преобразования Лапласа
Рассмотрим формулу Меллина \eqref{Mellins_formula}: \[ f(t)\chi(t) = \frac{1}{2\pi i} \int\limits_{\mu - i\infty}^{\mu + i\infty} F(p)e^{pt} dp \]
В области $$\mu > \mu_0$$ функция $$F(p)$$ является аналитичной (по теореме об области существования). Пусть функция $$F(p)$$ имеет конечное число особых точек $$p_1, p_2, \dots, p_n$$, лежащих в конечной части плоскости (т.е. существует такая полуокружность, которая содержит все эти особые точки). Тогда для этой функции применима лемма Жордана, то есть $$F(p) e^{pt} \overset{\Omega_R}{\underset{\R \to +\infty}{\rightrightarrows}} 0$$. Отсюда получаем: \[ f(t)\chi(t) = \frac{1}{2\pi i } \cdot 2\pi i \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) = \sum\limits_{i=1}^n \mathbb{res}\,(F(p)e^{pt}, p_i) \]