Фазовые и интегральные кривые. Фазовое пространство

Множество всевозможных состояний динамической системы называется фазовым пространством этой системы.

Пусть дана динамическая система: \begin{equation} \label{eq:0} \frac{du}{dt} = f(u),\ u \in U \subseteq \mathbb{R}^n,\ f:U \rightarrow \mathbb{R}^n,\ f \in C^2(U). \end{equation} Множество $$U$$ возможных состояний $$u$$ - фазовое пространство системы \eqref{eq:0}.

Обозначим за $$u = u(t; u_0)$$ решение системы \eqref{eq:0} с начальным условием $$u(0) = u_0$$. Множество точек $${t, u(t; u0)}$$ называется интегральной кривой системы \eqref{eq:0}, а множество точек $${u(t; u0)}$$ называется фазовой кривой системы \eqref{eq:0}.

Интегральные кривые дают полную информацию о поведении решений системы \eqref{eq:0}, а вот фазовые кривые эту информацию не дают, так как являются лишь проекциями интегральных кривых на фазовое пространство. Но в большинстве случаев достаточно изучить фазовые кривые.

Свойства фазовых кривых

Свойство 1. Две фазовые кривые либо не имеют общих точек, либо совпадают. Это свойство означает, что фазовое пространство расслаивается на непересекающиеся фазовые кривые.

Свойство 2. Если точка $$u^*$$ -- неподвижная точка системы \eqref{eq:0}, то точка $$u = u^*$$ есть фазовая кривая.

Свойство 3. Фазовая кривая, отличная от точки, есть гладкая кривая, то есть в каждой точке имеется ненулевой касательный вектор, непрерывно зависящий от длины дуги.

Свойство 4. Всякая фазовая кривая принадлежит одному из трех типов: гладкая кривая без самопересечений; замкнутая гладкая кривая (цикл); точка.

Цикл - периодическая траектория, не являющаяся положением равновесия, каждая точка которой удовлетворяет условию $$u(t + T_0; u_0) = u(t; u_0)$$ для некоторого $$T_0 > 0$$ и всех $$t \in \mathbb{R}$$.

Примеры

Пример 1.

Пример 1. Интегральная кривая в пространстве $$(u_1, u_2, t)$$ системы из примера 1. На плоскости $$(u_1, u_2)$$ изображена фазовая кривая системы при начальном условии $$u(0) = u_0$$, она является неподвижной точкой (0,0) и циклом, обозначенным как $$\gamma(u_0)$$, указано направление фазового потока.

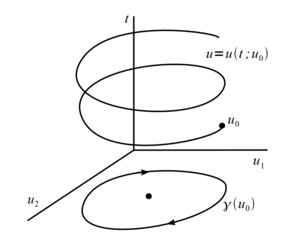
Рассмотрим следующую динамическую систему \begin{equation} \label{eq:1} \begin{cases} \dot{u}_1 = u_2 ,\\ \dot{u}_2 = -u_1. \end{cases} \end{equation} Общее решение имеет вид $$u_1(t) = C\ \sin(t + \alpha_0), u_2(t) = C\ \cos(t + \alpha_0)$$, где C и $$\alpha_0$$ — постоянные, определяемые начальными условиями. Интегральная кривая представляет собой винтовую линию, намотанную на цилиндр $$u_1^2+u_2^2 = C^2$$ в пространстве $$(u_1, u_2, t)$$. Фазовые кривые системы \eqref{eq:1} являются окружностями $$u_1^2+u_2^2 = C^2$$ в фазовом пространстве $$(u_1, u_2)$$.

Пример 2.

Пример 2. Интегральные кривые уравнения (3) для различных значений $$N_0$$ в плоскости $$(t, N)$$. На оси N также изображены неподвижные точки (жирные точки) и направления фазового потока.

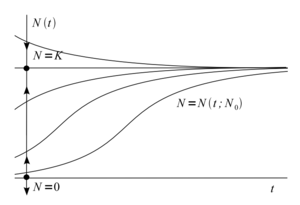
Рассмотрим одномерную динамическую систему, задаваемую логистическим уравнением \begin{equation} \label{eq:2} \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right). \end{equation} Решение системы при начальном условии $$N=N_0$$ представляется следующим образом: \begin{equation} \label{eq:3} N(t) = \dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . \end{equation} Фазовое пространство в этом случае одномерно. Стрелками отмечено направление движения фазового потока на оси $$N$$. Фазовые траектории системы представляют собой отрезки прямой $$N$$, движение по которым происходит в направлении точки с координатой $$K$$.

Список литературы

1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.

2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.