Фазовый объём. Теорема Лиувилля: различия между версиями
Konst23 (обсуждение | вклад) |
Konst23 (обсуждение | вклад) |
||
| (не показано 27 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
== Определения == | == Определения == | ||
'''Определение 1.''' | '''Определение 1.''' | ||
| − | [[Файл: | + | [[Файл:Pred_png_1.png|300px|right]] |
Пусть рассматривается система обыкновенных дифференциальных уравнений: | Пусть рассматривается система обыкновенных дифференциальных уравнений: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \frac{dx_i}{dt}=f_i(x),\quad \text{где}\quad x\in \mathbb{R}^n\ | + | \frac{dx_i}{dt}=f_i(x),\quad \text{где}\quad x=(x_1,...,x_n)\in \mathbb{R}^n,\\ |
| + | f_i(x)\: — \text{ компоненты вектор-функции } f(x)=\big(f_1(x),...,f_n(x)\big);\\ | ||
x(0)=x_0\in D_0. | x(0)=x_0\in D_0. | ||
\end{gather*} | \end{gather*} | ||
Введём обозначение для множества решений системы в фиксированный момент времени: | Введём обозначение для множества решений системы в фиксированный момент времени: | ||
\begin{gather*} | \begin{gather*} | ||
| − | D_t=\left\{\,x( | + | D_t=\left\{\,x(t,x_0),\quad x_0\in D_0\right\}. |
\end{gather*} | \end{gather*} | ||
| − | + | '''Фазовым объёмом''' множества $$D_t$$ называется выражение, определяемое по [https://ru.wikipedia.org/wiki/Кратный_интеграл интегральной] формуле: | |
| − | \begin{ | + | \begin{equation} |
%V_t=\underbrace{\int...\int}_{D_t} dx_1\,dx_2...dx_n. | %V_t=\underbrace{\int...\int}_{D_t} dx_1\,dx_2...dx_n. | ||
| + | \label{eq:0} | ||
V_t=\int\limits_{D_t} dx_1 dx_2...dx_n.\\ | V_t=\int\limits_{D_t} dx_1 dx_2...dx_n.\\ | ||
| − | \end{ | + | \end{equation} |
| − | |||
<br> | <br> | ||
'''Определение 2.''' | '''Определение 2.''' | ||
| − | Величина $$\ | + | Величина $$\dfrac{dV_t}{dt}$$ называется '''изменением фазового объёма.''' |
== Вспомогательные леммы == | == Вспомогательные леммы == | ||
'''Лемма 1.''' (Уравнение в вариациях) | '''Лемма 1.''' (Уравнение в вариациях) | ||
| Строка 26: | Строка 27: | ||
$$\quad$$ Пусть задана система обыкновенных дифференциальных уравнений: | $$\quad$$ Пусть задана система обыкновенных дифференциальных уравнений: | ||
\begin{equation} | \begin{equation} | ||
| − | \label{1} | + | \label{eq:1} |
| − | \frac{dx}{dt}=f(x),\quad \text{где}\quad x\in \mathbb{R}^n\quad \text{и}\quad f\ | + | \frac{dx}{dt}=f(x),\quad \text{где}\quad x=(x_1,...,x_n)\in \mathbb{R}^n \quad \text{и}\quad f(x)=\big(f_1(x),...,f_n(x)\big); |
\end{equation} | \end{equation} | ||
\begin{equation} | \begin{equation} | ||
| + | \label{eq:2} | ||
x(0)=y, \quad y\in D_0. | x(0)=y, \quad y\in D_0. | ||
\end{equation} | \end{equation} | ||
[[Файл:pic1.jpg|200px|thumb|right]] | [[Файл:pic1.jpg|200px|thumb|right]] | ||
| − | Считаем, что $$x(t | + | Считаем, что $$x(t,y)$$ — решение системы \eqref{eq:1}-\eqref{eq:2} является дважды непрерывно дифференцируемой вектор-функцией в некоторой области, в которой и происходит рассмотрение леммы. |
| − | + | Запишем матрицу чувствительности начальных данных: | |
\begin{gather*} | \begin{gather*} | ||
| − | &\frac{\partial x(t | + | &\frac{\partial x(t,y)}{\partial y}=\bigg(\frac{\partial x_i}{\partial y_j}\bigg)_{i,j=\overline{1,n}}= |
| − | &\frac{\partial | + | \begin{pmatrix} |
| + | \frac{\partial x_1}{\partial y_1}& \frac{\partial x_1}{\partial y_2}& ... & \frac{\partial x_1}{\partial y_n}\\ | ||
| + | \frac{\partial x_2}{\partial y_1}& \frac{\partial x_2}{\partial y_2}& ... & \frac{\partial x_2}{\partial y_n}\\ | ||
| + | ...&...&...&...\\ | ||
| + | \frac{\partial x_n}{\partial y_1}& \frac{\partial x_n}{\partial y_2}& ... & \frac{\partial x_n}{\partial y_n}\\ | ||
| + | \end{pmatrix}. | ||
\end{gather*} | \end{gather*} | ||
| − | $$\ | + | В этой матрице $$\dfrac{\partial x_i}{\partial y_j}$$ — скорость изменения координаты $$x_i$$ в зависимости от начального значения $$y_j.$$ |
| − | + | Запишем ещё одну матрицу: | |
| + | \begin{gather*} | ||
| + | &\frac{\partial f}{\partial x}=\bigg(\frac{\partial f_i}{\partial x_j}\bigg)_{i,j=\overline{1,n}}= | ||
| + | \begin{pmatrix} | ||
| + | \frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& ... & \frac{\partial f_1}{\partial x_n}\\ | ||
| + | \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& ... & \frac{\partial f_2}{\partial x_n}\\ | ||
| + | ...&...&...&...\\ | ||
| + | \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& ... & \frac{\partial f_n}{\partial x_n}\\ | ||
| + | \end{pmatrix}. | ||
| + | \end{gather*} | ||
| − | Тогда справедливо матричное равенство (уравнение в вариациях): | + | Тогда лемма утверждает, что справедливо матричное равенство (уравнение в вариациях): |
| − | \begin{ | + | \begin{gather*} |
| − | \frac{d}{dt}\bigg(\frac{\partial x(t | + | \frac{d}{dt}\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)=\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg). |
| − | \end{ | + | \end{gather*} |
''Доказательство''. | ''Доказательство''. | ||
| + | Распишем покомпонентно систему \eqref{eq:1}: | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | \frac{dx_i(t,y)}{dt}=f_i\big(x(t,y)\big) \quad \bigg| \cdot \frac{\partial}{\partial y_j}\\ | |
| − | \frac{\partial}{\partial y_j}\frac{ | + | \frac{\partial}{\partial y_j}\bigg(\frac{dx_i(t,y)}{dt}\bigg)=\frac{\partial}{\partial y_j}\Big(f_i\big(x(t,y)\big)\Big).\\ |
| − | |||
\end{gather*} | \end{gather*} | ||
| + | [https://ru.wikipedia.org/wiki/Равенство_смешанных_производных Переставим операции] местами, в силу достаточной гладкости функции: | ||
| + | \begin{gather*} | ||
| + | \frac{d}{dt}\bigg(\frac{\partial x_i(t,y)}{\partial y_j}\bigg)=\frac{\partial}{\partial y_j}\Big(f_i\big(x(t,y)\big)\Big)=\\ | ||
| + | =\sum\limits_{s=1}^n \frac{\partial f_i}{\partial x_s} \cdot \frac{\partial x_s}{\partial y_j}=\bigg(\frac{\partial f_i}{\partial x_1},...,\frac{\partial f_i}{\partial x_n}\bigg)\cdot\bigg(\frac{\partial x_1}{\partial y_j},...,\frac{\partial x_n}{\partial y_j}\bigg)^T=\frac{\partial f_i}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y_j}\bigg). | ||
| + | \end{gather*} | ||
| + | Таким образом, получили: | ||
| + | \begin{gather*} | ||
| + | \frac{d}{dt}\bigg(\frac{\partial x_i(t,y)}{\partial y_j}\bigg)=\frac{\partial f_i}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y_j}\bigg), \quad \forall i,j=\overline{1,n}. | ||
| + | \end{gather*} | ||
| + | Получили то, что мы и хотели доказать. | ||
$$\blacksquare$$ | $$\blacksquare$$ | ||
| Строка 64: | Строка 90: | ||
'''Лемма 2.''' (Лиувилля, о дифференцировании [https://ru.wikipedia.org/wiki/Определить определителя]) | '''Лемма 2.''' (Лиувилля, о дифференцировании [https://ru.wikipedia.org/wiki/Определить определителя]) | ||
| − | $$\quad$$ Пусть задана матрица $$A=\big(a_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}.$$ | + | $$\quad$$ Пусть задана матрица $$A(t)=\big(a_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}.$$ |
| − | + | Напомним, что $$\tr A=\sum\limits_{i=1}^n a_{ii}$$ — [https://ru.wikipedia.org/wiki/След_матрицы след] матрицы $$A.$$ | |
Тогда справедливо следующее равенство: | Тогда справедливо следующее равенство: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \frac{d}{dt}|A(t)|=|A(t)|\cdot | + | \frac{d}{dt}|A(t)|=|A(t)|\cdot \tr\big(A^{'}(t)A^{-1}(t)\big), \text{ где } A^{'}(t)=\big(a^{'}_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}=\bigg(\frac{d a_{ij}(t)}{dt}\bigg)\bigg|_{i,j=\overline{1,n}}. |
\end{gather*} | \end{gather*} | ||
''Доказательство''. | ''Доказательство''. | ||
| − | |||
| − | |||
По формуле [https://ru.wikipedia.org/wiki/Ряд_Тейлора Тейлора] имеем: | По формуле [https://ru.wikipedia.org/wiki/Ряд_Тейлора Тейлора] имеем: | ||
| Строка 85: | Строка 109: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \big|E+\underbrace{A^{'}(t)A^{-1}(t)}_{b_{ij}}\Delta t+\bar{o}(\Delta t)\big|= | + | \big|E+\underbrace{A^{'}(t)A^{-1}(t)}_{B(t)=\big(b_{ij}(t)\big)}\Delta t+\bar{o}(\Delta t)\big|= |
\begin{vmatrix} | \begin{vmatrix} | ||
| − | 1+b_{11}\Delta t& b_{12}\Delta t& ... & b_{1n}\Delta t\\ | + | 1+b_{11}\Delta t+\bar{o}(\Delta t)& b_{12}\Delta t+\bar{o}(\Delta t)& ... & b_{1n}\Delta t+\bar{o}(\Delta t)\\ |
| − | b_{21}\Delta t& 1+b_{22}\Delta t& ... & b_{2n}\Delta t\\ | + | b_{21}\Delta t+\bar{o}(\Delta t)& 1+b_{22}\Delta t+\bar{o}(\Delta t)& ... & b_{2n}\Delta t+\bar{o}(\Delta t)\\ |
...&...&...&...\\ | ...&...&...&...\\ | ||
| − | b_{n1}\Delta t | + | b_{n1}\Delta t+\bar{o}(\Delta t)& b_{n2}\Delta t+\bar{o}(\Delta t)& ... & 1+b_{nn}\Delta t+\bar{o}(\Delta t)\\ |
| − | + | \end{vmatrix}. | |
| − | |||
\end{gather*} | \end{gather*} | ||
| − | + | Так как определитель матрицы представляет собой [https://ru.wikipedia.org/wiki/Определитель_матрицы сумму] всевозможных произведений элементов матрицы, взятых ровно по одному из каждой строки и из каждого столбца, получаем: | |
\begin{gather*} | \begin{gather*} | ||
| − | \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=\frac{\big|A(t)\big|\cdot \big(1+\Delta t \cdot | + | \big|E+B(t)\Delta t+\bar{o}(\Delta t)\big|=1+\Delta t\cdot \tr\big(A^{'}(t)A^{-1}(t)\big)+\bar{o}(\Delta t).\\ |
| − | \lim\limits_{\Delta t\to 0} \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t} | + | \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=\frac{\big|A(t)\big|\cdot \big(1+\Delta t \cdot \tr\big(A^{'}(t)A^{-1}(t)\big)+\bar{o}(\Delta t)-1\big)}{\Delta t}=|A(t)|\cdot \big(\tr(A^{'}(t)A^{-1}(t))+\bar{o}(1)\big).\\ |
| + | \frac{d}{dt}|A(t)|=\lim\limits_{\Delta t\to 0} \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=|A(t)|\cdot \tr\big(A^{'}(t)A^{-1}(t)\big). | ||
\end{gather*} | \end{gather*} | ||
| − | |||
$$\blacksquare$$ | $$\blacksquare$$ | ||
| Строка 105: | Строка 128: | ||
'''Теорема.''' | '''Теорема.''' | ||
| − | $$\quad$$ Пусть задана система | + | $$\quad$$ Пусть задана система \eqref{eq:1} с начальным условием \eqref{eq:2}. |
| − | \ | + | |
| − | \ | ||
| − | |||
| − | |||
Также заданы множества решений системы в фиксированные моменты времени: | Также заданы множества решений системы в фиксированные моменты времени: | ||
\begin{gather*} | \begin{gather*} | ||
| − | D_t=\left\{\,x( | + | D_t=\left\{\,x(t,y),\quad y\in D_0\right\}. |
| − | |||
\end{gather*} | \end{gather*} | ||
| + | Определим по формуле \eqref{eq:0} соответствующие фазовые объёмы $$V_t$$ для множеств $$D_t.$$ В частности, фазовый объём множества $$D_0$$ обозначим через $$V_0.$$ | ||
| + | |||
Тогда верна следующая формула для нахождения изменения фазового объёма: | Тогда верна следующая формула для нахождения изменения фазового объёма: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \frac{d V_t}{dt}=\int\limits_{D_t} div\, f\, dx_t,\quad \text{ где }\quad d x_t=dx_1\,dx_2\,...\,dx_n. | + | \frac{d V_t}{dt}=\int\limits_{D_t} \div\, f\, dx_t,\quad \text{ где }\quad d x_t=dx_1\,dx_2\,...\,dx_n. |
\end{gather*} | \end{gather*} | ||
Напомним определение [https://ru.wikipedia.org/wiki/Дивергенция дивиргенции] векторного поля $$f:$$ | Напомним определение [https://ru.wikipedia.org/wiki/Дивергенция дивиргенции] векторного поля $$f:$$ | ||
\begin{gather*} | \begin{gather*} | ||
| − | div\, f=\sum\limits_{i=1}^n \frac{\partial f_i}{\partial x_i}(x). | + | \div\, f=\sum\limits_{i=1}^n \frac{\partial f_i}{\partial x_i}(x). |
\end{gather*} | \end{gather*} | ||
''Доказательство''. | ''Доказательство''. | ||
| − | |||
| − | |||
\begin{gather*} | \begin{gather*} | ||
| − | dx_t=dx_1(t | + | dx_t=dx_1(t,y)\,dx_2(t,y)\,...\, dx_n(t,y)=\bigg|\frac{\partial x(t,y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n \quad \Rightarrow \\ |
| − | \Rightarrow \quad V_t=\int\limits_{D_t} dx_t=\int\limits_{D_t} dx_1(t | + | \Rightarrow \quad V_t=\int\limits_{D_t} dx_t=\int\limits_{D_t} dx_1(t,y)\,dx_2(t,y)\,...\, dx_n(t,y)=\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n.\\ |
\end{gather*} | \end{gather*} | ||
\begin{gather*} | \begin{gather*} | ||
| − | \frac{dV_t}{dt}=\int\limits_{D_0} \frac{d}{dt}\bigg(\bigg|\frac{\partial x(t | + | \frac{dV_t}{dt}=\int\limits_{D_0} \frac{d}{dt}\bigg(\bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 2}\right\}=\\ |
| − | =\int\limits_{D_0} \bigg|\frac{\partial x(t | + | =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\Bigg(\frac{d}{dt}\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 1}\right\}=\\ |
| − | =\int\limits_{D_0} \bigg|\frac{\partial x(t | + | =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\Bigg(\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\\ |
| − | =\int\limits_{D_0} \bigg|\frac{\partial x(t | + | =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\bigg(\frac{\partial f}{\partial x}\bigg) \,dy_1\,dy_2\,...\, dy_n=\int\limits_{D_t} \tr\bigg(\frac{\partial f}{\partial x}\bigg) dx_t=\int\limits_{D_t} \div\, f\, dx_t. |
\end{gather*} | \end{gather*} | ||
| Строка 145: | Строка 164: | ||
'''Следствие.''' | '''Следствие.''' | ||
| − | Пусть задана [https://ru.wikipedia.org/wiki/Система_линейных_дифференциальных_уравнений система линейных дифференциальных уравнений]: | + | Пусть задана [https://ru.wikipedia.org/wiki/Система_линейных_дифференциальных_уравнений система линейных дифференциальных уравнений] с постоянными коэффициентами: |
\begin{gather*} | \begin{gather*} | ||
\frac{dx_i}{dt}=\sum\limits_{j=1}^n a_{ij}\,x_j. | \frac{dx_i}{dt}=\sum\limits_{j=1}^n a_{ij}\,x_j. | ||
| Строка 151: | Строка 170: | ||
Её также можно записать в матричном виде: | Её также можно записать в матричном виде: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \dot{x}=Ax=f(x), \quad { где } \quad A=\big(a_{ij} | + | \dot{x}=Ax=f(x), \quad { где } \quad A=\big(a_{ij}\big)\bigg|_{i,j=\overline{1,n}}. |
\end{gather*} | \end{gather*} | ||
Очевидно, что при таких условиях верно: | Очевидно, что при таких условиях верно: | ||
\begin{gather*} | \begin{gather*} | ||
| − | div\, | + | \div\,f=\tr A. |
\end{gather*} | \end{gather*} | ||
Тогда по ''Теореме Лиувилля'' имеем: | Тогда по ''Теореме Лиувилля'' имеем: | ||
\begin{gather*} | \begin{gather*} | ||
| − | \frac{d V_t}{dt}=\int\limits_{D_t} | + | \frac{d V_t}{dt}=\int\limits_{D_t} \tr A\, dx_t=\tr A \cdot\int\limits_{D_t} dx_t=\tr A \cdot V_t. |
\end{gather*} | \end{gather*} | ||
Таким образом, получили дифференциальное уравнение, решение которого [https://ru.wikipedia.org/wiki/Простейшие_дифференциальные_уравнения_первого_порядка элементарно находится]: | Таким образом, получили дифференциальное уравнение, решение которого [https://ru.wikipedia.org/wiki/Простейшие_дифференциальные_уравнения_первого_порядка элементарно находится]: | ||
\begin{gather*} | \begin{gather*} | ||
| − | V_t=V_0\, e^{ | + | V_t=V_0\, e^{(\tr A) \cdot t}. |
\end{gather*} | \end{gather*} | ||
Понятно, что с использованием свойств [https://ru.wikipedia.org/wiki/Экспонента экспоненты] можно заключить следующее: | Понятно, что с использованием свойств [https://ru.wikipedia.org/wiki/Экспонента экспоненты] можно заключить следующее: | ||
| − | * $$\quad | + | * $$\quad \tr A>0 \quad \Rightarrow \quad \text{траектории разбегаются.}$$ |
| − | * $$\quad | + | * $$\quad \tr A<0 \quad \Rightarrow \quad \text{траектории сближаются.}$$ |
| − | * $$\quad | + | * $$\quad \tr A=0 \quad \Rightarrow \quad \text{фазовый объём сохраняется.}$$ |
== Пример сохранения фазового объёма== | == Пример сохранения фазового объёма== | ||
| Строка 190: | Строка 209: | ||
\end{gather*} | \end{gather*} | ||
\begin{gather*} | \begin{gather*} | ||
| − | + | \tr (A)=0, \text{ то есть фазовый объём сохраняется.} | |
\end{gather*} | \end{gather*} | ||
| + | |||
[[Файл:Pred2.jpg|300px|thumb|right|Фазовое пространство системы из примера. Траектории являются замкнутыми кривыми.]] | [[Файл:Pred2.jpg|300px|thumb|right|Фазовое пространство системы из примера. Траектории являются замкнутыми кривыми.]] | ||
Показать сохранение фазового объёма можно и через [https://ru.wikipedia.org/wiki/Первый_интеграл первый интеграл] (или энергию системы): | Показать сохранение фазового объёма можно и через [https://ru.wikipedia.org/wiki/Первый_интеграл первый интеграл] (или энергию системы): | ||
| Строка 197: | Строка 217: | ||
\frac{dx_2}{dx_1}=-\frac{x_1}{x_2},\\ | \frac{dx_2}{dx_1}=-\frac{x_1}{x_2},\\ | ||
\int x_2 \, dx_2=-\int x_1 \, dx_1,\\ | \int x_2 \, dx_2=-\int x_1 \, dx_1,\\ | ||
| − | x_1^2+x_2^2= | + | x_1^2+x_2^2=\text{const},\\ |
| − | H(x_1,x_2)=x_1^2+x_2^2 | + | H(x_1,x_2)=x_1^2+x_2^2 \text{ — энергия системы.} |
\end{gather*} | \end{gather*} | ||
| − | Итак, если $$(x_1(t),x_2(t))$$ | + | Итак, если $$(x_1(t),x_2(t))-$$ решение системы, то функция $$H(x_1(t),x_2(t))$$ не зависит от $$t:$$ |
\begin{gather*} | \begin{gather*} | ||
\frac{d}{dt} H(x_1(t),x_2(t))=\frac{\partial H(x_1(t),x_2(t))}{\partial x_1}\cdot \frac{dx_1}{dt}+\frac{\partial H(x_1(t),x_2(t))}{\partial x_2}\cdot \frac{dx_2}{dt}=2x_1x_2+2x_2(-x_1)=0. | \frac{d}{dt} H(x_1(t),x_2(t))=\frac{\partial H(x_1(t),x_2(t))}{\partial x_1}\cdot \frac{dx_1}{dt}+\frac{\partial H(x_1(t),x_2(t))}{\partial x_2}\cdot \frac{dx_2}{dt}=2x_1x_2+2x_2(-x_1)=0. | ||
| Строка 206: | Строка 226: | ||
Фазовые кривые являются окружностями, поэтому фазовый объём сохраняется. | Фазовые кривые являются окружностями, поэтому фазовый объём сохраняется. | ||
== Список литературы == | == Список литературы == | ||
| − | |||
| − | |||
# Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023. | ||
Текущая версия на 15:17, 24 сентября 2023
Содержание
Определения
Определение 1.
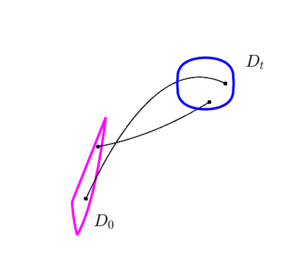
Пусть рассматривается система обыкновенных дифференциальных уравнений:
\begin{gather*}
\frac{dx_i}{dt}=f_i(x),\quad \text{где}\quad x=(x_1,...,x_n)\in \mathbb{R}^n,\\
f_i(x)\: — \text{ компоненты вектор-функции } f(x)=\big(f_1(x),...,f_n(x)\big);\\
x(0)=x_0\in D_0.
\end{gather*}
Введём обозначение для множества решений системы в фиксированный момент времени:
\begin{gather*}
D_t=\left\{\,x(t,x_0),\quad x_0\in D_0\right\}.
\end{gather*}
Фазовым объёмом множества $$D_t$$ называется выражение, определяемое по интегральной формуле:
\begin{equation}
%V_t=\underbrace{\int...\int}_{D_t} dx_1\,dx_2...dx_n.
\label{eq:0}
V_t=\int\limits_{D_t} dx_1 dx_2...dx_n.\\
\end{equation}
Определение 2.
Величина $$\dfrac{dV_t}{dt}$$ называется изменением фазового объёма.
Вспомогательные леммы
Лемма 1. (Уравнение в вариациях)
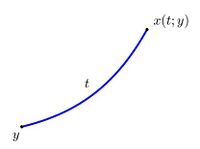
$$\quad$$ Пусть задана система обыкновенных дифференциальных уравнений: \begin{equation} \label{eq:1} \frac{dx}{dt}=f(x),\quad \text{где}\quad x=(x_1,...,x_n)\in \mathbb{R}^n \quad \text{и}\quad f(x)=\big(f_1(x),...,f_n(x)\big); \end{equation}
\begin{equation} \label{eq:2} x(0)=y, \quad y\in D_0. \end{equation}
Считаем, что $$x(t,y)$$ — решение системы \eqref{eq:1}-\eqref{eq:2} является дважды непрерывно дифференцируемой вектор-функцией в некоторой области, в которой и происходит рассмотрение леммы.
Запишем матрицу чувствительности начальных данных:
\begin{gather*} &\frac{\partial x(t,y)}{\partial y}=\bigg(\frac{\partial x_i}{\partial y_j}\bigg)_{i,j=\overline{1,n}}= \begin{pmatrix} \frac{\partial x_1}{\partial y_1}& \frac{\partial x_1}{\partial y_2}& ... & \frac{\partial x_1}{\partial y_n}\\ \frac{\partial x_2}{\partial y_1}& \frac{\partial x_2}{\partial y_2}& ... & \frac{\partial x_2}{\partial y_n}\\ ...&...&...&...\\ \frac{\partial x_n}{\partial y_1}& \frac{\partial x_n}{\partial y_2}& ... & \frac{\partial x_n}{\partial y_n}\\ \end{pmatrix}. \end{gather*} В этой матрице $$\dfrac{\partial x_i}{\partial y_j}$$ — скорость изменения координаты $$x_i$$ в зависимости от начального значения $$y_j.$$
Запишем ещё одну матрицу:
\begin{gather*} &\frac{\partial f}{\partial x}=\bigg(\frac{\partial f_i}{\partial x_j}\bigg)_{i,j=\overline{1,n}}= \begin{pmatrix} \frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& ... & \frac{\partial f_1}{\partial x_n}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& ... & \frac{\partial f_2}{\partial x_n}\\ ...&...&...&...\\ \frac{\partial f_n}{\partial x_1}& \frac{\partial f_n}{\partial x_2}& ... & \frac{\partial f_n}{\partial x_n}\\ \end{pmatrix}. \end{gather*}
Тогда лемма утверждает, что справедливо матричное равенство (уравнение в вариациях): \begin{gather*} \frac{d}{dt}\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)=\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg). \end{gather*} Доказательство.
Распишем покомпонентно систему \eqref{eq:1}: \begin{gather*} \frac{dx_i(t,y)}{dt}=f_i\big(x(t,y)\big) \quad \bigg| \cdot \frac{\partial}{\partial y_j}\\ \frac{\partial}{\partial y_j}\bigg(\frac{dx_i(t,y)}{dt}\bigg)=\frac{\partial}{\partial y_j}\Big(f_i\big(x(t,y)\big)\Big).\\ \end{gather*} Переставим операции местами, в силу достаточной гладкости функции: \begin{gather*} \frac{d}{dt}\bigg(\frac{\partial x_i(t,y)}{\partial y_j}\bigg)=\frac{\partial}{\partial y_j}\Big(f_i\big(x(t,y)\big)\Big)=\\ =\sum\limits_{s=1}^n \frac{\partial f_i}{\partial x_s} \cdot \frac{\partial x_s}{\partial y_j}=\bigg(\frac{\partial f_i}{\partial x_1},...,\frac{\partial f_i}{\partial x_n}\bigg)\cdot\bigg(\frac{\partial x_1}{\partial y_j},...,\frac{\partial x_n}{\partial y_j}\bigg)^T=\frac{\partial f_i}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y_j}\bigg). \end{gather*} Таким образом, получили: \begin{gather*} \frac{d}{dt}\bigg(\frac{\partial x_i(t,y)}{\partial y_j}\bigg)=\frac{\partial f_i}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y_j}\bigg), \quad \forall i,j=\overline{1,n}. \end{gather*} Получили то, что мы и хотели доказать.
$$\blacksquare$$
Лемма 2. (Лиувилля, о дифференцировании определителя)
$$\quad$$ Пусть задана матрица $$A(t)=\big(a_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}.$$
Напомним, что $$\tr A=\sum\limits_{i=1}^n a_{ii}$$ — след матрицы $$A.$$
Тогда справедливо следующее равенство: \begin{gather*} \frac{d}{dt}|A(t)|=|A(t)|\cdot \tr\big(A^{'}(t)A^{-1}(t)\big), \text{ где } A^{'}(t)=\big(a^{'}_{ij}(t)\big)\bigg|_{i,j=\overline{1,n}}=\bigg(\frac{d a_{ij}(t)}{dt}\bigg)\bigg|_{i,j=\overline{1,n}}. \end{gather*}
Доказательство.
По формуле Тейлора имеем: \begin{gather*} a_{ij}(t+\Delta t)=a_{ij}(t)+a^{'}_{ij}(t)\Delta t+\bar{o}(\Delta t).\\ |A(t+\Delta t)|=|A(t)+A^{'}(t)\Delta t+\bar{o}(\Delta t)|=\bigg|\big(E+A^{'}(t)A^{-1}(t)\Delta t+\bar{o}(\Delta t)\big)A(t)\bigg|=\\ =\big|A(t)\big|\cdot\big|E+A^{'}(t)A^{-1}(t)\Delta t+\bar{o}(\Delta t)\big|. \end{gather*}
\begin{gather*} \big|E+\underbrace{A^{'}(t)A^{-1}(t)}_{B(t)=\big(b_{ij}(t)\big)}\Delta t+\bar{o}(\Delta t)\big|= \begin{vmatrix} 1+b_{11}\Delta t+\bar{o}(\Delta t)& b_{12}\Delta t+\bar{o}(\Delta t)& ... & b_{1n}\Delta t+\bar{o}(\Delta t)\\ b_{21}\Delta t+\bar{o}(\Delta t)& 1+b_{22}\Delta t+\bar{o}(\Delta t)& ... & b_{2n}\Delta t+\bar{o}(\Delta t)\\ ...&...&...&...\\ b_{n1}\Delta t+\bar{o}(\Delta t)& b_{n2}\Delta t+\bar{o}(\Delta t)& ... & 1+b_{nn}\Delta t+\bar{o}(\Delta t)\\ \end{vmatrix}. \end{gather*} Так как определитель матрицы представляет собой сумму всевозможных произведений элементов матрицы, взятых ровно по одному из каждой строки и из каждого столбца, получаем: \begin{gather*} \big|E+B(t)\Delta t+\bar{o}(\Delta t)\big|=1+\Delta t\cdot \tr\big(A^{'}(t)A^{-1}(t)\big)+\bar{o}(\Delta t).\\ \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=\frac{\big|A(t)\big|\cdot \big(1+\Delta t \cdot \tr\big(A^{'}(t)A^{-1}(t)\big)+\bar{o}(\Delta t)-1\big)}{\Delta t}=|A(t)|\cdot \big(\tr(A^{'}(t)A^{-1}(t))+\bar{o}(1)\big).\\ \frac{d}{dt}|A(t)|=\lim\limits_{\Delta t\to 0} \frac{\big|A(t+\Delta t)\big|-\big|A(t)\big|}{\Delta t}=|A(t)|\cdot \tr\big(A^{'}(t)A^{-1}(t)\big). \end{gather*} $$\blacksquare$$
Теорема Лиувилля об изменении фазового объёма
Теорема.
$$\quad$$ Пусть задана система \eqref{eq:1} с начальным условием \eqref{eq:2}.
Также заданы множества решений системы в фиксированные моменты времени: \begin{gather*} D_t=\left\{\,x(t,y),\quad y\in D_0\right\}. \end{gather*} Определим по формуле \eqref{eq:0} соответствующие фазовые объёмы $$V_t$$ для множеств $$D_t.$$ В частности, фазовый объём множества $$D_0$$ обозначим через $$V_0.$$
Тогда верна следующая формула для нахождения изменения фазового объёма: \begin{gather*} \frac{d V_t}{dt}=\int\limits_{D_t} \div\, f\, dx_t,\quad \text{ где }\quad d x_t=dx_1\,dx_2\,...\,dx_n. \end{gather*} Напомним определение дивиргенции векторного поля $$f:$$ \begin{gather*} \div\, f=\sum\limits_{i=1}^n \frac{\partial f_i}{\partial x_i}(x). \end{gather*}
Доказательство.
\begin{gather*} dx_t=dx_1(t,y)\,dx_2(t,y)\,...\, dx_n(t,y)=\bigg|\frac{\partial x(t,y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n \quad \Rightarrow \\ \Rightarrow \quad V_t=\int\limits_{D_t} dx_t=\int\limits_{D_t} dx_1(t,y)\,dx_2(t,y)\,...\, dx_n(t,y)=\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg| \,dy_1\,dy_2\,...\, dy_n.\\ \end{gather*}
\begin{gather*} \frac{dV_t}{dt}=\int\limits_{D_0} \frac{d}{dt}\bigg(\bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 2}\right\}=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\Bigg(\frac{d}{dt}\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\left\{\text{Лемма 1}\right\}=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\Bigg(\frac{\partial f}{\partial x}\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)\cdot\bigg(\frac{\partial x(t,y)}{\partial y}\bigg)^{-1}\Bigg) \,dy_1\,dy_2\,...\, dy_n=\\ =\int\limits_{D_0} \bigg|\frac{\partial x(t,y)}{\partial y}\bigg|\cdot \tr\bigg(\frac{\partial f}{\partial x}\bigg) \,dy_1\,dy_2\,...\, dy_n=\int\limits_{D_t} \tr\bigg(\frac{\partial f}{\partial x}\bigg) dx_t=\int\limits_{D_t} \div\, f\, dx_t. \end{gather*}
$$\blacksquare$$
Следствие теоремы Лиувилля для линейных систем
Следствие.
Пусть задана система линейных дифференциальных уравнений с постоянными коэффициентами: \begin{gather*} \frac{dx_i}{dt}=\sum\limits_{j=1}^n a_{ij}\,x_j. \end{gather*} Её также можно записать в матричном виде: \begin{gather*} \dot{x}=Ax=f(x), \quad { где } \quad A=\big(a_{ij}\big)\bigg|_{i,j=\overline{1,n}}. \end{gather*} Очевидно, что при таких условиях верно: \begin{gather*} \div\,f=\tr A. \end{gather*}
Тогда по Теореме Лиувилля имеем: \begin{gather*} \frac{d V_t}{dt}=\int\limits_{D_t} \tr A\, dx_t=\tr A \cdot\int\limits_{D_t} dx_t=\tr A \cdot V_t. \end{gather*} Таким образом, получили дифференциальное уравнение, решение которого элементарно находится: \begin{gather*} V_t=V_0\, e^{(\tr A) \cdot t}. \end{gather*} Понятно, что с использованием свойств экспоненты можно заключить следующее:
- $$\quad \tr A>0 \quad \Rightarrow \quad \text{траектории разбегаются.}$$
- $$\quad \tr A<0 \quad \Rightarrow \quad \text{траектории сближаются.}$$
- $$\quad \tr A=0 \quad \Rightarrow \quad \text{фазовый объём сохраняется.}$$
Пример сохранения фазового объёма
Пример.
Пусть задана линейная система ОДУ:
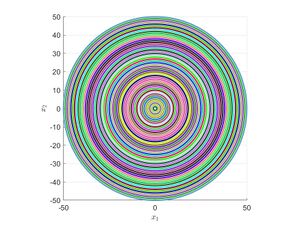
\begin{gather*} \begin{cases} \dot{x}_1=x_2,\\ \dot{x}_2=-x_1. \end{cases} \end{gather*} Тогда матрица $$A$$ системы выписывается элементарно: \begin{gather*} A=\begin{pmatrix} 0 & 1\\ -1 & 0 \end{pmatrix}. \end{gather*} \begin{gather*} \tr (A)=0, \text{ то есть фазовый объём сохраняется.} \end{gather*}
Показать сохранение фазового объёма можно и через первый интеграл (или энергию системы): \begin{gather*} \frac{dx_2}{dx_1}=-\frac{x_1}{x_2},\\ \int x_2 \, dx_2=-\int x_1 \, dx_1,\\ x_1^2+x_2^2=\text{const},\\ H(x_1,x_2)=x_1^2+x_2^2 \text{ — энергия системы.} \end{gather*} Итак, если $$(x_1(t),x_2(t))-$$ решение системы, то функция $$H(x_1(t),x_2(t))$$ не зависит от $$t:$$ \begin{gather*} \frac{d}{dt} H(x_1(t),x_2(t))=\frac{\partial H(x_1(t),x_2(t))}{\partial x_1}\cdot \frac{dx_1}{dt}+\frac{\partial H(x_1(t),x_2(t))}{\partial x_2}\cdot \frac{dx_2}{dt}=2x_1x_2+2x_2(-x_1)=0. \end{gather*} Фазовые кривые являются окружностями, поэтому фазовый объём сохраняется.
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.