Выпуклое множество и его свойства
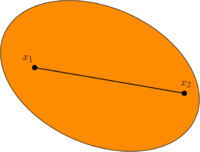
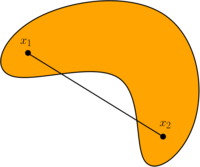
Выпуклое множество в линейном пространстве $$X$$ — множество, содержащее любые две его точки вместе с отрезком, соединяющим их. Выпуклые множества играют важную роль во многих оптимизационных задачах.
Содержание
Определения выпуклого множества, суммы множеств и произведения множества на число
1. Множество $$A$$ называется выпуклым, если для любых двух точек $$x_1,x_2\in A$$ выполняется \begin{gather*} [x_1,x_2]\subset A, \text{ т.е. } \alpha x_1+(1-\alpha x_2)\in A~~\forall\alpha\in[0,1]. \end{gather*}
2. Пусть $$A,B\subset X$$ и $$\alpha\in\mathbb{R}$$. Введем в рассмотрение множества \begin{gather*} A+B=\{x\in X\mid ~x=a+b,~a\in A,~b\in B\},\\ \alpha A=\{x\in X\mid x=\alpha a, ~a\in A\}. \end{gather*}
Выпуклая комбинация точек и выпуклая оболочка множества
Сумма $$\sum\limits_{i=1}^k\alpha_i x_i$$ называется выпуклой комбинацией точек $$x_1,\ldots,x_k$$, если $$\alpha_i\geq0,~i=1,\ldots,k,~\sum\limits_{i=1}^k\alpha_i=1$$.
Выпуклой оболочкой множества $$A$$ называется множество, обозначаемое $$\operatorname{conv}(A)$$: \begin{gather*} \operatorname{conv}(A)=\bigcap\{B\subseteq X\mid A\subseteq B,~B\text{ - выпукло}\}. \end{gather*}
Примеры выпуклых множеств
1. Все пространство $$X$$.
2. Множество, состоящее из одной точки $$\{x\}$$.
3. Пустое множество $$\emptyset$$.
4. Симплекс (n-симплекс, где n - размерность симплекса) — выпуклая оболочка $$n+1$$ афинно независимых точек афинного пространства. То есть эти точки, называемые вершинами симплекса, не лежат на гиперплоскости размерности $$n-1$$.
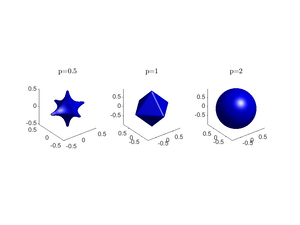
5. Единичный шар — множество $$B_1(0)=\{x\in X\mid\rho(x,0)\leqslant1\}$$ в пространстве $$X$$ с метрикой $$\rho(\cdot,\cdot)$$.
Однако с единичным шаром не все так просто. В общем случае можно утверждать о выпуклости единичного шара, если в пространстве $$X$$ существует норма $$\|\cdot\|:~\rho(x,y)=\|x-y\|$$.
Для примера рассмотрим пространство $$\mathbb{R}^n$$ и метрику $$\rho_p(x,y)=\sqrt[p]{|x_1-y_1|^p+|x_2-y_2|^p+\ldots+|x_n-y_n|^p},~p>0$$. Можно показать, что при $$p\geqslant1$$ данная метрика согласуется с нормой $$\|\cdot\|_p$$. Если же $$p\in(0,1)$$, то единичный шар перестает быть выпуклым.
Свойства выпуклых множеств
- Пересечение любого числа выпуклых множеств $$A_\sigma\subset X,~\sigma\in\Sigma$$ является выпуклым множеством.
Доказательство:
Возьмем произвольные точки $$x, y \in \bigcap\limits_{\sigma \in \Sigma} A_\sigma$$. Каждое из множеств $$A_\sigma$$ является выпуклым. Поэтому $$[x, y] \subset A_\sigma$$ для любого $$\sigma \in \Sigma$$. Отсюда $$[x, y] \subset \bigcap\limits_{a \in \Sigma} A_\sigma$$, что по определению означает выпуклость пересечения множеств $$\bigcap\limits_{\sigma \in \Sigma} A_\sigma$$. $$~~\blacksquare$$
- Пусть $$A_1,\ldots,A_n$$ — выпуклые подмножества $$X,~\alpha_1,\ldots,\alpha_n\in\mathbb{R}$$. Тогда множество $$\sum\limits_{i=1}^n\alpha_i A_i$$ выпукло.
Доказательство:
Возьмем произвольные точки $$x, y \in \sum\limits_{i=1}^n \alpha_i A_i$$. По определению существуют $$x_1, y_1 \in A_1, \ldots, x_n, y_n \in A_n$$ такие, что \begin{gather*} x=\sum\limits_{i=1}^n \alpha_i x_i, \quad y=\sum\limits_{i=1}^n \alpha_i y_i. \end{gather*} Из выпуклости множеств $$A_i$$ следует, что для любых $$\alpha, \beta \geq 0$$, $$\alpha+\beta=1$$, имеет место $$\alpha x_i+\beta y_i \in A_i$$ и, значит, $$\alpha x+\beta y=\sum\limits_{i=1}^n \alpha_i\left(\alpha x_i+\beta y_i\right) \in \sum\limits_{i=1}^n \alpha_i A_i$$, откуда вытекает выпуклость множества $$\sum\limits_{i=1}^n \alpha_i A_i$$.
Из определения операции суммы множеств и произведения множества на число непосредственно вытекает включение \begin{gather*} (\alpha+\beta) A \subset \alpha A+\beta A \end{gather*} справедливое для произвольного множества $$A$$ и чисел $$\alpha, \beta$$. $$~~\blacksquare$$
- Пусть $$A$$ — выпуклое множество. Тогда для любых $$\alpha\geq0,~\beta\geq0$$ справедлива формула
\begin{gather*} (\alpha+\beta)A=\alpha A+\beta A. \end{gather*}
Доказательство:
В силу сказанного выше достаточно доказать включение $$\alpha A+\beta A\subset(\alpha+\beta)A.$$ Если $$\alpha+\beta=0$$, то $$\alpha=\beta=0$$ и, значит, это включение очевидно. Рассмотрим случай $$\alpha+\beta>0$$. Пусть $$\xi\in\alpha A+\beta A$$. Тогда $$\xi=\alpha x_1+\beta x_2$$ для некоторых $$x_1,x_2\in A$$, откуда в силу выпуклости $$A$$ имеем \begin{gather*} \xi=(\alpha+\beta)\left(\dfrac{\alpha}{\alpha+\beta}x_1+\dfrac{\beta}{\alpha+\beta}x_2\right)\in(\alpha+\beta)A, \end{gather*} что завершает доказательство нужного включения. $$~~\blacksquare$$
- Выпуклое множество $$A$$ содержит любую выпуклую комбинацию своих точек.
Доказательство:
Необходимо показать, что для любого $$n\geq2$$ из того, что \begin{gather*} x=\sum\limits_{i=1}^n\alpha_i x_i,\quad x_i\in A,~\alpha_i\geq0,\quad\sum\limits_{i=1}^n\alpha_i=1, \end{gather*} следует, что $$x\in A$$.
Докажем по индукции. При $$n=2$$ искомое утверждение следует из определения выпуклого множества. Пусть искомое утверждение доказано для $$n=r$$. Докажем его для $$n=r+1$$.
Не ограничивая общности рассуждений, будем считать, что $$\sum\limits_{i=1}^r\alpha_i>0.$$ Тогда \begin{gather*} \sum\limits_{i=1}^{r+1}\alpha_i x_i=\sum\limits_{i=1}^r\alpha_i\left(\sum\limits_{i=1}^r\dfrac{\alpha_i}{\sum\limits_{i=1}^r\alpha_i}x_i\right)+\alpha_{r+1}x_{r+1}=\tilde{\alpha}\tilde{x}+\alpha_{r+1}x_{r+1}\in A \end{gather*} в силу выпуклости множества $$A$$. Здесь $$\tilde{x}\in A$$ в силу выпуклости $$A$$ и предположения индукции, а $$\tilde{\alpha}=\sum\limits_{i=1}^r\alpha_i$$, следовательно, $$\tilde{\alpha}+\alpha_{r+1}=1$$. $$~~\blacksquare$$
Список литературы
1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004.