Опорная функция множества

Одним из удобных инструментов для работы с выпуклыми множествами является математический аппарат опорных функций. Будем рассматривать евклидово пространство $$\mathbb{R}^n$$, хотя опорные функции могут быть определены и для более общего класса линейных пространств.

Определение и интерпретация

Опорная функция множества

Пусть $$Z \subseteq \mathbb{R}^n$$, тогда опорной функцией множества $$Z$$ будем называть функцию $$\rho(\cdot \mid Z) \colon\ \mathbb{R}^n \mapsto \mathbb{R} \cup \{ \pm \infty \}$$, такую что: \[ \begin{cases} \rho (l \mid Z) = \sup \{ \left< l, z \right> \mid z \in Z \}, & Z \neq \varnothing, \\ \rho (l \mid Z) = -\infty, & Z = \varnothing. \end{cases} \]

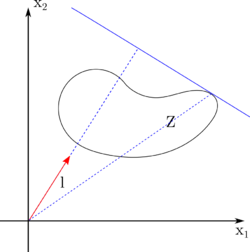
Опорная функция имеет достаточно простую геометрическую интерпретацию. Рассмотрим множество $$Z$$ на плоскости и некоторое направление $$l$$. Для простоты положим $$\| l \| = 1$$. Тогда опорной функцией множества $$Z$$ в направлении $$l$$ будет расстояние (со знаком!) от начала координат до самой дальней гиперплоскости с нормалью $$l$$, которая касается (в нестрогом смысле) множества. То есть другими словами мы начинаем отодвигать гиперплоскость с нормалью $$l$$ в направлении $$l$$ до тех пор, пока дальше уже не будет множества. И в этот момент считаем скалярное произведение, что равно произведению длины $$l$$ и расстоянию до полученной гиперплоскости. Если в данном направлении «нет множества», но оно есть в противоположном направлении, то значение функции будет со знаком «минус». Множество, на котором достигается супремум в определении, называется опорным множеством. В случае, когда множество является компактом, супремум можно заменить на максимум, потому что он достигается. Если же множество к тому же является строго выпуклым, то максимум достигается в единственной точке, которую называют опорным вектором.

Свойства

Свойства опорной функции как функции от $$l$$:

1. Выпуклость: $$\rho\bigl(\alpha l_1 + (1 - \alpha)l_2 \mid Z\bigr) \leqslant \alpha \rho(l_1 \mid Z) + (1 - \alpha) \rho(l_2 \mid Z), \quad \forall \alpha \in [0, 1], \quad \forall l_1, l_2 \in \mathbb{R}^n$$.
2. Положительная однородность: $$\rho(\alpha l \mid Z) = \alpha \rho(l \mid Z), \quad \forall \alpha > 0, \quad \forall l \in \mathbb{R}^n$$.
3. Если $$Z$$ — ограниченное множество, то опорная функция принимает только конечные значения из $$\mathbb{R}$$.
4. Ключевое свойство, делающее аппарат опорных функций крайне удобным: для любой выпуклой положительно однородной функции, принимающей конечные значения, существует единственный выпуклый компакт, для которого эта функция является опорной.
5. Опорная функция множества $$Z$$ является сопряженной по Фенхелю к индикаторной функции множества:

\[ \delta_Z(z) = \begin{cases} 0, & z \in Z, \\ +\infty, & z \notin Z. \end{cases} \]

Свойства как функции от $$Z$$:

1. Неотрицательная однородность: $$\rho (l \mid \alpha Z) = \alpha \rho (l \mid Z), \quad \forall Z \neq \varnothing$$.
2. Аддитивность $$\rho(l \mid Z_1 + Z_2) = \rho(l \mid Z_1) + \rho(l \mid Z_2), \quad \forall Z_1, Z_2 \neq \varnothing$$, где сумма понимается в смысле Минковского. В частности, если $$Z_2 = \{z_2\}$$ — множество из одной точки, то $$\rho(l \mid Z_1 + Z_2) = \rho(l \mid Z_1) + \left< l, z_2 \right>$$
3. Опорная функция любого замкнутого множества равно опорной функции его выпуклой оболочки.
4. Опорная функция объединения множеств равна максимуму из опорных функций множеств: $$\rho(l \mid Z_1 \cup Z_2) = \rho(l \mid Z_1) \vee \rho(l \mid Z_2), \quad \forall Z_1, Z_2 \neq \varnothing$$
5. Опорная функция пересечения множеств равна наибольшей выпуклой функции, не превосходящей минимум из опорных функций множеств: $$\rho(l \mid Z_1 \cap Z_2) = \mathrm{conv} \bigl( \rho(l \mid Z_1) \wedge \rho(l \mid Z_2)\bigr), \quad \forall Z_1, Z_2 \neq \varnothing$$

Отделимость и расстояние Хаусдорфа

Множества $$A, B \in \mathbb{R}^n$$ называются (строго) отделимыми, если существует гиперплоскость, их (строго) отделяющая: $$\exists l \in \mathbb{R}^n \colon\ \forall x \in A, y \in B\ \left< l, x \right> \leqslant (<) \left<l, y\right>$$. В терминах опорных функций это означает, что существует $$l \in \mathbb{R}^n$$, для которого: \[ \rho(l \mid A) \leqslant (<) \rho(-l \mid B). \]

Расстояние Хаусдорфа между двумя выпуклыми компактами выражается через опорные функции следующим образом: \[ d_H(A, B) = \max\limits_{\| l \| \leqslant 1} \left\{ -\rho(-l \mid A) - \rho(l \mid B) \right\}. \] Здесь мы пишем $$\leqslant 1$$, чтобы корректно учесть случай, когда одно множество вложено в другое. Тогда если максимизировать по всем $$l$$ из единичной сферы, может получиться отрицательное число, а расстояние всегда неотрицательно. Поэтому мы рассматриваем $$l$$ из шара, а не из сферы. В принципе, достаточно рассматривать $$l$$ из сферы в объединении со случаем $$l = 0$$.

Опорные функции некоторых множеств

Точка

Пусть $$z \in \mathbb{R}^n$$. Супремум в определении вырождается в скалярное произведение и имеем: \[ \rho (l \mid z) = \left<l, z\right>. \]

Многогранник

Пусть $$\tilde Z = \{p_1,\ldots,p_m\}$$, рассмотрим многогранник $$Z = \mathrm{conv}\,\tilde Z$$. Так как опорная функция множества совпадает с опорной функцией его выпуклой оболочки, то: \[ \rho(l \mid Z) = \max_{i=\overline{1,m}} \left< l, p_i \right>. \] Опорным множеством будет та грань многогранника, которая содержит все точки, на которых достигается максимум.

Невырожденный эллипсоид

Пусть $$Z = \mathcal{E}(p, P)$$ — эллипсоид с центром в точке $$p$$ и невырожденной симметричной положительно определенной матрицей конфигурации $$P$$. По определению эллипсоида $$\mathcal{E}(p, P) = \{ z \in \mathbb{R}^n \mid \left< z - p, P^{-1}(z - p) \right> \leqslant 1 \}$$. Для начала заметим, что $$\mathcal{E}(p, P) = p + \mathcal{E}(0, P)$$, откуда $$\rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \rho \bigl(l \mid \mathcal{E}(0, P)\bigr)$$. Для нахождении опорной функции поставим задачу оптимизации: \[ \begin{cases} \left<l, z\right> \rightarrow \max, \\ \left<z, P^{-1}z\right> \leqslant 1. \end{cases} \] Так как эллипсоид является выпуклым компактом, то максимум в определении достигается в единственной точке на границе эллипсоида, поэтому задача сводится к более простой: \[ \begin{cases} \left<l, z\right> \rightarrow \max, \\ \left<z, P^{-1}z\right> = 1. \end{cases} \] Для решения применим метод множителей Лагранжа: \[ L(z) = \left<l, z\right> - \frac\lambda2 \left<z, P^{-1}z\right>,\\ L'(z^*) = 0 = l - \lambda P^{-1}z^*. \] Отсюда выражаем $$z^*$$ через $$\lambda$$ и $$l$$ и подставляем в ограничение: \[ z^* = \frac1\lambda P l, \\ \left<z^*, P^{-1}z^*\right> = 1 = \left<\frac1\lambda P l, \frac1\lambda l\right> = \frac1{\lambda^2} \left< Pl, l \right>, \\ z^* = \frac{Pl}{\sqrt{\left< l, Pl\right>}}. \] Получили опорный вектор для направления $$l$$. Подставляя его в скалярное произведение, которое мы максимизируем, получаем: \[ \rho\bigl(l \mid \mathcal{E}(0, P)\bigr) = \left<l, z^*\right> = \frac{\left< l, Pl\right>}{\sqrt{\left< l, Pl\right>}} = \sqrt{\left< l, Pl\right>}. \] Окончательно для произвольного эллипсоида: \[ \rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \sqrt{\left< l, Pl\right>}, \\ z^* = p + \frac{Pl}{\sqrt{\left< l, Pl\right>}}. \]