Приложения преобразования Лапласа
Приведем основные формулы и свойтсва, используемые для решения дифференциальных уравнений и вычисления матричных экспоненциалов с помощью преобразования Лапласа:
Прямое и обратное преобразование Лапласа некоторых функций:
- $$x(t) \supset \frac{1}{p}$$
- $$x(t)t^n \supset \frac{n!}{p^{n+1}}$$
- $$x(t)t^{\alpha}e^{\beta t} \supset \frac{n!}{(p-\beta)^{n+1}}, \beta \in \mathbb{C}$$
- $$x(t)t^{\alpha}\cos{\omega t} \supset \frac{\varGamma (\alpha + 1)}{2}\left(\frac{1}{(p-\omega i)^{\alpha+1}} + \frac{1}{(p+\omega i)^{\alpha+1}} \right)$$
- $$x(t)t^{\alpha}\sin{\omega t} \supset \frac{\varGamma (\alpha + 1)}{2}\left(\frac{1}{(p-\omega i)^{\alpha+1}} - \frac{1}{(p+\omega i)^{\alpha+1}} \right)$$
- $$x(t)\sin{\omega t} \supset \frac{\omega}{p^2 + \omega^2}$$
- $$x(t)\cos{\omega t} \supset \frac{p}{p^2 + \omega^2}$$
- $$x(t)e^{\beta t}\sin{\omega t} \supset \frac{\omega}{(p-\beta)^2 + \omega^2}$$
- $$x(t)e^{\beta t}\cos{\omega t} \supset \frac{p-\beta}{(p-\beta)^2 + \omega^2}$$
- $$x(t)e^{\beta t} \supset \frac{1}{p-\beta}$$
- $$x(t)\operatorname{sh}{\omega t} \supset \frac{\omega}{p^2 - \omega^2}$$
- $$x(t)\operatorname{ch}{\omega t} \supset \frac{p}{p^2 - \omega^2}$$
- $$x(t)e^{\beta t}\operatorname{sh}{\omega t} \supset \frac{\omega}{(p-\beta)^2 - \omega^2}$$
- $$x(t)e^{\beta t}\operatorname{ch}{\omega t} \supset \frac{p-\beta}{(p-\beta)^2 - \omega^2}$$,
$$\text{где } x(t)$$ - функция Хевисайда.
Свойства:
- $$f(at) \supset \frac{1}{a}F(\frac{p}{a}) \, , \, a > 0$$
- $$\frac{1}{b}\,f(\frac{t}{b}) \supset F(pb) \, , \, b > 0 \,;\, b=\frac{1}{a}$$
- $$x(t-a)f(t-a) \supset e^{-ap}F(p)$$
- $$x(t)f(t+a) \supset e^{ap}\left(F(p)-\int\limits_0^a f(t)e^{-pt} dt \right) $$
- $$x(t)e^{\beta t} \supset F(p+\beta)$$
Дифференцируемость:
- $$f^{(k)}(t) \supset p^{k}F(p) - p^0f^{(k-1)}(0) - pf^{(k-2)}(0) - \ldots - p^{k-1}f(0)$$
- $$x(t)(-t)^k \supset F^{(k)}(p)$$
Интегрируемость:
- $$\int\limits_0^t f(\tau) d\tau \supset \frac{F(p)}{p}$$
- $$\frac{f(t)}{t} \supset \int\limits_0^{+\infty}F(z) dz$$
Примеры:
Нахождение фундаментальной матрицы:
\(
\dot X = AX\, , \, X \in \mathbb{R}^{n}, \,A \in \mathbb{R}^{n \times n} \)
X(t) - фундаментальная матрица, если: \(\left\{ \begin{array}{rcl}
\frac{dX}{dt}=AX \\
X(0) = I
\end{array}
\right.
\)
Пусть $$X(t) \leftrightarrow Y(p)$$, тогда преобразуем систему по Лапласу $$\Rightarrow$$
$$\Rightarrow PY-I=AY \Rightarrow Y = (PI-A)^{-1}$$
Пример:
\(\left\{ \begin{array}{}
\dot X = \begin{pmatrix}
1 & 2 \\
-3 & 1
\end{pmatrix}X \\
X(0) = I
\end{array}
\right.,\quad Y = \begin{pmatrix}
p-1 & -2 \\
3 & p-1
\end{pmatrix}^{-1} = \frac{1}{(p-1)^2+6}\begin{pmatrix}
p-1 & 2 \\
-3 & p-1
\end{pmatrix}
\)
От каждого элемента матрицы Y нужно вычислить преобразование Лапласа, и получим:
\(
X(t) = \begin{pmatrix}
e^t\cos{\sqrt{6}t} & \frac{2}{\sqrt{6}}e^t\sin{\sqrt{6}t} \\
-\frac{3}{\sqrt{6}}e^t\sin{\sqrt{6}t} & e^t\cos{\sqrt{6}t}
\end{pmatrix}
\)
Решение дифференциальных уравнений:
Неоднородное дифференциальное уравнение:
\( \left\{ \begin{array}{} x''(t) + x(t) = 2\cos{t} \\ x(0) = 0, \, x'(0) = -1 \end{array} \right. \\ x(t) \supset X(p) \Rightarrow p^2X + 1 + X = 2\frac{p}{p^2+1} \\ X(p^2+1) = \frac{2p}{p^2+1}-1 \\ X(p) = \frac{2p}{(p^2+1)^2} - \frac{1}{(p^2+1)} \subset x(t) = t\sin{t} - \sin{t} \)
Система линейных неоднородных уравнений:
\( \left\{ \begin{array}{} x'(t) -y'(t) - 2x +2y = 1-2t \\ x''(t) + 2y'(t) + x = 0\\ x(0) = y(0) = x'(0) = 0 \end{array} \right. \\ \text{Преобразуем оба уравнение по Лапласу:} \\ \left\{ \begin{array}{} pX - pY -2(X-Y) = \frac{1}{p}-\frac{2}{p^2} \\ p^2X + 2pY + X = 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{} X-Y = \frac{1}{p^2} \\ p^2X + 2pY + X = 0 \end{array} \right. \\ p^2(Y+\frac{1}{p^2}) + 2pY + Y + \frac{1}{p^2} = 0 \\ Y(p) = -\frac{1}{(p+1)^2} - \frac{1}{p^2(p+1)} = -\frac{2}{(p+1)^2} - \frac{1}{p^2} + \frac{2}{p} - \frac{2}{p+1} \\ X(p) = -\frac{2}{(p+1)^2} + \frac{2}{p} - \frac{2}{p+1} \\ \text{И получим: } \\ X(p) \subset x(t) = -2te^{-t} + 2 - 2e^{-t} \\ Y(p) \subset y(t) = -2te^{-t} - t + 2 - 2e^{-t} \)
Расчеты в электрических цепях:
Пусть силе тока соответствует изображение \(i(t) \supset I(p)\).
- Мгновенные значения напряжения и тока связаны законом Ома: \(u(t)=Ri(t) \Rightarrow \)
Изображение напряжения выглядит следующим образом: \(u(t) \supset U(t) = RI(p).\)
- Мгновенные значения напряжения и тока индуктивности связаны как: \(u_L(t) = L\frac{di(t)}{dt} \Rightarrow \)
Воспользовавшись свойством дифференцируемости, найдем изображение напряжения: \(u_L(t) \supset U_L(t) = pLI(p) - Li(0).\)
- Мгновенные значения напряжения и тока емкости связаны как: \(u_С(t) = \frac1C\int_0^t i(\tau)d\tau \Rightarrow \)
Воспользовавшись свойством интегрируемости, найдем изображение напряжения: \(u_C(t) \supset U_C(t) = \frac{I}{Cp}.\)
ЭДС:
- постоянный ток: \(e(t) = e_0 \supset E(p) = \frac{e_0}{p} \)
- переменный ток: \(e(t) = e_0\sin\omega t \supset E(p) = \frac{e_0 \omega}{p^2+\omega^2} \)
Пример:
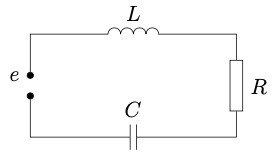
Пусть имеется цепь, показанная на схеме справа, и известно, что \(i(0) = 0.\)
Тогда по второму закону Киргофа имеем:
\[L\frac{di(t)}{dt} + Ri(t) + \frac1C\int_0^t i(\tau)d\tau = e(t).\]
Применяя к каждому слагаемому соответствующее преобразование, получим:
\[pLI(p) + RI(p) + \frac{I(p)}{Cp} = E(p).\]
\(Z(p) = pL + R + \frac{1}{Cp} -\) импеданс
\(Y(p) = \frac{1}{Z(p)} -\) адмитанс