Топологически орбитально эквивалентные системы

Рассмотрим две динамические системы с непрерывным временем \begin{align}\label{sys1} \dot{u} = g(u), \quad u \in \mathbb{R}^n,\\ \label{sys2} \dot{v} = f(v), \quad v \in \mathbb{R}^n, \end{align} где $$g(u) = (g_1(u), g_2(u), \dots, g_n(u)), f(v) = (f_1(v), f_2(v), \dots, f_n(v)).$$

Пусть функции $$f(\cdot)$$ и $$g(\cdot)$$ связаны соотношением \begin{equation} \label{func_dep} g(u) = \mu(u)f(u), \forall u \in U \subset \mathbb{R}^n, \end{equation} где $$\mu(\cdot)$$ — гладкая скалярная положительная для всех $$u \in U$$ функция.

Системы \eqref{sys1} и \eqref{sys2}, правые части которых связаны соотношением \eqref{func_dep}, называются орбитально эквивалентными в области $$U$$.

Свойства орбитально эквивалентных систем

Утверждение. Орбитально эквивалентные системы в области $$U$$ являются топологически эквивалентными в этой области.

Доказательство. Особые точки систем \eqref{sys1} и \eqref{sys2} являются корнями уравнений: \begin{align*} f(u) = 0,\\ g(u) = 0. \end{align*}

Поскольку $$\mu(u) > 0, \forall u \in U,$$ то корни уравнений совпадают.

Далее для простоты будем считать, что $$n = 2$$, т.к. доказательство легко обобщается на случай произвольного $$n$$.

Найдем матрицу Якоби системы \eqref{sys1}.

\begin{equation*} J_1(u_1, u_2) = \left.\left[\dfrac{\partial g}{\partial u}\right]\right|_{(u_1, u_2)} = \left.\left[\dfrac{\partial (\mu f)}{\partial u}\right]\right|_{(u_1, u_2)} = \left.\begin{pmatrix} \dfrac{\partial \mu}{\partial u_1}f_1 + \dfrac{\partial f_1}{\partial u_1}\mu & \dfrac{\partial \mu}{\partial u_2}f_1 + \dfrac{\partial f_1}{\partial u_2}\mu\\ \dfrac{\partial \mu}{\partial u_1}f_2 + \dfrac{\partial f_2}{\partial u_1}\mu & \dfrac{\partial \mu}{\partial u_2}f_2 + \dfrac{\partial f_2}{\partial u_2}\mu \end{pmatrix}\right|_{(u_1,u_2)}. \end{equation*}

Если точка $$(u_1, u_2)$$ является особой, то $$f_1(u_1, u_2) = f_2(u_1, u_2) = 0.$$ Тогда матрица Якоби системы \eqref{sys1} равна

\begin{equation*} J_1(u_1, u_2) = \left.\begin{pmatrix} \dfrac{\partial f_1}{\partial u_1}\mu & \dfrac{\partial f_1}{\partial u_2}\mu\\ \dfrac{\partial f_2}{\partial u_1}\mu & \dfrac{\partial f_2}{\partial u_2}\mu \end{pmatrix}\right|_{(u_1,u_2)} = (\mu(u_1, u_2))^2 \left.\begin{pmatrix} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} \end{pmatrix}\right|_{(u_1,u_2)} = (\mu(u_1, u_2))^2 J_2(u_1,u_2), \end{equation*}

где $$J_2(u_1, u_2)$$ — матрица Якоби системы \eqref{sys2}. Поскольку $$\mu(u_1, u_2) > 0$$, то знаки собственных значений матриц Якоби систем \eqref{sys1} и \eqref{sys2} одинаковы. Поэтому особые точки имеют одинаковый характер устойчивости. Значит, системы \eqref{sys1} и \eqref{sys2} топологически эквивалентны.

Таким образом, орбитально эквивалентные системы являются топологически эквивалентными, поэтому их называют топологически орбитально эквивалентными.

Замечание. Можно понимать орбитальную эквивалентность как нелинейную деформацию времени. Так, если в системе \eqref{sys1} сделать замену $$t = \mu(u)\tau, \operatorname{d}t = \mu(u)\operatorname{d}\tau,$$ то получим систему \eqref{sys2}. Таким образом, траектории орбитально эквивалентных систем отличаются лишь скоростью прохождения по ним.

Утверждение. Если в области $$U$$ выполнено неравенство $$\dfrac{\partial (\mu f_1)}{\partial u_1} +\dfrac{\partial (\mu f_2)}{\partial u_2} > 0 ($$или $$< 0),$$ то в ней нет замкнутых траекторий системы \eqref{sys1}.

Доказательство. Заметим, что левая часть указанного неравенства есть дивергенция правой части системы \eqref{sys1} $$\implies$$ по теореме Дюлака-Бендиксона в области $$U$$ нет замкнутых траекторий системы.

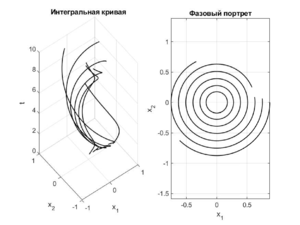
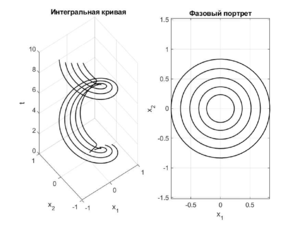
Пример

Рассмотрим две системы: \begin{equation} \begin{cases}\label{first_sys_1} \dot{x}_1 = x_2(1-(x_1^2+x_2^2)),\\ \dot{x}_2 = -x_1(1-(x_1^2+x_2^2)) \end{cases}\\ \end{equation} \begin{equation} \begin{cases}\label{second_sys_1} \dot{x}_1 = x_2,\\ \dot{x}_2 = -x_1 \end{cases} \end{equation} Эти системы топологически орбитально эквивалентны в области $$U = \{(x_1,x_2)\mid x_1^2 + x_2^2 < 1\}.$$ Смотря на интегральные кривые, можно заметить, что скорость прохождения по траекториям системы \eqref{first_sys_1} меньше, чем скорость прохождения по траекториям системы \eqref{second_sys_1}.

Интегральная кривая и фазовый портрет системы \eqref{first_sys_1} в области $$U$$

Интегральная кривая и фазовый портрет системы \eqref{second_sys_1} в области $$U$$

Список литературы

1. Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2024.
2. Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.