Циклы в системах с дискретным временем. Теорема Шарковского
Содержание
Понятие цикла
Пусть задана следующая динамическая система с дискретным временем:\[
\begin{equation}
\begin{cases}
v_{t+1}=f(v_t),\ \ t=0,1,2,...\\
v|_{t=0}=v_0,
\end{cases} \label{sys1}
\end{equation}
\]
где \( f: v \mapsto f(v),\ v\in{U}\subset\mathbb R^n,\ f:U\to U \).
Определение 1. Несовпадающие точки \(v_1,v_2,...,v_k\) фазового пространства системы \((\ref{sys1})\) образуют цикл длины \(k\), если \(f(v_1)=v_2,\ f(v_2)=v_3,...,\ f(v_{k-1})=v_k,\ f(v_k)=v_1\).
Обозначим за \(f^k\) \(k\)-ю степень отображения \(f\): $$f^k(v) = \overbrace{f(f(...f(f}^{k\ раз}(v))))$$. Тогда если в системе \((\ref{sys1})\) есть цикл длины \(k\), где \( v_i\) — неподвижные точки этого цикла, \(i\in\overline{1,k}\), то:
- \(f(v_i)=f^{i-1}(v_1)\), то есть любая точка цикла получается из первой (вообще говоря, любой) его точки несколькими итерациями применения отображения \(f\);
- \(f^k(v_i)=v_i\), что как раз показывает цикличность этого отображения — через \(k\) итераций мы возвращаемся в ту же точку, откуда стартовали, вне зависимости от самой точки.
Устойчивость цикла
Свойство устойчивости цикла неразрывно связано с терминами устойчивости составляющих его точек.
Определение 2.
Цикл длины \(k\) называют устойчивым, если устойчивы составляющие его неподвижные точки отображения \(f^k\).
Вычислим для начала для \(1\)-й неподвижной точки \(v_1\) производную отображения \(f^k\):\[(f^k(v_1))'=\left(f(f^{k-1}(v_1))\right)'=[по\ формуле\ производной\ сложной\ функции]=
f'(f^{k-1}(v_1)) \cdot (f^{k-1}(v_1))' = f'(f^{k-1}(v_1)) \cdot f'(f^{k-2}(v_1)) \cdot (f^{k-2}(v_1))' =
\]
\[
=\ ...\ = f'(\overbrace{f^{k-1}(v_1)}^{v_k}) \cdot f'(\overbrace{f^{k-2}(v_1)}^{v_{k-1}}) \cdot ... \cdot f'(v_1)\ =\ f'(v_k)f'(v_{k-1}) \cdot ... \cdot f'(v_1).
\]
Как уже было описано выше, рассматриваемая конструкция обладает свойством цикличности. Это можно переформулировать как симметричность цикла относительно любой его точки. Поэтому будет получен тот же результат, если будем считать производную \(f^k\) не в точке \(v_1\), а в любой другой точке цикла. Также не стоит забывать, что для проверки неподвижной точки на устойчивость необходимо взять модуль полученной производной и сравнить его с единицей.
Таким образом, для проверки цикла на устойчивость проводится следующее сравнение:\[|f'(v_k)f'(v_{k-1})...f'(v_1)|\vee 1.\]
Выводы о характере устойчивости, в зависимости от полученного неравенства, можно сделать следующие:
- если получен знак $$<$$, то устойчивость цикла асимптотическая;
- если получен знак $$>$$, то цикл является неустойчивым;
- в противном случае, если получен знак равенства, то требуются дополнительные исследования устойчивости цикла.
Теорема Шарковского
При анализе существования циклов разных длин полезна теорема Шарковского. Прежде, чем её формулировать, введём упорядочивание всех натуральных чисел особым образом:
$$
\begin{array}{ll}
3\succ5\succ7\succ...\succ & \text{все нечетные числа, кроме 1} \\
\succ 2\cdot3\succ2\cdot5\succ2\cdot7\succ...\succ & \text{все нечетные числа, умноженные на 2, кроме 1} \\
\succ 2^2\cdot3\succ2^2\cdot5\succ2^2\cdot7\succ...\succ & \text{все нечетные числа, умноженные на } 2^2\text{, кроме 1} \\
\succ 2^3\cdot3\succ2^3\cdot5\succ2^3\cdot7\succ...\succ & \text{все нечетные числа, умноженные на } 2^3\text{, кроме 1} \\
\succ...\succ & \\
\succ2^3\succ2^2\succ2\succ1. &
\end{array}
$$
Определение 2. Такое упорядочивание называют упорядочиванием по Шарковскому.
Теорема Шарковского.
Пусть функция \(f\), задающая систему \((\ref{sys1})\), непрерывна. Если в такой дискретной динамической системе есть цикл длины \(k\), то в ней есть и циклы любых длин, стоящих после \(k\) в порядке по Шарковскому.
Доказательство этой теоремы можно найти в [1].
Замечание. Теорема Шарковского ничего не говорит об устойчивости каких-либо циклов в исследуемой системе.
Следствие 1.
Если в системе есть цикл длины \(3\), то есть и цикл любой другой длины, что рождает хаос в системе.
Следствие 2.
Если в системе нет циклов длины \(2\), то циклы в системе отсутствуют вовсе.
Поэтому на начальном этапе исследования системы на наличие циклов особый интерес представляют циклы именно этих длин.
Пример исследования системы на предмет циклов
Продемонстрируем применение определения цикла на отображении, относящемся к классу так называемых логистических отображений. Рассматриваемое нами задаётся следующим уравнением:\[ v_{t+1} = rv_t(1-v_t^3).\] Уравнение для поиска неподвижной точки тогда будет выглядеть следующим образом:\[v^* = rv^*(1-{v^*}^3).\]
Решим это уравнение:\[
v^*(1 - r + r{v^*}^3) = 0 \Leftrightarrow
\left[
\begin{array}{l}
v^* = 0, \\
v^* = \sqrt[3]{1-\frac{1}{r}}. \\
\end{array}\right.
\]
Таким образом, получены две неподвижные точки: $$v^*_1 = 0,\ v^*_2 = \sqrt[3]{1-\frac{1}{r}}$$.
Наличие цикла длины 2
Для проверки наличия цикла длины $$2$$ необходимо решить уравнение $$f(f(v))=v$$, причем найти корни, не совпадающие с уже найденными $$v_1^*$$ и $$v_2^*$$.\[
f(f(v))=v \ \ \Rightarrow \ \ r\left(rv\left(1-v^3\right)\right)\left(1-\left(rv\left(1-v^3\right)\right)^3\right)=v \ \ \Rightarrow
\ \ v\left( r^2\left(1-v^3\right)\left(1-\left(rv\left(1-v^3\right)\right)^3\right) - 1 \right) = 0.
\]
Аналитическое получение решения данного уравнения достаточно трудоёмко. В таких случаях помогает качественный анализ функции $$g(v)=f(f(v))$$. Её производная по $$v$$ после упрощений выглядит следующим образом:\[
\frac{\partial g(v)}{\partial v} = r^2 v (1 - v^3) (1 - (r v (1 - v^3))^3).
\]
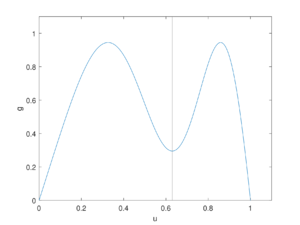
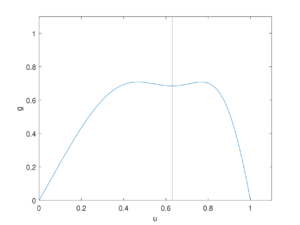
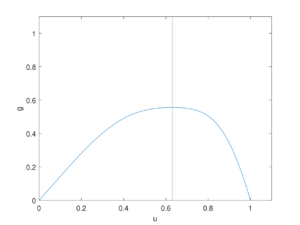
Она всегда обращается в ноль при $$v=\sqrt[3]{\frac{1}{4}}$$ — в этой точке всегда будем иметь экстремум функции $$g(v)=f(f(v))$$. Два других возникают по разные стороны от $$v=\sqrt[3]{\frac{1}{4}}$$ при $$r>\frac{4}{3}$$. При $$r\in(0,\frac{4}{3}]$$ у $$g(v)$$ всего $$1$$ экстремальная точка. На графиках справа наглядно представлено изменение количества точек, где производная обращается в $$0$$, в зависимости от $$r$$.
Вернемся к уравнению $$g(v)=v$$. У него всегда есть $$2$$ решения, совпадающих с $$v_1^*$$ и $$v_2^*$$. Значит, для существования цикла длины $$2$$ необходимо существование ещё двух действительных решений этого уравнения. При этом из проведенного исследования видно, что $$r$$ должно быть как минимум больше $$\frac{4}{3}$$, иначе будет только $$2$$ пересечения с биссектрисой первой координатной четверти — в уже упомянутых точках. Численно можно установить, что при $$r>\tilde{r}\approx \frac{5}{3}$$ решений у рассматриваемого уравнения будет уже $$4$$. Значит, при таких $$r$$ в системе будет образовываться цикл длины $$2$$. При $$r\leqslant\tilde{r}$$ цикла длины $$2$$ образовываться не будет.
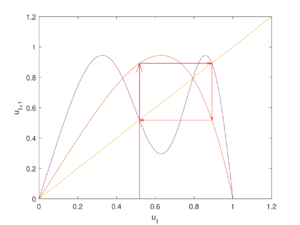
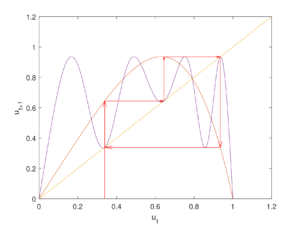
Приведём пример цикла длины $$2$$ при $$r=2$$. Его составляют две точки:
$$v_{1}' = \frac{1}{2} \sqrt[3]{7 - \sqrt{13} - \sqrt{2 (\sqrt{13} - 1)}}$$ и $$v_{2}' = \frac{1}{2} \sqrt[3]{7 - \sqrt{13} + \sqrt{2 (\sqrt{13} - 1)}}$$. Этот случай проиллюстрирован на графике ниже.
Устойчивость цикла длины 2
Проверим цикл длины $$2$$ системы на устойчивость. Для этого надо исследовать функцию $$q(v, r) = f'(v_{r,1}')f'(v_{r,2}')$$ (где $$v_{r,i}'$$ — $$i$$-я точка цикла, записанная в общем виде для произвольного $$r$$) и проверим, при каких $$r$$ она будет лежать в отрезке $$[-1,1]$$. Значения $$r$$ берутся из луча $$(\frac{5}{3},+\infty)$$ — при этих значениях параметра существует цикл длины $$2$$.
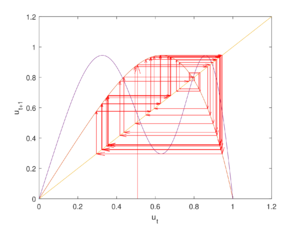
В данном примере цикл длины $$2$$ неустойчив на всей области определения, поскольку $$|q(v, r)| > 60\ \forall r$$ из описанного промежутка, что нетрудно проверить. В качестве иллюстрации неустойчивости цикла при $$r=2$$ приведен рисунок ниже, где в качестве начальной точки взята точка $$\tilde{v} = v_{1}' - 0.01$$. При небольшом смещении от начального положения цикла траектории не приближаются к траекториям цикла.
Наличие цикла длины 3
Аналогично действиям при нахождении цикла длины $$2$$, необходимо найти решения уравнения $$f^{(3)}(v)=v$$, не совпадающие с неподвижными точками заданной системы. Аналитически это уравнение решается достаточно сложно, поэтому полезным будет применить графический подход, аналогичный уже рассмотренному.
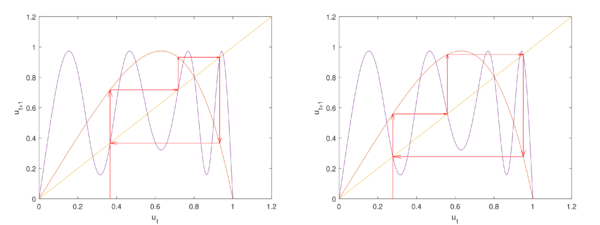
При $$r\approx \overline{r}=1.981$$ график $$f^{(3)}(v)$$ касается $$h(v)=v$$ в $$3$$-х точках одновременно. При этом возникает цикл длины $$3$$ (график справа), состоящий из точек $$\{0.3383,0.6442,0.9352\}$$. При $$r\in(1,\overline{r})$$ в заданной системе цикла длины $$3$$ не существует.
Если $$r>\overline{r}$$, то решений у исследуемого нами уравнения будет $$6$$. При таких значениях параметра будут образовываться $$2$$ цикла длины $$3$$. На графиках ниже представлены $$2$$ цикла для $$r=2.06$$: $$\{0.277252,0.558967,0.950372\},$$ и $$\{0.366477,0.717785,0.931817\}$$.
Устойчивость цикла длины 3
Для проверки цикла длины $$3$$ на устойчивость проведем аналогичные анализу на устойчивость цикла длины $$2$$ действия. Исследуется функция $$q(v, r) = f'(v_{r,1}')f'(v_{r,2}')f'(v_{r,3}')$$, ищутся такие $$r$$, при которых её значения будут лежать в отрезке $$[-1,1]$$.
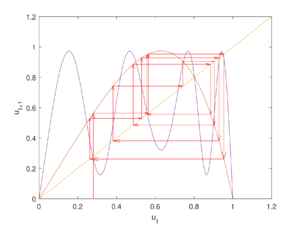
Проведя эти рассуждения, получается, что при $$r\in[1.981,+\infty)$$ циклы длины $$3$$ будут неустойчивыми. Это иллюстрирует рисунок справа — траектории цикла, выпущенного вблизи одной из его точек (из $$v=0.28$$) не приближаются к траекториям цикла, наблюдаемого на предыдущем рисунке.
Существование циклов других длин
Согласно приведенной ранее теореме Шарковского и её следствиям, в рассматриваемой системе имеются циклы всех возможных длин при соответствующих им значениях параметра $$r$$, так как существует цикл длины $$3$$. При этом из существования цикла длины $$3$$ действительно следует существование цикла длины $$2$$ — область существования цикла длины $$3$$ входит в область существования в системе цикла длины $$2$$.
Список литературы
- К. Бернс, Б. Хассельблатт, "Теорема Шарковского: естественное прямое доказательство", 2008.
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2023.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011