Поляра множества и ее свойства: различия между версиями
Vlad22 (обсуждение | вклад) |
Vlad22 (обсуждение | вклад) |
||
| (не показано 7 промежуточных версий этого же участника) | |||
| Строка 7: | Строка 7: | ||
== Примеры == | == Примеры == | ||
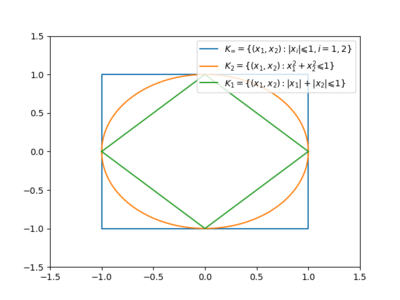
| − | + | [[Файл:Polar k2.png|400px|thumb|frame|right|$$K_1^\circ = K_\infty, ~K_2^\circ = K_2, ~K_\infty^\circ = K_1$$]] | |
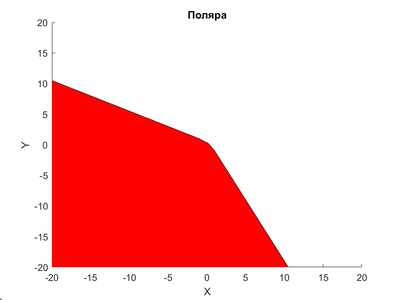
| + | [[Файл:Infty polar.png|400px|thumb|frame|right|Поляра ромба с параметрами $$a = (1,1), c = (1,1)$$]] | ||
# $$ (\bar{B}_r(0))^{\circ} = \bar{B}_{1/r}(0)$$, где $$B_r(0)$$ − шар радиуса $$r$$ с центром в нуле; | # $$ (\bar{B}_r(0))^{\circ} = \bar{B}_{1/r}(0)$$, где $$B_r(0)$$ − шар радиуса $$r$$ с центром в нуле; | ||
# $$ \{0\}^{\circ} = \mathbb{R}^n$$; | # $$ \{0\}^{\circ} = \mathbb{R}^n$$; | ||
| − | # | + | # для $$p \neq 0, \{p\}^{\circ}$$ − замкнутое полупространство:\begin{gather*} |
\{p\}^{\circ} = \{x \in \mathbb{R}^n : \langle x,p \rangle \leqslant 1 \};\end{gather*} | \{p\}^{\circ} = \{x \in \mathbb{R}^n : \langle x,p \rangle \leqslant 1 \};\end{gather*} | ||
| − | # | + | # если $$A$$ − линейное подпространство, то $$A^{\circ} = A^{\perp}$$; |
| + | # пусть $$R$$ − ромб с центром в точке $$c=(c_1, c_2)$$ и диагоналями длины $$a_1, a_2$$:\begin{gather*} | ||
| + | R = \left\{ | ||
| + | x \in \mathbb{R}^2~\Big| ~\sum_{i=1}^2\frac{2|x_i-c_i|}{a_i} \leqslant 1 | ||
| + | \right\}. | ||
| + | \end{gather*} Тогда поляра ромба имеет вид:\begin{gather*} | ||
| + | R^{\circ} = | ||
| + | \left\{ | ||
| + | l \in \mathbb{R}^2~\Big|~ | ||
| + | \max_{i=1,2}\frac{|a_il_i|}{2} + \langle l, c \rangle \leqslant 1 | ||
| + | \right\}. | ||
| + | \end{gather*} | ||
| + | # Поляра может быть неограниченным множеством. Пример − ромб с параметрами $$a = (1,1), c = (2,2)$$. Из формулы в прошлом примере следует, что границу поляры будет задавать кривая: $$\max\{x(\frac{a_1}{2} + c_1) + yc_2, xc_1 + y(\frac{a_2}{2} + c_2)\} = 1$$. | ||
== Свойства == | == Свойства == | ||
1. Если $$\lambda > 0$$, то $$(\lambda A)^{\circ} = \frac{1}{\lambda}A^{\circ}$$. | 1. Если $$\lambda > 0$$, то $$(\lambda A)^{\circ} = \frac{1}{\lambda}A^{\circ}$$. | ||
| Строка 20: | Строка 33: | ||
3. '''Антимонотонность:''' если $$A \subset B$$, то $$A^{\circ} \supset B^{\circ}$$. | 3. '''Антимонотонность:''' если $$A \subset B$$, то $$A^{\circ} \supset B^{\circ}$$. | ||
| − | '''Следствие 1.''' Если $$A$$ − ограничено, то $$0 \in | + | '''Следствие 1.''' Если $$A$$ − ограничено, то $$0 \in \mathrm{int}(A^{\circ})$$. |
| − | ''' | + | '''Доказательство:''' |
| − | $$A$$ ограничено $$\Rightarrow \exists R > 0: A \subset \bar{B}_R(0)$$. | + | $$A$$ ограничено $$\Rightarrow \exists R > 0: A \subset \bar{B}_R(0)$$. Тогда из свойства антимонотонности: $$A^{\circ} \supset \bar{B}_{1/R}(0)$$. Тогда $$0 \in \mathrm{int}(A^{\circ})$$. $$\blacksquare$$ |
| − | '''Следствие 2.''' Если $$0 \in | + | '''Следствие 2.''' Если $$0 \in \mathrm{int}(A)$$, то $$A^{\circ}$$ ограничено. |
| − | ''' | + | '''Доказательство:''' |
| − | $$0 \in | + | $$0 \in \mathrm{int}(A) \Rightarrow \exists r > 0: \bar{B}_r(0) \subset A$$. Тогда $$A^{\circ} \subset \bar{B}_{1/r}(0) \Rightarrow A^{\circ}$$ − ограничено. $$\blacksquare$$ |
4. '''Поляра объединения множеств:''' $$\forall A,B \subset \mathbb{R}^n, (A \cup B)^{\circ} = A^{\circ} \cap B^{\circ}$$. | 4. '''Поляра объединения множеств:''' $$\forall A,B \subset \mathbb{R}^n, (A \cup B)^{\circ} = A^{\circ} \cap B^{\circ}$$. | ||
| − | ''' | + | '''Доказательство:''' |
\begin{gather*} | \begin{gather*} | ||
(A \cup B)^{\circ} = \{x \in \mathbb{R}^n: \forall a \in (A \cup B), \langle x, a \rangle \leqslant 1\} = \{x \in \mathbb{R}^n: \forall a \in A, \langle x, a \rangle \leqslant 1\} \cap \{x \in \mathbb{R}^n: \forall a \in B, \langle x, a \rangle \leqslant 1\} = A^{\circ} \cap B^{\circ}. | (A \cup B)^{\circ} = \{x \in \mathbb{R}^n: \forall a \in (A \cup B), \langle x, a \rangle \leqslant 1\} = \{x \in \mathbb{R}^n: \forall a \in A, \langle x, a \rangle \leqslant 1\} \cap \{x \in \mathbb{R}^n: \forall a \in B, \langle x, a \rangle \leqslant 1\} = A^{\circ} \cap B^{\circ}. | ||
| − | \end{gather*} | + | \end{gather*} $$\blacksquare$$ |
'''Примечание:''' свойство выполняется в случае бесконечных объединений − пусть $$A = \cup A_i$$, тогда $$(\cup A_i)^{\circ} = \cap A_i^{\circ}$$. Доказывается аналогично. | '''Примечание:''' свойство выполняется в случае бесконечных объединений − пусть $$A = \cup A_i$$, тогда $$(\cup A_i)^{\circ} = \cap A_i^{\circ}$$. Доказывается аналогично. | ||
| Строка 43: | Строка 56: | ||
'''Следствие:''' поляра любого множества замкнута, выпукла и содержит 0. | '''Следствие:''' поляра любого множества замкнута, выпукла и содержит 0. | ||
| − | ''' | + | '''Доказательство:''' |
| − | Представим множество $$A$$ в виде $$A = \cup_{x \in A} \{x\}$$. Тогда $$A^{\circ} = \cap_{x \in A} \{x\}^{\circ}$$ − пересечение замкнутых полупространств, содержащих ноль. | + | Представим множество $$A$$ в виде $$A = \cup_{x \in A} \{x\}$$. Тогда $$A^{\circ} = \cap_{x \in A} \{x\}^{\circ}$$ − пересечение замкнутых полупространств, содержащих ноль. $$\blacksquare$$ |
| − | 5. | + | 5. '''Теорема о биполяре:''' для того чтобы $$A^{\circ\circ} = A$$, необходимо и достаточно, чтобы $$A$$ было выпуклым замкнутым множеством, содержащим нуль. |
| + | |||
| + | '''Доказательство:''' | ||
| + | # Докажем, что $$A \subset A^{\circ\circ}$$. Если $$a \in A$$, то $$\forall b \in A^{\circ}: \langle a,b \rangle \leqslant 1$$. Из определения поляры легко следует, что $$a \in A^{\circ\circ}$$. | ||
| + | # Докажем, что $$A \supset A^{\circ\circ}$$. Пусть $$\exists p \in A^{\circ\circ} \backslash A$$. Существует гиперплоскость $$H$$, строго отделяющая $$A$$ от $$p$$. Так как $$0 \in A$$, $$0 \notin H$$. Тогда $$H$$ имеет вид | ||
| + | \begin{gather*} | ||
| + | H = \{x \in \mathbb{R}^n:\langle x, v \rangle = 1\}, | ||
| + | \end{gather*} | ||
| + | где $$v \in \mathbb{R}^n$$. | ||
| + | Пусть $$H^+ = \{x \in \mathbb{R}^n:\langle x, v \rangle > 1\}$$, $$H^- = \{x \in \mathbb{R}^n:\langle x, v \rangle < 1\}$$. | ||
| + | $$0 \in H^- \Rightarrow A \subset H^-, p \in H^+$$. $$A \subset H^- \Rightarrow \langle a, v \rangle < 1, \forall a \in A$$. Поэтому $$ v \in A^{\circ}$$. $$p \in H^+ \Rightarrow \langle p, v \rangle > 1$$. Поэтому $$p \notin A^{\circ\circ}$$, что противоречит начальному предположению. | ||
== Операции над множеством, не меняющие поляру == | == Операции над множеством, не меняющие поляру == | ||
1. $$(A \cup \{0\})^{\circ} = A^{\circ} $$. | 1. $$(A \cup \{0\})^{\circ} = A^{\circ} $$. | ||
| − | ''' | + | '''Доказательство:''' $$(A \cup \{0\})^{\circ} = A^{\circ} \cap \{0\}^{\circ} = A^{\circ}$$. $$\blacksquare$$ |
| − | 2. $$(conv(A))^{\circ} = A^{\circ}$$. | + | 2. $$(\mathrm{conv}(A))^{\circ} = A^{\circ}$$. |
| − | ''' | + | '''Доказательство:''' из свойства 2 и равенства $$\rho(y,A) = \rho(y,\mathrm{conv}(A))$$. $$\blacksquare$$ |
| − | 3. $$ | + | 3. ($$\mathrm{cl}(A))^{\circ} = A^{\circ}$$. |
| − | ''' | + | '''Доказательство:''' |
| − | * Докажем, что $$A^{\circ} \subset ( | + | * Докажем, что $$A^{\circ} \subset (\mathrm{cl}(A))^{\circ}$$. Пусть $$p \in \mathrm{cl}(A) \Rightarrow p = \lim_{i \rightarrow \infty} a_i, a_i \in A$$. Рассмотрим скалярное произведение $$\langle x, p \rangle$$, $$\forall x \in A^{\circ}, \forall p \in \mathrm{cl}(A)$$: |
\begin{gather*} | \begin{gather*} | ||
\langle x, p \rangle = \langle x, \lim_{i \rightarrow \infty} a_i \rangle = \lim_{i \rightarrow \infty} \langle x, a_i \rangle \leqslant 1. | \langle x, p \rangle = \langle x, \lim_{i \rightarrow \infty} a_i \rangle = \lim_{i \rightarrow \infty} \langle x, a_i \rangle \leqslant 1. | ||
\end{gather*} | \end{gather*} | ||
| − | Следовательно, $$A^{\circ} \subset ( | + | Следовательно, $$A^{\circ} \subset (\mathrm{cl}(A))^{\circ}$$. |
| − | * $$A \subset | + | * $$A \subset \mathrm{cl}(A)$$, следовательно, по свойству антимонотонности: $$A^{\circ} \supset (\mathrm{cl}(A))^{\circ}$$. |
| − | Из этого следует доказываемое утверждение. | + | Из этого следует доказываемое утверждение. $$\blacksquare$$ |
| + | |||
| + | == Список литературы == | ||
| + | # Магарил-Ильяев Г. Г., Тихомиров В. М. "Выпуклый анализ и его приложения", М.: Едиториал УРСС, 2003. | ||
Текущая версия на 22:25, 19 декабря 2022
Содержание
Определение
Пусть $$A$$ непустое подмножество $$\mathbb{R}^n$$. Полярой множества $$A$$ называется множество \[ A^{\circ}=\left\{y \in \mathbb{R}^n~|~ \langle x, y \rangle \leqslant 1 , \forall x \in A\right\}. \] Поляра множества $$A^{\circ}$$ называется биполярой $$A$$.
Примеры
- $$ (\bar{B}_r(0))^{\circ} = \bar{B}_{1/r}(0)$$, где $$B_r(0)$$ − шар радиуса $$r$$ с центром в нуле;
- $$ \{0\}^{\circ} = \mathbb{R}^n$$;
- для $$p \neq 0, \{p\}^{\circ}$$ − замкнутое полупространство:\begin{gather*} \{p\}^{\circ} = \{x \in \mathbb{R}^n : \langle x,p \rangle \leqslant 1 \};\end{gather*}
- если $$A$$ − линейное подпространство, то $$A^{\circ} = A^{\perp}$$;
- пусть $$R$$ − ромб с центром в точке $$c=(c_1, c_2)$$ и диагоналями длины $$a_1, a_2$$:\begin{gather*} R = \left\{ x \in \mathbb{R}^2~\Big| ~\sum_{i=1}^2\frac{2|x_i-c_i|}{a_i} \leqslant 1 \right\}. \end{gather*} Тогда поляра ромба имеет вид:\begin{gather*} R^{\circ} = \left\{ l \in \mathbb{R}^2~\Big|~ \max_{i=1,2}\frac{|a_il_i|}{2} + \langle l, c \rangle \leqslant 1 \right\}. \end{gather*}
- Поляра может быть неограниченным множеством. Пример − ромб с параметрами $$a = (1,1), c = (2,2)$$. Из формулы в прошлом примере следует, что границу поляры будет задавать кривая: $$\max\{x(\frac{a_1}{2} + c_1) + yc_2, xc_1 + y(\frac{a_2}{2} + c_2)\} = 1$$.
Свойства
1. Если $$\lambda > 0$$, то $$(\lambda A)^{\circ} = \frac{1}{\lambda}A^{\circ}$$.
2. $$A^{\circ} = \{y \in \mathbb{R}^n | \rho(y,A) \leqslant 1\}$$, где $$\rho$$ — опорная функция.
3. Антимонотонность: если $$A \subset B$$, то $$A^{\circ} \supset B^{\circ}$$.
Следствие 1. Если $$A$$ − ограничено, то $$0 \in \mathrm{int}(A^{\circ})$$.
Доказательство:
$$A$$ ограничено $$\Rightarrow \exists R > 0: A \subset \bar{B}_R(0)$$. Тогда из свойства антимонотонности: $$A^{\circ} \supset \bar{B}_{1/R}(0)$$. Тогда $$0 \in \mathrm{int}(A^{\circ})$$. $$\blacksquare$$
Следствие 2. Если $$0 \in \mathrm{int}(A)$$, то $$A^{\circ}$$ ограничено.
Доказательство:
$$0 \in \mathrm{int}(A) \Rightarrow \exists r > 0: \bar{B}_r(0) \subset A$$. Тогда $$A^{\circ} \subset \bar{B}_{1/r}(0) \Rightarrow A^{\circ}$$ − ограничено. $$\blacksquare$$
4. Поляра объединения множеств: $$\forall A,B \subset \mathbb{R}^n, (A \cup B)^{\circ} = A^{\circ} \cap B^{\circ}$$.
Доказательство: \begin{gather*} (A \cup B)^{\circ} = \{x \in \mathbb{R}^n: \forall a \in (A \cup B), \langle x, a \rangle \leqslant 1\} = \{x \in \mathbb{R}^n: \forall a \in A, \langle x, a \rangle \leqslant 1\} \cap \{x \in \mathbb{R}^n: \forall a \in B, \langle x, a \rangle \leqslant 1\} = A^{\circ} \cap B^{\circ}. \end{gather*} $$\blacksquare$$
Примечание: свойство выполняется в случае бесконечных объединений − пусть $$A = \cup A_i$$, тогда $$(\cup A_i)^{\circ} = \cap A_i^{\circ}$$. Доказывается аналогично.
Следствие: поляра любого множества замкнута, выпукла и содержит 0.
Доказательство:
Представим множество $$A$$ в виде $$A = \cup_{x \in A} \{x\}$$. Тогда $$A^{\circ} = \cap_{x \in A} \{x\}^{\circ}$$ − пересечение замкнутых полупространств, содержащих ноль. $$\blacksquare$$
5. Теорема о биполяре: для того чтобы $$A^{\circ\circ} = A$$, необходимо и достаточно, чтобы $$A$$ было выпуклым замкнутым множеством, содержащим нуль.
Доказательство:
- Докажем, что $$A \subset A^{\circ\circ}$$. Если $$a \in A$$, то $$\forall b \in A^{\circ}: \langle a,b \rangle \leqslant 1$$. Из определения поляры легко следует, что $$a \in A^{\circ\circ}$$.
- Докажем, что $$A \supset A^{\circ\circ}$$. Пусть $$\exists p \in A^{\circ\circ} \backslash A$$. Существует гиперплоскость $$H$$, строго отделяющая $$A$$ от $$p$$. Так как $$0 \in A$$, $$0 \notin H$$. Тогда $$H$$ имеет вид
\begin{gather*} H = \{x \in \mathbb{R}^n:\langle x, v \rangle = 1\}, \end{gather*} где $$v \in \mathbb{R}^n$$. Пусть $$H^+ = \{x \in \mathbb{R}^n:\langle x, v \rangle > 1\}$$, $$H^- = \{x \in \mathbb{R}^n:\langle x, v \rangle < 1\}$$. $$0 \in H^- \Rightarrow A \subset H^-, p \in H^+$$. $$A \subset H^- \Rightarrow \langle a, v \rangle < 1, \forall a \in A$$. Поэтому $$ v \in A^{\circ}$$. $$p \in H^+ \Rightarrow \langle p, v \rangle > 1$$. Поэтому $$p \notin A^{\circ\circ}$$, что противоречит начальному предположению.
Операции над множеством, не меняющие поляру
1. $$(A \cup \{0\})^{\circ} = A^{\circ} $$.
Доказательство: $$(A \cup \{0\})^{\circ} = A^{\circ} \cap \{0\}^{\circ} = A^{\circ}$$. $$\blacksquare$$
2. $$(\mathrm{conv}(A))^{\circ} = A^{\circ}$$.
Доказательство: из свойства 2 и равенства $$\rho(y,A) = \rho(y,\mathrm{conv}(A))$$. $$\blacksquare$$
3. ($$\mathrm{cl}(A))^{\circ} = A^{\circ}$$.
Доказательство:
- Докажем, что $$A^{\circ} \subset (\mathrm{cl}(A))^{\circ}$$. Пусть $$p \in \mathrm{cl}(A) \Rightarrow p = \lim_{i \rightarrow \infty} a_i, a_i \in A$$. Рассмотрим скалярное произведение $$\langle x, p \rangle$$, $$\forall x \in A^{\circ}, \forall p \in \mathrm{cl}(A)$$:
\begin{gather*} \langle x, p \rangle = \langle x, \lim_{i \rightarrow \infty} a_i \rangle = \lim_{i \rightarrow \infty} \langle x, a_i \rangle \leqslant 1. \end{gather*} Следовательно, $$A^{\circ} \subset (\mathrm{cl}(A))^{\circ}$$.
- $$A \subset \mathrm{cl}(A)$$, следовательно, по свойству антимонотонности: $$A^{\circ} \supset (\mathrm{cl}(A))^{\circ}$$.
Из этого следует доказываемое утверждение. $$\blacksquare$$
Список литературы
- Магарил-Ильяев Г. Г., Тихомиров В. М. "Выпуклый анализ и его приложения", М.: Едиториал УРСС, 2003.