Отделимость множеств

В выпуклом анализе значительную роль играют теоремы об отделимости выпуклых множеств.

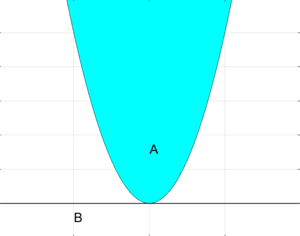
Отделимость выпуклых множеств $$A, \, B \subset \mathbb R ^ 2$$. Множество $$A$$ – надграфик функции $$y = x ^ 2$$ при $$x \in \mathbb R$$, выделено голубым цветом; множество $$B$$ – прямая $$y = 0$$, выделено чёрным цветом.

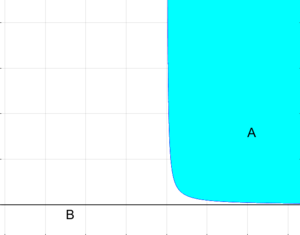
Строгая отделимость выпуклых множеств $$A, \, B \subset \mathbb R ^ 2$$. Множество $$A$$ – надграфик функции $$y = \displaystyle \frac{1}{x}$$ при $$x > 0$$, выделено голубым цветом; множество $$B$$ – прямая $$y = 0$$, выделено чёрным цветом.

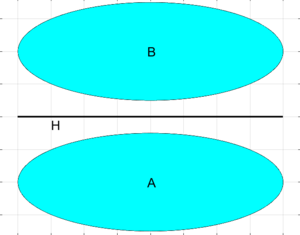
Сильная отделимость выпуклых множеств $$A, \, B \subset \mathbb R ^ 2$$. Множества $$A, \, B$$ – эллипсы, выделены голубым цветом; множество H – часть одной из прямых (гиперплоскостей в $$\mathbb R ^ 2$$), разделяющих $$А$$ и $$В$$, выделено черным цветом.

Определения

Пусть $$X = (X, \, ||\cdot||)$$ – нормированное вещественное пространство , множества $$A, \, B \subset X$$.

Открытый шар в пространстве $$X$$ с центром в $$x \in X$$ и радиусом $$R$$ обозначим так: $$O(x, \, R) := \{y \in X \, | \, ||y - x|| < R \}$$. Замкнутый шар в пространстве $$X$$ с центром в $$x \in X$$ и радиусом $$R$$ обозначим так: $$B(x, \, R) := \{y \in X \, | \, ||y - x|| \leqslant R \}$$.

Определение 1. Аффинной комбинацией точек $$x_1, x_2, \ldots, x_n \in X$$ назовём выражение $$\displaystyle \sum_{i = 1} ^ n \alpha_i x_i$$, где числа $$\alpha_1, \alpha_2, \ldots, \alpha_n$$ удовлетворяют условию $$\sum_{i = 1} ^ n \alpha_i = 1$$.

Определение 2. Аффинной оболочкой множества $$A$$ назовём множество всевозможных аффинных комбинаций точек множества $$A: \, aff A := \{\displaystyle \sum_{i = 1} ^ n \alpha_i x_i \, | \, n \in \mathbb N, \, x_1, \, x_2, \ldots, x_n \in X, \, \alpha_1, \, \alpha_2, \ldots, \alpha_n \in \mathbb R, \, \displaystyle \sum_{i = 1} ^ n \alpha_i = 1\}$$.

Определение 3. Относительной внутренностью множества $$A$$ назовём его «внутренность относительно аффинной оболочки $$A$$», то есть множество точек $$ri \, A := \{x \in X \, | \, \exists \varepsilon > 0: O(x, \, \varepsilon) \cap aff A \subset A\}$$.

Определение 4. (Отделимость в конечномерных пространствах). Пусть $$X$$ – конечномерное банахово пространство, множества $$A, \, B \subset X$$. Будем говорить, что множества $$A$$ и $$B$$ отделимы, если найдётся такой действующий на $$X$$ линейный непрерывный функционал $$l \not= 0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} Говорят также, что функционал $$l$$ разделяет множества $$A$$ и $$B$$.

Если, кроме того, оказалось, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right><\inf\limits_{y \in B}\left<l, y\right>, \end{gather*}

то говорят, что множества $$A$$ и $$B$$ строго отделимы.

Говорят также, что функционал $$l$$ строго разделяет множества $$A$$ и $$B$$.

Если вдобавок к вышесказанному оказалось, что существует число $$\delta > 0$$, для которого \begin{gather*} \left<l, x\right> + \delta < \left<l, y\right> \; \forall x \in A \, \forall y \in B, \end{gather*}

то говорят, что множества $$A$$ и $$B$$ сильно отделимы.

Говорят также, что функционал $$l$$ сильно разделяет множества $$A$$ и $$B$$.

Определение 5. (Отделимость в бесконечномерных пространствах). Пусть $$X$$ – бесконечномерное банахово пространство, множества $$A, \, B \subset X$$. Будем говорить, что множества $$A$$ и $$B$$ отделимы, если найдётся такой действующий на $$X$$ линейный функционал $$l \not= 0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*}

Говорят также, что функционал $$l$$ разделяет множества $$A$$ и $$B$$.

Если, кроме того, оказалось, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right><\inf\limits_{y \in B}\left<l, y\right>, \end{gather*}

то говорят, что множества $$A$$ и $$B$$ строго отделимы.

Говорят также, что функционал $$l$$ строго разделяет множества $$A$$ и $$B$$.

Если вдобавок к вышесказанному оказалось, что существует число $$\delta > 0$$, для которого \begin{gather*} \left<l, x\right> + \delta < \left<l, y\right> \; \forall x \in A \, \forall y \in B, \end{gather*}

то говорят, что множества $$A$$ и $$B$$ сильно отделимы.

Говорят также, что функционал $$l$$ сильно разделяет множества $$A$$ и $$B$$.

Это определение отличается от определения 4, ведь непрерывность функционала $$l$$ здесь не требуется. В определениях 4 и 5 не требуется выпуклость множеств $$A, \, B$$, однако утверждения ниже, как и другие результаты, касающиеся отделимости множеств, доказываются в предположении их выпуклости.

Определение 6. Пусть $$X$$ – банахово пространство. Функционал $$p: X \to \mathbb R$$ назовём однородно-выпуклым, если \begin{gather*} p(\lambda x) = \lambda x \; \forall \lambda \geqslant 0, \; p(x + y) \leqslant p(x) + p(y) \; \forall x, \, y \in X. \end{gather*}

Определение 7. Пусть $$X = (X, \, \left< \cdot, \, \cdot \right>)$$ – вещественное гильбертово пространство, число $$v \in \mathbb R$$, элемент $$p \in X, \, p \neq 0$$. Множество $$H_p := \{y \in X \, | \, \left< y, \, p \right> = v \}$$ – гиперплоскость в $$X$$.

Теоремы об отделимости в конечномерных пространствах

Начнём с важного результата в функциональном анализе - теоремы Хана-Банаха.

Теорема 1. (Hans Hahn, Stefan Banach). Пусть $$p$$ – однородно-выпуклый функционал на вещественном нормированном пространстве $$X$$. Пусть $$X_0 \subset X$$ – линейное подпространство, причём на $$X_0$$ задан линейный функционал $$f_0: X_0 \to \mathbb R$$, подчинённый функционалу $$p$$ (это означает, что $$f_0(x) \leqslant p(x) \; \forall x \in X_0$$). Тогда существует продолжение $$f$$ функционала $$f_0$$ с подпространства $$X_0$$ на всё пространство $$X$$, причём функционал $$f$$ подчинён функционалу $$p$$: \begin{gather*} f(x) \leqslant p(x) \; \forall x \in X. \end{gather*}

Доказательство. Доказательство этого классического утверждения можно найти, например, в [1].

Предложение 1. Множества $$A, \, B$$ можно отделить тогда и только тогда, когда множество $$A − B$$ (имеется в виду сумма по Минковскому множеств $$A$$ и $$-B$$, то есть множество $$\{a - b \, | \, a \in A, \, b \in B \}$$) можно отделить от $$\{0\}$$ (множества, состоящего из одного нуля).

Доказательство.

1. Необходимость. Пусть множества $$A, \, B$$ отделимы. Это означает, что $$\exists l \not= 0$$ – линейный непрерывный функционал на $$X$$ такой, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} То есть \begin{gather*} \forall x \in X \; \forall y \in Y \left<l, x\right> \leq \left<l, y\right>, \end{gather*} что означает: \begin{gather*} \forall x \in X \; \forall y \in Y \left<l, x - y\right> \leq 0 = \left<l, 0\right>, \end{gather*} или \begin{gather*} \sup_{z \in A - B} \left<l, z\right> \leq 0 = \inf_{z \in \{0\}} \left<l, z\right>. \end{gather*} Последнее неравенство эквивалентно отделимости множества $$A - B$$ от множества $$\{0\}$$.

2. Достаточность. Пусть множество $$A - B$$ отделимо от нуля. Тогда $$\exists l \not= 0$$ – линейный непрерывный функционал на $$X$$ такой, что \begin{gather*} \sup_{z \in A - B} \left<l, z\right> \leq 0 = \left<l, 0\right>, \end{gather*} и поскольку \begin{gather*} \displaystyle \sup_{z \in (A - B)} \left< l, \, z \right> = \sup_{a \in A, \, b \in B} \left< l, \, a - b \right> = \sup_{a \in A, \, b \in B} (\left< l, \, a \right> - \left<l, \, b \right>) = \sup_{a \in A} \left< l, \, a \right> - \inf_{b \in B} \left< l, \, b \right>, \end{gather*}

то заключаем \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{y \in B}\left<l, y\right>. \end{gather*} Последнее неравенство эквивалентно отделимости множеств $$A$$ и $$B$$. $$~~\blacksquare$$

Этим фактом мы воспользуемся при доказательстве следующей теоремы. Далее в этом разделе, не уменьшая общности, будем считать конечномерное пространство евклидовым: $$X = \mathbb R ^ n$$. Предпошлем доказательству теоремы одну лемму.

Лемма 1. Пусть непустое множество $$C \subset \mathbb R ^ n$$ выпукло, причём $$0 \not \in int \, C$$. Тогда $$C$$ отделимо от нуля.

Доказательство. Рассмотрим выпуклое замкнутое множество $$\overline C$$. Понятно, что нуль не принадлежит внутренности $$int \, \overline C$$, поскольку $$int \, C = int \, \overline C$$. Поэтому либо нуль не принадлежит множеству $$\overline C$$, либо принадлежит его границе $$\partial \overline C$$. Значит, в любом случае существует последовательность $$x_i \to 0, \, x_i \not \in \overline C \, \forall i$$. Рассмотрим множества $$C_i := \overline C - x_i$$ (имеется в виду сумма по Минковскому множеств $$\overline C$$ и $$\{-x_i\}$$). Имеем $$0 \not \in C_i \; \forall i$$. Каждое из этих непустых выпуклых замкнутых множеств $$C_i$$ можно отделить от нуля. Следовательно, для любого $$i$$ существуют числа $$l_i \in \mathbb R$$ такие, что $$\left< l_i, \eta \right> \geqslant 0 \; \forall \eta \in C_i$$. Нормируем каждый вектор $$l_i$$. Тогда все эти векторы единичные. Перейдём, пользуясь теоремой Больцано-Вейерштрасса, от ограниченной последовательности $$\{l_i\}$$ к сходящейся подпоследовательности $$\{l_{i_k}\}$$, обозначим $$l = \displaystyle \lim_{k \to +\infty} l_{i_k}, \, l \not= 0$$. Заметим, что для любого элемента $$x \in \overline C$$ и для любого номера $$i \in \mathbb N$$ существует $$y = y(x, \, i) \in C_i: x = x_i + y$$, поскольку $$C_i = C - x_i = \{z - x_i \, | \, z \in \overline C\}$$. Поэтому $$\left< l_i, x \right> = \left< l_i, x_i + y \right> = \left< l_i, x_i \right> + \left< l_i, y \right> \geqslant \left< l_i, x_i \right>$$ (ведь $$y \in C_i$$). По неравенству Коши-Буняковского, $$\left< l_i, x_i \right> \geqslant -|l_i| |x_i|$$, и значит, \begin{equation} \label{eq1} \left< l_i, x \right> + |l_i| |x_i| \geqslant 0 \, \forall x \in \overline C \; \forall i. \end{equation} Зафиксируем $$x \in \overline C$$, и, переходя в полученных неравенствах $$\eqref{eq1}$$ к пределу при $$i \to +\infty$$, получим $$\left< l, x \right> \geqslant 0$$. В силу произвольности выбора $$x$$ мы получаем, что $$C$$ отделимо от нуля. $$~~\blacksquare$$

Теорема 2. (Об отделимости в конечномерном пространстве). Пусть $$A, B$$ – непустые выпуклые подмножества $$\mathbb R^n$$ и их относительные внутренности $$ri \, A$$ и $$ri \, B$$ не пересекаются. Тогда множества $$A$$ и $$B$$ можно отделить.

Доказательство. Заметим, что так как $$ri \, A \cap ri \, B = \emptyset$$, то $$0\not\in (ri \, A - ri \, B)$$. Множество $$(ri \, A - ri \, B)$$ выпукло, значит, $$(ri \, A - ri \, B)$$ отделимо от нуля в силу Леммы 1, а значит, множества $$ri \, A$$ и $$ri \, B$$ отделимы, то есть на $$X$$ существует линейный непрерывный функционал $$l \not= 0$$ и число $$\gamma \in \mathbb R: \forall x \in {ri \, A} \; \forall y \in {ri \, B} \Longrightarrow\left<l, x\right>\leq\gamma\leq\left<l, y\right>$$.

Пусть точка $$x \in A$$. Тогда существует последовательность точек $$\{x_i\}$$, лежащая в $$ri A$$ и сходящаяся к $$x$$. Поэтому $$\left<l, x_i\right>\leq\gamma \; \forall i$$. Переходя к пределу при $$i \to \infty$$ получаем, что $$\left<l, x\right>\leq\gamma$$. Поступив аналогично для точек $$y$$ множества $$B$$, получим, что линейный непрерывный функционал $$l$$ также разделяет множества $$A$$ и $$B$$.$$~~\blacksquare$$

Теоремы об отделимости в бесконечномерных пространствах

Теперь перейдём к бесконечномерному пространству $$X$$. Отделимость множеств в $$X$$ имеет отличия от отделимости множеств в $$\mathbb R ^ n$$, что показывает следующий пример.

Пример 1. В бесконечномерном пространстве $$l_2$$ числовых последовательностей $$(x_1, \, x_2, \, \ldots, \, x_n, \, \ldots)$$, для которых ряд $$\displaystyle \sum_{i = 1} ^ {+\infty} x_i ^ 2 < \infty$$, рассмотрим множество \begin{gather*} П = \{x = (x_1, \, x_2, \, \ldots, \, x_n, \, \ldots) \, | \, |x_i| \leqslant 2 ^ {-i} \, \forall i \}, \end{gather*}

называемое гильбертовым кирпичом. Это множество таково:

1. П содержит нуль (проверяется подстановкой последовательности $$(0, \, 0, \, \ldots, \, 0, \, \ldots)$$ в определение П);
2. П является выпуклым компактом;
3. П не лежит ни в каком конечномерном пространстве;
4. $$int$$ П не содержит нуля.

Докажем последнее свойство. Предположим противное: пусть $$0 \in int$$ П. Тогда $$\exists \varepsilon > 0: B(0, \, \varepsilon) \subset$$ П. Выберем число $$j = \Big \lfloor \log_2 \displaystyle \frac{1}{\varepsilon} \Big \rfloor + 1$$. Тогда $$2 ^ {-j} < 2 ^ {-\log_2 \frac{1}{\varepsilon}} = \varepsilon$$. Но последовательность $$y = (0, \, 0, \, \ldots, \, \varepsilon, \, \ldots)$$, где компонента $$\varepsilon$$ – с номером $$j$$, имеет норму $$||y|| = \sqrt{\displaystyle \sum_{i = 1} ^ {+\infty} y_i ^ 2} = \varepsilon \Rightarrow y \in B(0, \, \varepsilon) \subset$$ П, однако $$y \not \in$$ П, ведь $$|y_j| = \varepsilon > 2 ^ {-j}$$. Полученное противоречие доказывает, что $$int$$ П не содержит нуля.

Докажем, что П не отделено от множества $$\{ 0 \}$$. В конечномерном пространстве П было бы отделено от $$\{0\}$$ в силу Леммы 1, так как оно выпуклое и его внутренность не содержит нуля. Предположим противное: пусть множества П и $$\{0\}$$ отделимы. Тогда существует разделяющий их ненулевой линейный функционал $$l$$, действующий на пространстве $$l_2$$. Имеем \begin{equation} \label{eq2} \left< l, \, x \right> \leqslant 0 \; \forall x \in П. \end{equation} Рассмотрим две последовательности векторов $$e_i ^ {+} = (0, \, 0, \, \ldots, \, 0, \, 2 ^ {-i}, \, 0, \, \ldots)$$ и $$e_i ^ {-} = (0, \, 0, \, \ldots, \, 0, \, -2 ^ {-i}, \, 0, \, \ldots)$$, где $$i \in \mathbb N$$, а единственная ненулевая компонента векторов $$e_i ^ {+}, \, e_i ^ {-}$$ имеет номер $$i$$. Все эти векторы $$e_i ^ {+}, \, e_i ^ {-}$$ принадлежат П. Подставим векторы из этой последовательности в $$\eqref{eq2}$$. Видим, что из $$\left< l, \, e_i ^ {+} \right> = l_i 2 ^ {-i} \geqslant 0, \, \left< l, \, e_i ^ {-} \right> = -l_i 2 ^ {-i} \geqslant 0$$ следует $$l_i = 0 \; \forall i$$, и значит $$l = 0$$. Противоречие с условием $$l \neq 0$$.

Значит, множества П и $$\{0\}$$ не отделимы. $$~~\blacksquare$$

Замечание. Как известно из курса функционального анализа, действие функционала $$l \in l_2 ^ {*}$$ на элемент $$x = (x_1, \, x_2, \, \ldots) \in l_2$$ (под $$l_2 ^ {*}$$ имеется в виду сопряжённое к $$l_2$$ пространство, состоящее из линейных ограниченных функционалов, действующих на $$l_2$$) может быть формально записано так: $$l(x) = \left< l, \, x \right> = l_1 x_1 + l_2 x_2 + \ldots$$, где числа $$l_i$$ определяют функционал $$l$$.

Сформулируем достаточные условия отделимости и строгой отделимости множеств в бесконечномерном пространстве.

Теорема 3. (Об отделимости в бесконечномерном пространстве). Пусть $$M, \, N$$ – непустые выпуклые подмножества $$X, \, int \, M \not= \emptyset$$ и $$int \, M \cap N = \emptyset$$. Тогда множества $$M$$ и $$N$$ можно отделить.

Теорема 4. (О строгой отделимости в бесконечномерном пространстве). Пусть $$A, \, B$$ – непустые выпуклые подмножества $$X, \, A \cap B = \emptyset, \; A$$ компактно, а $$B$$ замкнуто. Тогда множества $$A$$ и $$B$$ можно строго отделить.

Список литературы

1. Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1989.

2. Арутюнов А.В. Лекции по выпуклому и многозначному анализу. М.: ФИЗМАТЛИТ, 2014.

3. Половинкин Е.С., Балашов М.В. Элементы выпуклого и сильно выпуклого анализа. М.: ФИЗМАТЛИТ, 2007.