Логистическое уравнение и его свойства: различия между версиями
Kirill23 (обсуждение | вклад) |
Kirill23 (обсуждение | вклад) |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
Логистическое уравнение — уравнение, описывающее численность изолированной популяции в момент времени $$t$$ и имеющее вид | Логистическое уравнение — уравнение, описывающее численность изолированной популяции в момент времени $$t$$ и имеющее вид | ||
| + | \begin{equation} | ||
\label{eq1} | \label{eq1} | ||
| − | |||
\dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right) , | \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right) , | ||
\end{equation} | \end{equation} | ||
| Строка 53: | Строка 53: | ||
Найдем $$ C $$ из начального условия $$ N(0) = N_0: \ C = 1 - \frac{K}{N_0}. $$ Окончательно получим | Найдем $$ C $$ из начального условия $$ N(0) = N_0: \ C = 1 - \frac{K}{N_0}. $$ Окончательно получим | ||
| + | \begin{equation} | ||
\label{eq2} | \label{eq2} | ||
| − | |||
N(t) = \dfrac{K}{1 - \left( 1 - \frac{K}{N_0} \right) e^{-rt} } = \dfrac{K e^{rt} }{e^{rt} - 1 + \frac{K}{N_0}} = | N(t) = \dfrac{K}{1 - \left( 1 - \frac{K}{N_0} \right) e^{-rt} } = \dfrac{K e^{rt} }{e^{rt} - 1 + \frac{K}{N_0}} = | ||
\dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . | \dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . | ||
| Строка 81: | Строка 81: | ||
Это уравнение можно получить, используя явную схему дискретизации для логистического уравнения, т.е. заменяя производную по времени на разность | Это уравнение можно получить, используя явную схему дискретизации для логистического уравнения, т.е. заменяя производную по времени на разность | ||
| − | $$ \dot N = \frac{\Delta N}{\Delta t} $$, где $$ \Delta N = N_{t + \Delta t} - N_t$$ . Если мы положим $$ \Delta t = 1 $$, то получим из ( | + | $$ \dot N = \frac{\Delta N}{\Delta t} $$, где $$ \Delta N = N_{t + \Delta t} - N_t$$ . Если мы положим $$ \Delta t = 1 $$, то получим из (\ref{eq1}), что |
\[ N_{t+1} = N_{t} + r N_t \left( 1 - \dfrac{N_t}{K} \right) , \] | \[ N_{t+1} = N_{t} + r N_t \left( 1 - \dfrac{N_t}{K} \right) , \] | ||
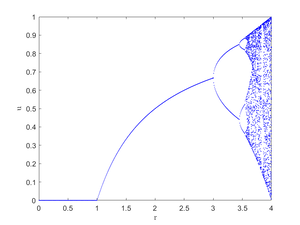
[[Файл:For before diplom6.png|мини|справа|Бифуркационная диаграмма логистического уравнения при $$u_0 = 0.3$$.]] | [[Файл:For before diplom6.png|мини|справа|Бифуркационная диаграмма логистического уравнения при $$u_0 = 0.3$$.]] | ||
| − | от которого с помощью очевидных переобозначений можно перейти к | + | от которого с помощью очевидных переобозначений можно перейти к дискретному логистическому уравнению. |
Сделав замену $$ N_t = K u_t $$, уравнение (\ref{eq3}) приводится к виду: | Сделав замену $$ N_t = K u_t $$, уравнение (\ref{eq3}) приводится к виду: | ||
| + | \begin{equation} | ||
\label{eq4} | \label{eq4} | ||
| − | |||
u_{t+1} = r u_t (1 - u_t) , \ r > 0 , \ 0 \leq u_t < 1 . | u_{t+1} = r u_t (1 - u_t) , \ r > 0 , \ 0 \leq u_t < 1 . | ||
\end{equation} | \end{equation} | ||
Текущая версия на 02:27, 17 декабря 2023
Логистическое уравнение — уравнение, описывающее численность изолированной популяции в момент времени $$t$$ и имеющее вид \begin{equation} \label{eq1} \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right) , \end{equation}
где $$r, K$$ — положительные параметры модели.
Содержание
История возникновения
Пусть $$ N(t) $$ — численность изолированной популяции в момент времени $$ t $$. Скорость её изменения может быть представлена в следующем виде
\[ \dot N = \text{рождаемость} - \text{смертность} + \text{миграция} . \]
Вид различных членов в правой части этого уравнения зависит от конкретных условий существования популяций и присущих ей свойств. В простейшем случае предполагается отсутствие миграции, а члены рождаемости и смертности пропорциональны общей численности популяции $$ N $$:
\[ \dot N = bN - cN, \ \ \ \ \ \ \ \Rightarrow \ \ \ \ \ \ \ \dot N = aN, \ a = b - c .\]
Поскольку в действительности наблюдаются стабильные популяции, то необходимо рассматривать математические модели, в которых плотность популяции играет регулирующую роль. Очевидно, что коэффициент размножения в такой модели должен быть не постоянным, а зависящим от численности или плотности. Более точно, математическая модель роста замкнутой популяции имеет вид
\[ \dot N = N \cdot f(N) , \]
где $$ f(N) $$ — коэффициент скорости роста популяции. Разложим $$ f(N) $$ в ряд Тейлора в окрестности нуля и отбросим все члены, кроме первых двух. Получим
\[ \dot N = N(d + eN), \]
где $$ d,e $$ — некоторые постоянные, причем естественно предположить, что $$ d > 0, \ e < 0 $$. Именно таким образом Альфред Лотка пришел к динамической системе, которое стало известно как логистическое уравнение, которое после некоторых переобозначений запишется в виде:
\[ \dot N = rN \left( 1 - \dfrac{N}{K} \right) . \]
Здесь $$ r $$ и $$K$$ — положительные параметры.
Решение уравнения
Можно заметить, что когда $$ N(t) $$ мало, то $$ \dot N \approx rN $$. Значит, $$N$$ экспоненциально растёт. Параметр $$ K $$ интерпретируется как потенциальная емкость экологической системы, которая определяется доступным наличным количеством ресурсов. Величина $$ K $$ определяет предельное значение численности популяции. Для доказательства этого факта решим логистическое уравнение:
\[ \dfrac{dN}{dt} = rN \left( 1 - \dfrac{N}{K} \right), \]
\[ -\dfrac{1}{r} \int \dfrac{dN}{\frac{N^2}{K} - N} = \int dt , \]
Сделаем замену в правой части равенства: $$ z = \frac{N}{\sqrt{K}} - \frac{1}{2} \sqrt{k}, \ dz = \frac{dN}{\sqrt{k}} $$. Получим
\[ - \dfrac{\sqrt{K}}{r} \int \dfrac{dz}{z^2 - \frac{1}{4} k} = \int dt , \]
\[ -\dfrac{1}{r} \ln{ \left| \dfrac{z - \frac{1}{2} \sqrt{k} }{z + \frac{1}{2} \sqrt{k}} \right| } = t + C , \]
\[ \dfrac{z - \frac{1}{2} \sqrt{k} }{z + \frac{1}{2} \sqrt{k}} = Ce^{-rt} . \]
Возвращаясь к $$N$$, получим
\[ N = \dfrac{K}{1 - Ce^{-rt}}. \]
Найдем $$ C $$ из начального условия $$ N(0) = N_0: \ C = 1 - \frac{K}{N_0}. $$ Окончательно получим
\begin{equation} \label{eq2} N(t) = \dfrac{K}{1 - \left( 1 - \frac{K}{N_0} \right) e^{-rt} } = \dfrac{K e^{rt} }{e^{rt} - 1 + \frac{K}{N_0}} = \dfrac{N_0 K e^{rt}}{N_0 (e^{rt} - 1) + K} . \end{equation}
Свойства
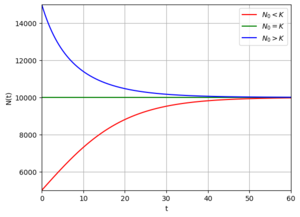
Это решение для $$ 0 < N_0 < K $$ представляет собой сигмоидальную кривую, которая также часто называют логистической кривой
Таким образом, $$ N(t) \rightarrow K$$ при $$ t \rightarrow +\infty $$. Тем самым, величина $$ K$$ определяет финальное состояние численности популяции.
Очевидно, что логистическое уравнение не следует воспринимать буквально как уравнение, управляющее популяционной динамикой реальных систем (например, критику логистического закона роста можно найти в статье автора классического учебника по теории вероятностей В. Феллера [3]). Наиболее правильным представляется использование логистического уравнения как самой простой и удобной формы описания популяции, численность которой стремится к некоторой конечной фиксированной величине. Логистическое уравнение — это первое приближение к описанию численности популяции с плотностно-зависимым регуляторным механизмом, на динамику которой влияют эффекты перенаселения и ограниченности ресурсов. Существенным недостатком модели является тот факт, что предельная численность популяции вводится в качестве известного параметра, в то время как отыскание этой величины нередко является основной задачей исследования.
Дискретное логистическое уравнение
Рассмотрим теперь дискретный вариант логистического уравнения, которое имеет вид
\begin{equation} \label{eq3} N_{t+1} = r N_t \left( 1 - \dfrac{N_t}{K} \right) , \ \ \ r, K > 0 . \end{equation}
Это уравнение можно получить, используя явную схему дискретизации для логистического уравнения, т.е. заменяя производную по времени на разность $$ \dot N = \frac{\Delta N}{\Delta t} $$, где $$ \Delta N = N_{t + \Delta t} - N_t$$ . Если мы положим $$ \Delta t = 1 $$, то получим из (\ref{eq1}), что
\[ N_{t+1} = N_{t} + r N_t \left( 1 - \dfrac{N_t}{K} \right) , \]
от которого с помощью очевидных переобозначений можно перейти к дискретному логистическому уравнению. Сделав замену $$ N_t = K u_t $$, уравнение (\ref{eq3}) приводится к виду:
\begin{equation} \label{eq4} u_{t+1} = r u_t (1 - u_t) , \ r > 0 , \ 0 \leq u_t < 1 . \end{equation}
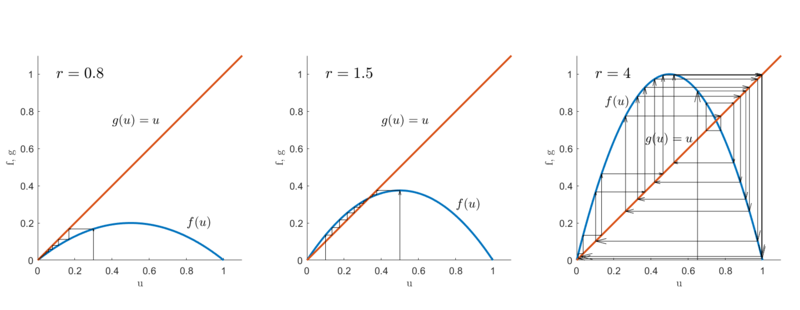
Обозначим $$f(u) = r u_t (1 - u_t)$$. Найдём неподвижные точки, приравняв правую часть уравнения к 0: $$ u_1^* = 0, u_2^* = \frac{r-1}{r} $$. Исследуем неподвижные точки на устойчивость. Так как нас интересуют только неотрицательные решения, то вторая неподвижная точка существует лишь в случае $$ r > 1 $$. Далее имеем, $$ f_u (u) = r - 2ru, \ f_u(u_1^*) = r$$, следовательно, точка $$ u_1^* $$ асимптотически устойчива, если $$ 0 < r < 1 $$, и неустойчива, если $$r > 1$$. Если $$r = 1$$, то $$ f_u(u_1^*) = 1$$. Пусть $$ r > 1 $$, тогда существует вторая неподвижная точка, для которой $$f_u(u_2^*) = 2 - r$$. Следовательно, точка $$u_2^*$$ устойчива, если $$ 1 < r < 3 $$, и неустойчива, если $$r > 3$$. Если $$r = 3$$, то $$f_u(u_2^*) = -1$$.
Построим бифуркационную диаграмму. Для этого фиксируем начальное значение $$u_0$$ и для каждого значения параметра $$r$$ на выбранном интервале будем выводить на график значения $$u_t$$ для больших $$t$$. Исходя из бифуркационной диаграммы, при $$r < 1$$ траектория нашей дискретного логистического уравнения сходится к точке $$u_1^*$$. При $$ 1 < r < 3 $$ траектория сходится ко второй особой точке $$u_2^* = \frac{r-1}{r}$$. Далее появляется цикл длины 2, который затем превращается в цикл длины 4, а дальше и вовсе начинается хаос.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.
3. Feller W. On the Logistic Law of Growth and Its Empirical Verification in Biology, Acta Biotheoretica, 5, 1940, 51–65.