Топологически орбитально эквивалентные системы: различия между версиями
Kirill24 (обсуждение | вклад) (Полностью удалено содержимое страницы) Метка: очистка |
Kirill24 (обсуждение | вклад) |
||
| (не показаны 44 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
| + | Рассмотрим две [https://sawiki.cs.msu.ru/index.php/Динамическая_система динамические системы] с непрерывным временем | ||
| + | \begin{align}\label{sys1} | ||
| + | \dot{u} = g(u), \quad u \in \mathbb{R}^n,\\ | ||
| + | \label{sys2} | ||
| + | \dot{v} = f(v), \quad v \in \mathbb{R}^n, | ||
| + | \end{align} | ||
| + | где $$g(u) = (g_1(u), g_2(u), \dots, g_n(u)), f(v) = (f_1(v), f_2(v), \dots, f_n(v)).$$ | ||
| + | |||
| + | Пусть функции $$f(\cdot)$$ и $$g(\cdot)$$ связаны соотношением | ||
| + | \begin{equation} \label{func_dep} | ||
| + | g(u) = \mu(u)f(u), \forall u \in U \subset \mathbb{R}^n, | ||
| + | \end{equation} | ||
| + | где $$\mu(\cdot)$$ — гладкая скалярная положительная для всех $$u \in U$$ функция. | ||
| + | |||
| + | Системы \eqref{sys1} и \eqref{sys2}, правые части которых связаны соотношением \eqref{func_dep}, называются '''орбитально эквивалентными''' в области $$U$$. | ||
| + | |||
| + | __TOC__ | ||
| + | |||
| + | =Свойства орбитально эквивалентных систем= | ||
| + | '''Утверждение.''' | ||
| + | Орбитально эквивалентные системы в области $$U$$ являются [https://ru.wikipedia.org/wiki/Орбитально-топологическая_эквивалентность топологически эквивалентными] в этой области. | ||
| + | |||
| + | '''Доказательство.''' | ||
| + | Особые точки систем \eqref{sys1} и \eqref{sys2} являются корнями уравнений: | ||
| + | \begin{align*} | ||
| + | f(u) = 0,\\ | ||
| + | g(u) = 0. | ||
| + | \end{align*} | ||
| + | |||
| + | Поскольку $$\mu(u) > 0, \forall u \in U,$$ то корни уравнений совпадают. | ||
| + | |||
| + | Далее для простоты будем считать, что $$n = 2$$, т.к. доказательство легко обобщается на случай произвольного $$n$$. | ||
| + | |||
| + | Найдем [https://sawiki.cs.msu.ru/index.php/Матрица_Якоби._Лемма_о_выпрямлении_векторного_поля матрицу Якоби] системы \eqref{sys1}. | ||
| + | |||
| + | \begin{equation*} | ||
| + | J_1(u_1, u_2) = \left.\left[\dfrac{\partial g}{\partial u}\right]\right|_{(u_1, u_2)} = | ||
| + | \left.\left[\dfrac{\partial (\mu f)}{\partial u}\right]\right|_{(u_1, u_2)} = | ||
| + | \left.\begin{pmatrix} | ||
| + | \dfrac{\partial \mu}{\partial u_1}f_1 | ||
| + | + \dfrac{\partial f_1}{\partial u_1}\mu & | ||
| + | \dfrac{\partial \mu}{\partial u_2}f_1 | ||
| + | + \dfrac{\partial f_1}{\partial u_2}\mu\\ | ||
| + | \dfrac{\partial \mu}{\partial u_1}f_2 | ||
| + | + \dfrac{\partial f_2}{\partial u_1}\mu & | ||
| + | \dfrac{\partial \mu}{\partial u_2}f_2 | ||
| + | + \dfrac{\partial f_2}{\partial u_2}\mu | ||
| + | \end{pmatrix}\right|_{(u_1,u_2)}. | ||
| + | \end{equation*} | ||
| + | |||
| + | Если точка $$(u_1, u_2)$$ является особой, то $$f_1(u_1, u_2) = f_2(u_1, u_2) = 0.$$ Тогда матрица Якоби системы \eqref{sys1} равна | ||
| + | |||
| + | \begin{equation*} | ||
| + | J_1(u_1, u_2) = | ||
| + | \left.\begin{pmatrix} | ||
| + | \dfrac{\partial f_1}{\partial u_1}\mu & | ||
| + | \dfrac{\partial f_1}{\partial u_2}\mu\\ | ||
| + | \dfrac{\partial f_2}{\partial u_1}\mu & | ||
| + | \dfrac{\partial f_2}{\partial u_2}\mu | ||
| + | \end{pmatrix}\right|_{(u_1,u_2)} = | ||
| + | (\mu(u_1, u_2))^2 | ||
| + | \left.\begin{pmatrix} | ||
| + | \dfrac{\partial f_1}{\partial u_1} & | ||
| + | \dfrac{\partial f_1}{\partial u_2}\\ | ||
| + | \dfrac{\partial f_2}{\partial u_1} & | ||
| + | \dfrac{\partial f_2}{\partial u_2} | ||
| + | \end{pmatrix}\right|_{(u_1,u_2)} = (\mu(u_1, u_2))^2 J_2(u_1,u_2), | ||
| + | \end{equation*} | ||
| + | |||
| + | где $$J_2(u_1, u_2)$$ — матрица Якоби системы \eqref{sys2}. Поскольку $$\mu(u_1, u_2) > 0$$, то знаки собственных значений матриц Якоби систем \eqref{sys1} и \eqref{sys2} одинаковы. Поэтому особые точки имеют одинаковый характер устойчивости. Значит, системы \eqref{sys1} и \eqref{sys2} топологически эквивалентны. | ||
| + | |||
| + | Таким образом, орбитально эквивалентные системы являются топологически эквивалентными, поэтому их называют '''топологически орбитально''' эквивалентными. | ||
| + | |||
| + | '''Замечание.''' Можно понимать орбитальную эквивалентность как нелинейную деформацию времени. Так, если в системе \eqref{sys1} сделать замену $$t = \mu(u)\tau, \operatorname{d}t = \mu(u)\operatorname{d}\tau,$$ то получим систему \eqref{sys2}. Таким образом, траектории орбитально эквивалентных систем отличаются лишь скоростью прохождения по ним. | ||
| + | |||
| + | '''Утверждение.''' | ||
| + | Если в области $$U$$ выполнено неравенство $$\dfrac{\partial (\mu f_1)}{\partial u_1} +\dfrac{\partial (\mu f_2)}{\partial u_2} > 0 ($$или $$< 0),$$ | ||
| + | то в ней нет замкнутых траекторий системы \eqref{sys1}. | ||
| + | |||
| + | '''Доказательство.''' | ||
| + | Заметим, что левая часть указанного неравенства есть дивергенция правой части системы \eqref{sys1} $$\implies$$ по теореме [https://sawiki.cs.msu.ru/index.php/Предельное_поведение_траекторий._Предельные_циклы._Теорема_Дюлака-Бендиксона Дюлака-Бендиксона] в области $$U$$ нет замкнутых траекторий системы. | ||
| + | |||
| + | =Пример= | ||
| + | Рассмотрим две системы: | ||
| + | \begin{equation} | ||
| + | \begin{cases}\label{first_sys_1} | ||
| + | \dot{x}_1 = x_2(1-(x_1^2+x_2^2)),\\ | ||
| + | \dot{x}_2 = -x_1(1-(x_1^2+x_2^2)) | ||
| + | \end{cases}\\ | ||
| + | \end{equation} | ||
| + | \begin{equation} | ||
| + | \begin{cases}\label{second_sys_1} | ||
| + | \dot{x}_1 = x_2,\\ | ||
| + | \dot{x}_2 = -x_1 | ||
| + | \end{cases} | ||
| + | \end{equation} | ||
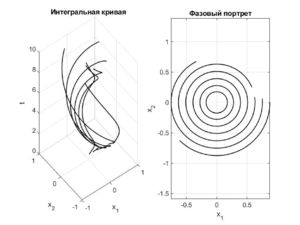
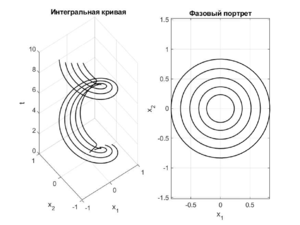
| + | Эти системы топологически орбитально эквивалентны в области $$U = \{(x_1,x_2)\mid x_1^2 + x_2^2 < 1\}.$$ Смотря на интегральные кривые, можно заметить, что скорость прохождения по траекториям системы \eqref{first_sys_1} меньше, чем скорость прохождения по траекториям системы \eqref{second_sys_1}. | ||
| + | [[Файл:First_sys_1.png|мини|Интегральная кривая и фазовый портрет системы \eqref{first_sys_1} в области $$U$$]] | ||
| + | [[Файл:Second_sys_1.png|мини|Интегральная кривая и фазовый портрет системы \eqref{second_sys_1} в области $$U$$]] | ||
| + | |||
| + | = Список литературы = | ||
| + | # Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2024. | ||
| + | # Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011. | ||
Текущая версия на 21:10, 8 декабря 2024
Рассмотрим две динамические системы с непрерывным временем \begin{align}\label{sys1} \dot{u} = g(u), \quad u \in \mathbb{R}^n,\\ \label{sys2} \dot{v} = f(v), \quad v \in \mathbb{R}^n, \end{align} где $$g(u) = (g_1(u), g_2(u), \dots, g_n(u)), f(v) = (f_1(v), f_2(v), \dots, f_n(v)).$$
Пусть функции $$f(\cdot)$$ и $$g(\cdot)$$ связаны соотношением \begin{equation} \label{func_dep} g(u) = \mu(u)f(u), \forall u \in U \subset \mathbb{R}^n, \end{equation} где $$\mu(\cdot)$$ — гладкая скалярная положительная для всех $$u \in U$$ функция.
Системы \eqref{sys1} и \eqref{sys2}, правые части которых связаны соотношением \eqref{func_dep}, называются орбитально эквивалентными в области $$U$$.
Свойства орбитально эквивалентных систем
Утверждение. Орбитально эквивалентные системы в области $$U$$ являются топологически эквивалентными в этой области.
Доказательство. Особые точки систем \eqref{sys1} и \eqref{sys2} являются корнями уравнений: \begin{align*} f(u) = 0,\\ g(u) = 0. \end{align*}
Поскольку $$\mu(u) > 0, \forall u \in U,$$ то корни уравнений совпадают.
Далее для простоты будем считать, что $$n = 2$$, т.к. доказательство легко обобщается на случай произвольного $$n$$.
Найдем матрицу Якоби системы \eqref{sys1}.
\begin{equation*} J_1(u_1, u_2) = \left.\left[\dfrac{\partial g}{\partial u}\right]\right|_{(u_1, u_2)} = \left.\left[\dfrac{\partial (\mu f)}{\partial u}\right]\right|_{(u_1, u_2)} = \left.\begin{pmatrix} \dfrac{\partial \mu}{\partial u_1}f_1 + \dfrac{\partial f_1}{\partial u_1}\mu & \dfrac{\partial \mu}{\partial u_2}f_1 + \dfrac{\partial f_1}{\partial u_2}\mu\\ \dfrac{\partial \mu}{\partial u_1}f_2 + \dfrac{\partial f_2}{\partial u_1}\mu & \dfrac{\partial \mu}{\partial u_2}f_2 + \dfrac{\partial f_2}{\partial u_2}\mu \end{pmatrix}\right|_{(u_1,u_2)}. \end{equation*}
Если точка $$(u_1, u_2)$$ является особой, то $$f_1(u_1, u_2) = f_2(u_1, u_2) = 0.$$ Тогда матрица Якоби системы \eqref{sys1} равна
\begin{equation*} J_1(u_1, u_2) = \left.\begin{pmatrix} \dfrac{\partial f_1}{\partial u_1}\mu & \dfrac{\partial f_1}{\partial u_2}\mu\\ \dfrac{\partial f_2}{\partial u_1}\mu & \dfrac{\partial f_2}{\partial u_2}\mu \end{pmatrix}\right|_{(u_1,u_2)} = (\mu(u_1, u_2))^2 \left.\begin{pmatrix} \dfrac{\partial f_1}{\partial u_1} & \dfrac{\partial f_1}{\partial u_2}\\ \dfrac{\partial f_2}{\partial u_1} & \dfrac{\partial f_2}{\partial u_2} \end{pmatrix}\right|_{(u_1,u_2)} = (\mu(u_1, u_2))^2 J_2(u_1,u_2), \end{equation*}
где $$J_2(u_1, u_2)$$ — матрица Якоби системы \eqref{sys2}. Поскольку $$\mu(u_1, u_2) > 0$$, то знаки собственных значений матриц Якоби систем \eqref{sys1} и \eqref{sys2} одинаковы. Поэтому особые точки имеют одинаковый характер устойчивости. Значит, системы \eqref{sys1} и \eqref{sys2} топологически эквивалентны.
Таким образом, орбитально эквивалентные системы являются топологически эквивалентными, поэтому их называют топологически орбитально эквивалентными.
Замечание. Можно понимать орбитальную эквивалентность как нелинейную деформацию времени. Так, если в системе \eqref{sys1} сделать замену $$t = \mu(u)\tau, \operatorname{d}t = \mu(u)\operatorname{d}\tau,$$ то получим систему \eqref{sys2}. Таким образом, траектории орбитально эквивалентных систем отличаются лишь скоростью прохождения по ним.
Утверждение. Если в области $$U$$ выполнено неравенство $$\dfrac{\partial (\mu f_1)}{\partial u_1} +\dfrac{\partial (\mu f_2)}{\partial u_2} > 0 ($$или $$< 0),$$ то в ней нет замкнутых траекторий системы \eqref{sys1}.
Доказательство. Заметим, что левая часть указанного неравенства есть дивергенция правой части системы \eqref{sys1} $$\implies$$ по теореме Дюлака-Бендиксона в области $$U$$ нет замкнутых траекторий системы.
Пример
Рассмотрим две системы: \begin{equation} \begin{cases}\label{first_sys_1} \dot{x}_1 = x_2(1-(x_1^2+x_2^2)),\\ \dot{x}_2 = -x_1(1-(x_1^2+x_2^2)) \end{cases}\\ \end{equation} \begin{equation} \begin{cases}\label{second_sys_1} \dot{x}_1 = x_2,\\ \dot{x}_2 = -x_1 \end{cases} \end{equation} Эти системы топологически орбитально эквивалентны в области $$U = \{(x_1,x_2)\mid x_1^2 + x_2^2 < 1\}.$$ Смотря на интегральные кривые, можно заметить, что скорость прохождения по траекториям системы \eqref{first_sys_1} меньше, чем скорость прохождения по траекториям системы \eqref{second_sys_1}.
Список литературы
- Абрамова В.В. "Лекции по динамическим системам и биоматематике", 2024.
- Братусь А.С., Новожилов А.С., Платонов А.П. "Динамические системы и модели биологии", 2011.