Опорная функция множества: различия между версиями
Igor (обсуждение | вклад) |
Igor (обсуждение | вклад) |
||
| Строка 3: | Строка 3: | ||
== Определение и интерпретация == | == Определение и интерпретация == | ||
| + | |||
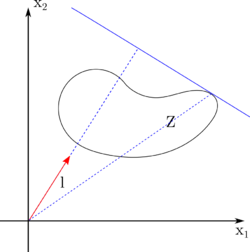
| + | [[File:Support_func.png|thumb|250px|Опорная функция множества]] | ||
Пусть $$Z \subseteq \mathbb{R}^n$$, тогда '''опорной функцией множества $$Z$$''' будем называть функцию $$\rho(\cdot \mid Z) \colon\ \mathbb{R}^n \mapsto \mathbb{R} \cup \{ \pm \infty \}$$, такую что: | Пусть $$Z \subseteq \mathbb{R}^n$$, тогда '''опорной функцией множества $$Z$$''' будем называть функцию $$\rho(\cdot \mid Z) \colon\ \mathbb{R}^n \mapsto \mathbb{R} \cup \{ \pm \infty \}$$, такую что: | ||
| Строка 11: | Строка 13: | ||
\end{cases} | \end{cases} | ||
\] | \] | ||
| + | |||
| + | Опорная функция имеет достаточно простую геометрическую интерпретацию. | ||
| + | Рассмотрим множество $$Z$$ на плоскости и некоторое направление $$l$$. | ||
| + | Для простоты положим $$\| l \| = 1$$. Тогда опорной функций множества $$Z$$ в направлении $$l$$ будет расстояние (со знаком!) от начала координат до точки множества, наиболее удаленной в данном направлении. | ||
| + | То есть мы начинаем отодвигать гиперплоскость с нормалью $$l$$ в направлении $$l$$ до тех пор, пока дальше уже не будет множества. | ||
| + | И в этот момент считаем скалярное произведение, что равно произведению длины $$l$$ и расстоянию до полученной гиперплоскости. | ||
| + | Если в данном направлении «нет множества», но оно есть в противоположном направлении, то значение функции будет со знаком «минус». | ||
| + | Точка, множество, на котором достигается супремум в определении, называется '''опорным множеством'''. | ||
| + | В случае, когда множество является компактом, супремум можно заменить на максимум, потому что он достигается. | ||
| + | Если же множество к тому же является строго выпуклым, то максимум достигается в единственной точке, которую называют '''опорным вектором'''. | ||
== Свойства == | == Свойства == | ||
== Опорные функции некоторых множеств == | == Опорные функции некоторых множеств == | ||
Версия 17:13, 21 декабря 2020
Одним из удобных инструментов для работы с выпуклыми множествами является математический аппарат опорных функций. Будем рассматривать евклидово пространство $$\mathbb{R}^n$$, хотя опорные функции могут быть определены и для более общего класса линейных пространств.
Определение и интерпретация
Пусть $$Z \subseteq \mathbb{R}^n$$, тогда опорной функцией множества $$Z$$ будем называть функцию $$\rho(\cdot \mid Z) \colon\ \mathbb{R}^n \mapsto \mathbb{R} \cup \{ \pm \infty \}$$, такую что: \[ \begin{cases} \rho (l \mid Z) = \sup \{ \left< l, z \right> \mid z \in Z \}, & Z \neq \varnothing, \\ \rho (l \mid Z) = -\infty, & Z = \varnothing. \end{cases} \]
Опорная функция имеет достаточно простую геометрическую интерпретацию. Рассмотрим множество $$Z$$ на плоскости и некоторое направление $$l$$. Для простоты положим $$\| l \| = 1$$. Тогда опорной функций множества $$Z$$ в направлении $$l$$ будет расстояние (со знаком!) от начала координат до точки множества, наиболее удаленной в данном направлении. То есть мы начинаем отодвигать гиперплоскость с нормалью $$l$$ в направлении $$l$$ до тех пор, пока дальше уже не будет множества. И в этот момент считаем скалярное произведение, что равно произведению длины $$l$$ и расстоянию до полученной гиперплоскости. Если в данном направлении «нет множества», но оно есть в противоположном направлении, то значение функции будет со знаком «минус». Точка, множество, на котором достигается супремум в определении, называется опорным множеством. В случае, когда множество является компактом, супремум можно заменить на максимум, потому что он достигается. Если же множество к тому же является строго выпуклым, то максимум достигается в единственной точке, которую называют опорным вектором.