Опорная функция множества: различия между версиями
Igor (обсуждение | вклад) |
Igor (обсуждение | вклад) |
||
| Строка 41: | Строка 41: | ||
== Опорные функции некоторых множеств == | == Опорные функции некоторых множеств == | ||
| + | |||
| + | === Точка === | ||
| + | Пусть $$z \in \mathbb{R}^n$$. | ||
| + | Супремум в определении вырождается в скалярное произведение и имеем: | ||
| + | \[ | ||
| + | \rho (l \mid z) = \left<l, z\right>. | ||
| + | \] | ||
| + | |||
| + | === Невырожденный эллипсоид === | ||
| + | |||
| + | Пусть $$Z = \mathcal{E}(p, P)$$ — эллипсоид с центром в точке $$p$$ и невырожденной симметричной положительно определенной матрицей конфигурации $$P$$. | ||
| + | По определению эллипсоида $$\mathcal{E}(p, P) = \{ z \in \mathbb{R}^n \mid \left< z - p, P^{-1}(z - p) \right> \leqslant 1 \}$$. | ||
| + | Для начала заметим, что | ||
| + | $$\mathcal{E}(p, P) = p + \mathcal{E}(0, P)$$, откуда $$\rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \rho \bigl(l \mid \mathcal{E}(0, P)\bigr)$$. | ||
| + | Для нахождении опорной функции поставим задачу оптимизации: | ||
| + | \[ | ||
| + | \begin{cases} | ||
| + | \left<l, z\right> \rightarrow \max, \\ | ||
| + | \left<z, P^{-1}z\right> \leqslant 1. | ||
| + | \end{cases} | ||
| + | \] | ||
| + | Так как эллипсоид является выпуклым компактом, то максимум в определении достигается в единственной точке на границе эллипсоида, поэтому задача сводится к более простой: | ||
| + | \[ | ||
| + | \begin{cases} | ||
| + | \left<l, z\right> \rightarrow \max, \\ | ||
| + | \left<z, P^{-1}z\right> = 1. | ||
| + | \end{cases} | ||
| + | \] | ||
| + | Для решения применим метод множителей Лагранжа: | ||
| + | \[ | ||
| + | L(z) = \left<l, z\right> - \frac\lambda2 \left<z, P^{-1}z\right>,\\ | ||
| + | L'(z^*) = 0 = l - \lambda P^{-1}z^*. | ||
| + | \] | ||
| + | Отсюда выражаем $$z^*$$ через $$\lambda$$ и $$l$$ и подставляем в ограничение: | ||
| + | \[ | ||
| + | z^* = \frac1\lambda P l, \\ | ||
| + | \left<z^*, P^{-1}z^*\right> = 1 = \left<\frac1\lambda P l, \frac1\lambda l\right> = \frac1{\lambda^2} \left< Pl, l \right>, \\ | ||
| + | z^* = \frac{Pl}{\sqrt{\left< l, Pl\right>}}. | ||
| + | \] | ||
| + | Получили опорный вектор для направления $$l$$. Подставляя его в скалярное произведение, которое мы максимизируем, получаем: | ||
| + | \[ | ||
| + | \rho\bigl(l \mid \mathcal{E}(0, P)\bigr) = \left<l, z^*\right> = \frac{\left< l, Pl\right>}{\sqrt{\left< l, Pl\right>}} = \sqrt{\left< l, Pl\right>}. | ||
| + | \] | ||
| + | Окончательно для произвольного эллипсоида: | ||
| + | \[ | ||
| + | \rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \sqrt{\left< l, Pl\right>}, \\ | ||
| + | z^* = p + \frac{Pl}{\sqrt{\left< l, Pl\right>}}. | ||
| + | \] | ||
Версия 18:14, 21 декабря 2020
Одним из удобных инструментов для работы с выпуклыми множествами является математический аппарат опорных функций. Будем рассматривать евклидово пространство $$\mathbb{R}^n$$, хотя опорные функции могут быть определены и для более общего класса линейных пространств.
Содержание
Определение и интерпретация
Пусть $$Z \subseteq \mathbb{R}^n$$, тогда опорной функцией множества $$Z$$ будем называть функцию $$\rho(\cdot \mid Z) \colon\ \mathbb{R}^n \mapsto \mathbb{R} \cup \{ \pm \infty \}$$, такую что: \[ \begin{cases} \rho (l \mid Z) = \sup \{ \left< l, z \right> \mid z \in Z \}, & Z \neq \varnothing, \\ \rho (l \mid Z) = -\infty, & Z = \varnothing. \end{cases} \]
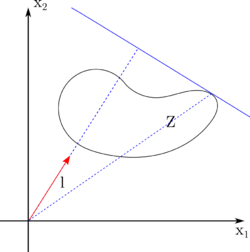
Опорная функция имеет достаточно простую геометрическую интерпретацию. Рассмотрим множество $$Z$$ на плоскости и некоторое направление $$l$$. Для простоты положим $$\| l \| = 1$$. Тогда опорной функций множества $$Z$$ в направлении $$l$$ будет расстояние (со знаком!) от начала координат до точки множества, наиболее удаленной в данном направлении. То есть мы начинаем отодвигать гиперплоскость с нормалью $$l$$ в направлении $$l$$ до тех пор, пока дальше уже не будет множества. И в этот момент считаем скалярное произведение, что равно произведению длины $$l$$ и расстоянию до полученной гиперплоскости. Если в данном направлении «нет множества», но оно есть в противоположном направлении, то значение функции будет со знаком «минус». Множество, на котором достигается супремум в определении, называется опорным множеством. В случае, когда множество является компактом, супремум можно заменить на максимум, потому что он достигается. Если же множество к тому же является строго выпуклым, то максимум достигается в единственной точке, которую называют опорным вектором.
Свойства
Свойства опорной функции как функции от $$l$$:
- Выпуклость: $$\rho\bigl(\alpha l_1 + (1 - \alpha)l_2 \mid Z\bigr) \leqslant \alpha \rho(l_1 \mid Z) + (1 - \alpha) \rho(l_2 \mid Z), \quad \forall \alpha \in [0, 1]$$, \quad \forall l_1, l_2 \in \mathbb{R}^n.
- Положительная однородность: $$\rho(\alpha l \mid Z) = \alpha \rho(l \mid Z), \quad \forall \alpha > 0, \quad \forall l \in \mathbb{R}^n$$.
- Если $$Z$$ — ограниченное множество, то опорная функция принимает только конечные значения из $$\mathbb{R}$$.
- Ключевое свойство, делающее аппарат опорных функций крайне удобным: для любой выпуклой положительно однородной функции, принимающей конечные значения, существует единственный выпуклый компакт, для которого эта функция является опорной.
Свойства как функции от $$Z$$:
- Неотрицательная однородность: $$\rho (l \mid \alpha Z) = \alpha \rho (l \mid Z), \quad \forall Z \neq \varnothing$$.
- Аддитивность $$\rho(l \mid Z_1 + Z_2) = \rho(l \mid Z_1) + \rho(l \mid Z_2), \quad \forall Z_1, Z_2 \neq \varnothing$$, где сумма понимается в смысле Минковского.
- Опорная функция любого замкнутого множества равно опорной функции его выпуклой оболочки.
- Опорная функция объединения множеств равна максимуму из опорных функций множеств: $$\rho(l \mid Z_1 \cup Z_2) = \rho(l \mid Z_1) \vee \rho(l \mid Z_2), \quad \forall Z_1, Z_2 \neq \varnothing$$
- Опорная функция пересечения множеств равна наибольшей выпуклой функции, не превосходящей минимум из опорных функций множеств: $$\rho(l \mid Z_1 \cap Z_2) = \mathrm{conv} \bigl( \rho(l \mid Z_1) \wedge \rho(l \mid Z_2)\bigr), \quad \forall Z_1, Z_2 \neq \varnothing$$
Опорные функции некоторых множеств
Точка
Пусть $$z \in \mathbb{R}^n$$. Супремум в определении вырождается в скалярное произведение и имеем: \[ \rho (l \mid z) = \left<l, z\right>. \]
Невырожденный эллипсоид
Пусть $$Z = \mathcal{E}(p, P)$$ — эллипсоид с центром в точке $$p$$ и невырожденной симметричной положительно определенной матрицей конфигурации $$P$$. По определению эллипсоида $$\mathcal{E}(p, P) = \{ z \in \mathbb{R}^n \mid \left< z - p, P^{-1}(z - p) \right> \leqslant 1 \}$$. Для начала заметим, что $$\mathcal{E}(p, P) = p + \mathcal{E}(0, P)$$, откуда $$\rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \rho \bigl(l \mid \mathcal{E}(0, P)\bigr)$$. Для нахождении опорной функции поставим задачу оптимизации: \[ \begin{cases} \left<l, z\right> \rightarrow \max, \\ \left<z, P^{-1}z\right> \leqslant 1. \end{cases} \] Так как эллипсоид является выпуклым компактом, то максимум в определении достигается в единственной точке на границе эллипсоида, поэтому задача сводится к более простой: \[ \begin{cases} \left<l, z\right> \rightarrow \max, \\ \left<z, P^{-1}z\right> = 1. \end{cases} \] Для решения применим метод множителей Лагранжа: \[ L(z) = \left<l, z\right> - \frac\lambda2 \left<z, P^{-1}z\right>,\\ L'(z^*) = 0 = l - \lambda P^{-1}z^*. \] Отсюда выражаем $$z^*$$ через $$\lambda$$ и $$l$$ и подставляем в ограничение: \[ z^* = \frac1\lambda P l, \\ \left<z^*, P^{-1}z^*\right> = 1 = \left<\frac1\lambda P l, \frac1\lambda l\right> = \frac1{\lambda^2} \left< Pl, l \right>, \\ z^* = \frac{Pl}{\sqrt{\left< l, Pl\right>}}. \] Получили опорный вектор для направления $$l$$. Подставляя его в скалярное произведение, которое мы максимизируем, получаем: \[ \rho\bigl(l \mid \mathcal{E}(0, P)\bigr) = \left<l, z^*\right> = \frac{\left< l, Pl\right>}{\sqrt{\left< l, Pl\right>}} = \sqrt{\left< l, Pl\right>}. \] Окончательно для произвольного эллипсоида: \[ \rho\bigl(l \mid \mathcal{E}(p, P)\bigr) = \left<l, p\right> + \sqrt{\left< l, Pl\right>}, \\ z^* = p + \frac{Pl}{\sqrt{\left< l, Pl\right>}}. \]