Отделимость множеств: различия между версиями
Oleg23 (обсуждение | вклад) |
Oleg23 (обсуждение | вклад) |
||
| Строка 7: | Строка 7: | ||
== Определения == | == Определения == | ||
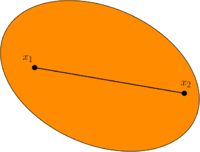
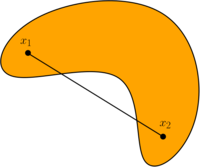
| − | '''Определение 1.''' ''Аффинной комбинацией'' точек $$x_1, x_2, \ldots, x_n \in X$$ назовём выражение $$\sum_{i = 1} ^ n \alpha_i x_i$$, где числа $$\forall i \, \alpha_i \geqslant 0, \, \sum_{i = 1} ^ n \alpha_i = 1$$. | + | '''Определение 1.''' ''Аффинной комбинацией'' точек $$x_1, x_2, \ldots, x_n \in X$$ назовём выражение $$\sum_{i = 1} ^ n \alpha_i x_i$$, где числа $$\alpha_1, \alpha_2, \ldots, \alpha_n$$ удовлетворяют условиям $$\forall i \, \alpha_i \geqslant 0, \, \sum_{i = 1} ^ n \alpha_i = 1$$. |
| − | '''Определение 2.''' | + | '''Определение 2.''' ''Аффинной оболочкой'' множества $$A$$ назовём множество всевозможных аффинных комбинаций точек множества $$A: aff A := |
| + | \{\sum_{i = 1} ^ n \alpha_i x_i | n \in \mathbb N, \, \forall i \, \alpha_i \geqslant 0, \, x_1, \, x_2, \ldots, x_n \in X \}$$. | ||
| − | '''Определение 3.''' | + | '''Определение 3.''' ''Относительной внутренностью'' множества $$A$$ назовём его "внутренность относительно аффинной оболочки $$A$$", то есть множество точек $$ri A := \{x \in X | \exists \varepsilon > 0: O(x, \, \varepsilon) \cap aff A \subset A\}$$. |
'''Определение 4.''' | '''Определение 4.''' | ||
Версия 23:39, 25 октября 2023
Для получения многих результатов в выпуклом анализе ключевую роль занимают теоремы об отделимости выпуклых множеств. Дадим необходимые определения.
Далее будем считать, что $$X$$ - нормированное пространство, а $$A$$ и $$B$$ - его непустые подмножества. Дадим необходимые определения.
Определения
Определение 1. Аффинной комбинацией точек $$x_1, x_2, \ldots, x_n \in X$$ назовём выражение $$\sum_{i = 1} ^ n \alpha_i x_i$$, где числа $$\alpha_1, \alpha_2, \ldots, \alpha_n$$ удовлетворяют условиям $$\forall i \, \alpha_i \geqslant 0, \, \sum_{i = 1} ^ n \alpha_i = 1$$.
Определение 2. Аффинной оболочкой множества $$A$$ назовём множество всевозможных аффинных комбинаций точек множества $$A: aff A := \{\sum_{i = 1} ^ n \alpha_i x_i | n \in \mathbb N, \, \forall i \, \alpha_i \geqslant 0, \, x_1, \, x_2, \ldots, x_n \in X \}$$.
Определение 3. Относительной внутренностью множества $$A$$ назовём его "внутренность относительно аффинной оболочки $$A$$", то есть множество точек $$ri A := \{x \in X | \exists \varepsilon > 0: O(x, \, \varepsilon) \cap aff A \subset A\}$$.
Определение 4.
Определение 5.
1. Множества $$A$$ и $$B$$ отделимы, если найдётся такой линейный непрерывный функционал $$l\not=0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right>\leq\inf\limits_{x \in A}\left<l, y\right>. \end{gather*}
2. Множества $$A$$ и $$B$$ строго отделимы, если найдётся такой линейный непрерывный функционал $$l\not=0$$, что \begin{gather*} \sup\limits_{x \in A}\left<l, x\right><\inf\limits_{x \in A}\left<l, y\right>. \end{gather*} Также говорят, что функционал $$l$$ разделяет (строго разделяет) множества $$A$$ и $$B$$
Теоремы отделимости
Заметим, что множества $$A$$ и $$B$$ можно отделимы тогда и только тогда, когда множество $$(A − B)$$ можно отделить от $$\{0\}$$ (множества, состоящего из одного нуля). Этим фактом мы воспользуемся при доказательстве следующей теоремы.
Теорема (о конечномерной отделимости)
Формулировка теоремы:
Пусть $$A, B$$ — непустые выпуклые подмножества $$R^n$$ и их относительные внутренности $$ri A$$ и $$ri B$$ не пересекаются. Тогда множества A и B можно отделить.
Доказательство:
Заметим, что так как $$ri A$$ и $$ri B$$ не пересекаются, то $$0\not\in (ri A-ri B)$$. Множество $$(ri A-ri B)$$ выпукло $$\Longrightarrow$$ (указать ссылку на лемму 1.4.2) $$\Longrightarrow$$ $$(ri A-ri B)$$ отделимо от нуля, а значит $$ri A$$ и $$ri B$$ отделимы, т.е. $$\exists l\not=0$$ и $$\gamma\in\mathbb{R}:$$$$\forall x\in{ri A},y\in{ri B} \Longrightarrow\left<l, x\right>\leq\gamma\leq\left<l, y\right>$$.
Пусть $$x \in A$$. Тогда существует последовательность точек $$\{x_i\}$$, лежащая в $$ri A$$ и сходящаяся к $$x$$. Поэтому, $$\left<l, x_i\right>\leq\gamma,$$ $$\forall i$$. Переходя к пределу по $$i$$, получаем, что, $$\left<l, x\right>\leq\gamma$$. Поступив аналогично для точек $$y$$ множества $$B$$, получим, что полученный линейный непрерывный функционал $$l$$ также разделяет $$A$$ и $$B$$.$$~~\blacksquare$$