Неподвижные точки системы: различия между версиями
Kirich23 (обсуждение | вклад) |
Kirich23 (обсуждение | вклад) |
||
| Строка 115: | Строка 115: | ||
\] | \] | ||
| − | Согласно теореме 1 точка $$v^{*}=r^{1/b}-1$$ будет асимптотически устойчивой, при $$r^{-1/b}<1$$ | + | Согласно теореме 1 точка $$v^{*}=r^{1/b}-1$$ будет |
| + | |||
| + | асимптотически устойчивой, при $$r^{-1/b}<1$$ | ||
| + | неустойчивой, при $$r^{-1/b}>1$$. | ||
| + | |||
Отметим, что точка $$v^{*}=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, | Отметим, что точка $$v^{*}=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, | ||
таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, | таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, | ||
| Строка 126: | Строка 130: | ||
f_v(v^{*})=r. | f_v(v^{*})=r. | ||
\] | \] | ||
| − | Таким образом, по теореме 1, точка $$v^{*}=0$$ будет асимптотически устойчивой, при $$r<1$$ | + | Таким образом, по теореме 1, точка $$v^{*}=0$$ будет |
| + | асимптотически устойчивой, при $$r<1$$ | ||
| + | неустойчивой, при $$r>1$$. | ||
== Связанные теоремы == | == Связанные теоремы == | ||
Версия 19:26, 19 декабря 2023
Пусть задана динамическая система:
\begin{equation} \label{sist1} \frac{du}{dt} = f(u),\ u \in U \subseteq \mathbb{R}^n,\ f : U → \mathbb{R}^n, \end{equation}
Определение 1.
Неподвижными точками динамической системы (\ref{sist1}) называются такие точки пространства состояний $$u^{∗}$$, что $$f(u^{∗}) = u^{∗}$$.
Кроме термина "неподвижная точка" используют иногда термины "стационарная точка" или "положение равновесия".
Содержание
Устойчивость неподвижных точек
Реальная система подвержена внешним воздействиям, она не может находиться все время в одном и том же состоянии. Если немного возмутить состояние системы так, что ее состояние окажется в некоторой окрестности положения равновесия, то возможны следующие сценарии: траектории могут покинуть эту окрестность, остаться в этой окрестности, или приблизиться к положению равновесия. Естественно назвать положение равновесия неустойчивым в первом случае и устойчивым в двух других.
Определение 2.
Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется устойчивой по Ляпунову, если для любого $$\varepsilon > 0$$ существует такое $$\delta > 0$$, что для любых начальных данных $$u(t_0)$$ из $$\delta$$-окрестности точки $$u^{*}$$ вся траектория системы $$u(t)$$ содержится в $$\varepsilon$$-окрестности точки $$u^{*}$$.
$$\forall \varepsilon > 0 ~ \exists \delta(\varepsilon) ~ \forall u(t_0) \in \mathcal{U}_{\delta}(u^{*})$$, $$|u^{*}-u(t)|< \varepsilon, ~\forall t \geqslant t_0$$.
Определение 3.
Неподвижная точка $$u^{*}$$ отображения (\ref{sist1}) называется асимптотически устойчивой, если она является устойчивой по Ляпунову и кроме того $$\displaystyle{\lim_{t\to\infty}} u(t) = u^{*}$$.
Если положение равновесия не является устойчивым, то говорят, что оно неустойчиво. Асимптотически устойчивые неподвижные точки иногда называют аттракторами, а неустойчивые неподвижные точки иногда называют репеллерами.
Теорема 1.
Пусть $$u^{*}$$ — неподвижная точка отображения (\ref{sist1}), т.е. $$u^{*}$$ = $$f(u^{*})$$, и пусть $$f$$ обратима в малой окрестности $$u^{*}$$. Тогда $$u^{*}$$ асимптотически устойчива, если $$|f^{'}(u^{*})| < 1$$, и неустойчива, если $$|f^{'}(u^{*})| > 1$$. Если $$ |f^{'}(u^{*})| = 1$$, то требуются дополнительные исследования.
Доказательство.
Пусть $$|f^{'}(u^{*})| < 1$$ и пусть $$u$$ принадлежит малой окрестности $$u^{*}$$. Так как \[ \displaystyle{\lim_{t\to\infty}} \frac{|f(u)-f(u^{*})|}{|u-u^{*}|}=|f^{'}(u^{*})|, \] поэтому существует такая окрестность $$u^{*}$$, что \[ \frac{|f(u)-f(u^{*})|}{|u-u^{*}|} \leqslant a, \] для всех $$u$$ из этой окрестности; здесь $$a$$ — некоторое число, такое что $$|f^{'}(u^{*})| \leqslant a < 1$$. Таким образом, $$f(u)$$ остается в той же окрестности, что и $$u$$, и, кроме того, ближе к неподвижной точке $$u^{*}$$, по крайней мере, на множитель $$a$$. Отсюда следует, что \[|f(f(u)) − f(f(u^{*}))| \leqslant a |f(u) − f(u^{*})| \leqslant a^2|u − u^{*}|, \] или, по индукции, \[|f^{k}(u) − u^{*}| \leqslant a^{k}|u − u^{*}|, \] где $$f^{k}$$ обозначает $$k$$-ую суперпозицию отображения $$f$$. Таким образом мы доказали, что последовательность $$f^{k}(u)$$ будет сходиться к $$u^{*}$$, то есть является асимптотически устойчивой.
Вторая часть утверждения доказывается сходным образом. $$\blacksquare$$
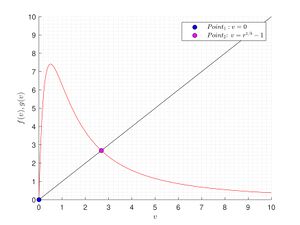
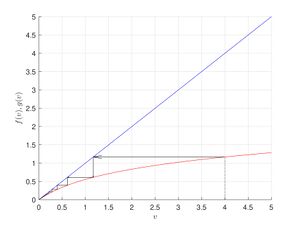
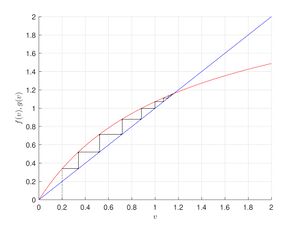
Пример поиска неподвижных точек с помощью графического метода
Пусть задана система $$v_{t+1} = \frac{r v_t}{(1+ v_t)^b}$$.
Графически неподвижные точки — это точки пересечения графика функции $$f(v)$$ и биссектрисы первого координатного угла $$v_{t+1} = v_{t}$$ (нас интересуют только неотрицательные решения). Для нахождения неподвижных точек заданной системы рассмотрим возможные пересечения графика функции $$f(v)=\frac{rv}{(1+v)^b}$$ с прямой $$g(v)=v$$.
Заметим, что система \begin{equation} \label{sist2} \begin{cases} f(v)=\frac{rv}{(1+v)^b},\\g(v)=v. \end{cases} \end{equation} при любых $$v \geqslant 0, ~r,b > 0$$ имеет хотя бы один корень, а именно $$v=0$$. Второй корень $$v=r^{1/b}-1$$ система может иметь только при значении параметра $$r> 1$$. Больше двух неотрицательных корней система (\ref{sist2}) не имеет.
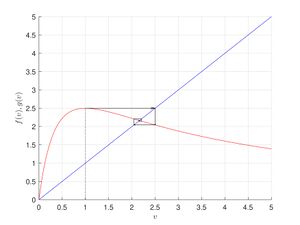
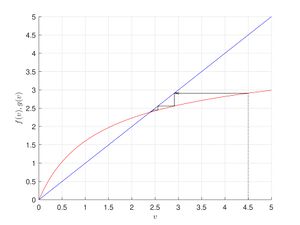
Пример исследования неподвижных точек на устойчивость
Исследуем на устойчивость неподвижные точки $$v^{*}=r^{1/b}-1$$ и $$v^{*}=0$$ для системы (\ref{sist2}).
\[ f_v(v^{*})=\frac{r((1+v)^b-bv(1+v)^{b-1})}{(1+v)^{2b}}. \]
1. Исследование первой точки $$v^{*}=r^{1/b}-1$$:
Подставим $$v^{*}=r^{1/b}-1$$ в выражение (\ref{sist2}) и с учетом наложенных ограничений $$r>1, b>0$$ для существования точки получим
\[ f_v(v^{*})=b(r^{-1/b}-1)+1. \]
Согласно теореме 1 точка $$v^{*}=r^{1/b}-1$$ будет
асимптотически устойчивой, при $$r^{-1/b}<1$$ неустойчивой, при $$r^{-1/b}>1$$.
Отметим, что точка $$v^{*}=r^{1/b}-1$$ (отличная от нуля) существует только при значении параметра $$r > 1$$, таким образом $$r^{-1/b}$$ принимает значения меньше единицы при любых $$r> 1$$, значит, точка $$v^{*}=r^{1/b}-1$$ асимптотически устойчива всегда, если она существует.
2. Исследование второй точки $$v^{*}=0$$:
Подставим $$v^{*}=0$$ в выражение (\ref{sist2}) и получим \[ f_v(v^{*})=r. \] Таким образом, по теореме 1, точка $$v^{*}=0$$ будет асимптотически устойчивой, при $$r<1$$ неустойчивой, при $$r>1$$.
Связанные теоремы
Теорема 2. (Банах)
Пусть $$(X, d)$$ — полное метрическое пространство с метрикой $$d$$.
Пусть задано отображение $$f : X \rightarrow X$$ и существует число $$a, 0 \leqslant a < 1$$, такое, что для любых $$x, y \in X: d(f(x), f(y)) \leqslant a \cdot d(x, y)$$.
Тогда существует единственная точка $$\xi \in X$$ такая, что $$f(\xi) = \xi$$, и начиная с любой точки $$x_0 \in X$$, последовательность итераций $${f_n(x_0)}_{n=1,2,...}$$ сходится к точке $$\xi$$.
Теорема 3. (Брауэр)
Любое непрерывное отображение замкнутого шара в себя в конечномерном евклидовом пространстве имеет неподвижную точку.
Более подробно, рассмотрим замкнутый шар в $$n$$-мерном пространстве \(B^n\subset \mathbb R^n\). Пусть \(f \colon B^n\to B^n\) — некоторое непрерывное отображение этого шара в себя (не обязательно строго внутрь себя, не обязательно биективное, т.е. даже не обязательно сюръективное). Тогда найдется такая точка \(x\in B^n\), что \(f(x)=x\).
Теорема 4. (Шаудер — Тихонов)
В локально выпуклом топологическом векторном пространстве любое непрерывное отображение $$f : K\to K$$ выпуклого компактного множества $$K$$ в себя имеет неподвижную точку.
Список литературы
1. Братусь А.С., Новожилов А.С., Платонов А.П. Динамические системы и модели биологии, 2011.
2. Абрамова В.В. Лекции по курсу "Динамические системы и биоматематика", 2023.
3. Banach S. Sur les opérations dans les ensembles abstraits et leur applications aux équations integrales, Fund. Math, 1922
4. Шашкин Ю.А. Неподвижные точки, М.: Наука, 1989
5. J. Schauder, Der Fixpunktsatz in Funktionalräumen, Studia Math. 2, 1930