Выпуклое множество и его свойства: различия между версиями
| Строка 1: | Строка 1: | ||
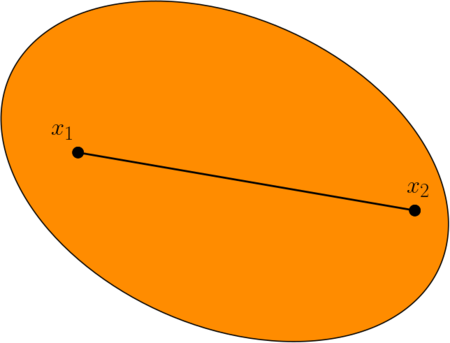
| + | [[Файл:New_ellips.png|450px|thumb|frame|right|Пример выпуклого множества.]] | ||
'''Выпуклое множество''' в линейном пространстве — множество, содержащее любые две его точки вместе с отрезком, соединяющим их. Выпуклые множества играют важную роль во многих оптимизационных задачах. | '''Выпуклое множество''' в линейном пространстве — множество, содержащее любые две его точки вместе с отрезком, соединяющим их. Выпуклые множества играют важную роль во многих оптимизационных задачах. | ||
| Строка 19: | Строка 20: | ||
* Пересечение любого числа выпуклых множеств $$A_\sigma\subset X,~\sigma\in\Sigma$$ является выпуклым множеством. | * Пересечение любого числа выпуклых множеств $$A_\sigma\subset X,~\sigma\in\Sigma$$ является выпуклым множеством. | ||
| − | Возьмем произвольные точки $$x, y \in \bigcap_{\sigma \in \Sigma} A_\sigma$$. Каждое из множеств $$A_\sigma$$ является выпуклым. Поэтому $$[x, y] \subset A_\sigma$$ для любого $$\sigma \in \Sigma$$. Отсюда $$[x, y] \subset \bigcap_{a \in \Sigma} A_\sigma$$, что по определению означает выпуклость пересечения множеств $$\bigcap_{\sigma \in \Sigma} A_\sigma$$. | + | Доказательство: |
| + | |||
| + | Возьмем произвольные точки $$x, y \in \bigcap_{\sigma \in \Sigma} A_\sigma$$. Каждое из множеств $$A_\sigma$$ является выпуклым. Поэтому $$[x, y] \subset A_\sigma$$ для любого $$\sigma \in \Sigma$$. Отсюда $$[x, y] \subset \bigcap_{a \in \Sigma} A_\sigma$$, что по определению означает выпуклость пересечения множеств $$\bigcap_{\sigma \in \Sigma} A_\sigma$$. $$~~\blacksquare$$ | ||
* Пусть $$A_1,\ldots,A_n$$ — выпуклые подмножества $$X,~\alpha_1,\ldots,\alpha_n\in\mathbb{R}$$. Тогда множество $$\sum_{k=1}^n\alpha_i A_i$$ выпукло. | * Пусть $$A_1,\ldots,A_n$$ — выпуклые подмножества $$X,~\alpha_1,\ldots,\alpha_n\in\mathbb{R}$$. Тогда множество $$\sum_{k=1}^n\alpha_i A_i$$ выпукло. | ||
| + | |||
| + | Доказательство: | ||
Возьмем произвольные точки $$x, y \in \sum_{i=1}^n \alpha_i A_i$$. По определению существуют $$x_1, y_1 \in A_1, \ldots, x_n, y_n \in A_n$$ такие, что | Возьмем произвольные точки $$x, y \in \sum_{i=1}^n \alpha_i A_i$$. По определению существуют $$x_1, y_1 \in A_1, \ldots, x_n, y_n \in A_n$$ такие, что | ||
| Строка 33: | Строка 38: | ||
(\alpha+\beta) A \subset \alpha A+\beta A | (\alpha+\beta) A \subset \alpha A+\beta A | ||
\end{gather*} | \end{gather*} | ||
| − | справедливое для произвольного множества $$А$$ и чисел $$\alpha, \beta$$. | + | справедливое для произвольного множества $$А$$ и чисел $$\alpha, \beta$$. $$~~\blacksquare$$ |
* Пусть $$A$$ — выпуклое множество. Тогда для любых $$\alpha\geq0,~\beta\geq0$$ справедлива формула | * Пусть $$A$$ — выпуклое множество. Тогда для любых $$\alpha\geq0,~\beta\geq0$$ справедлива формула | ||
| Строка 39: | Строка 44: | ||
(\alpha+\beta)A=\alpha A+\beta A. | (\alpha+\beta)A=\alpha A+\beta A. | ||
\end{gather*} | \end{gather*} | ||
| + | |||
| + | Доказательство: | ||
В силу сказанного выше достаточно доказать включение $$\alpha A+\beta A\subset(\alpha+\beta)A.$$ Если $$\alpha+\beta=0$$, то $$\alpha=\beta=0$$ и, значит, это включение очевидно. Рассмотрим случай $$\alpha+\beta>0$$. Пусть $$\xi\in\alpha A+\beta A$$. Тогда $$\xi=\alpha x_1+\beta x_2$$ для некоторых $$x_1,x_2\in A$$, откуда в силу выпуклости $$A$$ имеем | В силу сказанного выше достаточно доказать включение $$\alpha A+\beta A\subset(\alpha+\beta)A.$$ Если $$\alpha+\beta=0$$, то $$\alpha=\beta=0$$ и, значит, это включение очевидно. Рассмотрим случай $$\alpha+\beta>0$$. Пусть $$\xi\in\alpha A+\beta A$$. Тогда $$\xi=\alpha x_1+\beta x_2$$ для некоторых $$x_1,x_2\in A$$, откуда в силу выпуклости $$A$$ имеем | ||
| Строка 44: | Строка 51: | ||
\xi=(\alpha+\beta)\left(\dfrac{\alpha}{\alpha+\beta}x_1+\dfrac{\beta}{\alpha+\beta}x_2\right)\in(\alpha+\beta)A, | \xi=(\alpha+\beta)\left(\dfrac{\alpha}{\alpha+\beta}x_1+\dfrac{\beta}{\alpha+\beta}x_2\right)\in(\alpha+\beta)A, | ||
\end{gather*} | \end{gather*} | ||
| − | что завершает доказательство нужного включения. | + | что завершает доказательство нужного включения. $$~~\blacksquare$$ |
* Выпуклое множество $$A$$ содержит любую выпуклую комбинацию своих точек. | * Выпуклое множество $$A$$ содержит любую выпуклую комбинацию своих точек. | ||
| + | |||
| + | Доказательство: | ||
Необходимо показать, что для любого $$n\geq2$$ из того, что | Необходимо показать, что для любого $$n\geq2$$ из того, что | ||
| Строка 60: | Строка 69: | ||
\sum_{i=1}^{r+1}\alpha_i x_i=\sum_{i=1}^r\alpha_i\left(\sum_{i=1}^r\dfrac{\alpha_i}{\sum_{i=1}^r\alpha_i}x_i\right)+\alpha_{r+1}x_{r+1}=\tilde{\alpha}\tilde{x}+\alpha_{r+1}x_{r+1}\in A | \sum_{i=1}^{r+1}\alpha_i x_i=\sum_{i=1}^r\alpha_i\left(\sum_{i=1}^r\dfrac{\alpha_i}{\sum_{i=1}^r\alpha_i}x_i\right)+\alpha_{r+1}x_{r+1}=\tilde{\alpha}\tilde{x}+\alpha_{r+1}x_{r+1}\in A | ||
\end{gather*} | \end{gather*} | ||
| − | в силу выпуклости множества $$A$$. Здесь $$\tilde{x}\in A$$ в силу выпуклости $$A$$ и предположения индукции, а $$\tilde{\alpha}=\sum_{i=1}^r\alpha_i$$, следовательно, $$\tilde{\alpha}+\alpha_{r+1}=1$$. | + | в силу выпуклости множества $$A$$. Здесь $$\tilde{x}\in A$$ в силу выпуклости $$A$$ и предположения индукции, а $$\tilde{\alpha}=\sum_{i=1}^r\alpha_i$$, следовательно, $$\tilde{\alpha}+\alpha_{r+1}=1$$. $$~~\blacksquare$$ |
<br> | <br> | ||
Версия 22:08, 1 ноября 2022
Выпуклое множество в линейном пространстве — множество, содержащее любые две его точки вместе с отрезком, соединяющим их. Выпуклые множества играют важную роль во многих оптимизационных задачах.
Определения выпуклого множества и выпуклой комбинации точек
1. Множество $$A$$ называется выпуклым, если для любых двух точек $$x_1,x_2\in A$$ выполняется \begin{gather*} [x_1,x_2]\subset A, \text{ т.е. } \alpha x_1+(1-\alpha x_2)\in A~~\forall\alpha\in[0,1]. \end{gather*}
2. Сумма $$\sum_{i=1}^k\alpha_i x_i$$ называется выпуклой комбинацией точек $$x_1,\ldots,x_k$$, если $$\alpha_i\geq0,~i=1,\ldots,k,~\sum_{i=1}^k\alpha_i=1$$.
3. Пусть $$A,B\subset X$$ и $$\alpha\in\mathbb{R}$$. Введем в рассмотрение множества \begin{gather*} A+B=\{x\in X: ~x=a+b,~a\in A,~b\in B\},\\ \alpha A=\{x\in X: x=\alpha a, ~a\in A\}. \end{gather*}
Свойства выпуклых множеств
- Пересечение любого числа выпуклых множеств $$A_\sigma\subset X,~\sigma\in\Sigma$$ является выпуклым множеством.
Доказательство:
Возьмем произвольные точки $$x, y \in \bigcap_{\sigma \in \Sigma} A_\sigma$$. Каждое из множеств $$A_\sigma$$ является выпуклым. Поэтому $$[x, y] \subset A_\sigma$$ для любого $$\sigma \in \Sigma$$. Отсюда $$[x, y] \subset \bigcap_{a \in \Sigma} A_\sigma$$, что по определению означает выпуклость пересечения множеств $$\bigcap_{\sigma \in \Sigma} A_\sigma$$. $$~~\blacksquare$$
- Пусть $$A_1,\ldots,A_n$$ — выпуклые подмножества $$X,~\alpha_1,\ldots,\alpha_n\in\mathbb{R}$$. Тогда множество $$\sum_{k=1}^n\alpha_i A_i$$ выпукло.
Доказательство:
Возьмем произвольные точки $$x, y \in \sum_{i=1}^n \alpha_i A_i$$. По определению существуют $$x_1, y_1 \in A_1, \ldots, x_n, y_n \in A_n$$ такие, что \begin{gather*} x=\sum_{i=1}^n \alpha_i x_i, \quad y=\sum_{i=1}^n \alpha_i y_i. \end{gather*} Из выпуклости множеств $$A_i$$ следует, что для любых $$\alpha, \beta \geq 0$$, $$\alpha+\beta=1$$, имеет место $$\alpha x_i+\beta y_i \in A_i$$ и, значит, $$\alpha x+\beta y=$$ $$=\sum_{i=1}^n \alpha_i\left(\alpha x_i+\beta y_i\right) \in \sum_{i=1}^n \alpha_i A_i$$, откуда вытекает выпуклость множества $$\sum_{i=1}^n \alpha_i A_i$$
Из определения операции суммы множеств и произведения множества на число непосредственно вытекает включение \begin{gather*} (\alpha+\beta) A \subset \alpha A+\beta A \end{gather*} справедливое для произвольного множества $$А$$ и чисел $$\alpha, \beta$$. $$~~\blacksquare$$
- Пусть $$A$$ — выпуклое множество. Тогда для любых $$\alpha\geq0,~\beta\geq0$$ справедлива формула
\begin{gather*} (\alpha+\beta)A=\alpha A+\beta A. \end{gather*}
Доказательство:
В силу сказанного выше достаточно доказать включение $$\alpha A+\beta A\subset(\alpha+\beta)A.$$ Если $$\alpha+\beta=0$$, то $$\alpha=\beta=0$$ и, значит, это включение очевидно. Рассмотрим случай $$\alpha+\beta>0$$. Пусть $$\xi\in\alpha A+\beta A$$. Тогда $$\xi=\alpha x_1+\beta x_2$$ для некоторых $$x_1,x_2\in A$$, откуда в силу выпуклости $$A$$ имеем \begin{gather*} \xi=(\alpha+\beta)\left(\dfrac{\alpha}{\alpha+\beta}x_1+\dfrac{\beta}{\alpha+\beta}x_2\right)\in(\alpha+\beta)A, \end{gather*} что завершает доказательство нужного включения. $$~~\blacksquare$$
- Выпуклое множество $$A$$ содержит любую выпуклую комбинацию своих точек.
Доказательство:
Необходимо показать, что для любого $$n\geq2$$ из того, что \begin{gather*} x=\sum_{i=1}^n\alpha_i x_i,\quad x_i\in A,~\alpha_i\geq0,\quad\sum_{i=1}^n\alpha_i=1, \end{gather*} следует, что $$x\in A$$.
Докажем по индукции. При $$n=2$$ искомое утверждение следует из определения выпуклого множества. Пусть искомое утверждение доказано для $$n=r$$. Докажем его для $$n=r+1$$.
Не ограничивая общности рассуждений, будем считать, что $$\sum_{i=1}^r\alpha_i>0.$$ Тогда \begin{gather*} \sum_{i=1}^{r+1}\alpha_i x_i=\sum_{i=1}^r\alpha_i\left(\sum_{i=1}^r\dfrac{\alpha_i}{\sum_{i=1}^r\alpha_i}x_i\right)+\alpha_{r+1}x_{r+1}=\tilde{\alpha}\tilde{x}+\alpha_{r+1}x_{r+1}\in A \end{gather*} в силу выпуклости множества $$A$$. Здесь $$\tilde{x}\in A$$ в силу выпуклости $$A$$ и предположения индукции, а $$\tilde{\alpha}=\sum_{i=1}^r\alpha_i$$, следовательно, $$\tilde{\alpha}+\alpha_{r+1}=1$$. $$~~\blacksquare$$
Список литературы
1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004.