Задача быстродействия "из множества во множество": различия между версиями
Gleb22 (обсуждение | вклад) |
Gleb22 (обсуждение | вклад) |
||
| Строка 5: | Строка 5: | ||
\dot x(t) = A(t)x(t) + B(t)u(t) + f(t), \\ | \dot x(t) = A(t)x(t) + B(t)u(t) + f(t), \\ | ||
x(t_0) \in \mathcal{X}^0, x(t_1) \in \mathcal{X}^1, \\ | x(t_0) \in \mathcal{X}^0, x(t_1) \in \mathcal{X}^1, \\ | ||
| − | u(t) \in \mathcal{P}(t) \in \text{conv}\mathbb{R}^ | + | u(t) \in \mathcal{P}(t) \in \text{conv}\mathbb{R}^m, \\ |
\mathcal{X}^0, \mathcal{X}^1 \in \text{conv}\mathbb{R}^n, \\ | \mathcal{X}^0, \mathcal{X}^1 \in \text{conv}\mathbb{R}^n, \\ | ||
t_0 ~- \text{фиксировано}, \\ | t_0 ~- \text{фиксировано}, \\ | ||
| Строка 12: | Строка 12: | ||
где \( A(t), B(t), f(t) ~-\) непрерывны, а \( \mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \( l: \rho(l\vert\mathcal{P}(\tau))\) по \(\tau\) непрерывна\(^1\)). | где \( A(t), B(t), f(t) ~-\) непрерывны, а \( \mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \( l: \rho(l\vert\mathcal{P}(\tau))\) по \(\tau\) непрерывна\(^1\)). | ||
| − | \(^1\)В частности, при \( | + | \(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P}(\tau) = [a(\tau), b(\tau)]\); неперерывность многозначного отображения означает, что \(a(\tau), b(\tau)~-\) непрерывны. |
== Множества достижимости и разрешимости == | == Множества достижимости и разрешимости == | ||
Текущая версия на 14:09, 25 ноября 2022
Содержание
Постановка задачи
Задача быстродействия\(~-\) задача перевода системы из начального фиксированного положения в конечное, также фиксированное, положение за минимальное время. Пусть система определяется условиями: \begin{cases} \dot x(t) = A(t)x(t) + B(t)u(t) + f(t), \\ x(t_0) \in \mathcal{X}^0, x(t_1) \in \mathcal{X}^1, \\ u(t) \in \mathcal{P}(t) \in \text{conv}\mathbb{R}^m, \\ \mathcal{X}^0, \mathcal{X}^1 \in \text{conv}\mathbb{R}^n, \\ t_0 ~- \text{фиксировано}, \\ t_1 - t_0 \rightarrow \underset{u(\cdot)}{\text{inf}}, \end{cases} где \( A(t), B(t), f(t) ~-\) непрерывны, а \( \mathcal{P} \) непрерывно как многозначное отображение (это требование гарантирует нам, что для любого \( l: \rho(l\vert\mathcal{P}(\tau))\) по \(\tau\) непрерывна\(^1\)).
\(^1\)В частности, при \(m=1\) множество \(\mathcal{P}\) выглядит как \(\mathcal{P}(\tau) = [a(\tau), b(\tau)]\); неперерывность многозначного отображения означает, что \(a(\tau), b(\tau)~-\) непрерывны.
Множества достижимости и разрешимости
Множеством достижимости в момент времени \(t\) будем называть: \[ \mathcal{X}[t] = \mathcal{X}(t, t_0, \mathcal{X}^0) = \{x| \exists u(\cdot) - \text{измеримая, т.ч.} \forall \tau \leqslant t: u(\tau) \in \mathcal{P}(\tau), \exists x^0 \in \mathcal{X}^0: x(t, t_0, x^0| u(\cdot)) = x\} = \underset{x^0 \in \mathcal{X}^0}{\cup}\mathcal{X}(t, t_0, x^0). \]
Множеством разрешимости в момент времени \(t\) будем называть: \[ \mathcal{W}[t] = \mathcal{W}(t, t_1, \mathcal{X}^1) = \{x| \exists u(\cdot) - \text{измеримая, т.ч.} \forall \tau \leqslant t: u(\tau) \in \mathcal{P}(\tau), \exists x^1 \in \mathcal{X}^1: x(t, t_1, x^1| u(\cdot)) = x\} = \underset{x^1 \in \mathcal{X}^1}{\cup}\mathcal{W}(t, t_1, x^1). \]
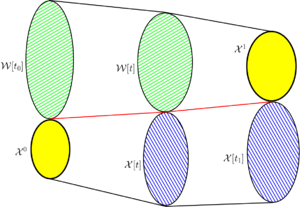
На чертеже приведён пример расположения и изменения множеств достижимости и разрешимости для оптимального времени \(t_1^*\). Красным цветом приведён пример оптимальной траектории движения.
Можно заметить, что для задачи быстродействия "из множества во множество" соответствующие множества достижимости и разрешимости представимы в виде объединений множеств достижижимости/разрешимости по всем точкам начального/конечного множества, т.е. являются обобщениями множеств достижимости и разрешимости для задачи быстродействия "из точки в точку".
Заметим также, что с содержательной точки зрения множество достижимости \(~-\) это множество всех точек в фазовом пространстве, в которых мы можем оказаться в момент времени \(t\), используя всевозможные доступные управления \(u(\cdot)\) и всевозможные точки старта \(x^0\) из начального множества \(\mathcal{X}^0\).
Аналогично, множество разрешимости \(~-\) это множество всех точек в фазовом пространстве, из которых мы можем попасть, стартуя момент времени \(t\) и используя всевозможные доступные управления \(u(\cdot)\) во всевозможные точки финиша \(x^1\) из конечного множества \(\mathcal{X}^1\).
Свойства множеств достижимости и разрешимости
Выпуклость и компактность
Утверждение: Множества достижимости и разрешимости\(~-\) непустые выпуклые компакты.
Доказательство: Заметим, что: \[ \begin{cases} \mathcal{X}\left(t, t_0, \mathcal{X}^0\right) = X(t, t_0)\mathcal{X}^0 + \mathcal{X}(t, t_0, 0), \\ \mathcal{W}\left(t, t_1, \mathcal{X}^1\right) = X(t, t_1)\mathcal{X}^1 + \mathcal{W}(t, t_1, 0), \end{cases} \] где \(X(t, \tau)~-\) фундаментальная матрица Коши. В самом деле, по формуле Коши: \[ x(t) = X(t, t_0)x^0 + \int\limits_{t_0}^{t}X(t, \tau)(B(\tau)u(\tau)+f(\tau))d\tau. \] Тогда в силу определения множества достижимости через объединение по всем допустимым значениям из исходного множества \(\mathcal{X}^0\) и всем допустимым управлениям \(u(\cdot)\) получаем формулу выше. Аналогичным образом поступаем с формулой для множества разрешимости. При решении задачи быстродействия "из точки в точку" доказываются следующие два факта: \[ \begin{cases} \mathcal{X}(t, t_0, 0) \in \text{conv}\mathbb{R}^n, \\ \mathcal{W}(t, t_1, 0) \in \text{conv}\mathbb{R}^n. \end{cases} \] По условию задачи: \(\mathcal{X}^0, \mathcal{X}^1 \in \text{conv}\mathbb{R}^n\). Тогда: \[ X(t, t_0)\mathcal{X}^0 \in \text{conv}\mathbb{R}^n, \\ X(t, t_1)\mathcal{X}^1 \in \text{conv}\mathbb{R}^n. \] Суммируя непустые выпуклые компакты, получаем: \[ \begin{cases} X(t, t_0)\mathcal{X}^0 + \mathcal{X}(t, t_0, 0) \in \text{conv}\mathbb{R}^n, \\ X(t, t_1)\mathcal{X}^1 + \mathcal{W}(t, t_1, 0) \in \text{conv}\mathbb{R}^n, \end{cases} \] что и требовалось доказать.
Критерий оптимальности конечного времени
Утверждение: \(t_1^*~-\) оптимальное конечное время тогда и только тогда, когда \(t_1^*~-\) минимальный корень уравнения (относительно \(t\)): \[ d(\mathcal{X}(t, t_0, \mathcal{X}^0), \mathcal{X}^1) = 0, \] на луче \(t_1 \geqslant t_0\), где \(d(X, Y)~-\) евклидово расстояние между множествами \(X\) и \(Y\).
Доказательство: \(\mathcal{X}^1, \mathcal{X}(t, t_0, \mathcal{X}^0) \in \text{conv} \mathbb{R}^n\). Из курса выпуклого анализа (см. книгу А.В. Арутюнова "Лекции по выпуклому и многозначному анализу", Москва, Физматлит, 2014) [1] известно, что: \[ \forall Z_1, Z_2 \in \text{conv}\mathbb{R}^n: d\left(Z_1, Z_2\right) = 0 \Leftrightarrow \exists z \in Z_1 \cap Z_2. \] Отсюда вытекает критерий оптимальности времени \(t_1^*\).
Теорема фон Неймана о минимаксе
Если выполнены следующие условия: \[ \begin{cases} X, Y - \text{выпуклые компакты}, \\ X \subseteq \mathbb{R}^k, Y \subseteq \mathbb{R}^l, \\ \varphi : X \times Y \rightarrow \mathbb{R} \text{, непрерывна на } X \times Y, \\ \forall y\in Y: \varphi(\cdot, y) -\text{ выпукла по }x, \\ \forall x\in X: \varphi(x, \cdot) -\text{ вогнута по }y, \end{cases} \] то: \[ \underset{x\in X}{\text{inf}}~\underset{y\in Y}{\text{sup}}~\varphi(x, y) = \underset{y\in Y}{\text{sup}}~\underset{x\in X}{\text{inf}}~\varphi(x, y). \] Доказательство теоремы фон Неймана приводится в теоремах 1.3 и 1.1 курса лекций по теории игр и исследованию операций Морозова В.В. [2].
Применение теоремы о минимаксе
Воспользуемся теоремой фон Неймана для получения некоторых результатов по нашей задаче. Пусть \(Z^1, Z^2 \in \text{conv}\mathbb{R}^n\). Тогда: \[ d(Z^1, Z^2) = \text{inf}\left\{||z^1-z^2|| \bigg|~ z^1 \in Z^1, z^2 \in Z^2\right\} = \underset{z^1 \in Z^1}{\text{inf}} d\left(z^1, Z^2\right) = \underset{z^1 \in Z^1}{\text{inf}} \underset{||l|| \leqslant 1}{\text{sup}} \left[<l,z^1> - \rho\left(l \big| Z^2\right)\right]. \] Последнее равенство следует из теории двойственности Фенхеля-Моро, обсуждаемой в курсе выпуклого анализа. Более подробно о ней можно узнать из книги А.В. Арутюнова "Лекции по выпуклому и многозначному анализу"[3]. Применим к правой части последнего равенства теорему о минимаксе. Получим: \[ d(Z^1, Z^2) = \underset{||l|| \leqslant 1}{\text{sup}}\underset{z^1 \in Z^1}{\text{inf}} \left[-<-l,z^1> - \rho\left(l \big| Z^2\right)\right] =\\ =~\underset{||l|| \leqslant 1}{\text{sup}}\left[-\underset{z^1 \in Z^1}{\text{sup}} <-l,z^1> - \rho\left(l \big| Z^2\right)\right] =\\ =~\underset{||l|| \leqslant 1}{\text{sup}}\left[-\rho\left(-l \big| Z^1\right) - \rho\left(l \big| Z^2\right)\right]. \] Тогда из критерия оптимальности конечного времени: \(t_1^* ~-\) минимальный корень уравнений: \begin{equation}\label{z1} \underset{||l|| \leqslant 1}{\text{max}}\left[-\rho\left(-l \big| \mathcal{X}^1\right) - \rho\left(l \big| \mathcal{X}\left(t_1, t_0, \mathcal{X}^0\right)\right)\right] = 0, \end{equation} \begin{equation}\label{z2} \underset{||l|| \leqslant 1}{\text{max}}\left[-\rho\left(-l \big| \mathcal{X}^0\right) - \rho\left(l \big| \mathcal{W}\left(t_0,t_1,\mathcal{X}^1\right)\right)\right] = 0. \end{equation} При этом: \[ (\ref{z1}) \Leftrightarrow \forall l: ~ \left[-\rho\left(-l \big| \mathcal{X}^1\right) - \rho\left(l \big| \mathcal{X}\left(t_1, t_0, \mathcal{X}^0\right)\right)\right] \leqslant 0, \] \[ (\ref{z2}) \Leftrightarrow \forall l: ~ \left[-\rho\left(-l \big| \mathcal{X}^0\right) - \rho\left(l \big| \mathcal{W}\left(t_0,t_1,\mathcal{X}^1\right)\right)\right] \leqslant 0, \] и для \(t_1^* ~ \exists l_1^*, l_2^*: (\ref{z1}), (\ref{z2})\) обращаются в равенство, т.е: \begin{equation}\label{r1} -\rho\left(-l_1^* \big| \mathcal{X}^1\right) = \rho\left(l_1^* \big| \mathcal{X}\left(t_1, t_0, \mathcal{X}^0\right)\right), \end{equation} \begin{equation}\label{r2} -\rho\left(-l_2^* \big| \mathcal{X}^0\right) = \rho\left(l_2^* \big| \mathcal{W}\left(t_0,t_1,\mathcal{X}^1\right)\right). \end{equation} Ниже приведены иллюстрации к уравнениям \((\ref{r1}), (\ref{r2})\).
Принцип максимума Понтрягина
Пусть задана линейная задача быстродействия: \[ \begin{cases} \dot{x}(t) = A(t)x(t) + B(t)u(t), \hspace{5mm} t \in [t_0, +\infty], \\ x(t_0) \in \mathcal{X}_0, x(t_1) \in \mathcal{X}_1, \\ \forall t: u(t) \in \mathcal{P(t)}, \\ (t_1 - t_0) \rightarrow \underset{u}{\text{inf}}. \end{cases} \] Пусть \((x^*(t), u^*(t))~-\) оптимальная пара, \(u^*(t)\) переводит фазовую точку из положения \(x(t_0) \in \mathcal{X}_0\) в положение \(x(t_1) \in \mathcal{X}_1\) за время \(t_1\). Тогда существует непрерывная вектор-функция \(\psi = \psi(t)\), нигде не обращающаяся в нуль и удовлетворяющая следующим условиям: \[ \begin{cases} \dot{\psi(t)} = -A^T(t)\psi(t), & \textbf{ (сопряжённая система)}\\ \langle B^T(t)\psi(t), u^*(t) \rangle \stackrel{\text{п.в.}}{=} \rho(B^T(t)\psi(t) ~|~ \mathcal{P}), & \textbf{ (условие максимума)}\\ \langle \psi(t_0), x(t_0) \rangle = \rho(\psi(t_0) ~|~ \mathcal{X}_0), & \textbf{ (условие трансверсальности в \(\mathcal{X}_0\))}\\ \langle -\psi(t_1), x(t_1) \rangle = \rho(-\psi(t_1) ~|~ \mathcal{X}_1), & \textbf{ (условие трансверсальности в \(\mathcal{X}_1\))} \end{cases} \] где под \(\rho(l|X)\) понимается значение опорной функции множества \(X\) в направлении \(l\).
Доказательство принципа максимума Понтрягина можно найти в книге: Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976 [4].
Список литературы
- Л.C. Понтрягин, В.Г. Болтянский, Р.В. Гамкрелидзе, Е.Ф. Мищенко. "Математическая теория оптимальных процессов". — М.: Наука, 1976,
- В.В. Морозов. Курс лекций "Теория игр и исследование операций": 2021.
- А.В. Арутюнов. "Лекции по выпуклому и многозначному анализу". Москва, Физматлит, 2014