Фундаментальная матрица Коши
Фундаментальная матрица системы линейных однородных дифференциальных уравнений — матрица, столбцы которой образуют фундаментальную систему решений этой системы.
Содержание
Определение
Фундаментальная матрица Коши $$X(t,\tau)$$ — решение задачи Коши \begin{equation} \left\{ \begin{aligned} & \frac{\partial X(t,\tau)}{\partial t} = A(t)X(t,\tau),\\ & X(\tau,\tau) = I. \end{aligned} \right. \end{equation}
$$X(t,\tau) = [x^1(t,\tau),\ldots,x^n(t,\tau)]$$, где $$x^j$$ — решение \[ \left\{ \begin{aligned} & \dot x(t) = A(t)x(t),\\ & x(t_0)=x^0. \end{aligned} \right. \]
Свойства
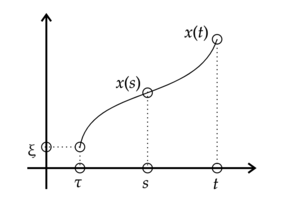
- Полугрупповое свойство: $$X(t,\tau) = X(t,s)X(s,\tau)$$.
$$\left\{ \begin{aligned} & \dot x(t)=A(t)x(t),\\ &x(\tau)=\xi. \end{aligned} \right.$$
$$\qquad \Downarrow$$
$$x(t)=X(t,\tau)\xi \Rightarrow \begin{aligned} & x(t) = X(t,s)x(s)\\ & x(s)=X(s,\tau)\xi \end{aligned}$$
|
$$X(t,\tau)\xi = X(t,s)X(s,\tau)\xi \quad \forall \xi.$$ |
- $$\tau = t$$
$$I=X(t,s)X(s,t)$$
|
$$X(s,t)=X^{-1}(t,s).$$ |
- Рассмотрим $$I=X(t,\tau)X(\tau,t)$$.
Продифференцируем по $$\tau$$: $$0=\frac{\partial X(t,\tau)}{\partial\tau}X(\tau,t)+X(t,\tau)\frac{\partial X(\tau,t)}{\partial\tau}$$. При этом $$\frac{\partial X(\tau,t)}{\partial\tau} = A(\tau)X(\tau,t)$$.
Отсюда следует, что
|
$$\frac{\partial X(t,\tau)}{\partial\tau}=-X(t,\tau)A(\tau)$$. |
- $$S(t,\tau)=X^T(\tau,t)$$
$$\frac{\partial S(t,\tau)}{\partial t}=-A^T(t)S(t,\tau)$$
$$\frac{\partial X(\tau,t)}{\partial t}=-X(\tau,t)A(t)$$
$$\Rightarrow $$
|
$$S(t)=-A^T(t)S(t)$$ - сопряжённая система. |
Система дифференциальных уравнений с постоянными коэффициентами
Рассмотрим неоднородную систему: \[ x'(t) = A(t)x(t)+B(t), \quad x(t)\in\mathbb{R}^n, \] где $$B(t)\in\mathbb{R}^n$$ — локально суммируемая функция.
В случае $$A(t) = A = const$$ матрицант равен $$X(t) = e^{A(t-t_0)},$$ где $$e^{As}$$ — матричная экспонента (см. статью про матричный экспоненциал), следовательно, матрица Коши:
$$C(t,s) = e^{A(t-s)},$$
$$C(t,s) = X(t-s).$$
Таким образом, в этом случае для получения матрицы Коши достаточно подставить $$(t-s)$$ в качестве аргумента матрицанта.
Общее решение системы линейных неоднородных дифференциальных уравнений с постоянными коэффициентами имеет вид:
\[
x(t)=e^{A(t-t_0)}x(t_0)+\int\limits_{t_0}^{t}e^{A(t-s)}B(s)ds.
\]
Пример
Рассмотрим систему $$(1)$$ при $$A = \begin{bmatrix} -2 & 12 \\-1 & 5 \end{bmatrix}$$:
\[
\left\{
\begin{aligned}
& \dot x_1(t) = -2x_1(t) + 12 x_2(t),\\
& \dot x_2(t) = -x_1(t) + 5 x_2(t) + au,\\
& x_1(0) = x_1^0,\\
& x_2(0) = x_2^0,
\end{aligned}
\right.
\]
где $$u$$ — управление, $$a, x_1^0, x_2^0$$ — некоторые константы.
Найдём матричный экспоненциал.
1. Найдём собственные значения и собственные векторы матрицы $$A$$.
\[
\begin{vmatrix}
A - \lambda I
\end{vmatrix}
=
\begin{vmatrix}
-2 -\lambda & 12 \\ -1 & 5-\lambda
\end{vmatrix}
= \lambda^2-3\lambda+2 \Rightarrow \lambda_1=1, \quad \lambda_2=2.
\]
При $$\lambda = 1$$ собственный вектор $$(4,1)^T$$. При $$\lambda = 2$$ собственный вектор $$(3,1)^T$$.
2. Выпишем ФСР.
\[ x(t) = c_1e^{2t} \begin{bmatrix} 3 \\ 1 \end{bmatrix} + c_2e^t \begin{bmatrix} 4 \\ 1 \end{bmatrix}. \]
Найдём константы $$c_1$$ и $$c_2$$.
\[
\left\{ \begin{aligned} 3c_1+4c_2=1, \\ c_1+c_2=0. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=-1, \\& c_2=1. \end{aligned} \right.
\qquad
\left\{ \begin{aligned} 3c_1+4c_2=0, \\ c_1+c_2=1. \end{aligned} \right. \Rightarrow \left\{ \begin{aligned}& c_1=4, \\& c_2=-3. \end{aligned} \right.
\]
\[ \text{Тогда } e^{At} = \begin{bmatrix} -3e^{2t}+4e^t & 12e^{2t}-12e^t \\ -e^{2t}+e^t & 4e^{2t}-3e^t \end{bmatrix}. \]
Далее по формуле Коши найдём $$x_1$$ и $$x_2$$:
\[x(t) = e^{At}x(0) + \int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau.\]
Здесь $$B = \begin{bmatrix} 0 \\ a \end{bmatrix}.$$
Вычислим $$e^{(t-\tau)}B(\tau):$$ $$\begin{bmatrix} a(12e^{2(t-\tau)}-12e^{(t-\tau)}) \\ a(4e^{2(t-\tau)}-3e^{(t-\tau)}) \end{bmatrix}.$$
Проинтегрируем $$\int\limits_0^{t} e^{(t-\tau)}B(\tau)d\tau = \begin{bmatrix} 6a \\ a \end{bmatrix}.$$
Итого получим
\[
\begin{aligned}
& x_1 = x_1^0(-3e^{2t}+4e^t) + x_2^0(12e^{2t}-12e^t)+6a,\\
& x_2 = x_2^0(-e^{2t}+e^t) + x_2^0(4e^{2t}-3e^t)+a.
\end{aligned}
\]
Система дифференциальных уравнений с периодическими коэффициентами
Рассмотрим систему: \begin{equation} x'(t) = A(t)x(t), \quad x(t)\in\mathbb{R}^n. \end{equation}
Здесь $$A(t)$$ — периодическая.
$$A(t+T)=A(t) \quad \forall t, T>0.$$
$$\tilde x[t]=x[t-kT]$$ — траектория (2).
\[
\overset{\cdot}{\tilde x}[t]=\dot x[t-kT]=A(t-kT)x[t-kT]=A(t)\tilde x[t], \quad \forall k\in\mathbb{Z}.
\]
$$x[t]=X(t,t_0)x^0$$. Пусть $$t_0=0$$. Тогда $$x[t]=X(t,0)x^0$$.
\[
X(t+kT,kT)x^0=\tilde x[t+kT]=x[t]=X(t,0)=x^0,\\
\tilde x[kT]=x[0]=x^0.
\]
\[ X(t,0)=X(t+kT,kT)=X(t+kT,0)X(0,kT). \] Тогда
|
$$X(t+kT,0)=X(t,0)X(kT,0)=X(t,0)(X(T,0))^k.$$ |
Переобозначим $$\Phi(t)=X(t,0)$$. Тогда $$\Phi(T)=X(T,0)$$ — матрица монодромии.
|
$$\Phi(t+kT)=\Phi(t)(\Phi(T))^k.$$ |
Теорема Флоке
Если $$A(t+T)\equiv A(t),\quad \forall t.$$
Тогда существует $$\bar A=const\in\mathbb{C}^{n\times m}$$ и $$\psi(t)$$ такие, что $$\psi(t+T)=\psi(t), \quad \forall t,$$ $$|\psi(t)|\not=0$$, $$\psi(t)\in\mathbb{R}^{n\times n}$$ и $$\Phi(t)=\psi(t)e^{\bar At}.$$
Доказательство:
$$\Phi(0)=I=\psi(0).$$ Тогда $$\psi(T)=\psi(0)=I.$$
$$\Phi(T)=\psi(T)e^{\bar At}$$. Отсюда
\begin{equation}
e^{\bar At}=\Phi(T).
\end{equation}
Решением $$(3)$$ является $$\bar A=\frac1{T}\ln\Phi(T),\quad |\Phi(T)|\not=0$$.
\begin{equation}
\psi(t)=\Phi(t)\left(e^{\bar At}\right)^{-1}=\Phi(t)e^{-\bar At}.
\end{equation}
$$\psi(t+T)=\Phi(t+T)e^{-\bar A(t-T)}= \Phi(t)\underbrace{\Phi(T)e^{-\bar AT}}_{=I \text{ в силу } (3)}e^{-\bar At} = \Phi(t)e^{-\bar At}=\psi(t).$$ $$\blacksquare$$
Нахождение
Один из возможных способов нахождения фундаментальной матрицы можно найти на вкладке "Приложение преобразования Лапласа"
Пример применения
Формула Коши для траектории линейной системы \[ \left\{ \begin{aligned} & \dot x(t) = A(t)x(t) + B(t)u(t)+c(t),\\ & x(t_0)=x^0. \end{aligned} \right. \] выглядит следующим образом: \[ x(t)=X(t,t_0)x^0+\int\limits_{t_0}^{t} X(t,\tau)[B(\tau)u(\tau)+c(\tau)]d\tau. \]