Выпуклая функция и ее свойства: различия между версиями
Anita22 (обсуждение | вклад) |
Anita22 (обсуждение | вклад) |
||
| (не показано 30 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
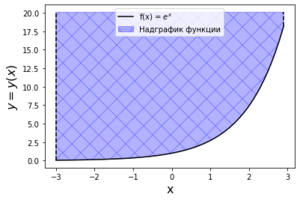
| + | [[Файл:Выпуклая вниз функция.png|300px|thumb|frame|right|Пример выпуклой вниз функции с выпуклым надграфиком.]] | ||
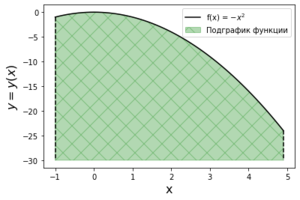
| + | [[Файл:Выпуклая вверх функция.png|300px|thumb|frame|right|Пример выпуклой вверх функции с выпуклым подграфиком.]] | ||
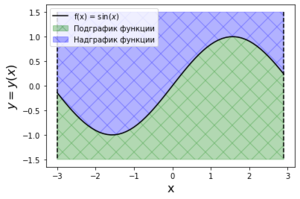
| + | [[Файл:Пример невыпуклой функции.png|300px|thumb|frame|right|Пример невыпуклой функции с надграфиком и подграфиком.]] | ||
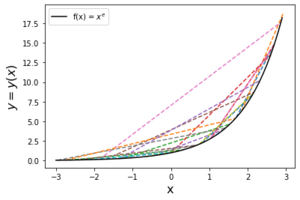
| + | [[Файл:Выпуклая вниз функция2.png|300px|thumb|frame|right|Иллюстрация альтернативного определения выпуклой вниз функции.]] | ||
| − | [[ | + | '''Определение 1.''' ''Выпуклая'' (или ''выпуклая вниз'') функция — функция $$f: X \to \overline{\R}$$, действующая из вещественного линейного пространства $$X \subset \overline{\mathbb{R}}$$ в вещественную расширенную прямую $$\overline{\R} = \{ -\infty\} \cup \R \cup \{ +\infty\}$$, надграфик которой является [[Выпуклое множество и его свойства|выпуклым множеством]]. |
| − | ''' | + | '''Альтернативное определение 1.''' Функция $$f(x)$$, определенная на выпуклом множестве $$X \subset \overline{\mathbb{R}}$$, называется ''выпуклой'', если для всех $$\alpha \in [0, 1]$$ выполняется неравенство: |
| + | \begin{gather*} | ||
| + | f(\alpha x_1 + (1-\alpha)x_2)\leqslant \alpha f(x_1) + (1-\alpha)f(x_2). | ||
| + | \end{gather*} | ||
== Определение выпуклой, собственной функции == | == Определение выпуклой, собственной функции == | ||
| − | + | Пусть $$\overline{\R} = \{ -\infty\} \cup \R \cup \{ +\infty\}$$ — расширенная вещественная прямая, $$X \in \overline{\mathbb{R}}$$ — вещественное линейное пространство. | |
С каждой функцией $$f: X \to \overline{\R}$$ можно связать множества | С каждой функцией $$f: X \to \overline{\R}$$ можно связать множества | ||
\begin{gather*} | \begin{gather*} | ||
| Строка 13: | Строка 20: | ||
называемые соответственно ''надграфиком'' функции $$f$$ и её ''эффективным множеством''. | называемые соответственно ''надграфиком'' функции $$f$$ и её ''эффективным множеством''. | ||
| − | |||
| − | 3. Функция $$f$$ называется | + | '''Определение 2.''' Функция $$f$$ называется ''выпуклой'' (''строго выпуклой''), если ее надграфик $$\operatorname{epi} f$$ является (строго выпуклым), выпуклым множеством. Функция $$f$$ называется ''вогнутой'' или ''выпуклой вверх'' (''строго вогнутой''), если функция $$(−f)$$ является выпуклой (строго выпуклой). |
| + | |||
| + | '''Определение 3.''' Функция $$f$$ называется ''собственной'', если $$\operatorname{dom} f \not= \varnothing$$ и $$f(x) > -\infty$$ для $$\forall x$$. Функция, не являющаяся собственной, называется ''несобственной''. | ||
== Критерии выпуклости функции == | == Критерии выпуклости функции == | ||
=== Неравенство Йенсена === | === Неравенство Йенсена === | ||
| − | ''' | + | '''Теорема (необходимое и достаточное условие выпуклости)'''. Собственная функция $$f$$ является выпуклой $$\Leftrightarrow $$ для $$\forall \alpha \in [0,1]$$, $$\forall x_1, x_2$$ выполняется: |
\begin{gather}\label{eq1} | \begin{gather}\label{eq1} | ||
f(\alpha x_1 + (1-\alpha)x_2) \leqslant \alpha f(x_1) + (1-\alpha)f(x_2). | f(\alpha x_1 + (1-\alpha)x_2) \leqslant \alpha f(x_1) + (1-\alpha)f(x_2). | ||
\end{gather} | \end{gather} | ||
| − | Если это неравенство является строгим для $$\forall \alpha \in | + | Если это неравенство является строгим для $$\forall \alpha \in (0,1)$$ и $$x_1 \neq x_2$$, функция строго выпуклая; если выполняется обратное неравенство, функция вогнутая. |
'''Теорема (неравенство Йенсена)'''. Равенство $$\eqref{eq1}$$, а значит, и выпуклость собственной функции $$f$$, равносильны тому, что для $$\forall n \in \N$$ имеет место неравенство: | '''Теорема (неравенство Йенсена)'''. Равенство $$\eqref{eq1}$$, а значит, и выпуклость собственной функции $$f$$, равносильны тому, что для $$\forall n \in \N$$ имеет место неравенство: | ||
| Строка 31: | Строка 39: | ||
\forall (\alpha_1,..., \alpha_n): \: | \forall (\alpha_1,..., \alpha_n): \: | ||
\sum_{i=1}^n\alpha_i = 1, \: | \sum_{i=1}^n\alpha_i = 1, \: | ||
| − | \alpha_i \ | + | \alpha_i \geqslant 0, |
\end{gather} | \end{gather} | ||
для любых точек $$x_1, ..., x_n$$. | для любых точек $$x_1, ..., x_n$$. | ||
| Строка 54: | Строка 62: | ||
| − | '''Лемма'''. Пусть $$X$$ | + | '''Лемма'''. Пусть $$X$$ — нормированное пространство, функция $$f: X \to \R$$, непрерывна и |
\begin{gather*} | \begin{gather*} | ||
| − | f \left( \dfrac{x+y}{2} \right) \leqslant \frac{f \left( x \right) + f \left( y \right)}{2} | + | f \left( \dfrac{x+y}{2} \right) \leqslant \frac{f \left( x \right) + f \left( y \right)}{2} |
\end{gather*} | \end{gather*} | ||
| − | т. е. неравенство Йенсена выполняется лишь при $$\alpha = 1/2$$. Тогда функция $$f$$ выпукла. | + | $$\forall x, y \in X$$, т. е. неравенство Йенсена выполняется лишь при $$\alpha = 1/2$$. Тогда функция $$f$$ выпукла. |
| − | ''Доказательство''. Докажем по индукции, что для $$\forall \alpha = \dfrac{m}{2^k}\in (0,1)$$ выполняется неравенство Йенсена $$f(\alpha x + (1- \alpha)y) \leqslant \alpha f(x) + (1-\alpha) f(y)$$. | + | ''Доказательство''. Докажем по индукции по $$k$$, что для $$\forall \alpha = \dfrac{m}{2^k}\in (0,1)$$ выполняется неравенство Йенсена $$f(\alpha x + (1- \alpha)y) \leqslant \alpha f(x) + (1-\alpha) f(y)$$. |
| − | 1. Подставим $$\alpha_1 = 3/4$$ и $$\alpha_2 = 1/4$$ в неравенство Йенсена $$\eqref{eq2}$$. | + | 1. База индукции при $$k=2$$. Подставим $$\alpha_1 = 3/4$$ и $$\alpha_2 = 1/4$$ в неравенство Йенсена $$\eqref{eq2}$$. |
\begin{gather*} | \begin{gather*} | ||
f \left( \dfrac{3}{4}x + \dfrac{1}{4}y \right) \leqslant | f \left( \dfrac{3}{4}x + \dfrac{1}{4}y \right) \leqslant | ||
| Строка 82: | Строка 90: | ||
\end{gather*} | \end{gather*} | ||
| − | 3. Докажем, что функция $$f$$ выпукла, т. е. неравенство Йенсена | + | 3. Докажем, что функция $$f$$ выпукла, т. е. неравенство Йенсена выполняется для произвольных $$\alpha, \beta \in [0, 1]$$, $$\alpha + \beta = 1$$. Выберем $$\{\alpha_n, \beta_n\}$$ вида $$\alpha_n = \dfrac{m}{2^k}$$ так, что $$\{\alpha_n, \beta_n\} \to \{\alpha, \beta\}$$ при $$n \to \infty$$. Из непрерывности $$f$$ следует $$f(\alpha_n x + \beta_n y) \to f(\alpha x + \beta y)$$ при $$n \to \infty$$. |
В силу доказанного в п. 2 для $$\forall n$$: | В силу доказанного в п. 2 для $$\forall n$$: | ||
| Строка 95: | Строка 103: | ||
$$\blacksquare$$ | $$\blacksquare$$ | ||
| − | Если функция (не обязательно собственная) выпукла, то $$\eqref{eq2}$$ выполняется для любого набора точек $$x_1,...,x_n$$, для которых $$-\infty < f(x_i) < +\infty$$, $$i = \overline{1, n}$$. | + | '''Замечание 1.''' Если функция (не обязательно собственная) выпукла, то $$\eqref{eq2}$$ выполняется для любого набора точек $$x_1,...,x_n$$, для которых $$-\infty < f(x_i) < +\infty$$, $$i = \overline{1, n}$$. |
| + | '''Замечание 2.''' Если функции $$f$$, $$g$$ выпуклы, то любая их линейная комбинация $$af+bg$$ с положительными коэффициентами $$a, b \in \R$$ также выпукла. | ||
| + | '''Замечание 3.''' Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом). | ||
| − | + | Далее считаем, что $$X$$ — нормированное пространство. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Далее считаем, что $$X$$ | ||
=== Критерий выпуклости === | === Критерий выпуклости === | ||
| − | ''Аффинной оболочкой множества'' $$A \subset X$$ ($$\operatorname{aff} A$$) называется множество всевозможных аффинных комбинаций точек из $$A$$, то есть | + | '''Определение 4.''' ''Аффинной оболочкой множества'' $$A \subset X$$ ($$\operatorname{aff} A$$) называется множество всевозможных аффинных комбинаций точек из $$A$$, то есть |
\begin{gather*} | \begin{gather*} | ||
| − | \operatorname{aff} A = \left\{ x: x = \sum_{i = 1}^n \alpha_i x_i \ | + | \operatorname{aff} A = \left\{ x: x = \sum_{i = 1}^n \alpha_i x_i \left| n \in \N, \; \sum_{i=1}^n \alpha_i = 1, \; x_i \in A \right. \right\}. |
\end{gather*} | \end{gather*} | ||
| − | Пусть $$X$$ | + | '''Определение 5.''' Пусть $$X$$ — нормированное пространство, и $$A \subset X$$. ''Относительной внутренностью выпуклого множества'' $$A$$ ($$\operatorname{ri} A$$) называется внутренность $$A$$ относительно $$\operatorname{aff} A$$. А именно, точка $$x_0 \in \operatorname{ri} A$$, если $$\exists ε > 0$$ такое, что |
| − | ''Относительной внутренностью выпуклого множества'' $$A$$ ($$\operatorname{ri} A$$) называется внутренность $$A$$ относительно $$\operatorname{aff} A$$. А именно, точка $$x_0 \in \operatorname{ri} A$$, если $$\exists ε > 0$$ такое, что | ||
\begin{gather*} | \begin{gather*} | ||
O(x_0, ε) \cap \operatorname{aff A} \subset A. | O(x_0, ε) \cap \operatorname{aff A} \subset A. | ||
\end{gather*} | \end{gather*} | ||
| − | '''Теорема'''. Пусть множество $$A \subset \R^n$$ выпукло. Тогда его относительная | + | '''Пример.''' Отрезок на плоскости имеет пустую внутренность, но его относительная внутренность — тот же отрезок без концов. |
| + | |||
| + | '''Теорема'''. Пусть множество $$A \subset \R^n$$ выпукло. Тогда его относительная внутренность $$\operatorname{ri} A$$ непуста. | ||
'''Лемма 1'''. Пусть выпуклая функция $$f$$ не является собственной. Тогда | '''Лемма 1'''. Пусть выпуклая функция $$f$$ не является собственной. Тогда | ||
| Строка 126: | Строка 132: | ||
Иными словами, несобственная выпуклая функция бесконечна во всех точках, кроме, быть может, точек относительной границы своего эффективного множества. | Иными словами, несобственная выпуклая функция бесконечна во всех точках, кроме, быть может, точек относительной границы своего эффективного множества. | ||
| − | '''Лемма 2'''. Пусть $$f$$ | + | '''Лемма 2'''. Пусть $$f$$ — выпуклая функция и $$X \in \R^n$$. Тогда $$a \in \R^n$$, $$b \in \R$$ что: |
\begin{gather*} | \begin{gather*} | ||
f(x) \geqslant \langle a, x\rangle+b \; \forall x \in X. | f(x) \geqslant \langle a, x\rangle+b \; \forall x \in X. | ||
\end{gather*} | \end{gather*} | ||
| − | '''Теорема (критерий выпуклости)'''. Пусть $$X$$ | + | '''Теорема (критерий выпуклости)'''. Пусть $$X$$ — евклидово пространство и функция $$f$$ дважды непрерывно дифференцируема на $$X$$. Тогда функция $$f$$ выпуклая $$\Leftrightarrow $$ для $$\forall x \in X$$ выполняется: |
\begin{gather}\label{eq3} | \begin{gather}\label{eq3} | ||
\dfrac{\partial^2 f(x)}{\partial x^2} \geqslant 0 \; | \dfrac{\partial^2 f(x)}{\partial x^2} \geqslant 0 \; | ||
| Строка 137: | Строка 143: | ||
Здесь неотрицательность квадратичной формы $$Q = \frac{\partial^2 f(x)}{\partial x^2}$$ означает, что $$\langle Qξ, ξ\rangle \geqslant 0 \forall ξ \in X $$. | Здесь неотрицательность квадратичной формы $$Q = \frac{\partial^2 f(x)}{\partial x^2}$$ означает, что $$\langle Qξ, ξ\rangle \geqslant 0 \forall ξ \in X $$. | ||
| − | ''Доказательство. Необходимость''. Обозначим $$ \dfrac{\partial^2 f(x)}{\partial x^2} = f''(x)$$. Предположим, | + | ''Доказательство. Необходимость''. Обозначим $$ \dfrac{\partial^2 f(x)}{\partial x^2} = f''(x)$$. Предположим, функция $$f$$ выпукла. Фиксируем произвольные $$x, y \in X$$. В силу определения выпуклости $$\forall \lambda \in [0, 1]$$ |
\begin{gather*} | \begin{gather*} | ||
f(\lambda x + (1-\lambda)y) \leqslant \lambda f(x) + (1 - \lambda)f(y), | f(\lambda x + (1-\lambda)y) \leqslant \lambda f(x) + (1 - \lambda)f(y), | ||
| Строка 153: | Строка 159: | ||
λf(x) \geqslant λf(y) + \langle f'(y + θ_λλ(x-y)), λ(x-y)\rangle. | λf(x) \geqslant λf(y) + \langle f'(y + θ_λλ(x-y)), λ(x-y)\rangle. | ||
\end{gather*} | \end{gather*} | ||
| − | Делим | + | Делим обе части неравенства на $$λ > 0$$, при $$\lambda \to 0+$$ имеем |
\begin{gather*} | \begin{gather*} | ||
f(x) \geqslant f(y) + \langle f'(y), x-y\rangle. | f(x) \geqslant f(y) + \langle f'(y), x-y\rangle. | ||
| Строка 161: | Строка 167: | ||
f(y) \geqslant f(x) + \langle f'(x), y-x\rangle. | f(y) \geqslant f(x) + \langle f'(x), y-x\rangle. | ||
\end{gather*} | \end{gather*} | ||
| − | Складываем | + | Складываем полученные неравенства. |
\begin{gather*} | \begin{gather*} | ||
\langle f'(y) - f'(x), y-x\rangle \geqslant 0 \; \forall x, y. | \langle f'(y) - f'(x), y-x\rangle \geqslant 0 \; \forall x, y. | ||
\end{gather*} | \end{gather*} | ||
| − | Пусть $$y=x+\ | + | Пусть $$y=x+\varepsilon h$$ и $$\varepsilon > 0$$. Повторяя рассуждения, основанные на применении [https://ru.wikipedia.org/wiki/%D0%A4%D0%BE%D1%80%D0%BC%D1%83%D0%BB%D0%B0_%D0%BA%D0%BE%D0%BD%D0%B5%D1%87%D0%BD%D1%8B%D1%85_%D0%BF%D1%80%D0%B8%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D0%B9 формулы конечных приращений Лагранжа], получаем, что для $$\forall \varepsilon > 0$$ $$\exists \overline{θ_ε} \in [0,1]$$ такое, что |
\begin{gather*} | \begin{gather*} | ||
\langle f''(x + εh)εh, εh\rangle \geqslant 0. | \langle f''(x + εh)εh, εh\rangle \geqslant 0. | ||
| Строка 196: | Строка 202: | ||
\end{gather*} | \end{gather*} | ||
| + | '''Замечание'''. Обратное, в общем случае, неверно. Например, функция $$f(x) = -x^4$$ не выпукла на $$[-1, 1]$$, но её вторая производная в точке $$x = 0$$ равна 0. | ||
| + | |||
| + | == Замкнутость, ограниченность, непрерывность и липшицевость выпуклых функций == | ||
| + | '''Определение 6.''' Будем считать, что $$X$$ — нормированное пространство. Функция $$f: X \to \overline{\R}$$ ''непрерывна в точке $$x_0 \in X$$'', если для любой сходящейся к ней последовательности $$\bigl\{x_i\bigr\}$$ имеет место $$f(x_i) \rightarrow f(x_0)$$ при $$i \rightarrow \infty$$. | ||
| + | |||
| + | '''Определение 7.''' Определенная на $$X$$ функция $$f$$ называется ''полунепрерывной снизу в точке $$x_0$$'', если $$\underline{\lim}_{x_i \rightarrow x_0} f(x_i) \geqslant f(x_0)$$. Функция $$f$$ называется ''полунепрерывной сверху в точке $$x_0$$'', если функция $$-f$$ полунепрерывна снизу. Функция ''полунепрерывна снизу (сверху)'', если она полунепрерывна снизу (сверху) во всех точках. | ||
| − | '' | + | '''Определение 8.''' Функция называется ''замкнутой'', если её надграфик замкнут. |
| − | == | + | '''Замечание'''. Пусть $$f$$ — выпуклая собственная функция и $$X = \overline{\R}^n$$. Тогда её замыкание $$\operatorname{cl} f$$ также является собственной функцией. |
| − | + | ||
| + | === Полунепрерывность снизу и замкнутость множества Лебега === | ||
| + | |||
| + | '''Определение 9.''' ''Множеством Лебега'' назовем $$\mathcal{L}_a f = \{ x \in X | f(x) \leqslant a \}.$$ | ||
| + | |||
| + | '''Теорема (критерий полунепрерывности снизу)'''. Функция $$f$$ полунепрерывна снизу $$\Leftrightarrow$$, когда для $$\forall a \in \R$$ ее множество Лебега $$\mathcal{L}_a f$$ замкнутое. | ||
| + | |||
| + | ''Доказательство. Необходимость''. Пусть $$f$$ полунепрерывна снизу. Рассмотрим предельную точку $$x_0$$ $$\{x_k\} \subset \mathcal{L}_a f$$. В силу полунепрерывности снизу имеем | ||
| + | \begin{gather*} | ||
| + | f(x_0) \leqslant \underline{\lim}_{x_k \to x_0} f(x_k) \leqslant a \Rightarrow f(x_0) \leqslant a \Rightarrow x_0 \in \mathcal{L}_a f, | ||
| + | \end{gather*} | ||
| + | что доказывает замкнутость множества Лебега $$\mathcal{L}_a f$$. | ||
| + | ''Достаточность''. Докажем от противного. Предположим $$\exists x_0$$, в которой функция $$f$$ не является полунепрерывной снизу. Тогда $$\{x_k\} \to x_0$$, что | ||
| + | \begin{gather*} | ||
| + | b = \lim_{x_k \to x_0}f(x_k) < f(x_0). | ||
| + | \end{gather*} | ||
| + | Выберем число $$a$$ так, что $$b<a<f(x_0)$$. Тогда $$x_k \in \mathcal{L}_a f$$ для всех достаточно больших $$k$$, откуда в силу замкнутости $$\mathcal{L}_a f$$ имеем $$x_0 \in \mathcal{L}_a f$$. Но по построению $$f(x_0)>a$$. Полученное противоречие завершает рассуждения. | ||
| + | $$\blacksquare$$ | ||
| + | |||
| + | === Замкнутость === | ||
| + | '''Теорема (критерий замкнутости)'''. Для замкнутости функции необходимо и достаточно, чтобы она была полунепрерывна снизу. | ||
| + | |||
| + | ''Доказательство. Необходимость.'' Пусть функция $$f$$ замкнута. Рассмотрим множество Лебега $$\mathcal{L}_a f$$ и лежащую в нем последовательность точек $$\{x_i\}$$, которая сходится к точке $$x_0$$. Тогда | ||
| + | \begin{gather*} | ||
| + | f(x_i) a \Rightarrow (x_i, a) \in \operatorname{epi} f, \; (x_i, a) \to (x_0, a). | ||
| + | \end{gather*} | ||
| + | Из определения замкнутости $$f$$ следует, что $$(x_0,a) \in \operatorname{epi} f \Rightarrow f(x_0) \leqslant a \Rightarrow x_0 \in \mathcal{L}_a f$$. Таким образом, доказано, что все множества Лебега функции $$f$$ замкнуты, откуда вытекает, что она полунепрерывна снизу. | ||
| + | ''Достаточность''. Пусть функция $$f$$ полунепрерывна снизу. Рассмотрим последовательность точек $$(x_i, a_i) \in \operatorname{epi} f$$, и пусть $$(x_i, a_i) \to (x_0, a_0)$$, $$i \to \infty$$. Для доказательства замкнутости функции $$f$$ нужно показать, что $$(x_0, a_0) \in \operatorname{epi} f$$. Докажем от противного, т.е. что $$(x_, a_0) \not \in \operatorname{epi} f$$. Тогда $$f(x_0)>a_0$$. | ||
| − | + | Выберем число γ такое, что $$a_0 < γ< f(x_0)$$. Тогда $$x_0 \not\in \mathcal{L}_γ f$$ и, значит, $$\existsε>0$$ такое, что $$O(x_0, ε)\cap\mathcal{L}_γ f = \varnothing$$, поскольку множества Лебега полунепрерывной снизу функции замкнуты. Поэтому для всех достаточно больших $$i$$ имеем $$x_i \not\in \mathcal{L}_γ f$$, откуда $$f(x_i)>γ$$. Поскольку $$γ>a_0$$, неравенство $$f(x_i)>a_i$$ справедливо для всех достаточно больших $$i$$, а это противоречит тому, что $$(x_0, a_0) \in \operatorname{epi} f$$. | |
| + | $$\blacksquare$$ | ||
| − | + | ''Замечание''. Мы показали, что следующие 3 свойства функции равносильны: | |
| − | + | 1. полунепрепрерывность снизу, | |
| − | + | 2. замкнутость всех её множеств Лебега, | |
| − | |||
| − | + | 3. замкнутость самой функции. | |
| − | |||
=== Полунепрерывность сверху === | === Полунепрерывность сверху === | ||
| − | Пусть $$f: \R^n \to \overline{\R}$$ | + | '''Определение 10.''' Множество $$M$$ будем называть ''симплектическим'', если его можно представить в виде объединения конечного числа [https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D0%BC%D0%BF%D0%BB%D0%B5%D0%BA%D1%81 симплексов] ($$n$$-мерных обобщений треугольника). |
| − | То есть, если последовательность $$$$ $$M$$ $$x_0$$, то верхний предел $$f(x_i)$$ не превышает $$f(x_0)$$. | + | |
| + | '''Определение 11.''' Пусть система векторов $$x_i \in \R^n, \; i = \overline{0, n}$$, аффинно независима, тогда любой вектор $$x \in \R^n$$ можно представить в виде $$x = \sum_{i=0}^n \alpha^ix_i, \; \sum_{i=0}^n \alpha^i = 1$$, причем это представление единственно. Числа $$\alpha^0,.. \alpha^n$$ называются ''барицентрическими координатами'' точки $$x$$ относительно системы $$x_0,...,x_n$$. | ||
| + | |||
| + | Пусть $$L=\{\alpha = (\alpha^0,.. \alpha^n) \in \R^{n+1}: \sum_{i=0}^n \alpha^i = 1\}$$ — линейное многообразие. Определим отображение $$\alpha: \R^n \to L$$, где $$\alpha(x)=(\alpha^0,.. \alpha^n)$$ — [https://ru.wikipedia.org/wiki/%D0%91%D0%B0%D1%80%D0%B8%D1%86%D0%B5%D0%BD%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D0%BA%D0%BE%D0%BE%D1%80%D0%B4%D0%B8%D0%BD%D0%B0%D1%82%D1%8B барицентрические координаты] точки $$x_i \in \R^n$$ относительно аффинно независимой системы $$x_0,...,x_n$$. | ||
| + | |||
| + | '''Теорема'''. Отображение $$\alpha(\cdot)$$ непрерывное. | ||
| + | |||
| + | '''Теорема о полунепрерывности сверху'''. Пусть $$f: \R^n \to \overline{\R}$$ — выпуклая функция и $$M \subset \operatorname{dom} f$$ — симплектическое множество. Тогда сужение $$f$$ на $$M$$ полунепрерывно сверху. | ||
| + | То есть, если последовательность $$\{x+i\}$$ лежит во множестве $$M$$ и сходится к точке $$x_0$$, то верхний предел $$f(x_i)$$ не превышает $$f(x_0)$$. | ||
| + | |||
| + | ''Доказательство''. Достаточно рассмотреть только случай, когда само $$M$$ является $$n$$-мерным симплексом. Возьмем точку $$x_0 \in M$$ и докажем, что сужение $$f$$ полунепрерывно сверху в этой точке. | ||
| + | |||
| + | Осуществим барицентрическое подразделение ([https://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B0%D0%BD%D0%B3%D1%83%D0%BB%D1%8F%D1%86%D0%B8%D1%8F_(%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F) триангуляцию]) симплекса $$M$$ следующим образом. Возьмем какую-нибудь $$(n-1)$$-мерную грань $$Γ_i$$ симплекса $$M$$ (т.е. выпуклую оболочку его $$n$$ вершин) и положим $$M_i = \operatorname{conv}(Γ_i \cup \{x_0\})$$. Таким образом, исходный симплекс представим в виде объединения $$(n+1)$$ симплексов $$M_i$$, у каждого из которых $$x_0$$ является вершиной, и нам достаточно доказать, что $$f$$ полунепрерывна сверху на $$\forall Mi$$. | ||
| + | |||
| + | Не теряя общности считаем, что исходный симплекс $$M = \operatorname{conv}\{x_0,...,x_n\}$$. Для удобства $$x_0 = 0$$. | ||
| + | |||
| + | Произвольная точка $$x \in M$$ $$x = \sum_{i=0}^n \alpha^i(x)x_i$$, где $$\alpha(x) = (\alpha^0(x), ..., \alpha^n(x)))$$ — барицентрические координаты точки $$x$$. По теореме 1 отображение $$\alpha$$ непрерывно. Поэтому при $$x \to 0$$ имеет место $$\alpha^0(x) \to 1, \; \alpha^i(x) \to 0 \; i = 1,...,n$$. В силу выпуклости функции $$f$$ имеем | ||
| + | |||
| + | \begin{gather*} | ||
| + | f(x_i) = f \bigl(\sum_{i=0}^n \alpha^i(x)x_i\bigr) \leqslant \sum_{i=0}^n \alpha^i(x)f(x_i) = \alpha^0(x)f(0) + \sum_{i=1}^n \alpha^i(x)f(x_i), | ||
| + | \end{gather*} | ||
| + | где, с учетом принятого соглашения, для тех номеров $$i$$, для которых $$\alpha^i(x) = 0, \; f(x_i) = -\infty$$, мы полагаем $$\alpha^i(x)f(x_i)=0$$. Из полученного неравенства заключаем, что верхний предел функции $$f$$ при $$x \to 0, \; x \in M$$ не превышает $$f(0)$$, что завершает доказательство полунепрерывности сверху сужения $$f$$ на $$M$$ в точке $$x_0$$. | ||
| + | $$\blacksquare$$ | ||
| + | |||
| + | |||
| + | |||
| + | === Непрерывность в окрестности точки === | ||
| + | '''Теорема о полунепрерывности в окрестности точки'''. Пусть выпуклая собственная функция $$f: X \to \overline{\R}$$ ограничена сверху в некоторой окрестности заданной точки $$x_0$$. Тогда $$f$$ непрерывна в этой окрестности точки $$x_0$$. | ||
| + | |||
| + | ''Доказательство.'' Не ограничивая общности, считаем $$f(0) = 0$$, $$x_0$$. Выберем числа $$c>0$$ и $$\delta > 0$$ так, что $$f(x) \leq x$$ для $$\forall x \in Q = Q_{\delta}$$. Очевидно, $$Q=-Q$$. | ||
| + | |||
| + | Достаточно доказать, что для $$\forall \varepsilon > 0$$ имеет место $$|f(x)|\leq \varepsilon$$ для $$\forall x \in V_{\varepsilon} = \frac{\varepsilon}{c}Q$$. Зафиксируем произвольное $$\varepsilon \in (0,c)$$ и положим $$V = V_{\varepsilon}$$. Очевидно, $$V = -V$$. В силу выпуклости $$f$$ имеем | ||
| + | \begin{gather} | ||
| + | x = \frac{\varepsilon}{c}\frac{c}{\varepsilon}x + \left(1-\frac{\varepsilon}{c}\right)0 \in V, | ||
| + | \end{gather} | ||
| + | \begin{gather} | ||
| + | f(x) \leq \frac{\varepsilon}{c}f\left(\frac{c}{\varepsilon}x\right) + \left(1 - \frac{\varepsilon}{c}\right)f(0) | ||
| + | \end{gather} | ||
| + | \begin{gather} | ||
| + | f(x) \leq \frac{\varepsilon}{c}f\left(\frac{c}{\varepsilon}x\right) \leq \frac{\varepsilon}{c} c \Longrightarrow f(x) \leq \varepsilon. | ||
| + | \end{gather} | ||
| + | Далее: | ||
| + | \begin{gather} | ||
| + | x \in V = -V = -\frac{\varepsilon}{c}Q \Longrightarrow \left(-x\frac{c}{\varepsilon} \right) \in Q, | ||
| + | \end{gather} | ||
| + | \begin{gather} | ||
| + | 0 = \frac{1}{1+\varepsilon/c}x + \frac{\varepsilon/c}{1+\varepsilon/c}\left(-x\frac{c}{\varepsilon} \right). | ||
| + | \end{gather} | ||
| + | Отсюда в силу выпуклости функции $$f$$ получаем | ||
| + | \begin{gather} | ||
| + | 0 = f(0) \ leq \frac{1}{1+\varepsilon/c}f(x) + \frac{\varepsilon/c}{1+\varepsilon/c}f\left(-x\frac{c}{\varepsilon} \right) \leq \frac{1}{1+\varepsilon/c}f(x) + \frac{\varepsilon}{1+\varepsilon/c} \Longrightarrow f(x) \geq \varepsilon. | ||
| + | \end{gather} | ||
| + | $$\blacksquare$$ | ||
| − | |||
| − | |||
''' Следствие (липшицевость в окрестности)'''. Пусть для выпуклой собственной функции $$f: X \to \overline{\R}$$ и точки $$x_0 \in X$$ $$\exists c > 0$$, $$\delta >0$$, что $$f(x) \leqslant c$$ $$\forall x \in O(x_0, 2\delta)$$. Тогда на множестве $$O(x_0, 2\delta)$$ функция $$f$$ удовлетворяет условию Липшица с константой $$c$$: | ''' Следствие (липшицевость в окрестности)'''. Пусть для выпуклой собственной функции $$f: X \to \overline{\R}$$ и точки $$x_0 \in X$$ $$\exists c > 0$$, $$\delta >0$$, что $$f(x) \leqslant c$$ $$\forall x \in O(x_0, 2\delta)$$. Тогда на множестве $$O(x_0, 2\delta)$$ функция $$f$$ удовлетворяет условию Липшица с константой $$c$$: | ||
| Строка 229: | Строка 317: | ||
''' Следствие'''. Пусть выпуклая собственная функция $$f: X \to \overline{\R}$$ ограничена сверху на некотором непустом открытом множестве. Тогда она непрерывна на множестве $$\operatorname{int}(\operatorname{dom f}) \not = \varnothing$$. | ''' Следствие'''. Пусть выпуклая собственная функция $$f: X \to \overline{\R}$$ ограничена сверху на некотором непустом открытом множестве. Тогда она непрерывна на множестве $$\operatorname{int}(\operatorname{dom f}) \not = \varnothing$$. | ||
| − | $$\text{int A} | + | $$\text{int A} $$— [https://ru.wikipedia.org/wiki/%D0%92%D0%BD%D1%83%D1%82%D1%80%D0%B5%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C внутренность множества]$$A $$ множество всех внутренних точек множества $$A$$. |
=== Теорема о липшицевости на выпуклом компакте === | === Теорема о липшицевости на выпуклом компакте === | ||
| − | Пусть $$f: \R^n \to \overline{\R}$$ | + | '''Лемма.''' Пусть $$f$$ выпукла, $$S$$ — выпуклый компакт, $$S \subset \operatorname{int}\operatorname{dom f}$$. Тогда $$\exists \varepsilon > 0$$ т.ч. |
| + | \begin{gather} | ||
| + | \varepsilon B + S \subset \operatorname{int}\operatorname{dom f}, | ||
| + | \end{gather} | ||
| + | где $$B$$ — единичный шар в $$X = R^n$$. | ||
| + | |||
| + | ''Доказательство.'' От противного. Пусть $$\exists \{x_i\}:$$ $$x_i \in (B/i + S) \notin \operatorname{int}\operatorname{dom f}.$$ Так как $$ (B/i + S)$$ — последовательность вложенных компактов, то последовательность $$\{x_i\}$$ ограничена. Переходя к подпоследовательности считаем $$x_i \rightarrow x_0$$. Очевидно $$x_0 \in S$$, $$x_0 \notin \operatorname{int}\operatorname{dom f}.$$ Противоречие с условием $$S \subset \operatorname{int}(\operatorname{dom f})$$. Значит, такой $$\varepsilon$$ существует. | ||
| + | $$\blacksquare$$ | ||
| + | |||
| + | |||
| + | '''Теорема'''. Пусть $$f: \R^n \to \overline{\R}$$ — собственная выпуклая функция, $$S$$ - выпуклый компакт и $$S \subset \operatorname{int}(\operatorname{dom f})$$. Тогда на множестве $$S$$ функция $$f$$ удовлетворяет условию Липшица. | ||
| + | |||
| + | ''Доказательство.'' 1. Обозначим $$m = \min_{x \in B + S} f(x)$$, $$M = \max_{x \in B + S} f(x)$$. Эти величины существуют в силу $$f \in C(\operatorname{dom f})$$. $$\blacksquare$$ | ||
| + | |||
| + | 2. $$\forall x, y \in S$$ положим $$z = y + \varepsilon(y-x)/|y-x|$$. Значит, $$z \in S + \varepsilon B$$. Выражая $$y$$, получим $$y = (1-\lambda)x + \lambda z$$, где $$\lambda = |y-x|/(|y-x| + \varepsilon) = 1 - \varepsilon/(|y-x| + \varepsilon) < 1.$$ | ||
| + | |||
| + | 3. В силу выпуклости $$f$$: | ||
| + | \begin{gather} | ||
| + | f(y) \leqslant (1-\lambda)f(x) + \lambda f(z) = f(x) + \lambda (f(z) - f(x)) \\ | ||
| + | f(y) - f(x) \leqslant \lambda(f(z) - f(x)) = \frac{|y-x|(f(z)-f(x))}{|y-x|+\varepsilon} \leqslant \frac{|y-x|(M-m)}{|y-x|+\varepsilon} \leqslant \frac{M-m}{\varepsilon}|y-x| = C|y-x|, | ||
| + | \end{gather} | ||
| + | Где $$C = (M-m)\varepsilon$$ — константа Липшица. Таким образом, в силу произвольности точек $$x, y \in S$$ выражение | ||
| + | \begin{gather} | ||
| + | |f(x) - f(y)| \leqslant C|x-y| | ||
| + | \end{gather} | ||
| + | выполняется всегда. $$\blacksquare$$ | ||
== Список литературы == | == Список литературы == | ||
| − | 1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004 | + | 1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004; |
| + | |||
2. Фихтенгольц Г. М. "Курс дифференциального и интегрального исчисления." 8-е изд. М.; СПб., 2001; | 2. Фихтенгольц Г. М. "Курс дифференциального и интегрального исчисления." 8-е изд. М.; СПб., 2001; | ||
| + | |||
3. Ильин В. А., Позняк Э. Г. "Основы математического анализа." 6-е изд. М., 2001. Т. 1. | 3. Ильин В. А., Позняк Э. Г. "Основы математического анализа." 6-е изд. М., 2001. Т. 1. | ||
Текущая версия на 16:48, 19 декабря 2023
Определение 1. Выпуклая (или выпуклая вниз) функция — функция $$f: X \to \overline{\R}$$, действующая из вещественного линейного пространства $$X \subset \overline{\mathbb{R}}$$ в вещественную расширенную прямую $$\overline{\R} = \{ -\infty\} \cup \R \cup \{ +\infty\}$$, надграфик которой является выпуклым множеством.
Альтернативное определение 1. Функция $$f(x)$$, определенная на выпуклом множестве $$X \subset \overline{\mathbb{R}}$$, называется выпуклой, если для всех $$\alpha \in [0, 1]$$ выполняется неравенство: \begin{gather*} f(\alpha x_1 + (1-\alpha)x_2)\leqslant \alpha f(x_1) + (1-\alpha)f(x_2). \end{gather*}
Содержание
Определение выпуклой, собственной функции
Пусть $$\overline{\R} = \{ -\infty\} \cup \R \cup \{ +\infty\}$$ — расширенная вещественная прямая, $$X \in \overline{\mathbb{R}}$$ — вещественное линейное пространство. С каждой функцией $$f: X \to \overline{\R}$$ можно связать множества \begin{gather*} \operatorname{epi} f \equiv \bigl\{(x,\alpha) \in X \times \overline{\R} \mid f(x) \leqslant \alpha\bigr\},\\ \operatorname{dom} f \equiv \bigl\{x \in X \mid f(x) \leqslant +\infty\bigr\}, \end{gather*} называемые соответственно надграфиком функции $$f$$ и её эффективным множеством.
Определение 2. Функция $$f$$ называется выпуклой (строго выпуклой), если ее надграфик $$\operatorname{epi} f$$ является (строго выпуклым), выпуклым множеством. Функция $$f$$ называется вогнутой или выпуклой вверх (строго вогнутой), если функция $$(−f)$$ является выпуклой (строго выпуклой).
Определение 3. Функция $$f$$ называется собственной, если $$\operatorname{dom} f \not= \varnothing$$ и $$f(x) > -\infty$$ для $$\forall x$$. Функция, не являющаяся собственной, называется несобственной.
Критерии выпуклости функции
Неравенство Йенсена
Теорема (необходимое и достаточное условие выпуклости). Собственная функция $$f$$ является выпуклой $$\Leftrightarrow $$ для $$\forall \alpha \in [0,1]$$, $$\forall x_1, x_2$$ выполняется: \begin{gather}\label{eq1} f(\alpha x_1 + (1-\alpha)x_2) \leqslant \alpha f(x_1) + (1-\alpha)f(x_2). \end{gather} Если это неравенство является строгим для $$\forall \alpha \in (0,1)$$ и $$x_1 \neq x_2$$, функция строго выпуклая; если выполняется обратное неравенство, функция вогнутая.
Теорема (неравенство Йенсена). Равенство $$\eqref{eq1}$$, а значит, и выпуклость собственной функции $$f$$, равносильны тому, что для $$\forall n \in \N$$ имеет место неравенство: \begin{gather}\label{eq2} f\Big(\sum_{i=1}^n\alpha_i x_i\Big) \leqslant \sum_{i=1}^n\alpha_i f(x_i) \; \forall (\alpha_1,..., \alpha_n): \: \sum_{i=1}^n\alpha_i = 1, \: \alpha_i \geqslant 0, \end{gather} для любых точек $$x_1, ..., x_n$$.
Доказательство. Докажем по индукции.
1. База при $$n = 2$$ верна в силу $$\eqref{eq1}$$.
2. Пусть это верно для $$n$$. Докажем, что это верно для $$n + 1$$.
По условию $$\sum_{k=1}^{n+1}\alpha_k = 1$$. Обозначим $$s_n =\sum_{k=1}^{n}\alpha_k$$.
$$\beta_k = \alpha_k/s_n$$. Тогда $$\sum_{k=1}^{n}\beta_k = \dfrac{1}{s_n}\sum_{k=1}^{n}\alpha_k = \dfrac{s_n}{s_n} = 1$$.
\begin{gather*} \sum_{k=1}^{n+1}\alpha_k f(x_k) = s_n \sum_{k=1}^{n}\beta_k f(x_k) + \alpha_{n+1}f(x_{n+1}) \leqslant \text{(по предположению индукции)}\leqslant \\ \leqslant s_n f \left( \sum_{k=1}^{n}\beta_k x_k \right) + \alpha_{n+1}f(x_{n+1}) \leqslant \text{(так как } s_n + \alpha_{n+1} ) \leqslant f \left( \sum_{k=1}^{n+1}\alpha_k x_k \right) \end{gather*} $$\blacksquare$$
Следствие. Из $$\eqref{eq2}$$ вытекает, что эффективное множество выпуклой функции выпукло.
Лемма. Пусть $$X$$ — нормированное пространство, функция $$f: X \to \R$$, непрерывна и
\begin{gather*}
f \left( \dfrac{x+y}{2} \right) \leqslant \frac{f \left( x \right) + f \left( y \right)}{2}
\end{gather*}
$$\forall x, y \in X$$, т. е. неравенство Йенсена выполняется лишь при $$\alpha = 1/2$$. Тогда функция $$f$$ выпукла.
Доказательство. Докажем по индукции по $$k$$, что для $$\forall \alpha = \dfrac{m}{2^k}\in (0,1)$$ выполняется неравенство Йенсена $$f(\alpha x + (1- \alpha)y) \leqslant \alpha f(x) + (1-\alpha) f(y)$$.
1. База индукции при $$k=2$$. Подставим $$\alpha_1 = 3/4$$ и $$\alpha_2 = 1/4$$ в неравенство Йенсена $$\eqref{eq2}$$. \begin{gather*} f \left( \dfrac{3}{4}x + \dfrac{1}{4}y \right) \leqslant \dfrac{1}{2}\left( f(x) + f \left( \dfrac{x+y}{2} \right)\right) \leqslant \dfrac{3}{4} f(x) + \dfrac{1}{4} f(y). \end{gather*} Аналогично выполняется для $$\alpha_1 = 1/4$$ и $$\alpha_2 = 3/4$$: \begin{gather*} f \left( \dfrac{1}{4}x + \dfrac{3}{4}y \right) \leqslant \dfrac{1}{4} f(x) + \dfrac{3}{4} f(y). \end{gather*}
2. Пусть неравенство верно для $$\alpha_1, \alpha_2 \in (0,1)$$. Тогда \begin{gather*} f \left( \dfrac{1}{2}( \alpha_1 x + (1 - \alpha_1)y + \alpha_2 x + (1 - \alpha_2)y)\right) \leqslant \dfrac{1}{2}\left( f(\alpha_1 x + (1 - \alpha_1)y) + f(\alpha_2 x + (1-\alpha_2)y \right) \leqslant \\ \leqslant \dfrac{\alpha_1 + \alpha_2}{2}f(x) + \dfrac{(1-\alpha_1) + (1-\alpha_2)}{2} f(y). \end{gather*}
3. Докажем, что функция $$f$$ выпукла, т. е. неравенство Йенсена выполняется для произвольных $$\alpha, \beta \in [0, 1]$$, $$\alpha + \beta = 1$$. Выберем $$\{\alpha_n, \beta_n\}$$ вида $$\alpha_n = \dfrac{m}{2^k}$$ так, что $$\{\alpha_n, \beta_n\} \to \{\alpha, \beta\}$$ при $$n \to \infty$$. Из непрерывности $$f$$ следует $$f(\alpha_n x + \beta_n y) \to f(\alpha x + \beta y)$$ при $$n \to \infty$$.
В силу доказанного в п. 2 для $$\forall n$$: \begin{gather*} f ( \alpha_n x + \beta_n y) \leqslant \alpha_n f(x) + \beta_n f(y). \end{gather*}
В силу произвольности $$n$$ при $$n \to\infty$$ получаем \begin{gather*} f ( \alpha x + \beta y) \leqslant \alpha f(x) + \beta f(y). \end{gather*} $$\blacksquare$$
Замечание 1. Если функция (не обязательно собственная) выпукла, то $$\eqref{eq2}$$ выполняется для любого набора точек $$x_1,...,x_n$$, для которых $$-\infty < f(x_i) < +\infty$$, $$i = \overline{1, n}$$.
Замечание 2. Если функции $$f$$, $$g$$ выпуклы, то любая их линейная комбинация $$af+bg$$ с положительными коэффициентами $$a, b \in \R$$ также выпукла.
Замечание 3. Локальный минимум выпуклой функции является также глобальным минимумом (соответственно, для выпуклых вверх функций локальный максимум является глобальным максимумом).
Далее считаем, что $$X$$ — нормированное пространство.
Критерий выпуклости
Определение 4. Аффинной оболочкой множества $$A \subset X$$ ($$\operatorname{aff} A$$) называется множество всевозможных аффинных комбинаций точек из $$A$$, то есть \begin{gather*} \operatorname{aff} A = \left\{ x: x = \sum_{i = 1}^n \alpha_i x_i \left| n \in \N, \; \sum_{i=1}^n \alpha_i = 1, \; x_i \in A \right. \right\}. \end{gather*}
Определение 5. Пусть $$X$$ — нормированное пространство, и $$A \subset X$$. Относительной внутренностью выпуклого множества $$A$$ ($$\operatorname{ri} A$$) называется внутренность $$A$$ относительно $$\operatorname{aff} A$$. А именно, точка $$x_0 \in \operatorname{ri} A$$, если $$\exists ε > 0$$ такое, что \begin{gather*} O(x_0, ε) \cap \operatorname{aff A} \subset A. \end{gather*}
Пример. Отрезок на плоскости имеет пустую внутренность, но его относительная внутренность — тот же отрезок без концов.
Теорема. Пусть множество $$A \subset \R^n$$ выпукло. Тогда его относительная внутренность $$\operatorname{ri} A$$ непуста.
Лемма 1. Пусть выпуклая функция $$f$$ не является собственной. Тогда \begin{gather*} f(x) = - \infty \; \forall x \in \operatorname{ri}(\operatorname{dom}f). \end{gather*} Иными словами, несобственная выпуклая функция бесконечна во всех точках, кроме, быть может, точек относительной границы своего эффективного множества.
Лемма 2. Пусть $$f$$ — выпуклая функция и $$X \in \R^n$$. Тогда $$a \in \R^n$$, $$b \in \R$$ что: \begin{gather*} f(x) \geqslant \langle a, x\rangle+b \; \forall x \in X. \end{gather*}
Теорема (критерий выпуклости). Пусть $$X$$ — евклидово пространство и функция $$f$$ дважды непрерывно дифференцируема на $$X$$. Тогда функция $$f$$ выпуклая $$\Leftrightarrow $$ для $$\forall x \in X$$ выполняется: \begin{gather}\label{eq3} \dfrac{\partial^2 f(x)}{\partial x^2} \geqslant 0 \; \end{gather} Здесь неотрицательность квадратичной формы $$Q = \frac{\partial^2 f(x)}{\partial x^2}$$ означает, что $$\langle Qξ, ξ\rangle \geqslant 0 \forall ξ \in X $$.
Доказательство. Необходимость. Обозначим $$ \dfrac{\partial^2 f(x)}{\partial x^2} = f''(x)$$. Предположим, функция $$f$$ выпукла. Фиксируем произвольные $$x, y \in X$$. В силу определения выпуклости $$\forall \lambda \in [0, 1]$$ \begin{gather*} f(\lambda x + (1-\lambda)y) \leqslant \lambda f(x) + (1 - \lambda)f(y), \end{gather*} откуда \begin{gather}\label{eq4} \lambda f(x) \geqslant \lambda f(y) + [f(y + \lambda(x-y)) - f(y)]. \end{gather} Для каждого фиксированного $$\lambda \in [0, 1]$$ определим скалярную функцию $$φ_{\lambda} : [0, 1] \to \R$$ по формуле $$φ_{\lambda}(θ) = f(y + θλ(x-y))$$. По формуле конечных приращений Лагранжа $$\forall \lambda \in [0, 1]$$ $$\exists θ_λ \in [0,1]$$, такое, что $$φ_{\lambda}(1) - φ_{\lambda}(0) = φ_{\lambda}'(θ_λ)$$. Поэтому, вычисляя производную $$φ_{\lambda}$$ как производную сложной функции, получаем \begin{gather*} f(y + λ(x-y)) - f(y) = \langle f'(y + θ_λλ(x-y)), λ(x-y)\rangle. \end{gather*} Подставляя это выражение в неравенство $$\eqref{eq4}$$, получаем $$\forall \in [0, 1]$$ $$\exists θ_λ \in [0,1]$$: \begin{gather*} λf(x) \geqslant λf(y) + \langle f'(y + θ_λλ(x-y)), λ(x-y)\rangle. \end{gather*} Делим обе части неравенства на $$λ > 0$$, при $$\lambda \to 0+$$ имеем \begin{gather*} f(x) \geqslant f(y) + \langle f'(y), x-y\rangle. \end{gather*} Меняем $$x$$ и $$y$$ местами, получаем \begin{gather*} f(y) \geqslant f(x) + \langle f'(x), y-x\rangle. \end{gather*} Складываем полученные неравенства. \begin{gather*} \langle f'(y) - f'(x), y-x\rangle \geqslant 0 \; \forall x, y. \end{gather*} Пусть $$y=x+\varepsilon h$$ и $$\varepsilon > 0$$. Повторяя рассуждения, основанные на применении формулы конечных приращений Лагранжа, получаем, что для $$\forall \varepsilon > 0$$ $$\exists \overline{θ_ε} \in [0,1]$$ такое, что \begin{gather*} \langle f''(x + εh)εh, εh\rangle \geqslant 0. \end{gather*} Делим обе части этого равенства на $$ε^2 > 0$$ при $$ε \to 0+$$ получаем $$\langle f''(x)h, h\rangle \geqslant 0$$ $$\forall h \in X$$, что и доказывает $$\eqref{eq3}$$, Достаточность. Пусть выполняется $$\eqref{eq3}$$. Зафиксируем произвольные $$x, y \in X$$. Рассматриваем скалярную функцию $$φ(\alpha) = \langle f'(x + \alpha(y-x)), y-x\rangle$$, $$\alpha \in [0,1]$$. Применяя к этой функции формулу конечных приращений Лагранжа, получаем, что $$\exists θ \in [0, 1]$$, что \begin{gather*} \langle f'(y) - f'(x), y-x\rangle = \langle f''(x + θ(y-x))(y-x) - f'(x), y-x\rangle\geqslant 0. \end{gather*} Пусть $$\lambda \in [0, 1]$$. Положим $$z = \lambda x + (1- \lambda)y$$. Тогда $$x-z = (1-\lambda)(x-y)$$, $$y-z = \lambda(y-x)$$. В силу формулы Ньютона - Лейбница имеем \begin{gather*} λf(x) + (1-λ)f(y) - f(λx + (1-λ)y) = λ(f*x( - f(z)) + (1-λ)(f(y) - f(z)) = \\ = λ \int_0^1 \langle f'(z + t(x-z)), x-z\rangle dt + (1-λ)\int_0^1 \langle f'(z + t(y-z)), y-z\rangle dt = \\ = λ(1-λ)\int_0^1 \langle f'(z + t(x-z)) - f'(z + t(y-z)), x-y\rangle dt. \end{gather*} Сделаем замену $$u = z + t(x-z)$$, $$v = z+t(y-z)$$. В силу $$\eqref{eq3}$$ \begin{gather*} \langle f'(u) - f'(v), u-v\rangle \geqslant 0. \end{gather*} Отсюда получаем: \begin{gather*} \langle f'(z+t(x-z)) - f'(z + t(y-z)), x-y\rangle = \geqslant 0 \; \forall t \in [0,1] \end{gather*} и, следовательно, $$λf(x) + (1-λ)f(y) - f(λx + (1-λ)y) \geqslant 0$$, что завершает доказательство выпуклости функции $$f$$. $$\blacksquare$$
Следствие. Если функция $$f$$ выпукла и дважды непрерывно дифференцируема в некоторой окрестности точки $$x_0 \in X$$, то \begin{gather*} \dfrac{\partial^2 f}{\partial x^2}(x_0) \geqslant 0. \end{gather*}
Замечание. Обратное, в общем случае, неверно. Например, функция $$f(x) = -x^4$$ не выпукла на $$[-1, 1]$$, но её вторая производная в точке $$x = 0$$ равна 0.
Замкнутость, ограниченность, непрерывность и липшицевость выпуклых функций
Определение 6. Будем считать, что $$X$$ — нормированное пространство. Функция $$f: X \to \overline{\R}$$ непрерывна в точке $$x_0 \in X$$, если для любой сходящейся к ней последовательности $$\bigl\{x_i\bigr\}$$ имеет место $$f(x_i) \rightarrow f(x_0)$$ при $$i \rightarrow \infty$$.
Определение 7. Определенная на $$X$$ функция $$f$$ называется полунепрерывной снизу в точке $$x_0$$, если $$\underline{\lim}_{x_i \rightarrow x_0} f(x_i) \geqslant f(x_0)$$. Функция $$f$$ называется полунепрерывной сверху в точке $$x_0$$, если функция $$-f$$ полунепрерывна снизу. Функция полунепрерывна снизу (сверху), если она полунепрерывна снизу (сверху) во всех точках.
Определение 8. Функция называется замкнутой, если её надграфик замкнут.
Замечание. Пусть $$f$$ — выпуклая собственная функция и $$X = \overline{\R}^n$$. Тогда её замыкание $$\operatorname{cl} f$$ также является собственной функцией.
Полунепрерывность снизу и замкнутость множества Лебега
Определение 9. Множеством Лебега назовем $$\mathcal{L}_a f = \{ x \in X | f(x) \leqslant a \}.$$
Теорема (критерий полунепрерывности снизу). Функция $$f$$ полунепрерывна снизу $$\Leftrightarrow$$, когда для $$\forall a \in \R$$ ее множество Лебега $$\mathcal{L}_a f$$ замкнутое.
Доказательство. Необходимость. Пусть $$f$$ полунепрерывна снизу. Рассмотрим предельную точку $$x_0$$ $$\{x_k\} \subset \mathcal{L}_a f$$. В силу полунепрерывности снизу имеем \begin{gather*} f(x_0) \leqslant \underline{\lim}_{x_k \to x_0} f(x_k) \leqslant a \Rightarrow f(x_0) \leqslant a \Rightarrow x_0 \in \mathcal{L}_a f, \end{gather*} что доказывает замкнутость множества Лебега $$\mathcal{L}_a f$$. Достаточность. Докажем от противного. Предположим $$\exists x_0$$, в которой функция $$f$$ не является полунепрерывной снизу. Тогда $$\{x_k\} \to x_0$$, что \begin{gather*} b = \lim_{x_k \to x_0}f(x_k) < f(x_0). \end{gather*} Выберем число $$a$$ так, что $$b<a<f(x_0)$$. Тогда $$x_k \in \mathcal{L}_a f$$ для всех достаточно больших $$k$$, откуда в силу замкнутости $$\mathcal{L}_a f$$ имеем $$x_0 \in \mathcal{L}_a f$$. Но по построению $$f(x_0)>a$$. Полученное противоречие завершает рассуждения. $$\blacksquare$$
Замкнутость
Теорема (критерий замкнутости). Для замкнутости функции необходимо и достаточно, чтобы она была полунепрерывна снизу.
Доказательство. Необходимость. Пусть функция $$f$$ замкнута. Рассмотрим множество Лебега $$\mathcal{L}_a f$$ и лежащую в нем последовательность точек $$\{x_i\}$$, которая сходится к точке $$x_0$$. Тогда \begin{gather*} f(x_i) a \Rightarrow (x_i, a) \in \operatorname{epi} f, \; (x_i, a) \to (x_0, a). \end{gather*} Из определения замкнутости $$f$$ следует, что $$(x_0,a) \in \operatorname{epi} f \Rightarrow f(x_0) \leqslant a \Rightarrow x_0 \in \mathcal{L}_a f$$. Таким образом, доказано, что все множества Лебега функции $$f$$ замкнуты, откуда вытекает, что она полунепрерывна снизу. Достаточность. Пусть функция $$f$$ полунепрерывна снизу. Рассмотрим последовательность точек $$(x_i, a_i) \in \operatorname{epi} f$$, и пусть $$(x_i, a_i) \to (x_0, a_0)$$, $$i \to \infty$$. Для доказательства замкнутости функции $$f$$ нужно показать, что $$(x_0, a_0) \in \operatorname{epi} f$$. Докажем от противного, т.е. что $$(x_, a_0) \not \in \operatorname{epi} f$$. Тогда $$f(x_0)>a_0$$.
Выберем число γ такое, что $$a_0 < γ< f(x_0)$$. Тогда $$x_0 \not\in \mathcal{L}_γ f$$ и, значит, $$\existsε>0$$ такое, что $$O(x_0, ε)\cap\mathcal{L}_γ f = \varnothing$$, поскольку множества Лебега полунепрерывной снизу функции замкнуты. Поэтому для всех достаточно больших $$i$$ имеем $$x_i \not\in \mathcal{L}_γ f$$, откуда $$f(x_i)>γ$$. Поскольку $$γ>a_0$$, неравенство $$f(x_i)>a_i$$ справедливо для всех достаточно больших $$i$$, а это противоречит тому, что $$(x_0, a_0) \in \operatorname{epi} f$$. $$\blacksquare$$
Замечание. Мы показали, что следующие 3 свойства функции равносильны:
1. полунепрепрерывность снизу,
2. замкнутость всех её множеств Лебега,
3. замкнутость самой функции.
Полунепрерывность сверху
Определение 10. Множество $$M$$ будем называть симплектическим, если его можно представить в виде объединения конечного числа симплексов ($$n$$-мерных обобщений треугольника).
Определение 11. Пусть система векторов $$x_i \in \R^n, \; i = \overline{0, n}$$, аффинно независима, тогда любой вектор $$x \in \R^n$$ можно представить в виде $$x = \sum_{i=0}^n \alpha^ix_i, \; \sum_{i=0}^n \alpha^i = 1$$, причем это представление единственно. Числа $$\alpha^0,.. \alpha^n$$ называются барицентрическими координатами точки $$x$$ относительно системы $$x_0,...,x_n$$.
Пусть $$L=\{\alpha = (\alpha^0,.. \alpha^n) \in \R^{n+1}: \sum_{i=0}^n \alpha^i = 1\}$$ — линейное многообразие. Определим отображение $$\alpha: \R^n \to L$$, где $$\alpha(x)=(\alpha^0,.. \alpha^n)$$ — барицентрические координаты точки $$x_i \in \R^n$$ относительно аффинно независимой системы $$x_0,...,x_n$$.
Теорема. Отображение $$\alpha(\cdot)$$ непрерывное.
Теорема о полунепрерывности сверху. Пусть $$f: \R^n \to \overline{\R}$$ — выпуклая функция и $$M \subset \operatorname{dom} f$$ — симплектическое множество. Тогда сужение $$f$$ на $$M$$ полунепрерывно сверху. То есть, если последовательность $$\{x+i\}$$ лежит во множестве $$M$$ и сходится к точке $$x_0$$, то верхний предел $$f(x_i)$$ не превышает $$f(x_0)$$.
Доказательство. Достаточно рассмотреть только случай, когда само $$M$$ является $$n$$-мерным симплексом. Возьмем точку $$x_0 \in M$$ и докажем, что сужение $$f$$ полунепрерывно сверху в этой точке.
Осуществим барицентрическое подразделение (триангуляцию) симплекса $$M$$ следующим образом. Возьмем какую-нибудь $$(n-1)$$-мерную грань $$Γ_i$$ симплекса $$M$$ (т.е. выпуклую оболочку его $$n$$ вершин) и положим $$M_i = \operatorname{conv}(Γ_i \cup \{x_0\})$$. Таким образом, исходный симплекс представим в виде объединения $$(n+1)$$ симплексов $$M_i$$, у каждого из которых $$x_0$$ является вершиной, и нам достаточно доказать, что $$f$$ полунепрерывна сверху на $$\forall Mi$$.
Не теряя общности считаем, что исходный симплекс $$M = \operatorname{conv}\{x_0,...,x_n\}$$. Для удобства $$x_0 = 0$$.
Произвольная точка $$x \in M$$ $$x = \sum_{i=0}^n \alpha^i(x)x_i$$, где $$\alpha(x) = (\alpha^0(x), ..., \alpha^n(x)))$$ — барицентрические координаты точки $$x$$. По теореме 1 отображение $$\alpha$$ непрерывно. Поэтому при $$x \to 0$$ имеет место $$\alpha^0(x) \to 1, \; \alpha^i(x) \to 0 \; i = 1,...,n$$. В силу выпуклости функции $$f$$ имеем
\begin{gather*} f(x_i) = f \bigl(\sum_{i=0}^n \alpha^i(x)x_i\bigr) \leqslant \sum_{i=0}^n \alpha^i(x)f(x_i) = \alpha^0(x)f(0) + \sum_{i=1}^n \alpha^i(x)f(x_i), \end{gather*} где, с учетом принятого соглашения, для тех номеров $$i$$, для которых $$\alpha^i(x) = 0, \; f(x_i) = -\infty$$, мы полагаем $$\alpha^i(x)f(x_i)=0$$. Из полученного неравенства заключаем, что верхний предел функции $$f$$ при $$x \to 0, \; x \in M$$ не превышает $$f(0)$$, что завершает доказательство полунепрерывности сверху сужения $$f$$ на $$M$$ в точке $$x_0$$. $$\blacksquare$$
Непрерывность в окрестности точки
Теорема о полунепрерывности в окрестности точки. Пусть выпуклая собственная функция $$f: X \to \overline{\R}$$ ограничена сверху в некоторой окрестности заданной точки $$x_0$$. Тогда $$f$$ непрерывна в этой окрестности точки $$x_0$$.
Доказательство. Не ограничивая общности, считаем $$f(0) = 0$$, $$x_0$$. Выберем числа $$c>0$$ и $$\delta > 0$$ так, что $$f(x) \leq x$$ для $$\forall x \in Q = Q_{\delta}$$. Очевидно, $$Q=-Q$$.
Достаточно доказать, что для $$\forall \varepsilon > 0$$ имеет место $$|f(x)|\leq \varepsilon$$ для $$\forall x \in V_{\varepsilon} = \frac{\varepsilon}{c}Q$$. Зафиксируем произвольное $$\varepsilon \in (0,c)$$ и положим $$V = V_{\varepsilon}$$. Очевидно, $$V = -V$$. В силу выпуклости $$f$$ имеем \begin{gather} x = \frac{\varepsilon}{c}\frac{c}{\varepsilon}x + \left(1-\frac{\varepsilon}{c}\right)0 \in V, \end{gather} \begin{gather} f(x) \leq \frac{\varepsilon}{c}f\left(\frac{c}{\varepsilon}x\right) + \left(1 - \frac{\varepsilon}{c}\right)f(0) \end{gather} \begin{gather} f(x) \leq \frac{\varepsilon}{c}f\left(\frac{c}{\varepsilon}x\right) \leq \frac{\varepsilon}{c} c \Longrightarrow f(x) \leq \varepsilon. \end{gather} Далее: \begin{gather} x \in V = -V = -\frac{\varepsilon}{c}Q \Longrightarrow \left(-x\frac{c}{\varepsilon} \right) \in Q, \end{gather} \begin{gather} 0 = \frac{1}{1+\varepsilon/c}x + \frac{\varepsilon/c}{1+\varepsilon/c}\left(-x\frac{c}{\varepsilon} \right). \end{gather} Отсюда в силу выпуклости функции $$f$$ получаем \begin{gather} 0 = f(0) \ leq \frac{1}{1+\varepsilon/c}f(x) + \frac{\varepsilon/c}{1+\varepsilon/c}f\left(-x\frac{c}{\varepsilon} \right) \leq \frac{1}{1+\varepsilon/c}f(x) + \frac{\varepsilon}{1+\varepsilon/c} \Longrightarrow f(x) \geq \varepsilon. \end{gather} $$\blacksquare$$
Следствие (липшицевость в окрестности). Пусть для выпуклой собственной функции $$f: X \to \overline{\R}$$ и точки $$x_0 \in X$$ $$\exists c > 0$$, $$\delta >0$$, что $$f(x) \leqslant c$$ $$\forall x \in O(x_0, 2\delta)$$. Тогда на множестве $$O(x_0, 2\delta)$$ функция $$f$$ удовлетворяет условию Липшица с константой $$c$$:
окрестности точки $$x_0 \in X$$, то
\begin{gather}
\mid f(x_2) - f(x_1)\mid \leqslant c \mid \mid x_2 - x_1 \mid \mid \; \forall x_1, x_2 \in O(x_0, \delta).
\end{gather}
Следствие. Пусть выпуклая собственная функция $$f: X \to \overline{\R}$$ ограничена сверху на некотором непустом открытом множестве. Тогда она непрерывна на множестве $$\operatorname{int}(\operatorname{dom f}) \not = \varnothing$$.
$$\text{int A} $$— внутренность множества$$A $$ множество всех внутренних точек множества $$A$$.
Теорема о липшицевости на выпуклом компакте
Лемма. Пусть $$f$$ выпукла, $$S$$ — выпуклый компакт, $$S \subset \operatorname{int}\operatorname{dom f}$$. Тогда $$\exists \varepsilon > 0$$ т.ч. \begin{gather} \varepsilon B + S \subset \operatorname{int}\operatorname{dom f}, \end{gather} где $$B$$ — единичный шар в $$X = R^n$$.
Доказательство. От противного. Пусть $$\exists \{x_i\}:$$ $$x_i \in (B/i + S) \notin \operatorname{int}\operatorname{dom f}.$$ Так как $$ (B/i + S)$$ — последовательность вложенных компактов, то последовательность $$\{x_i\}$$ ограничена. Переходя к подпоследовательности считаем $$x_i \rightarrow x_0$$. Очевидно $$x_0 \in S$$, $$x_0 \notin \operatorname{int}\operatorname{dom f}.$$ Противоречие с условием $$S \subset \operatorname{int}(\operatorname{dom f})$$. Значит, такой $$\varepsilon$$ существует. $$\blacksquare$$
Теорема. Пусть $$f: \R^n \to \overline{\R}$$ — собственная выпуклая функция, $$S$$ - выпуклый компакт и $$S \subset \operatorname{int}(\operatorname{dom f})$$. Тогда на множестве $$S$$ функция $$f$$ удовлетворяет условию Липшица.
Доказательство. 1. Обозначим $$m = \min_{x \in B + S} f(x)$$, $$M = \max_{x \in B + S} f(x)$$. Эти величины существуют в силу $$f \in C(\operatorname{dom f})$$. $$\blacksquare$$
2. $$\forall x, y \in S$$ положим $$z = y + \varepsilon(y-x)/|y-x|$$. Значит, $$z \in S + \varepsilon B$$. Выражая $$y$$, получим $$y = (1-\lambda)x + \lambda z$$, где $$\lambda = |y-x|/(|y-x| + \varepsilon) = 1 - \varepsilon/(|y-x| + \varepsilon) < 1.$$
3. В силу выпуклости $$f$$: \begin{gather} f(y) \leqslant (1-\lambda)f(x) + \lambda f(z) = f(x) + \lambda (f(z) - f(x)) \\ f(y) - f(x) \leqslant \lambda(f(z) - f(x)) = \frac{|y-x|(f(z)-f(x))}{|y-x|+\varepsilon} \leqslant \frac{|y-x|(M-m)}{|y-x|+\varepsilon} \leqslant \frac{M-m}{\varepsilon}|y-x| = C|y-x|, \end{gather} Где $$C = (M-m)\varepsilon$$ — константа Липшица. Таким образом, в силу произвольности точек $$x, y \in S$$ выражение \begin{gather} |f(x) - f(y)| \leqslant C|x-y| \end{gather} выполняется всегда. $$\blacksquare$$
Список литературы
1. Арутюнов А. В. "Лекции по выпуклому и многозначному анализу", М.: ФИЗМАТЛИТ, 2004;
2. Фихтенгольц Г. М. "Курс дифференциального и интегрального исчисления." 8-е изд. М.; СПб., 2001;
3. Ильин В. А., Позняк Э. Г. "Основы математического анализа." 6-е изд. М., 2001. Т. 1.